第21話  空気抵抗のみを受ける撥弦

この記事を読む助けになる数学の記事
・数値計算： 1話、 2話、 3話、 4話、 5話、 6話、 7話、 13話、 22話、 24話、 25話、 26話、 28話

―説明書―
　空気抵抗のみを考慮した撥弦による弦の振動のシミュレータです。
・表示画面下の設定項目について
　\( c \) ：位相速度
　\( p \) ：減衰係数
　\( L \) ：弦の長さ

画面上の弦（黒線）をドラッグして弦を引っ張り、ドロップすると弦を弾きます。 弦を弾くと音が鳴ります（最長5秒間）。「一時停止」ボタンを押すとシミュレーションを一時停止します（音は止まりません）。 もう一度ボタンを押すと、一時停止したところからシミュレーションを開始します。

　弦を指やピックで弾いて音を鳴らす楽器を撥弦楽器と呼びます。 代表的な撥弦楽器としては、ギターやハープ、琴などが挙げられます。 一般的に、弦の振動を物理的なモデルにより解析する場合、空気抵抗に加えて弦の弾性や音響放射などを考慮したモデルが用いられます。 今回は、簡単のため空気抵抗による振動の減衰のみを考慮した次のモデルを用いました。

このモデルは1次元消散型波動方程式の形になっています。 位相速度 \( c \) は弦の張力 \( \tau \) と線密度 \( \rho \) に関係しており、 \[ c = \sqrt{\frac{\tau}{\rho}} \] が成り立ちます。以下では弦の長さを \( L \) とし、両端固定の条件で \( (1) \) をフーリエ級数を用いて解いていきます。 ただ、証明が長いので、先に最終的な結果を示しておきます。

　証明に入ります。まずは、\( (1) \) の解 \( u \left( x,t \right) \) が \( x \) のみを独立変数とする関数 \( X(x) \) と \( t \) のみを独立変数とする関数 \( T(t) \) との積で表されると仮定します。 \[ u \left( x,t \right) = X(x)T(t) \ \ \ \ldots (2) \] \( (2) \) を \( (1) \) に代入すると次式を得ます。 \[ X(x)T^{(2)}(t) = c^2 X^{(2)}(x)T(t) - p X(x)T'(t) \] 左辺に \( t \) の関数、右辺に \( x \) の関数が来るように変形すると次式を得ます。 \[ \frac{T^{(2)}(t) + pT'(t)}{c^2 T} = \frac{X^{(2)}(x)}{X(x)} \] この式は左辺と右辺で変数が異なるため、常に等号が成立するなら、\( q \) を定数として、 \[ \frac{T^{(2)}(t) + pT'(t)}{c^2 T} = \frac{X^{(2)}(x)}{X(x)} = q\] が成り立ちます。そこで、この式から次の2つの常微分方程式が導かれます。 \[ X^{(2)}(x) -qX(x) = 0 \ \ \ \ldots (3)\] \[ T^{(2)}(t) + pT'(t) -qc^2T(t) = 0 \ \ \ \ldots (4)\] 2つの常微分方程式を解くために、まずは境界条件の式を導きます。 弦は両端で固定されているため、 \[ u \left( 0,t \right) = u \left( L,t \right) = 0\] とします。すると、\( (2) \) 式より、 \[ X(0)T(t) = X(L)T(t) = 0\] となりますが、\( T(t) = 0 \) の場合、弦が振動しないため、求めたい条件は、 \[ X(0) = X(L) = 0 \ \ \ \ldots (5) \] になります。 \( (5) \) 式を用いて、まずは \( (3) \) 式を解きます。 \( (3) \) 式は定数係数2階同次線形常微分方程式であり、その解は \( q \) の条件によって次の 3 パターンに分かれます。

[1] \( q \gt 0 \) のとき。 \( (3) \) 式の一般解は、 \[ \begin{align} X \left( x \right) = A e^{\sqrt{q}x} + B e^{-\sqrt{q}x} \end{align}\] という形になります。\( (5) \) 式を満たすためには、次の二つの式 \[ \begin{align} A + B &= 0 \\\\ A e^{\sqrt{q}L} + B e^{-\sqrt{q}L} &= 0 \end{align}\] が共に成り立つ必要があります。上の式から、\( B = -A \) なので、これを下の式に代入すると \[ \begin{align} A e^{\sqrt{q}L} - A e^{-\sqrt{q}L} &= 0 \\\\ A \left( e^{\sqrt{q}L} - e^{-\sqrt{q}L} \right) &= 0 \end{align}\] となります。かっこの中は 0 とならないため、\( A = 0 \) となり、これから \( B = 0 \) もわかります。 よって、境界条件を満たす \( (3) \) 式の解は結局 \( X \left( x \right) =0 \) となりますが、これは弦がまったく振動しないということなので、考えません。

[2] \( q = 0 \) のとき。 \( (3) \) 式の一般解は、 \[ \begin{align} X \left( x \right) = A x + B \end{align}\] という形になります。\( (5) \) 式を満たすためには、 \[ \begin{align} A = B = 0 \end{align}\] が成り立つ必要があるため、境界条件を満たす \( (3) \) 式の解は結局 \( X \left( x \right) =0 \) となり、[1] 同様これは考えません。

[3] \( q \lt 0 \) のとき。 \( (3) \) 式の一般解は、 \[ \begin{align} X \left( x \right) = A \cos \left( \sqrt{-q} x \right) + B \sin \left( \sqrt{-q} x \right) \end{align}\] という形になります。\( (5) \) 式を満たすためには、 \[ \begin{align} A \cos \left( \sqrt{-q} \cdot 0 \right) + B \sin \left( \sqrt{-q} \cdot 0 \right) = 0 \\\\ A \cos \left( \sqrt{-q} L \right) + B \sin \left( \sqrt{-q} L \right) = 0 \end{align}\] が共に成り立つ必要があります。上の式から、\( A = 0 \) となるため、下の式は \[ \begin{align} B \sin \left( \sqrt{-q} L \right) = 0 \end{align}\] となります。ここで、\( B = 0 \) としてしまうと、[1] と [2] 同様 \( X \left( x \right) =0 \) となってしまうので、 \[ \begin{align} \sin \left( \sqrt{-q} L \right) = 0 \end{align}\] である必要があります。よって、これを満たす定数 \( q \) の値を \( q_n \) とすれば、 \[ \begin{align} q_n = - \left( \frac{n \pi}{L} \right) ^2 \ \ \ \left( n = 1,2, \ldots \right) \ \ \ \ldots (6) \end{align}\] となります。したがって、境界条件を満たす \( (3) \) 式の解は、\( B_n \) を任意の定数として、 \[ \begin{align} X \left( x \right) &= X_n \left( x \right) \\\\ &= B_n \sin \left( \sqrt{-q_n} x \right) \\\\ &= B_n \sin \frac{n \pi}{L} x \ \ \ \left( n = 1,2, \ldots \right) \ \ \ \ldots (7) \end{align}\] となります。

　次は \( (4) \) 式について考えます。\( (6) \) 式の条件から、\( (4) \) 式を次のように書き換えます。 \[ \begin{align} T^{(2)}(t) + pT'(t) + \omega _n ^2 T(t) = 0 \ \ \ \ldots (4)' \\\\ \omega _n = \frac{cn \pi}{L} \ \ \ \left( n = 1,2, \ldots \right) \ \ \ \ldots (8) \end{align}\] \( (4)' \) 式は定数係数2階同次線形常微分方程式であり、特性方程式は \[ \begin{align} \lambda^2 + p \lambda + \omega _n ^2 = 0 \end{align}\] です。この特性方程式の解は、 \[ \begin{align} \lambda = \frac{-p \pm \sqrt{p^2 - 4 \omega _n ^2}}{2} \end{align}\] であるため、\( (4)' \) 式は \( p^2 -4 \omega _n ^2 \) の値に応じて 3 種類の一般解を持ちます。 ただし、\( p^2 -4 \omega _n ^2 \geq 0 \) の場合の解は実数値を変数とする指数関数の和によって表されるため、弦の振動を表現するには適切ではありません。 そこで、以降は \( p^2 -4 \omega _n ^2 \lt 0 \) の場合に限って考察を進めます。 すると、\( (4)' \) 式の一般解は \( \alpha _n \) 、\( \beta _n \) を任意の定数として、次式で与えられます。 \[ \begin{align} T \left( t \right) &= T_n \left( t \right) \\\\ &= e^{-\frac{p}{2} t} \left( \alpha _n \cos \frac{\sqrt{4 \omega _n ^2 - p^2}}{2} t + \beta _n \sin \frac{\sqrt{4 \omega _n ^2 - p^2}}{2} t \right) \\\\ &= e^{-\frac{p}{2} t} \left( \alpha _n \cos \Omega _n t + \beta _n \sin \Omega _n t \right) \ \ \ \ldots (9) \\\\ \Omega _n &= \frac{\sqrt{4 \omega _n ^2 - p^2}}{2} \ \ \ \left( n = 1,2, \ldots \right) \ \ \ \ldots (10) \end{align}\]

　\( (2) \) 式、\( (7) \) 式、\( (9) \) 式より、次式で与えられる \( u_n \left( x,t \right) \) は境界条件を満たす \( (1) \) 式の解になります。 \[ \begin{align} u_n \left( x,t \right) &= X_n (x) T_n (t) \\\\ &= e^{-\frac{p}{2} t} \left( a _n \cos \Omega _n t + b _n \sin \Omega _n t \right) \sin \frac{n \pi}{L} x \ \ \ \left( n = 1,2, \ldots \right) \ \ \ \ldots (11) \end{align}\] \( (11) \) 式で、\( a_n = \alpha _ n B_n \) 、\( b_n = \beta _n B_n \) と任意の定数を置きなおしました。

　\( (1) \) 式は線形同次微分方程式なので、重ね合わせの原理から \( u_n \left( x,t \right) \) を複数個足し合わせたものも \( (1) \) 式の解になります。よって、次式は \( (1) \) 式の解になります。 \[ \begin{align} u \left( x,t \right) &= \sum _{n=1} ^{\infty} u_n \left( x,t \right) \\\\ &= e^{-\frac{p}{2} t} \sum _{n=1} ^{\infty} \left( a _n \cos \Omega _n t + b _n \sin \Omega _n t \right) \sin \frac{n \pi}{L}x \ \ \ \ldots (12) \end{align}\] あとは、\( (12) \) 式が初期条件を満たすように任意の定数 \( a_n \) と \( b_n \) を定める必要があります。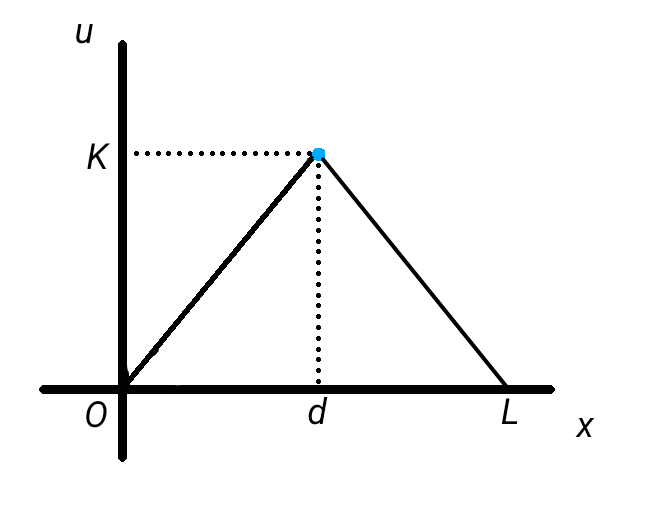 初期条件については、弦を位置 \( d \) で高さ \( K \) だけ引っ張った状態を想定し次で与えます。 \[ u \left( x,0 \right) = \begin{cases} \displaystyle \frac{K}{d} x & \left( 0 \lt x \leq d \right) \\[1em] \displaystyle \frac{K \left( L - x \right) }{L - d} & \left( d \lt x \lt L \right) \end{cases} \ \ \ \ldots (13) \] \[ \frac{\partial u \left( x,0 \right)}{\partial t} = 0 \ \ \ \ldots (14)\]

　次に、\( (12) \) 式に \( t=0 \) を代入して、\( u \left( x,0 \right) \) を別の形で表します。 \[ \begin{align} u \left( x,0 \right) &= e^{0} \sum _{n=1} ^{\infty} \left( a _n \cos 0 + b _n \sin 0 \right) \sin \frac{n \pi}{L}x \\\\ &= \sum _{n=1} ^{\infty} a _n \sin \frac{n \pi}{L}x \ \ \ \ldots (15) \end{align}\] \( (13) \) 式と \( (15) \) 式から、\( u \left( x,0 \right) \) は \( (13) \) 式右辺の関数の半区間でのフーリエ正弦級数であるとわかります。よって、 \[ \begin{align} a_n &= \frac{2}{L} \int _0 ^d \frac{K}{d}x \sin \frac{n \pi}{L}x dx + \frac{2}{L} \int _d ^L \frac{K \left( L - x \right) }{L - d} \sin \frac{n \pi}{L}x dx \\\\ &= \frac{2K}{L} \left\{ \frac{1}{d} \int _0 ^d x \sin \frac{n \pi}{L}x dx + \frac{1}{L-a} \int _d ^L \left( L - x \right) \sin \frac{n \pi}{L}x dx \right\} \end{align}\] 先に、カッコ内の積分を計算しておきます。 \[ \begin{align} \int _0 ^d x \sin \frac{n \pi}{L}x dx &= \int _0 ^d x \left( - \frac{L}{n \pi} \cos \frac{n \pi}{L}x \right)' dx \\\\ &= \left[ - \frac{L}{n \pi} x \cos \frac{n \pi}{L}x \right] _0 ^d + \int _0 ^d \frac{L}{n \pi} \cos \frac{n \pi}{L}x \\\\ &= - \frac{Ld}{n \pi} \cos \frac{n \pi d }{L} + \left[ \frac{L^2}{n^2 \pi ^2} \sin \frac{n \pi}{L}x \right] _0 ^d \\\\ &= - \frac{Ld}{n \pi} \cos \frac{n \pi d }{L} + \frac{L^2}{n^2 \pi ^2} \sin \frac{n \pi d}{L} \\\\ &= \frac{L}{n \pi} \left( -d \cos \frac{n \pi d }{L} + \frac{L}{n \pi} \sin \frac{n \pi d}{L} \right) \end{align}\]
\[ \begin{align} \int _d ^L \left( L - x \right) \sin \frac{n \pi}{L}x dx &= L \int _d ^L \sin \frac{n \pi}{L}x dx - \int _d ^L x \sin \frac{n \pi}{L}x dx \\\\ &= L \left[ - \frac{L}{n \pi} \cos \frac{n \pi}{L}x \right] _d ^L - \left\{ \left[ - \frac{L}{n \pi} x \cos \frac{n \pi}{L}x \right] _d ^L + \frac{L^2}{n^2 \pi ^2} \left[ \sin \frac{n \pi}{L}x \right] _d ^L \right\} \\\\ &= - \frac{L^2}{n \pi } \left( \cos n \pi - \cos \frac{n \pi d}{L} \right) - \left\{ - \frac{L}{n \pi} \left( L \cos n \pi - d \cos \frac{n \pi d}{L} \right) - \frac{L^2}{n^2 \pi ^2} \sin \frac{n \pi d}{L} \right\} \\\\ &= \frac{L^2}{n \pi } \cos \frac{n \pi d}{L} - \frac{Ld}{n \pi } \cos \frac{n \pi d}{L} + \frac{L^2}{n^2 \pi ^2} \sin \frac{n \pi d}{L} \\\\ &= \frac{L}{n \pi } \left( L \cos \frac{n \pi d}{L} - d \cos \frac{n \pi d}{L} + \frac{L}{n \pi } \sin \frac{n \pi d}{L} \right) \end{align}\] よって、 \[ \begin{align} a_n &= \frac{2K}{L} \left\{ \frac{1}{d} \frac{L}{n \pi} \left( -d \cos \frac{n \pi d }{L} + \frac{L}{n \pi} \sin \frac{n \pi d}{L} \right) + \frac{1}{L-a} \frac{L}{n \pi } \left( L \cos \frac{n \pi d}{L} - d \cos \frac{n \pi d}{L} + \frac{L}{n \pi } \sin \frac{n \pi d}{L} \right) \right\} \\\\ &= \frac{2K}{n \pi} \left\{ - \cos \frac{n \pi d }{L} + \frac{L}{n \pi d} \sin \frac{n \pi d}{L} + \cos \frac{n \pi d}{L} + \frac{L}{n \pi \left( L - d \right)} \sin \frac{n \pi d}{L} \right\} \\\\ &= \frac{2KL}{n^2 \pi ^2} \left\{ \frac{1}{d} \sin \frac{n \pi d}{L} + \frac{1}{\left( L - d \right)} \sin \frac{n \pi d}{L} \right\} \\\\ &= \frac{2KL^2}{n^2 \pi ^2 d \left( L - d \right)} \sin \frac{n \pi d}{L} \end{align}\]

　あとは、\( b_n \) を求めます。初期条件 \( (14) \) 式を使うために、\( u \left( x,t \right) \) を \( t \) で偏微分します。 \[ \begin{align} \frac{\partial u \left( x,t \right)}{\partial t} = - & \frac{p}{2} e^{-\frac{p}{2} t} \sum _{n=1} ^{\infty} \left( a _n \cos \Omega _n t + b _n \sin \Omega _n t \right) \sin \frac{n \pi}{L}x \\\\ & + e^{-\frac{p}{2} t} \sum _{n=1} ^{\infty} \left( -a _n \Omega _n \sin \Omega _n t + b _n \Omega _n \cos \Omega _n t \right) \sin \frac{n \pi}{L}x \end{align}\] この式に \( t =0 \) を代入すると、初期条件 \( (14) \) 式より \[ \begin{align} \frac{\partial u \left( x,0 \right)}{\partial t} &= - \frac{p}{2} \sum _{n=1} ^{\infty} a _n \sin \frac{n \pi}{L}x + \sum _{n=1} ^{\infty} b _n \Omega _n \sin \frac{n \pi}{L}x \\\\ &= \sum _{n=1} ^{\infty} \left( - \frac{p}{2} a_n + b_n \Omega _n \right) \sin \frac{n \pi}{L}x = 0 \end{align}\] この式が \( x \) の値によらず成り立つことから、 \[ \begin{align} - \frac{p}{2} a_n + b_n \Omega _n &= 0 \\\\ b_n &= \frac{p}{2 \Omega _n} a_n \end{align}\] 　以上で、題意を示すことができました。