目次
・単振り子
・面積速度一定の法則
カヤ
ゆーらゆーら、はい、回ったー。
ナユミ
なにやってるの？
カヤ
ブランコのシミュレーション。
―説明書―
ブランコのシミュレータです。
「位置」スライダーでブランコを揺らす開始点を決めます。 「開始/停止」ボタンを押すとシミュレーションが始まります。 シミュレーション中に「上昇/下降」ボタンを押すと、青の●で描かれた重りの位置が変わり、ブランコを漕ぐことができます。
ブランコのシミュレータです。
「位置」スライダーでブランコを揺らす開始点を決めます。 「開始/停止」ボタンを押すとシミュレーションが始まります。 シミュレーション中に「上昇/下降」ボタンを押すと、青の●で描かれた重りの位置が変わり、ブランコを漕ぐことができます。
ナユミ
ブランコなんて久しく乗ってないけど、タイミングよく漕ぐとどんどん大きく揺れて面白いわね。
カヤ
だな。漕ぎ方によっては揺れを小さくもできるぞ。こんな感じで。
ナユミ
小さくなったわ。うまいことできてるけど、これもニュートンの運動方程式？
カヤ
うん、そうだな。単振り子の運動方程式を使っている。解説しよう。
単振り子
ブランコの立ち漕ぎを表すモデルの一つとして、単振り子の運動方程式を用いるものがあります。
\[ 単振り子の運動方程式\]
\[ \frac{d^2 \theta}{dt^2} = - \frac{g}{l} \sin \theta\]
\( \theta \) ：角度、\( t \) ：時刻、\( g \) ：重力加速度、\( l \) ：棒の長さ
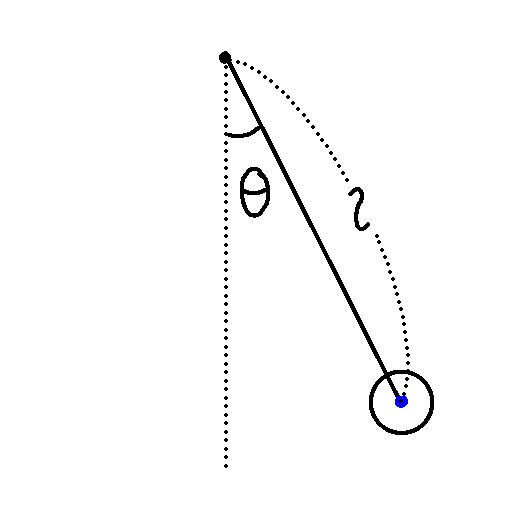
この運動方程式の導出はここではしませんが、注意点としてこの式は角度 \( \theta \) についての式であるということを挙げておきます。
2次元運動は通常 \( x \) 軸方向と \( y \) 軸方向に分けて運動方程式を立てるのですが、単振り子の運動の場合、角度 \( \theta \) と棒の長さ \( l \) が決まれば、棒の固定点を原点として、
\[ \begin{align}
x &= l \cos \left( \theta - \frac{\pi}{2} \right) \\\\
y &= l \sin \left( \theta - \frac{\pi}{2} \right)
\end{align}\]
の関係により \( x \) と \( y \) が定まるため、上の運動方程式で単振り子の運動を表すことができています。
ブランコの話に戻ると、立ち漕ぎの動作は単振り子の質量の中心（上図の青色の点）が上下に動くことと見ることができます。 これは、単振り子の運動方程式にある棒の長さ \( l \) が変動することと同じと言えます。 ただし、単純に棒の長さ \( l \) を増減させながら運動方程式をルンゲ=クッタ法などで解くと、次の面積速度一定の法則が成り立ちません。
ブランコの話に戻ると、立ち漕ぎの動作は単振り子の質量の中心（上図の青色の点）が上下に動くことと見ることができます。 これは、単振り子の運動方程式にある棒の長さ \( l \) が変動することと同じと言えます。 ただし、単純に棒の長さ \( l \) を増減させながら運動方程式をルンゲ=クッタ法などで解くと、次の面積速度一定の法則が成り立ちません。
面積速度一定の法則
\[ 面積速度一定の法則\]
変化前の棒の長さを \( l_1 \) 、変化後の棒の長さを \( l_2 \) とする。
また、角速度 \( \omega = d \theta / dt \) という変数を導入し、
変化前の角速度を \( \omega _1 \) 、変化後の角速度を \( \omega _2 \) とする。このとき、面積速度一定の法則より次式が成り立つ。
\[ l_1 ^2 \omega _1 = l_2 ^2 \omega _2 \]
面積速度一定の法則を単振り子の運動方程式に反映させるために、上の式を次のように変形していきます。
時間区間 \( \Delta t \) における棒の長さの変化を考える。面積速度一定の法則より、
\[ \begin{align}
\ \ \ \ l \left( t + \Delta t \right) ^2 \omega \left( t + \Delta t\right) &= l \left( t \right) ^2 \omega \left( t \right) \\\\
\omega \left( t + \Delta t\right) &= \omega \left( t \right) \frac{l \left( t \right) ^2}{l \left( t + \Delta t \right) ^2} \\\\
\omega \left( t + \Delta t\right) - \omega \left( t \right) &= \omega \left( t \right) \frac{l \left( t \right) ^2 - l \left( t + \Delta t \right) ^2}{l \left( t + \Delta t \right) ^2} \\\\
\frac{\omega \left( t + \Delta t\right) - \omega \left( t \right)}{\Delta t} &= \frac{\omega \left( t \right)}{l \left( t + \Delta t \right) ^2} \cdot \left\{ l \left( t \right) + l \left( t + \Delta t \right) \right\} \cdot \frac{l \left( t \right) - l \left( t + \Delta t \right)}{\Delta t}
\end{align}\]
\( l \left( t \right) \) が微分可能であれば、両辺 \( \Delta t \to 0 \) の極限をとると、
\[ \begin{align}
\frac{d \omega \left( t \right)}{dt} &= \frac{\omega \left( t \right)}{l \left( t \right) ^2} \cdot 2 l \left( t \right) \cdot \left( - \frac{d l \left( t \right)}{dt} \right) \\\\
&= - \frac{2 \omega \left( t \right)}{l \left( t \right) } \frac{d l \left( t \right)}{dt}
\end{align}\]
\( \omega \left( t \right) = d \theta / dt \) より、
\[ \frac{d ^2 \theta}{dt^2} = - \frac{2}{l \left( t \right) } \frac{d l \left( t \right)}{dt} \frac{d \theta}{dt}\]
最後の式の右辺をみると、\( d l \left( t \right) / dt \) が負のとき、つまり棒の長さが短くなっているときに \( d \theta /dt \) と \( d^2 \theta / dt^2 \) の正負が一致し、逆に棒の長さが長くなっているときは
\( d \theta /dt \) と \( d^2 \theta / dt^2 \) の正負は反転するとわかります。
よって、面積速度一定の法則によれば、ブランコの立ち漕ぎにおいては、立ち上がるときに加速され、しゃがむときに減速されると言えます。
また、最後の式の右辺は角速度 \( d \theta / d t \) に比例するため、角速度の絶対値 \( |d \theta / d t| \) が最大となるブランコの最下点で立ち上がり、
角速度の絶対値 \( |d \theta / d t| \) が0となるブランコの最高点でしゃがむというサイクルを繰り返すと揺れが大きくなっていきます。
先ほどの単振り子の運動方程式に最後の式の右辺を加えることで、ブランコを立ち漕ぎするときの運動方程式を得ます。
先ほどの単振り子の運動方程式に最後の式の右辺を加えることで、ブランコを立ち漕ぎするときの運動方程式を得ます。
\[ ブランコ立ち漕ぎの運動方程式\]
\[ \frac{d^2 \theta}{dt^2} = - \frac{g}{l \left( t \right)} \sin \theta - \frac{2}{l \left( t \right) } \frac{d l \left( t \right)}{dt} \frac{d \theta}{dt}\]
\( l \left( t \right) \) は微分可能な関数であれば何でも構いません。
冒頭のシミュレータでは、青色の●の上昇と下降はいずれも \( \Delta t = 0.2 \) の間に行われ、\( l \) は \( l=1 \) と \( l=1.1 \) を行き来するとしています。
上昇中と上昇後、下降中と下降後の \( l \left( t \right) \) を具体的に式で書くと次のようになります。
上昇あるいは下降が始まる時刻を \( t_0 \) とする。
上昇中 \[ l \left( t \right) = 1 + \frac{1}{2} \left( t - t_0 \right)\] 上昇後 \[ l \left( t \right) = 1.1\] 下降中 \[ l \left( t \right) = 1.1 - \frac{1}{2} \left( t - t_0 \right)\] 下降後 \[ l \left( t \right) = 1\]
上昇中 \[ l \left( t \right) = 1 + \frac{1}{2} \left( t - t_0 \right)\] 上昇後 \[ l \left( t \right) = 1.1\] 下降中 \[ l \left( t \right) = 1.1 - \frac{1}{2} \left( t - t_0 \right)\] 下降後 \[ l \left( t \right) = 1\]
なお、この設定では \( t_0 \) と \( t_0 + 0.2 \) において \( l \left( t \right) \) は極限値が存在せず微分可能ではありません。
そのため、数値計算の際にはこれら2点においては
\[ \frac{d l \left( t \right)}{dt} = \frac{0 \pm \frac{1}{2}}{2} = \pm \frac{1}{4}\]
として計算しています。符号はプラスが上昇時、マイナスが下降時を表しています。
ちなみに、この設定は棒の長さが2mのブランコに身長 179cm の男性が立って乗り、膝を軽く曲げて漕ぐ場合の身体重心の変化を想定しています。
ちなみに、この設定は棒の長さが2mのブランコに身長 179cm の男性が立って乗り、膝を軽く曲げて漕ぐ場合の身体重心の変化を想定しています。
ナユミ
ブランコの漕ぎ方にもやり方があったのね。
カヤ
そうだな。ここでは紹介しなかったが座り漕ぎはもっと難しい話になる。興味がある人は参考の[3]を読んでみるといいかもな。
参考：
[1] Wikipedia 係数励振、https://ja.wikipedia.org/wiki/係数励振、2024年3月18日閲覧
[2] 東大物理'21年前期[1]、https://kgkrkgk.com/phys/tup21f1.htm、2024年3月20日閲覧
[3] Chiaki Hirata, Shun'ichi Kitahara, Yuji Yamamoto, Kazutoshi Gohara, and Michael J. Richardson、Initial phase and frequency modulations of pumping a playground swing、Phys. Rev. E 107, 044203、10 April 2023
前の記事
第19話
2次元波動方程式
2次元波動方程式
次の記事
第20話
反応拡散系
反応拡散系