目次
・角度の定義
・三角関数
・加法定理
・三角関数の合成
・和と積の変換公式
・sinc関数の極限公式
・追記：逆三角関数
カヤ
今回は三角関数について解説していく。まずは、角度の定義から始めていこう。
角度の定義
ナユミ
角度は角度でしょ。 \( 180 ^{\circ} \) とか。
カヤ
日常生活では角度を \( ^{\circ} \) で表すのが一般的だが、数学では弧度法と呼ばれる方法を使って角度を表すんだ。
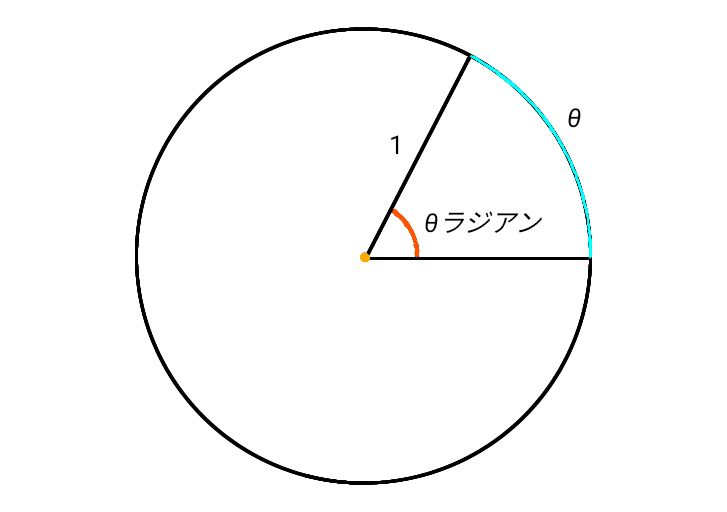
\[ 弧度法\]
半径が \( 1 \) の円において、弧の長さが \( \theta \) のときの中心角を \( \theta \) ラジアンという。
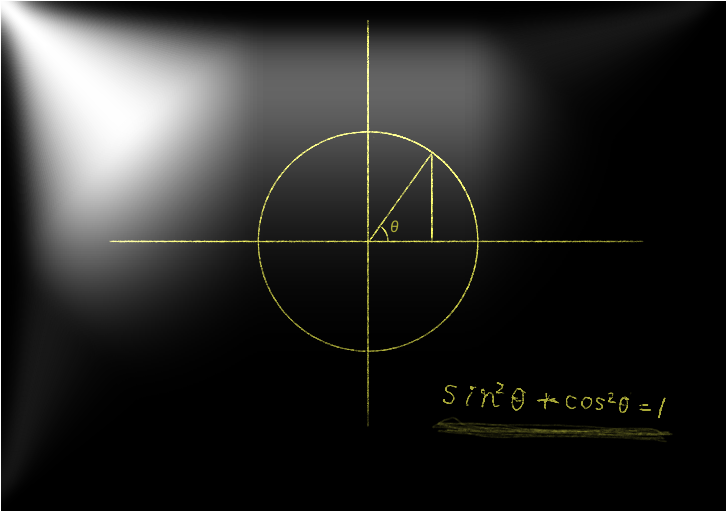
上の図の黄色で塗った丸が円の中心です。そこから少し外側にあるオレンジ色で塗ったところが角度、一番外側の水色で塗ったところが弧です。
弧の長さと角度がどちらも \( \theta \) になっています。角度にはラジアンという単位がついていますが、普通は単位のラジアンは省略されることが多いです。
ラジアンと度 \( ( ^{\circ} ) \) の間には次の関係が成り立ちます。
\[ \pi \ ラジアン \ = 180^{\circ} \]
ここで、\( \pi \) は円周率です。\( (円周の長さ) = (直径) \times (円周率) \) なので、半径が \( 1 \) 、つまり直径が \( 2 \) の円周の長さは \( 2
\pi \) になります。円周の長さに対応する中心角は \( 360 ^{\circ} \) なので、
\[ 2 \pi ラジアン = 360 ^{\circ} \]
になり、これを両辺 \( 2 \) で割ったものが先ほどの関係式になります。
ナユミ
弧度法では弧の長さと角度を結びつけるのね。
カヤ
そういうことだな。じゃあ次は一般角を定義して、角度を実数全体に拡張しよう。
\[ 一般角\]
\( xy \) 平面上に、原点 \( O \) を中心とする半径 \( 1 \) の円を取る。この円を単位円と呼ぶ。点 \( A (1,0) \) を出発点として、点 \( P \)
が単位円の円周上を動くとする。点 \( P \) の動き方に応じて、一般角 \( \theta \) （「シータ」と読む）を次のように定める。
[1] 点 \( P \) が単位円周上を反時計周りに動いたとき、\( \theta = \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \) とする。ただし、\( n \) を任意の自然数として、点 \( P \) が単位円周上を反時計回りに \( n \) 周以上動いたときは、\( \theta = \angle POA + 2n \pi \) とする。
[2] 点 \( P \) が単位円周上を時計周りに動いたとき、\( \theta = - \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \) とする。ただし、\( n \) を任意の自然数として、点 \( P \) が単位円周上を時計回りに \( n \) 周以上動いたときは、\( \theta = - \angle POA - 2n \pi \) とする。
[1] 点 \( P \) が単位円周上を反時計周りに動いたとき、\( \theta = \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \) とする。ただし、\( n \) を任意の自然数として、点 \( P \) が単位円周上を反時計回りに \( n \) 周以上動いたときは、\( \theta = \angle POA + 2n \pi \) とする。
[2] 点 \( P \) が単位円周上を時計周りに動いたとき、\( \theta = - \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \) とする。ただし、\( n \) を任意の自然数として、点 \( P \) が単位円周上を時計回りに \( n \) 周以上動いたときは、\( \theta = - \angle POA - 2n \pi \) とする。
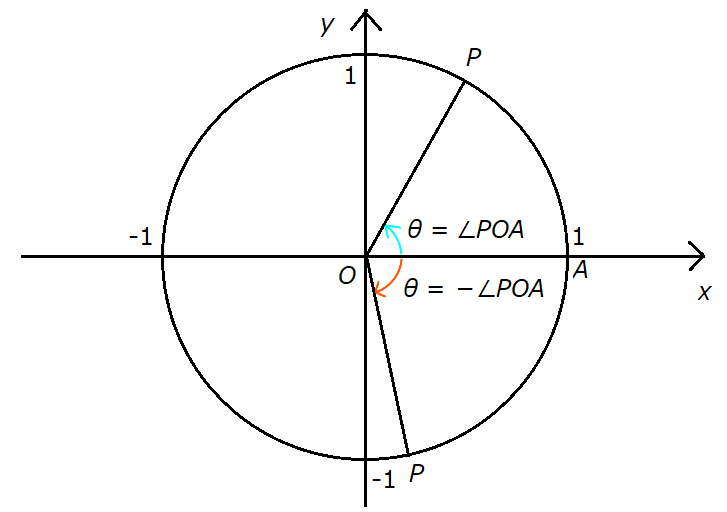
上の図で、時計回りはオレンジの矢印、反時計回りは水色の矢印で表しています。
\( \angle POA \) は角 \( POA \) と読み、これは線分 \( OP \) と線分 \( OA \) のなす角のことです。
なお、線分は両端のあるまっすぐな線のことです。
\( \angle POA \) には線分 \( OP \) と線分 \( OA \) で囲まれてる側と、外側にあるのと二種類ありますが、
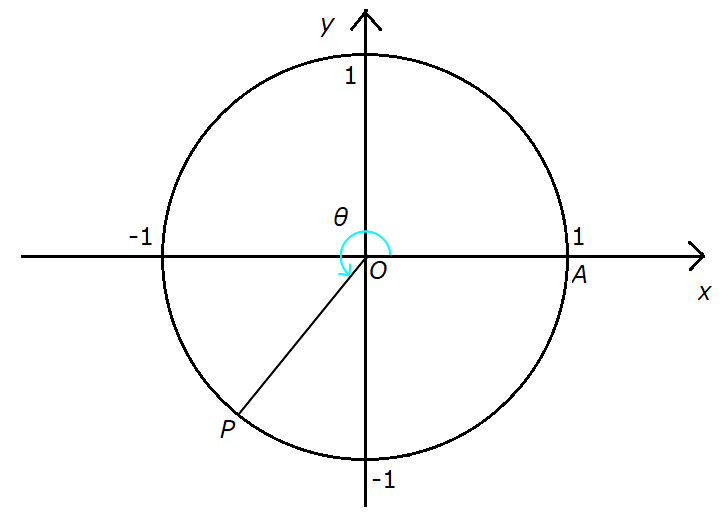
\( 0 \leq \theta \leq \pi \) のときは内側を、\( \pi \lt \theta \lt 2 \pi \)
のときは外側を使って一般角を表します。上の図は内側を使っている場合ですが、外側を使う場合は次の図のようになります。
ナユミ
点 \( P \) がぐるぐる回って一般角になるのね。
カヤ
そうだな。じゃあ、次はいよいよ三角関数に移ろう。
三角関数
ナユミ
”三角”関数って言うぐらいだから、三角形が関係しているのよね？
カヤ
そうだな。定義はこうだ。
\[ 三角関数\]
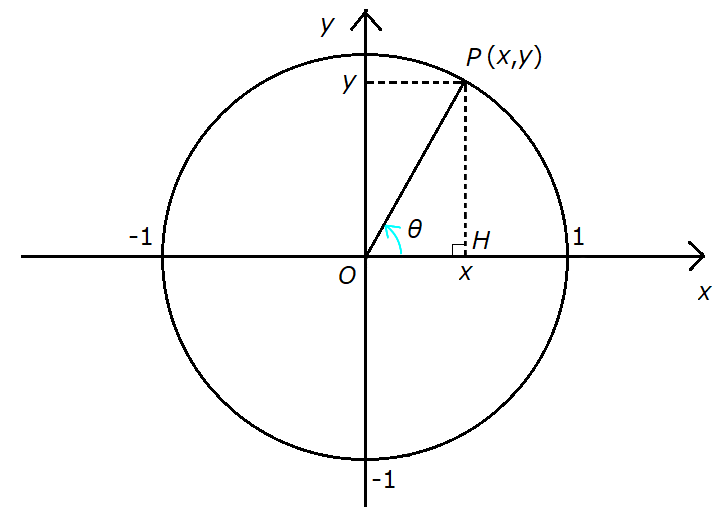
単位円周上に点 \( P (x,y) \) を取り、一般角を \( \theta \) で表す。このとき、次の三つの \( \theta \) の関数を三角関数と呼ぶ。
\[ \sin \theta = y\]
\[ \cos \theta = x\]
\[ \tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{y}{x} \ (x \neq 0) \]
\( \sin \) はサイン、\( \cos \) はコサイン、\( \tan \)
はタンジェントと読みます。また、サインは正弦（せいげん）、コサインは余弦（よげん）、タンジェントは正接（せいせつ）とも呼ばれています。
三角関数の”三角”は上図の三角形 \( POH \) に由来します。
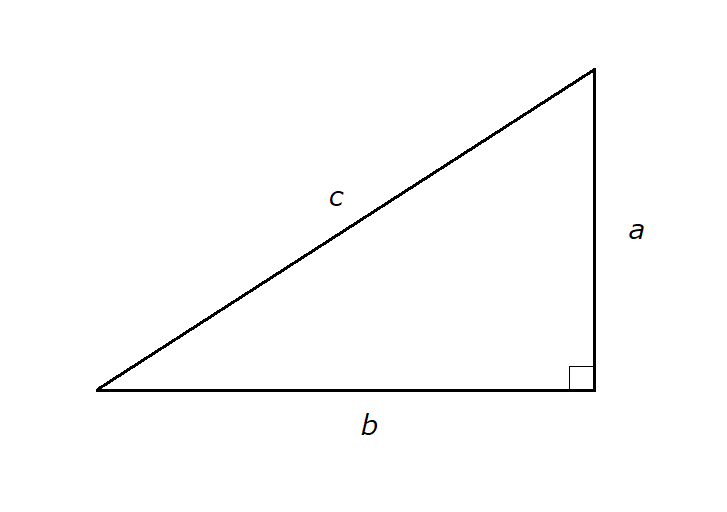
三角形 \( POH \) は直角三角形なので、次のピタゴラスの定理が適用できます。
\[ ピタゴラスの定理（三平方の定理）\]
直角三角形の斜辺の長さを \( c \) 、残りの二辺の長さをそれぞれ \( a \) 、\( b \) とおくと、次式が成り立つ。
\[ c^2 = a^2 + b^2 \]
直角三角形 \( POH \) は斜辺の長さが単位円の半径だから \( 1 \) 、残りの二辺の長さはそれぞれ \( \sin \theta \) 、\( \cos \theta \)
なので、この三角形にピタゴラスの定理を適用すると次の式が導けます。
\[ \sin ^2 \theta + \cos ^2 \theta = 1 \]
※上の式で、
\[ \begin{align}
\sin ^2 \theta &= \left( \sin \theta \right) ^2 \\\\
&= \left( \sin \theta \right) \times \left( \sin \theta \right) \\\\
\cos ^2 \theta &= \left( \cos \theta \right) ^2 \\\\
&= \left( \cos \theta \right) \times \left( \cos \theta \right)
\end{align}\]
という表記法を使っています。
さらに、この式の両辺を \( \cos ^2 \theta \) で割ると、次式も導けます。
さらに、この式の両辺を \( \cos ^2 \theta \) で割ると、次式も導けます。
\[ \tan ^2 \theta + 1 = \frac{1}{\cos ^2 \theta} \]
※ここでも、
\[ \begin{align}
\tan ^2 \theta &= \left( \tan \theta \right) ^2 \\\\
&= \left( \tan \theta \right) \times \left( \tan \theta \right)
\end{align}\]
という表記法を使っています。
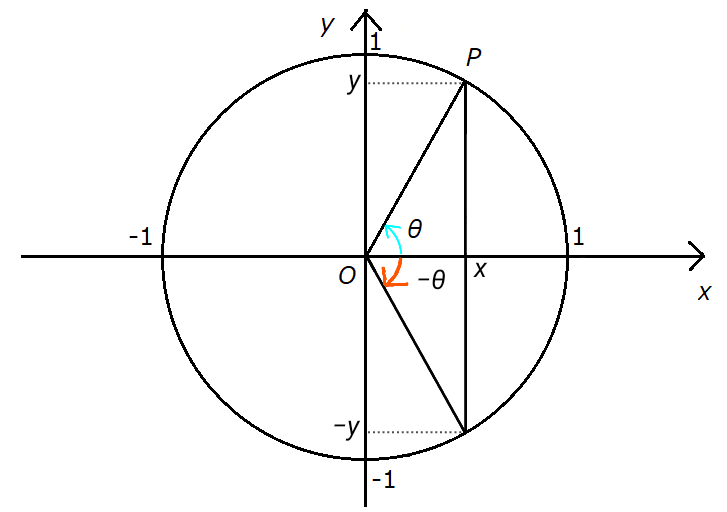
また、一般角 \( - \theta \) は \( \theta \) を \( x \) 軸で折り返したものなので、\( \sin \theta = y \) は符号がプラスからマイナスに反転します。一方、\( \cos \theta = x \) は値が変化しません。図で表すと、下のようになります。
また、一般角 \( - \theta \) は \( \theta \) を \( x \) 軸で折り返したものなので、\( \sin \theta = y \) は符号がプラスからマイナスに反転します。一方、\( \cos \theta = x \) は値が変化しません。図で表すと、下のようになります。
この性質より、次の公式が成り立ちます。
\[ \sin (- \theta ) = - \sin \theta \]
\[ \cos (- \theta ) = \cos \theta \]
\[ \tan (- \theta ) = \frac{\sin (- \theta) }{\cos (- \theta)} = \frac{- \sin \theta }{\cos \theta} = -
\tan \theta \]
ナユミ
三角関数のグラフはどんな感じ？
カヤ
そうだな。まずは、\( \sin \theta \) と \( \cos \theta \) のグラフを見ていこう。
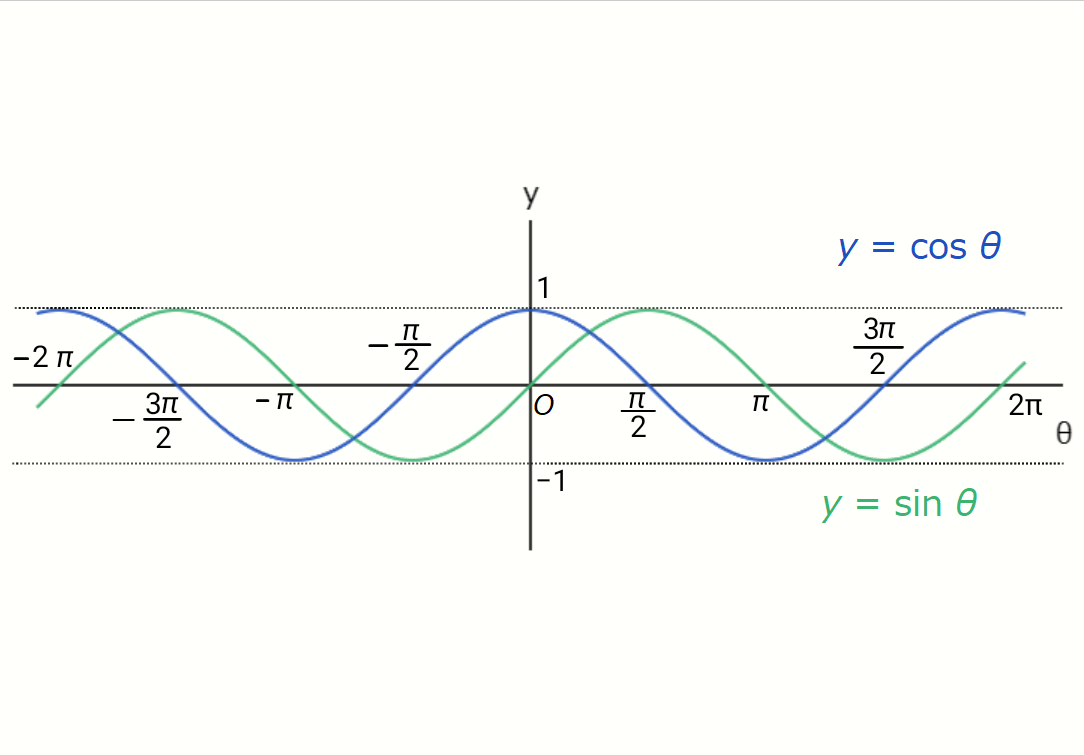
\( y = \sin \theta \) と \( y = \cos \theta \) のグラフはそれぞれ正弦波、余弦波と呼ばれています。
これらの関数はいずれも周期 \( 2 \pi \) の周期関数です。これは、単位円を点 \( P \) が一周して元の場所に戻ると、一般角 \( \theta \) は \( 2 \pi
\) 増えることからわかります。
また、どちらの関数も最大値が \( 1 \) 、最小値が \( -1 \) です。これも、\( \sin \theta \) と \( \cos \theta \) が単位円周上の点 \( P (x,y) \) に対応していたことからわかります。なぜなら、単位円の半径は1だからです。
それから、グラフから読み取れますが、\( y = \sin \theta \) と \( y = \cos \theta \) は、横方向にずらしてあるだけで、形は全く同じのグラフです。この関係を式で書くと、次のようになります。
また、どちらの関数も最大値が \( 1 \) 、最小値が \( -1 \) です。これも、\( \sin \theta \) と \( \cos \theta \) が単位円周上の点 \( P (x,y) \) に対応していたことからわかります。なぜなら、単位円の半径は1だからです。
それから、グラフから読み取れますが、\( y = \sin \theta \) と \( y = \cos \theta \) は、横方向にずらしてあるだけで、形は全く同じのグラフです。この関係を式で書くと、次のようになります。
\[ \sin \theta = \cos \left( \theta - \frac{\pi}{2} \right) \]
\[ \cos \theta = \sin \left( \theta + \frac{\pi}{2} \right) \]
\[ - \sin \theta = \cos \left( \theta + \frac{\pi}{2} \right) \]
\[ - \cos \theta = \sin \left( \theta - \frac{\pi}{2} \right) \]
カヤ
他にもこのグラフから読み取れることはあるが、\( \sin \) と \( \cos \) はこのくらいにして、次は \( \tan \) のグラフに移ろう。
ナユミ
\( \tan \) のグラフはどんなの？
カヤ
これだな。
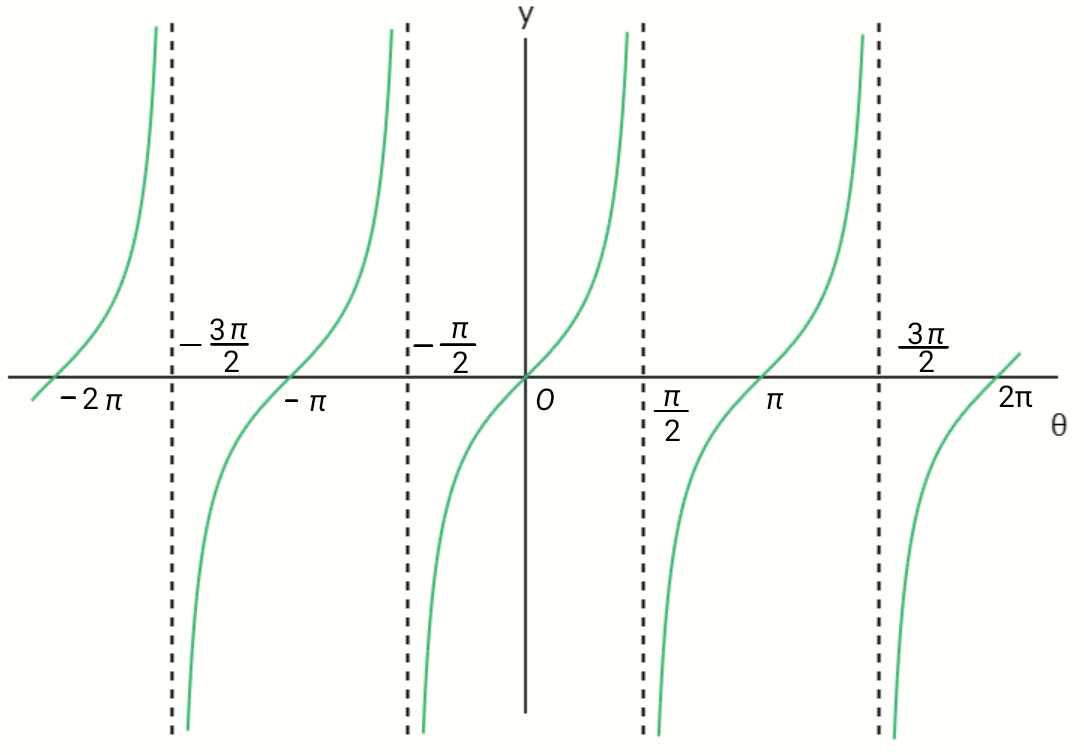
\( y = \tan \theta \) は周期 \( \pi \) の周期関数です。また、\( x = \pm \frac{2n + 1}{2} \pi \ \ (n = 0,1,2, \ldots ) \)
が漸近線になっていて、\( x \) がこれらの値をとるとき、\( \tan \theta \) は定義されません。
ナユミ
なんかコマ送りのフィルムに見えてきたわ。
カヤ
漸近線が縦線だからな。三角関数のグラフはここまでにして、次は加法定理について説明していこう。
加法定理
ナユミ
加法って？
カヤ
加法は足し算のことだ。加法定理は三角関数の変数どうしの足し算についての定理だよ。
\[ 加法定理 \]
\( \alpha \) 、\( \beta \) を一般角として、次が成り立つ。
\[ \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \]
\[ \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \]
\[ \cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \]
\[ \cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \]
\[ \tan ( \alpha + \beta ) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \]
\[ \tan ( \alpha - \beta ) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} \]
ナユミ
がっつり式だらけね。
カヤ
ちょっと証明はややこしいが、いろいろと便利な定理なので、説明しておこう。
まずは、単位円周上に二点 \( P (\cos \beta , \sin \beta) \) 、\( Q (\cos \alpha , \sin \alpha ) \) を取ります。
ここで、\( \angle POA = \beta \) 、\( \angle QOA = \alpha \) とします。
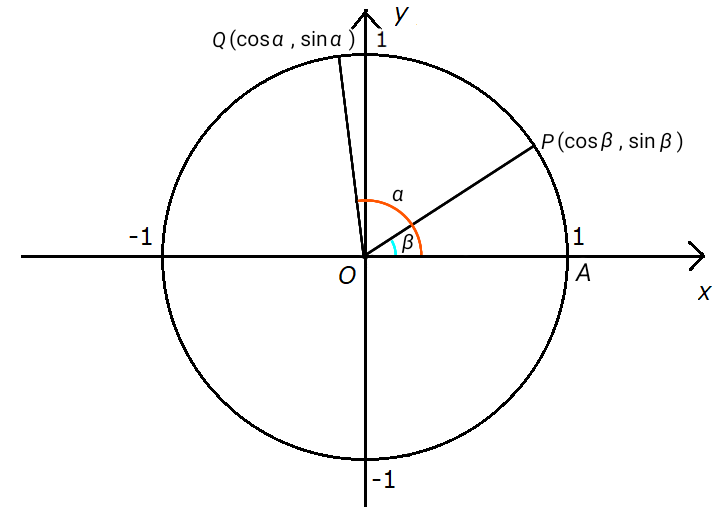
次に三角形 \( OPQ \) を考え、点 \( Q \) から辺 \( OP \) に垂線 \( QH \) を下ろします。
ここで、\[ \angle QOP = \alpha - \beta \]なので、直線 \( OP \) を \( x \) 軸と見立ててみると、\[ QH = \sin ( \alpha - \beta ) \]
\[ OH = \cos ( \alpha - \beta ) \]となることがわかります。
首を左に傾けて、直線 \( OP \) が水平に見えるようにするとわかりやすいと思います。
また、\[ \begin{align}
HP &= OP - OH \\\\
&= 1 - \cos (\alpha - \beta) \end{align} \] が成り立っているので、
三角形 \( QHP \) に三平方の定理を使うと、次の式が求まります。
\[ \begin{align}
PQ^2 &= QH^2 + HP^2 \\\\
&= \sin ^2 (\alpha - \beta ) + (1 - \cos (\alpha - \beta) )^2 \\\\
&= \sin ^2 (\alpha - \beta ) + 1 - 2 \cos (\alpha - \beta) + \cos ^2 (\alpha - \beta) \\\\
&= \left\{ \sin ^2 (\alpha - \beta ) + \cos ^2 (\alpha - \beta) \right\} + 1 - 2 \cos (\alpha - \beta)
\\\\
&= 2 - 2 \cos (\alpha - \beta)
\end{align} \]
\( \sin ^2 (\alpha - \beta ) + \cos ^2 (\alpha - \beta) \) は先ほどピタゴラスの定理より導いた公式
\[ \sin ^2 \theta + \cos ^2 \theta = 1 \]
より1になります。また、\( (1 - \cos (\alpha - \beta) )^2 \) は次の乗法公式によって計算しています。
\[ 乗法公式\]
\[ (a + b)^2 = a^2 + 2ab + b^2 \]
この公式は、次のように分配法則を繰り返し使うと導出できます。
\[ \begin{align}
(a + b)^2 &= (a + b) (a + b) \\\\
&= (a + b) a + (a + b) b \\\\
&= a^2 + ab + ab + b^2 \\\\
&= a^2 + 2ab + b^2
\end{align}\]
ナユミ
なんとか着いていけてるわ。
カヤ
よし。じゃあ続いて、\( PQ^2 \) をもう一つ三角形を作って求めてみよう。
\( x = \cos \beta \) と \( y = \sin \alpha \) との交点を \( R \) とおきます。
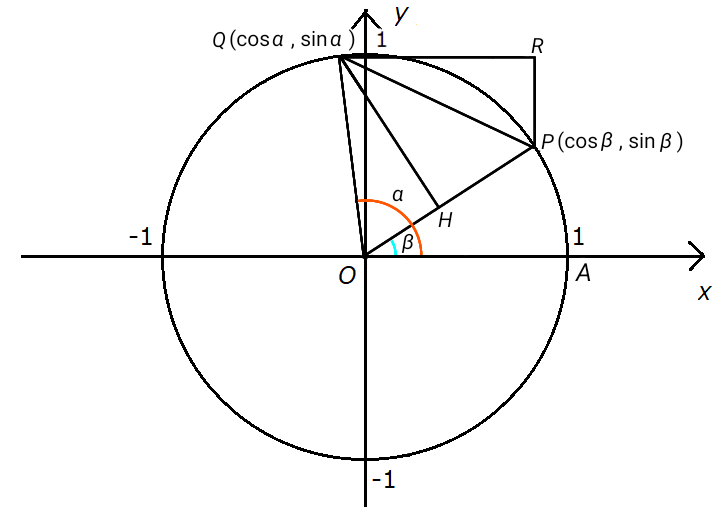
こうしてできる三角形 \( PQR \) に対して三平方の定理を適用すると \( PQ^2 \) を先ほどとは別の形で求められます。
\[ \begin{align}
PQ^2 &= RP^2 + QR^2 \\\\
&= \left( \sin \alpha - \sin \beta \right) ^2 + \left( \cos \alpha - \cos \beta \right) ^2 \\\\
&= \sin ^2 \alpha - 2 \sin \alpha \sin \beta + \sin ^2 \beta + \cos ^2 \alpha - 2 \cos \alpha \cos \beta
+ \cos ^2 \beta \\\\
&= 2 - 2 \left( \sin \alpha \sin \beta + \cos \alpha \cos \beta \right)
\end{align} \]
こうして、\( PQ^2 \) を二通りの方法で求めたわけですが、どちらの方法でも求めた \( PQ^2 \) は同じものなので、これらは等しいはずです。
そこで、次の式が成り立ち、加法定理の公式が一つ求められます。
\[ \begin{align}
2 - 2 \cos (\alpha - \beta) &= 2 - 2 \left( \sin \alpha \sin \beta + \cos \alpha \cos \beta \right) \\\\
\cos (\alpha - \beta) &= \sin \alpha \sin \beta + \cos \alpha \cos \beta
\end{align}\]
ナユミ
達成感あるわ。でも、やっと一つなのね…。
カヤ
ここからは速いから、そんなに心配しなくても大丈夫だぞ。
ナユミ
本当？
カヤ
ああ。まずは、さっき導いた \( \cos (\alpha - \beta) \) の公式に、\( \beta = - \beta \) を代入して式変形してみよう。
\[ \begin{align}
\cos (\alpha - (- \beta ) ) &= \cos \alpha \cos ( - \beta ) + \sin \alpha \sin (- \beta ) \\\\
\cos (\alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta
\end{align} \]
\[ \sin (- \beta ) = - \sin \beta \]
\[ \cos (- \beta ) = \cos \beta \]
を使いました。
ナユミ
これで、\( \cos (\alpha + \beta ) \) の加法定理の公式ができちゃったのね。
カヤ
そうだ。速いだろ。次は、今求めた \( \cos (\alpha + \beta ) \) の公式に、\[ \beta = \beta + \frac{\pi}{2} \]
を代入して式変形してみよう。
\[ \begin{align}
\cos \left( \alpha + \left( \beta + \frac{\pi}{2} \right) \right) &= \cos \alpha \cos \left( \beta +
\frac{\pi}{2} \right) - \sin \alpha \sin \left( \beta + \frac{\pi}{2} \right) \\\\
\cos \left( ( \alpha + \beta ) + \frac{\pi}{2} \right) &= \cos \alpha (- \sin \beta ) - \sin \alpha \cos
\beta \\\\
- \sin ( \alpha + \beta ) &= - \cos \alpha \sin \beta - \sin \alpha \cos \beta \\\\
\sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta
\end{align} \]
\[ \sin \left( \theta + \frac{\pi}{2} \right) = \cos \theta \]
\[ \cos \left( \theta + \frac{\pi}{2} \right) = - \sin \theta \]
を使いました。
カヤ
これで、\( \sin ( \alpha + \beta ) \) の加法定理が求まったな。これに、\( \beta = - \beta \) を代入してみよう。
\[ \begin{align}
\sin (\alpha + (- \beta ) ) &= \sin \alpha \cos ( - \beta ) + \cos \alpha \sin (- \beta ) \\\\
\sin (\alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta
\end{align} \]
ナユミ
\( \sin (\alpha - \beta ) \) の公式が求まったわね。
カヤ
ああ。これで \( \sin \) と \( \cos \) についての加法定理が求まったな。
ナユミ
残りは \( \tan \) ね。
カヤ
\( \tan \) の加法定理は \( \sin \) と \( \cos \) の加法定理から求めることができる。まずは、\( \tan (\alpha + \beta) \) から。
\[ \begin{align}
\tan (\alpha + \beta) &= \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} \\\\
&= \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin
\beta} \\\\
&= \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}
\end{align} \]
2行目から3行目は分母分子を \( \cos \alpha \cos \beta \) で割りました。
ナユミ
ほうほう、うまいこといくものね。
カヤ
そうだな。そして、\( \tan (\alpha - \beta) \) は \( \tan (\alpha + \beta) \) の式に \( \beta = - \beta \) を代入すれば求まる。
\[ \begin{align}
\tan (\alpha + (- \beta)) &= \frac{\tan \alpha + \tan (- \beta)}{1 - \tan \alpha \tan (- \beta) } \\\\
\tan (\alpha - \beta ) &= \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta }
\end{align} \]
\[ \tan ( - \beta ) = - \tan \beta \]
を使いました。
カヤ
これで、\( \sin \) 、\( \cos \) 、\( \tan \) 、すべての加法定理が導出できた。
ナユミ
長かったけど、一個求めたら、後は芋づる式だったわね。
カヤ
そうだろ。じゃあ、次は加法定理から導出できる三角関数の合成公式を紹介しよう。
三角関数の合成
\[ 三角関数の合成 \]
\[ a \sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \sin \left( \theta + \alpha \right) \]
ここで、
\[ \begin{align}
\cos \alpha &= \frac{a}{\sqrt{a^2 + b^2}} \\\\
\sin \alpha &= \frac{b}{\sqrt{a^2 + b^2}}
\end{align}\]
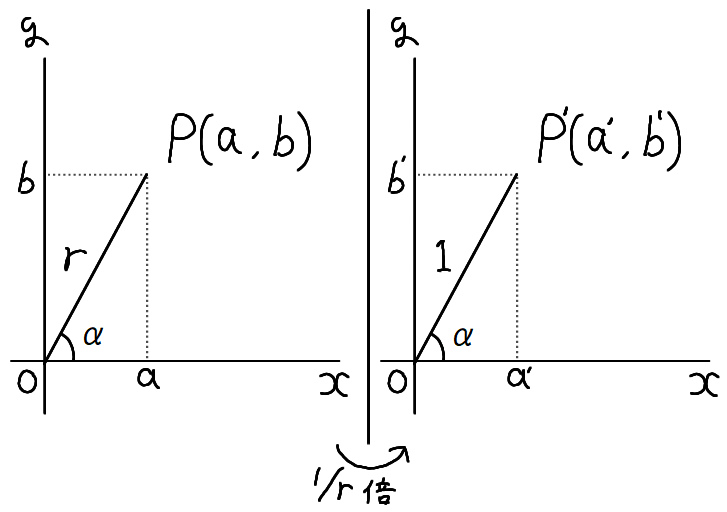
この公式を導くには、まず上図左側のように \( xy \) 座標平面の \( x \) 軸上に点 \( a \) を、\( y \) 軸上に点 \( b \) を取ります。
すると、点 \( P \left( a, b \right) \) について、ピタゴラスの定理より
\[ \begin{align}
OP = r = \sqrt{a^2 + b^2}
\end{align}\]
が成り立ちます。
次に、上図左側の部分を \( x \) 軸方向、\( y \) 軸方向それぞれ \( 1/r \) 倍にします。
これが上図右側の部分で、
\[ \begin{align}
a' &= \frac{a}{r} = \cos \alpha \\\\
b' &= \frac{b}{r} = \sin \alpha
\end{align}\]
が成り立つことがわかります。よって、
\[ \begin{align}
a \sin \theta + b \cos \theta &= r \cos \alpha \sin \theta + r \sin \alpha \cos \theta \\\\
&= r \left( \cos \alpha \sin \theta + \sin \alpha \cos \theta \right) \\\\
&= r \sin \left( \theta + \alpha \right)
\end{align}\]
となり、三角関数の合成公式が成り立つことが証明できました。
ナユミ
同じ角度についてのサインとコサインは、1 個のサインにまとめられるのね。
カヤ
そういうことだな。次は加法定理から導出できる和と積の変換公式を紹介しよう。
和と積の変換公式
ナユミ
加法定理から導出できるんだね。
カヤ
ああ。まずは、積を和に直す公式を紹介しよう。
\[ 積を和に直す公式 \]
\[ \begin{align}
\sin \alpha \cos \beta &= \frac{1}{2} \left\{ \sin (\alpha + \beta) + \sin (\alpha - \beta) \right\}
\\\\
\cos \alpha \sin \beta &= \frac{1}{2} \left\{ \sin (\alpha + \beta) - \sin (\alpha - \beta) \right\}
\\\\
\cos \alpha \cos \beta &= \frac{1}{2} \left\{ \cos (\alpha + \beta) + \cos (\alpha - \beta) \right\}
\\\\
\sin \alpha \sin \beta &= - \frac{1}{2} \left\{ \cos (\alpha + \beta) - \cos (\alpha - \beta) \right\}
\\\\
\end{align}\]
ナユミ
\( \sin \) と \( \cos \) の組み合わせで四種類あるんだね。
カヤ
そうだな。一番上の式から順番に導出していこう。
\[ \begin{align}
\sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\sin (\alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \\
\end{align}\]
の両辺をそれぞれ足し合わせると、
\[ \sin ( \alpha + \beta ) + \sin (\alpha - \beta ) = 2 \sin \alpha \cos \beta \]
両辺を \( 2 \) で割り、右辺と左辺を入れ替えれば、
\[ \sin \alpha \cos \beta = \frac{1}{2} \left\{ \sin (\alpha + \beta) + \sin (\alpha - \beta) \right\}
\]
ナユミ
意外とあっさりね。
カヤ
まあな。上から二番目の式は、次のように両辺をそれぞれ引けばいい。
\[ \begin{align}
\sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\sin (\alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \\
\end{align}\]
の両辺をそれぞれ引くと、
\[ \sin ( \alpha + \beta ) - \sin (\alpha - \beta ) = 2 \cos \alpha \sin \beta \]
両辺を \( 2 \) で割り、右辺と左辺を入れ替えれば、
\[ \cos \alpha \sin \beta = \frac{1}{2} \left\{ \sin (\alpha + \beta) - \sin (\alpha - \beta) \right\}
\]
ナユミ
ほぼいっしょね。
カヤ
三番目の式は、\( \cos \) の加法定理を両辺足し合わせる。
\[ \begin{align}
\cos ( \alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\
\cos (\alpha - \beta ) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{align}\]
の両辺をそれぞれ足し合わせると、
\[ \cos ( \alpha + \beta ) + \cos (\alpha - \beta ) = 2 \cos \alpha \cos \beta \]
両辺を \( 2 \) で割り、右辺と左辺を入れ替えれば、
\[ \cos \alpha \cos \beta = \frac{1}{2} \left\{ \cos (\alpha + \beta) + \cos (\alpha - \beta) \right\}
\]
ナユミ
\( \cos \) 一色ね。
カヤ
そうだな。最後の式は、\( \cos \) の加法定理を両辺引き算だな。
\[ \begin{align}
\cos ( \alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\
\cos (\alpha - \beta ) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{align}\]
の両辺をそれぞれ引くと、
\[ \cos ( \alpha + \beta ) - \cos (\alpha - \beta ) = - 2 \sin \alpha \sin \beta \]
両辺を \( - 2 \) で割り、右辺と左辺を入れ替えれば、
\[ \sin \alpha \sin \beta = - \frac{1}{2} \left\{ \cos (\alpha + \beta) - \cos (\alpha - \beta) \right\}
\]
ナユミ
これだけ \( - \) が出てくるのね。
カヤ
そうだな。これで積を和に直す公式はすべて導出できたので、次は和を積に直す公式に行こう。
\[ 和を積に直す公式 \]
\[ \begin{align}
\sin A + \sin B &= 2 \sin \frac{A+B}{2} \cos \frac{A-B}{2} \\\\
\sin A - \sin B &= 2 \cos \frac{A+B}{2} \sin \frac{A-B}{2} \\\\
\cos A + \cos B &= 2 \cos \frac{A+B}{2} \cos \frac{A-B}{2} \\\\
\cos A - \cos B &= - 2 \sin \frac{A+B}{2} \sin \frac{A-B}{2}
\end{align}\]
ナユミ
これも四種類なのね。
カヤ
和を積に直す公式は、積を和に直す公式を次のように変数変換すればいいだけだ。
積を和に直す公式において、
\[ \alpha + \beta = A \]
\[ \alpha - \beta = B \]
とおく。この二つの式の両辺を足すと、
\[ \alpha = \frac{A+B}{2} \]
が得られ、両辺を引くと、
\[ \beta = \frac{A-B}{2} \]
が得られる。これらを、積を和に直す公式に代入すると、和を積に直す公式が得られる。
ナユミ
ふむふむ。すぐできたわ。
カヤ
見た目はややこしいが、やってみるとそうでもないだろ。
ナユミ
そうね。それにしても、こんな公式いつ使うのかしら？
カヤ
そのうち使うから、心配しなくても大丈夫。
ナユミ
別に心配はしてないわよ。
カヤ
そうかい。それじゃあ、最後にsinc関数についての有名な極限公式を解説して締めくくるとしよう。
sinc関数の極限公式
ナユミ
sinc関数って？
カヤ
sinc関数の定義はこれだな。
\[ {\rm {sinc}} \ x = \frac{\sin x}{x} \]
ナユミ
\( \sin x \) を \( x \) で割ったのね。
カヤ
そうだな。この関数のグラフはこうなる。
ナユミ
お山みたいね。
カヤ
そう見えるな。それで、この関数についての極限公式がこれだ。
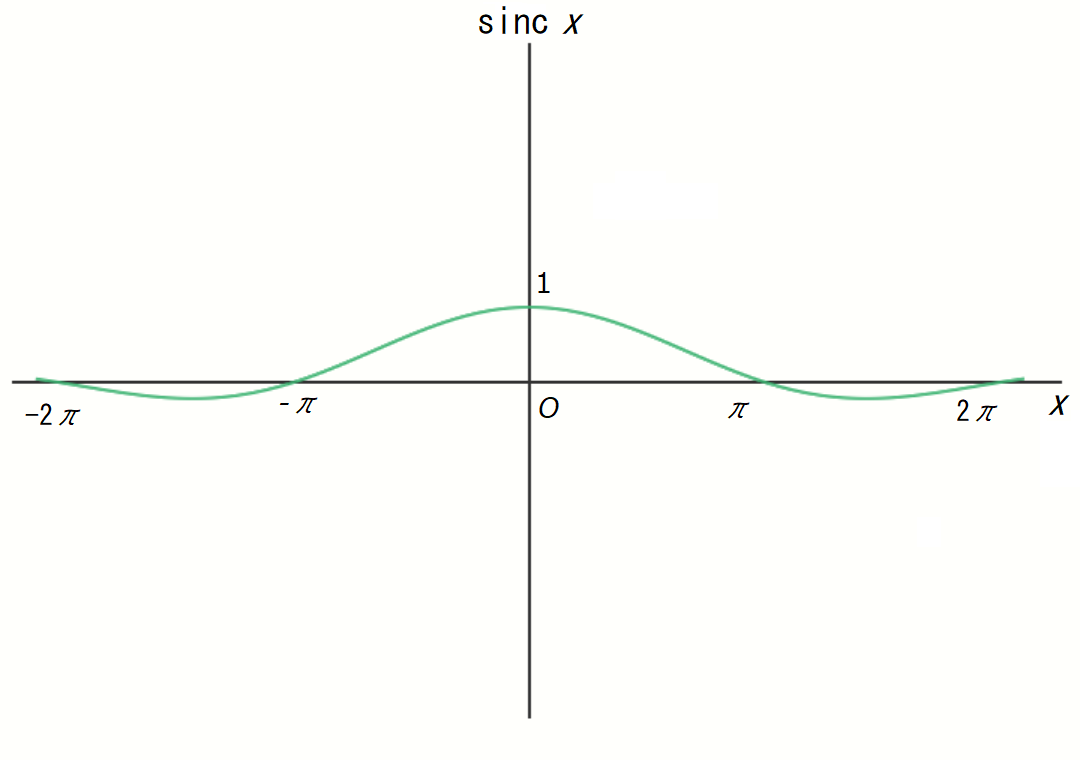
\[ \lim _{x \to 0} \frac{\sin x}{x} = 1 \]
この公式の重要な点は、sinc関数の分母分子ともに、\( x = 0 \) での値が \( 0 \) になりますが、sinc関数にはちゃんと極限値が存在していることです。
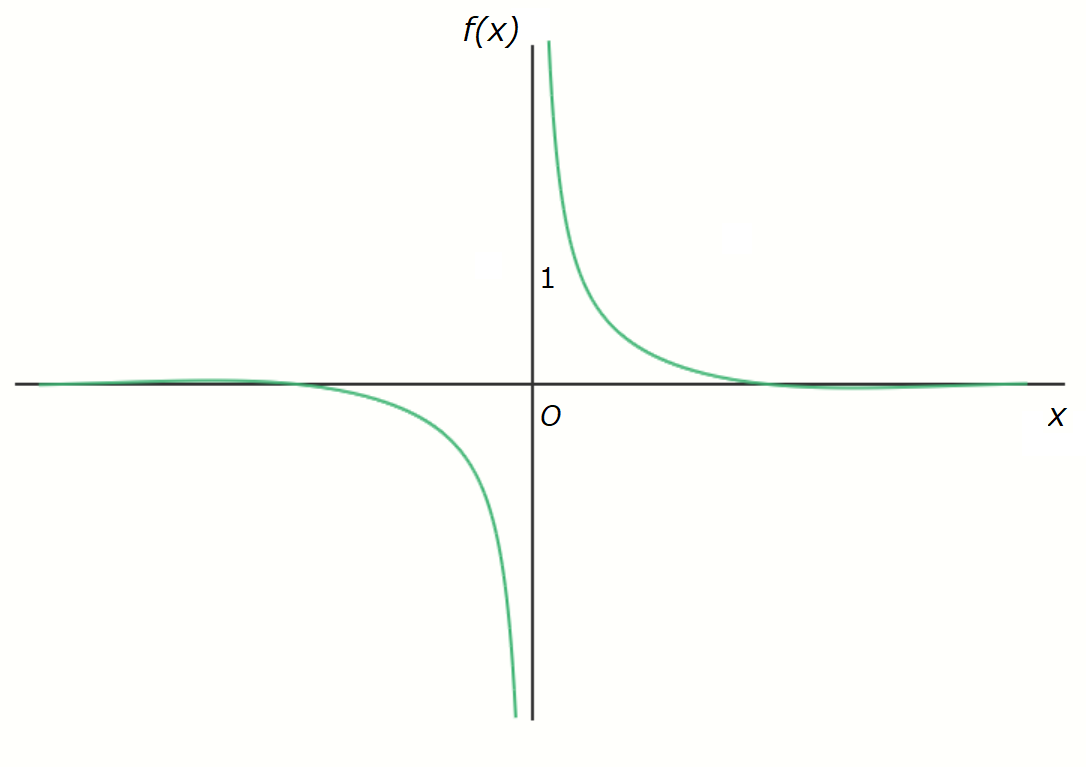
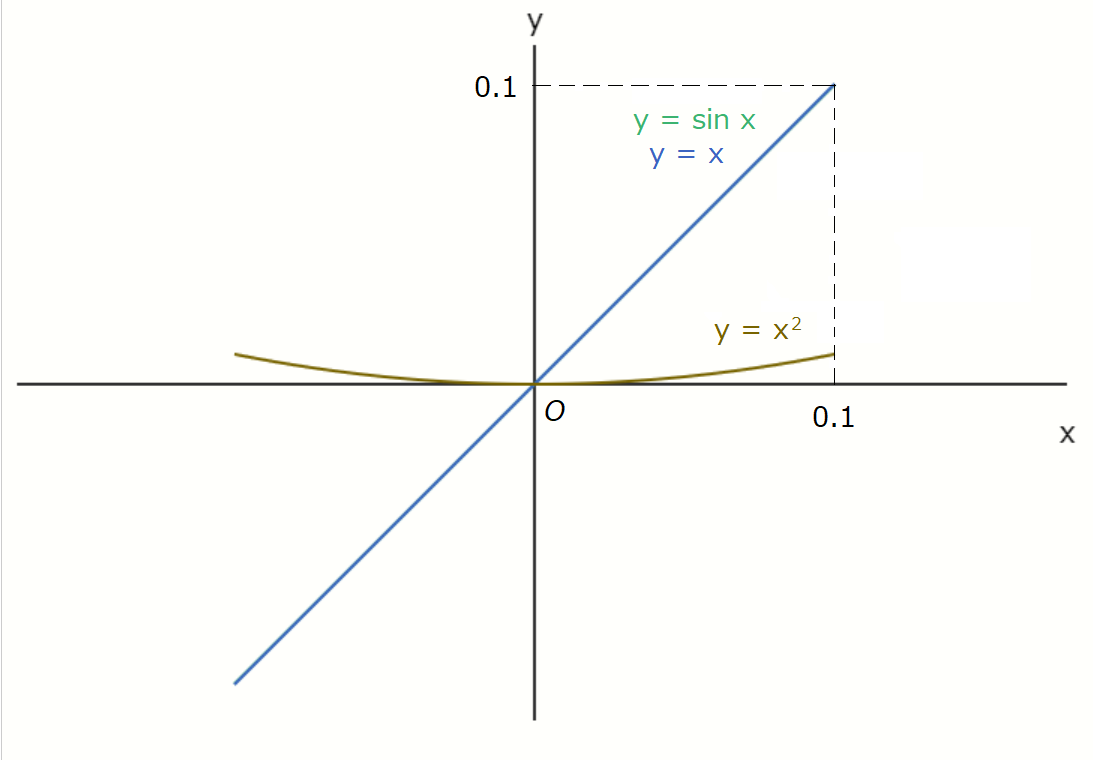
これは、\( 0 \div 0 = 1 \) というような単純な話ではなく、例えば、sinc関数の分母を \( x^2 \) に置き換えた次の関数のグラフを書いてみると、
\( x \to 0 \) で \( 1 \) に収束はしなさそうなことが読み取れます。ですが、この関数も分母分子ともに \( x = 0 \) での値が \( 0 \) になることは確かです。
\[ f(x) = \frac{\sin x}{x^2} \]
この違いは、ざっくりと言うと、\( x = 0 \) の近くでは、\( \sin x \) を \( x \) とみなしても問題ないということです。比較のために、\( \sin x \) 、\( x \) 、\(
x^2 \) のグラフを \( x = 0 \) の近くで書いたグラフを見てみます。
ナユミ
ふうむ、\( x = \frac{1}{2} \) を過ぎたぐらいから、\( \sin x \) と \( x \) は見分けつかなくなってくるわね。でも、\( x = 0 \)
のすっごい近くでは、グラフ三つとも \( y = 0 \) で見分けつかないわよ。
カヤ
そうだな、じゃあこのグラフを \( 10 \) 倍に拡大したものを見てみようか。
ナユミ
\( \sin x \) は \( x \) に重なって見えないわね…。あとは、\( x^2 \) がさっきよりもまっ平に近づいたわ。
カヤ
そう。そして、この拡大を延々と続けていくと、\( \sin x \) と \( x \) はもう区別できないほど重なるのに対して、\( x^2 \)
はまっ平になってしまう。この差が極限値の違いを産んでいるんだ。
ナユミ
\( 0 \) の割り算って難しいのね。
カヤ
そうだな。\( 0 \) の取り扱いは、数学においてはいろいろと難しいことが多い。
ナユミ
まあでもイメージはついたわ。極限公式も済んだし、これで終わりかな？
カヤ
ああ、今回はここまでにしよう。
ナユミ
さんかくさんかく言ってたら、おにぎり食べたくなってきたわ。
カヤ
カヤの分も作っておいてくれ。
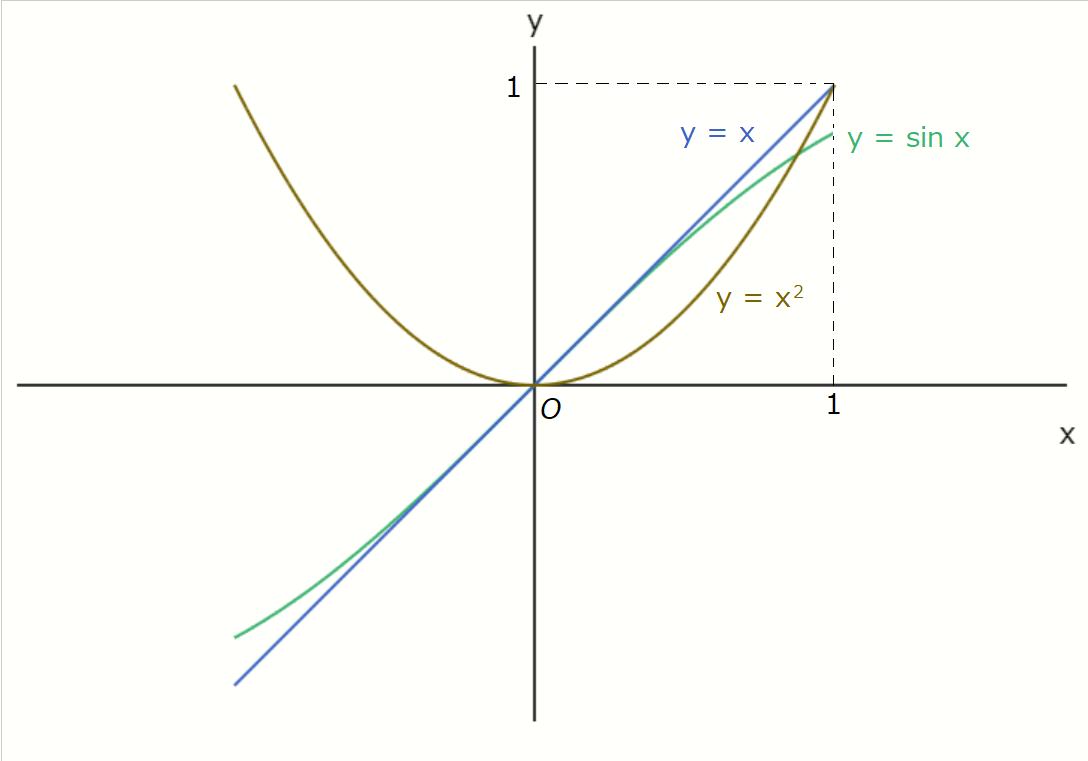
追記：逆三角関数
\[ \begin{align}
逆三角関数
\end{align}\]
関数 \( y= \sin x \) の定義域を \( \left[ - \pi / 2 , \pi / 2 \right] \) に制限したとき、その逆関数を
\[ \begin{align}
y = \sin ^{-1} x \ \ \left( -1 \leq x \leq 1 \right)
\end{align}\]
と書く。同様に、\( y = \cos x \) の定義域を \( \left[ 0 , \pi \right] \) に制限したとき、その逆関数を
\[ \begin{align}
y = \cos ^{-1} x \ \ \left( -1 \leq x \leq 1 \right)
\end{align}\]
と書く。また、\( y = \tan x \) の定義域を \( \left( - \pi / 2 , \pi / 2 \right) \) に制限したとき、その逆関数を
\[ \begin{align}
y = \tan ^{-1} x \ \ \left( - \infty \leq x \leq \infty \right)
\end{align}\]
と書く。\( \sin ^{-1} x \) 、\( \cos ^{-1} x \) 、\( \tan ^{-1} x \) を逆三角関数と呼ぶ。
\( \sin ^{-1} x \) は「アークサイン \( x \) 」または「インバースサイン \( x \) 」と読みます。
\( \cos ^{-1} x \) 、\( \tan ^{-1} x \) も同様の読み方です。
また、逆三角関数を表す別の記号として、
\[ \begin{align}
\arcsin x,\ \arccos x,\ \arctan x
\end{align}\]
も使われます。つまり、
\[ \begin{align}
&\sin ^{-1} x = \arcsin x \\\\
&\cos ^{-1} x = \arccos x \\\\
&\tan ^{-1} x = \arctan x
\end{align}\]
として使われることがあります。
ナユミ
同じ関数でもいろいろな表記が使われるものなのね。
カヤ
数学書を読むときは、記号が意味することが何かをしっかり確認しないと、だな。
参考：
[1] George Allen & Unwin Ltd 著、矢野健太郎 訳補、ブルーバックス 現代数学百科、講談社、1968年11月30日発行
[2] 石村園子、やさしく学べる微分積分、共立出版、1999年12月25日発行
[3] 宮西正宜 他23名、高等学校 数学Ⅱ 改訂版、新興出版社啓林館、2009年12月10日発行
前の記事
第3話
直線・二次曲線
直線・二次曲線
次の記事
第5話
指数・対数関数
指数・対数関数