目次
・数について
カヤ
「数値計算」のコーナーでは、数値実験を理解するために必要な数学の話をしていこうと思う。
ナユミ
数学の話は難しいから、なかなか着いていくのが大変なのだけど。
カヤ
そうだな。数学はさらっとできるようなものではない。でも、一つ一つ順を追って理解していけば、できるようになるものだよ。
ナユミ
うーん、そこまで言うなら頑張るわ。
数について
カヤ
まずは、数について学んでいこう。
日常的に一番馴染み深い数は自然数だと思います。自然数は
\[ 1,2,3 \ldots \]
という数です。普通に物を数えるときに使う数です。自然数に \( 0 \) とマイナス \( (-) \) の符号がついた自然数を加えた数を整数と呼びます。
例えば、\( 3 \) は自然数であり整数でもあります。一方、\( -3 \) は整数ですが、自然数ではありません。
小学校では自然数としての \( 3 \) を引き算するという意味で \( - 3 \) を習ったと思いますが、これをマイナス \( 3 \) という一つの数として捉えることで、例えば \( 2 - 5 \) のような、小さな数から大きな数を引くという計算に対しても解を与えることができるようになります。
ナユミ
自然数と整数と出てきたけど、他の種類の数もまだあるのかしら？
カヤ
日常的に馴染み深い数としては、有理数があるな。
有理数は、有限小数と循環する無限小数からなる数です。有限小数は、いわゆる普通の小数のことで、\( 0.5 \) とか、\( 0.25 \) などを指します。
循環する無限小数は、文字通り数字が循環しながら無限に続く小数のことです。例えば、\( 0.272727 \ldots \) は \( 2 \) と \( 7 \) が無限に繰り替えされています。
繰り返している数字の上に点をつけて、 \( 0.272727 \ldots = 0. \dot{2} \dot{7} \) のように表すこともあります。
任意の有理数は整数同士の比、つまり分母と分子がどちらも整数の分数で表すことができます。 有限小数の場合は、それが整数になるように小数点を右にずらした数を、小数点をずらした回数だけ \( 10 \) で割れば分数で表せます。例えば、 \[ \begin{align} 0.1543 &= \frac{1543}{10 \times 10 \times 10 \times 10} \\\\ &= \frac{1543}{10000} \end{align}\] というようにです。循環する無限小数の場合は少し工夫が必要です。\( 0.123123123 \ldots = 0. \dot{1} 2 \dot{3} \) を具体例にしてやってみます。
任意の有理数は整数同士の比、つまり分母と分子がどちらも整数の分数で表すことができます。 有限小数の場合は、それが整数になるように小数点を右にずらした数を、小数点をずらした回数だけ \( 10 \) で割れば分数で表せます。例えば、 \[ \begin{align} 0.1543 &= \frac{1543}{10 \times 10 \times 10 \times 10} \\\\ &= \frac{1543}{10000} \end{align}\] というようにです。循環する無限小数の場合は少し工夫が必要です。\( 0.123123123 \ldots = 0. \dot{1} 2 \dot{3} \) を具体例にしてやってみます。
\[ \begin{align}
x &= 0.123123123 \ldots \\\\
1000x &= 123.123123 \ldots \\\\
1000x - x &= 123.123123 \ldots - 0.123123123 \ldots \\\\
999x &= 123 \\\\
x &= \frac{123}{999} = 0.123123123 \ldots
\end{align}\]
この方法は上から三行目の計算がポイントで、元の循環する無限小数を \( 1000 \) 倍したものから元の循環する無限小数を引くことで、小数点以下の部分を打ち消しています。
そして、四行目で右辺に残った \( 123 \) と左辺は \( 1000 \) から \( 1 \) 引いて元の無限小数の \( 999 \) 倍なので、\( 123 \div 999 \) で \( x \) 、つまり元の無限小数が得られます。
ナユミ
有理数には色々な表し方があるのね。これで数の種類はすべてかしら？
カヤ
あとは、無理数というものがある。
無理数は循環しない無限小数のことです。有理数と異なり、無理数は整数同士の比で表せません。無理数の身近な例としては、1辺の長さが1の正方形の対角線の長さは \( \sqrt{2} \) という数になり、これは無理数です。\( \sqrt{} \) は根号と呼ばれる記号でルートと読みます。この数は2回かけると2になる数であり、
\[ \sqrt{2} = 1.41421356 \ldots \]
と無限に数が循環せずに続きます。2回かけると2になる数はもう一つあり、それは \( - \sqrt{2} \) です。これは、
\[ \begin{align}
\left( - \sqrt{2} \right) \times \left( - \sqrt{2} \right) &= \left( (-1) \times \sqrt{2} \right) \times \left( (-1) \times \sqrt{2} \right) \\\\
&= (-1) \times (-1) \times \sqrt{2} \times \sqrt{2} \\\\
&= 1 \times 2 \\\\
&= 2
\end{align}\]
というように考えればよいです。かけ算のみからなる式においてかけ算の順序は入れ替えてもよいこと、\( -1 \) をかける操作はプラスマイナスの符号を反転させることに注意してください。
ナユミ
具体的に \( \sqrt{2} \) みたいな無理数を求めるにはどうするの？
カヤ
求め方はいろいろあると思うが、一番原始的な方法はこういうやり方かな。
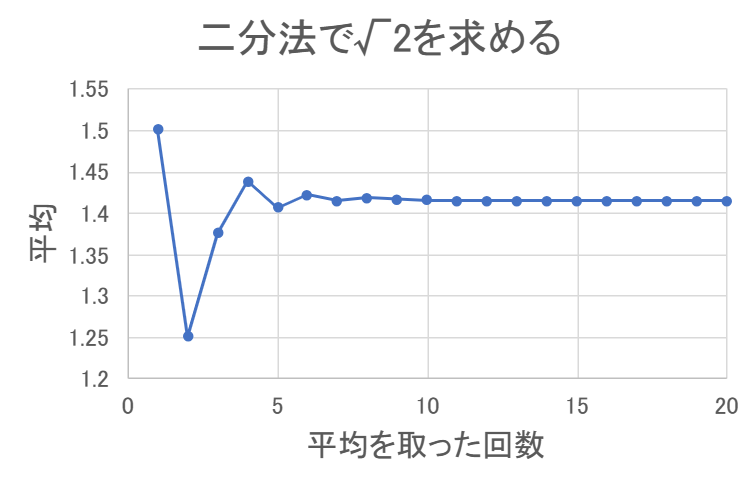
\( (1) \) \( 1 \times 1 = 1 \lt 2 \) 、\( 2 \times 2 = 4 \gt 2 \) より、二回かけると \( 2 \) になる数、つまり \( \sqrt{2} \) は \( 1 \) より大きく \( 2 \) より小さいと考えられる。
\( (2) \) \( 1 \) と \( 2 \) の平均は \( (1 + 2) \div 2 = 1.5 \) 。ここで、\( 1.5 \times 1.5 = 2.25 \gt 2 \) 。よって、 \( \sqrt{2} \) は \( 1 \) より大きく \( 1.5 \) より小さいと考えられる。
\( (3) \) \( 1 \) と \( 1.5 \) の平均は \( (1 + 1.5) \div 2 = 1.25 \) 。ここで、\( 1.25 \times 1.25 = 1.5625 \lt 2 \) 。よって、 \( \sqrt{2} \) は \( 1.25 \) より大きく \( 1.5 \) より小さいと考えられる。
\( (4) \) 以下、同様に二つの数の平均を取り、求めた平均を二回かけたものが \( 2 \) より小さければ一つ前の数のうち小さい方と置き換え、\( 2 \) より大きければ一つ前の数のうち大きい方と置き換え、同じことを繰り返す。
\( (2) \) \( 1 \) と \( 2 \) の平均は \( (1 + 2) \div 2 = 1.5 \) 。ここで、\( 1.5 \times 1.5 = 2.25 \gt 2 \) 。よって、 \( \sqrt{2} \) は \( 1 \) より大きく \( 1.5 \) より小さいと考えられる。
\( (3) \) \( 1 \) と \( 1.5 \) の平均は \( (1 + 1.5) \div 2 = 1.25 \) 。ここで、\( 1.25 \times 1.25 = 1.5625 \lt 2 \) 。よって、 \( \sqrt{2} \) は \( 1.25 \) より大きく \( 1.5 \) より小さいと考えられる。
\( (4) \) 以下、同様に二つの数の平均を取り、求めた平均を二回かけたものが \( 2 \) より小さければ一つ前の数のうち小さい方と置き換え、\( 2 \) より大きければ一つ前の数のうち大きい方と置き換え、同じことを繰り返す。
ナユミ
なるほど…。たしかに、なんというか、いい感じの泥臭さがあるわね。
カヤ
またそのうち解説すると思うが、このやり方は二分法と言われている。実際に平均の計算を \( 20 \) 回目までやってみた結果がこれだ。
ナユミ
本当。ちゃんと1.4くらいのところに落ち着いてるわね。
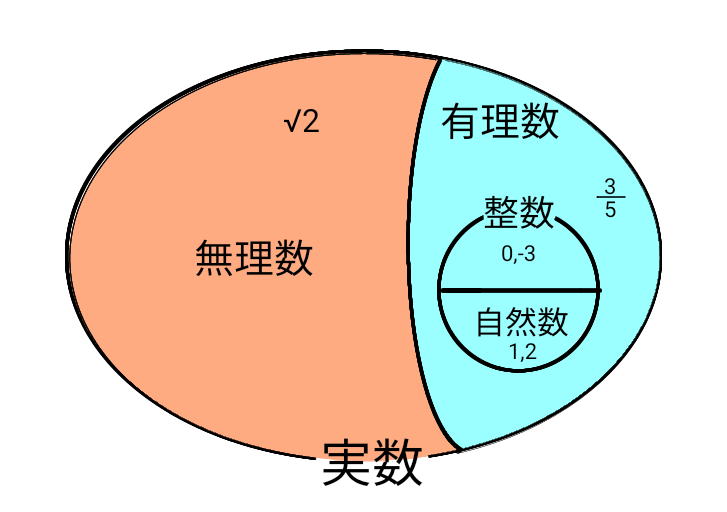
ここまで解説してきた数が、主な数値実験に現れる数になります。自然数、整数、有理数、無理数を一つにまとめて実数と呼んでいます。
参考：
[1] Wikipedia 有理数、https://ja.wikipedia.org/wiki/有理数、2023年7月13日閲覧
[2] George Allen & Unwin Ltd 著、矢野健太郎 訳補、ブルーバックス 現代数学百科、講談社、1968年11月30日発行
次の記事
第2話
一変数関数
一変数関数