目次
・一変数関数
・関数の極限
・関数の連続性
・追記：合成関数・逆関数
カヤ
今回は一変数関数について話していこう。
一変数関数
ナユミ
一変数関数って関数のこと？
カヤ
まあ、普通に関数と言ったら、一変数関数を指すことが多いな。ただ、関数には二つ以上の変数を持つ多変数関数もあるから、ここでは明示的に一変数関数と呼んでいる。
一つの変数 \( x \) の値に応じて、変数 \( y \) の値がただ一つに定まる関係 \( f \) を \( x \) の一変数関数といい、\( y = f(x) \) と表します。
ここで、\( x \) のことを独立変数、\( y \) のことを従属変数と呼びます。
また、\( x \) の値が取り得る範囲のことを定義域、\( y \) の値が取り得る範囲のことを値域と呼びます。特に明記しない限り、定義域は実数全体とすることが多いです。
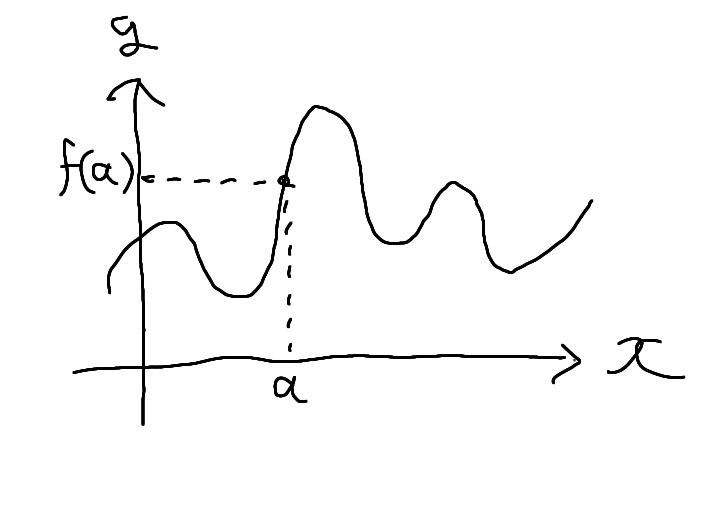
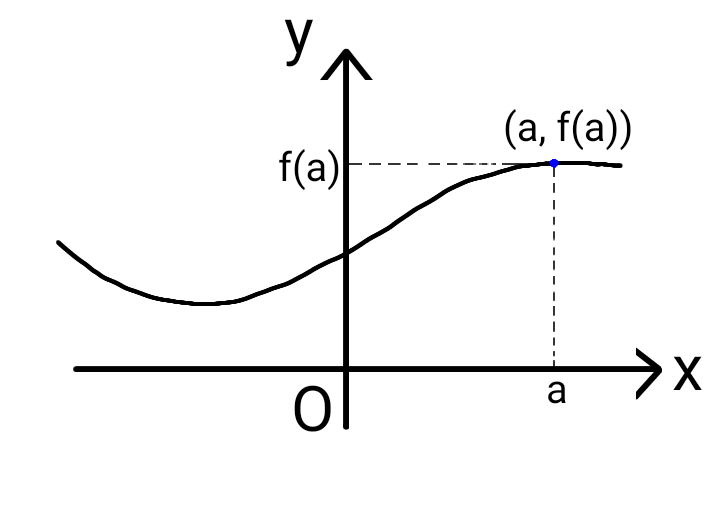
関数 \( y = f(x) \) について、この関係を満たす \( x \) と \( y \) の組からなる点 \( (x,y) \) の全体を関数 \( y = f(x) \) のグラフと呼びます。 グラフを図示すると下のようになり、\( x \) 軸上の値 \( a \) に対応するのが、\( y \) 軸上の値 \( f (a) \) になっています。 \( x \) 軸と \( y \) 軸が交差しているところに書いてある \( O \) は原点を表す記号です。原点は \( (x,y) = (0,0) \) の点に対応しています。
関数 \( y = f(x) \) について、この関係を満たす \( x \) と \( y \) の組からなる点 \( (x,y) \) の全体を関数 \( y = f(x) \) のグラフと呼びます。 グラフを図示すると下のようになり、\( x \) 軸上の値 \( a \) に対応するのが、\( y \) 軸上の値 \( f (a) \) になっています。 \( x \) 軸と \( y \) 軸が交差しているところに書いてある \( O \) は原点を表す記号です。原点は \( (x,y) = (0,0) \) の点に対応しています。
ナユミ
ふむ、一変数関数とそのグラフについてはわかったわ。
カヤ
じゃあ、次は関数の極限について話していこう。
関数の極限
関数 \( y = f(x) \) について、\( x \) が \( x = a \) とならずに限りなく \( a \) に近づくとき、\( y \) の値が限りなく \( b \) に近づくなら、\(
y = f (x) \) は \( x \to a \) のときに \( b \) に収束するという。このとき、\( b \) を極限値と呼び、\[ \lim _{x \to a}
f(x) = b \]と表す。
極限値の定義にある「\( x \) が \( x = a \) とならずに限りなく \( a \) に近づく」という表現は0にまつわるややこしい問題を巧妙に回避するものです。
例えば、瞬間の速さを求める過程を考えてみると、平均の速さにおける時間区間 \( \Delta t \) を限りなく小さくすることで瞬間の速さを求めたわけですが、もしこの時間区間 \( \Delta t \) を \( \Delta t = 0 \) としてしまった場合どうなるでしょう？ 時間区間が \( 0 \) ということは、時間は流れていないので、変化は止まっているはずです。すると、瞬間の速さは \( 0 \) ということになるでしょうか。ですがこの考え方だと、どの瞬間でも時間は流れてないため、瞬間の速さは常に \( 0 \) ということになり変化は起こらなくなってしまいます。
この話は古代ギリシャの哲学者ゼノンが考えたとされる「飛ぶ矢は飛ばない」という話を一般化したものです。 ゼノンは飛んでいる矢のどの瞬間も、その瞬間を切り出せば止まっている矢であることから、飛んでいる矢は常に止まっていると主張しました。 詭弁めいた話ですが、時間区間 \( \Delta t = 0 \) というものを考え始めると、この詭弁のような話に直面してしまうのも事実です。 この問題に直面するのを避けるために、先のような極限値の定義が用いられているのです。
極限値の定義の勘所は、「限りなく \( a \) に近づく」という表現が、ある数にどのくらい近づくかという程度の部分ではなく、ある数にどんどん近づいていくというプロセスに着目した定義であるということです。
例えば、瞬間の速さを求める過程を考えてみると、平均の速さにおける時間区間 \( \Delta t \) を限りなく小さくすることで瞬間の速さを求めたわけですが、もしこの時間区間 \( \Delta t \) を \( \Delta t = 0 \) としてしまった場合どうなるでしょう？ 時間区間が \( 0 \) ということは、時間は流れていないので、変化は止まっているはずです。すると、瞬間の速さは \( 0 \) ということになるでしょうか。ですがこの考え方だと、どの瞬間でも時間は流れてないため、瞬間の速さは常に \( 0 \) ということになり変化は起こらなくなってしまいます。
この話は古代ギリシャの哲学者ゼノンが考えたとされる「飛ぶ矢は飛ばない」という話を一般化したものです。 ゼノンは飛んでいる矢のどの瞬間も、その瞬間を切り出せば止まっている矢であることから、飛んでいる矢は常に止まっていると主張しました。 詭弁めいた話ですが、時間区間 \( \Delta t = 0 \) というものを考え始めると、この詭弁のような話に直面してしまうのも事実です。 この問題に直面するのを避けるために、先のような極限値の定義が用いられているのです。
極限値の定義の勘所は、「限りなく \( a \) に近づく」という表現が、ある数にどのくらい近づくかという程度の部分ではなく、ある数にどんどん近づいていくというプロセスに着目した定義であるということです。
ナユミ
極限って、考え始めると結構面倒な問題なのね…
カヤ
まあな。じゃあ、最後に関数の連続性について話しておこう。
関数の連続性
ナユミ
連続って、何が連続しているの？
カヤ
グラフが連続してるってことさ。
\[ \lim_{x \to a} f(x) = f(a) \]が成り立つとき、関数 \( y = f(x) \) は \( x = a \) で連続であるという。
数値実験で扱う関数は、ほとんどの場合、実数全体で連続であるため、普段は関数の連続性を気にする機会はあまりありません。
ただ、関数の連続性は後に現れる様々な定理の証明の際に重要となる概念のため覚えておくことは重要です。
連続でない関数の例を一応挙げておくと、次の床関数と呼ばれる関数があります。
連続でない関数の例を一応挙げておくと、次の床関数と呼ばれる関数があります。
\[ y = \lfloor x \rfloor \ \ ( \lfloor x \rfloor は \ x \ 以下の最大の整数を表す ) \]
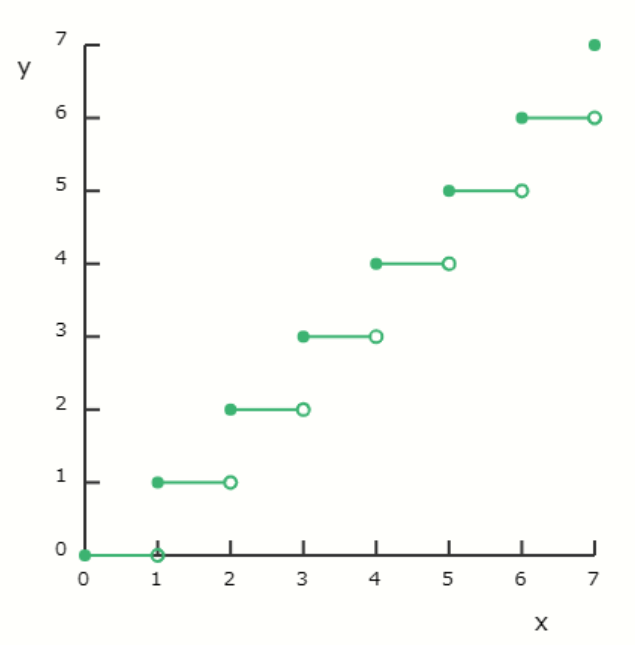
床関数のグラフは \( x = n \ \ (n\ は整数) \) において不連続です。
右側がスカスカなのは、床関数の操作が「小数点以下を切り捨てる」ものだからです。
\( x \) がある整数よりほんのちょっとでも大きかったら、床関数はその整数の値になりますが、\( x \) がある整数よりほんのちょっとでも小さかったら、床関数はその整数より一つ小さい整数になります。
イメージとしては、整数の高さに建物の床があって、その建物の中にある物の真下にある床に応じて物を分類している感じです。
ナユミ
床関数って、時間に厳しい先生みたいね。
カヤ
遅刻厳禁、ってやつだな。
ナユミ
もうちょっとルーズでもいいのに。
追記：合成関数・逆関数
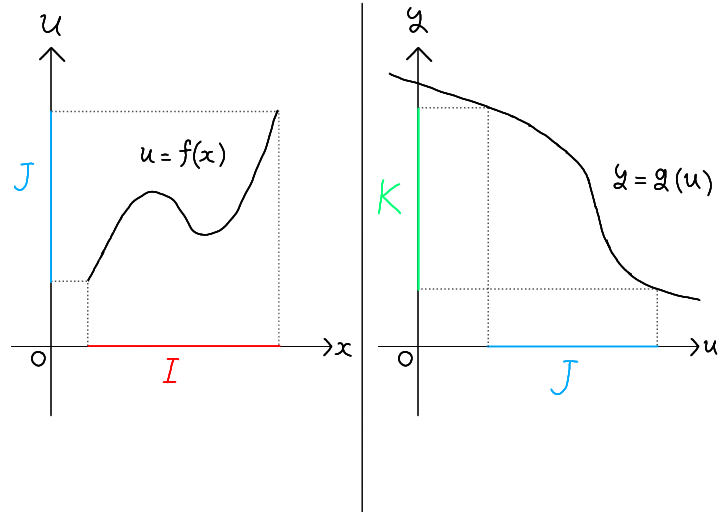
二つの関数 \( u = f(x) \) と \( y = g(u) \) があり、\( u = f(x) \) の値域が \( y = g(u) \) の定義域に含まれるとき、関数 \( y = g(f(x))
\) を定義することができ、これを \( f \) と \( g \) の合成関数と呼びます。
合成関数 \( y = g(f(x)) \) の定義域は \( u = f(x) \) の定義域（下図では \( I \) ）と等しく、値域は \( u = f(x) \) の値域（下図では \( J \) ）を定義域としたときの \( y = g(u) \) の値域（下図では \( K \) ）に等しくなります。
合成関数 \( y = g(f(x)) \) の定義域は \( u = f(x) \) の定義域（下図では \( I \) ）と等しく、値域は \( u = f(x) \) の値域（下図では \( J \) ）を定義域としたときの \( y = g(u) \) の値域（下図では \( K \) ）に等しくなります。
ナユミ
\( I \to J \) 、\( J \to K \) をひとまとめにして、\( I \to K \) にしたってことね。
カヤ
そういうことだな。続いて、逆関数。
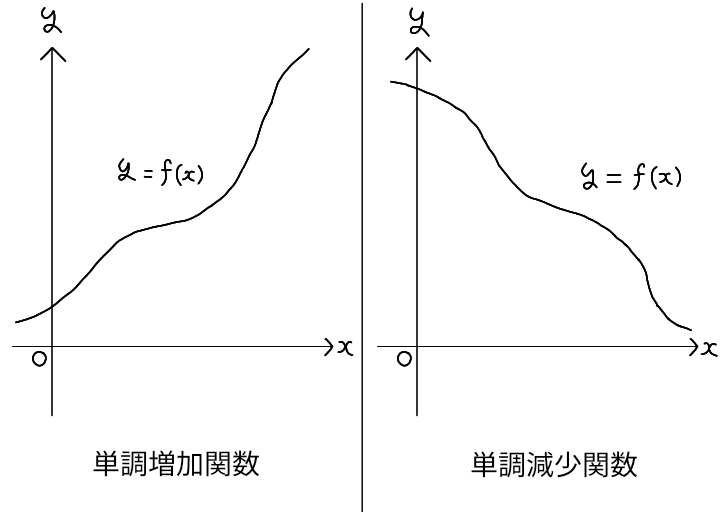
関数 \( y = f(x) \) について、定義域のすべての \( a \leq b \) に対して \( f(a) \leq f(b) \) であるとき、\( f(x) \)
は単調増加関数であると言います。一方、定義域のすべての \( a \leq b \) に対して \( f(a) \geq f(b) \) であるとき、\( f(x) \)
は単調減少関数であると言います。
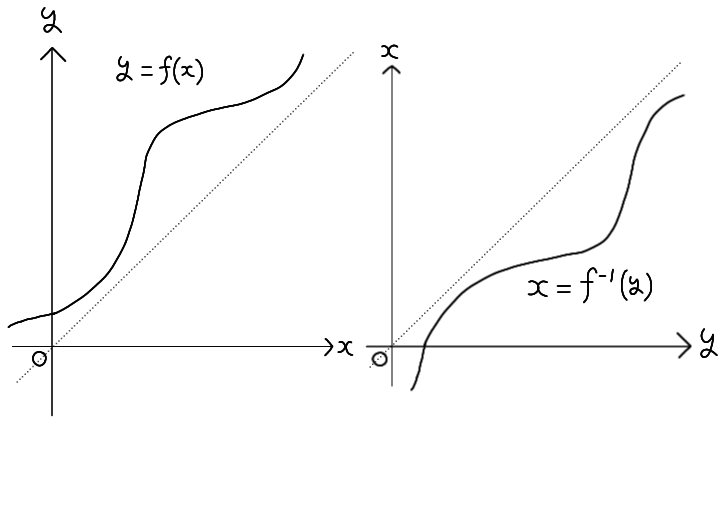
関数 \( y = f(x) \) は定義域上で連続な単調増加（または減少）関数とします。このとき、\( y \) に対し \( x \) を対応させる関数を、関数 \( y = f(x) \)
の逆関数と呼び、\( x = f^{-1} (y) \) と表します。または、\( x \) と \( y \) を入れ替えて、\( y = f^{-1} (x) \) と表します。
\( y = f(x) \) のグラフは \( y=x \) を軸にして折り返すと \( x = f^{-1} (y) \) のグラフになります。
\( y = f(x) \) のグラフは \( y=x \) を軸にして折り返すと \( x = f^{-1} (y) \) のグラフになります。
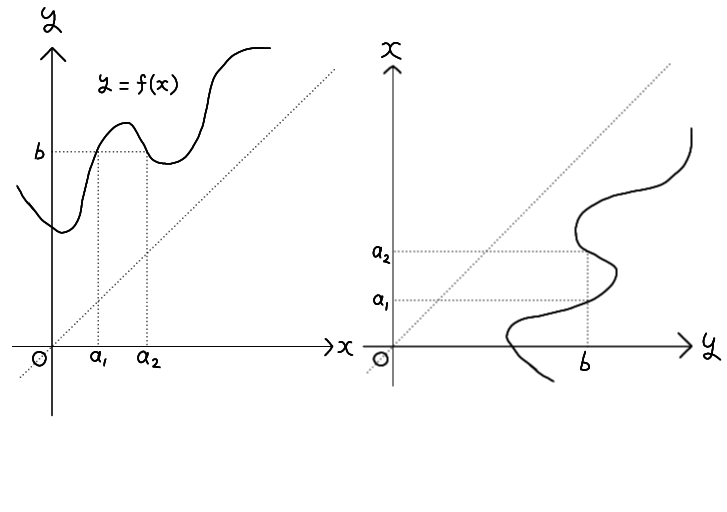
また、\( y=f(x) \) が定義域上で単調増加（または減少）関数でない場合、\( y \) の値に対して \( x \)
の値がただ一つに定まらない箇所が生じるため、逆関数は定義できないことに注意してください。
ナユミ
\( x \) から見ても、\( y \) から見ても、相手が一つのときだけ逆関数が定義できるのね。
カヤ
そういうことだな。
参考：
[1] Wikipedia ゼノンのパラドックス、https://ja.wikipedia.org/wiki/ゼノンのパラドックス、2023年7月15日閲覧
[2] 森毅、位相のこころ、筑摩書房、2006年1月10日発行
[3] 石村園子、やさしく学べる微分積分、共立出版、1999年12月25日発行
[4] 難波 誠、数学シリーズ 微分積分学、裳華房、2009年1月20日発行
前の記事
第1話
数について
数について
次の記事
第3話
直線・二次曲線
直線・二次曲線