目次
・一変数関数の微分
・微分可能性の同値条件
・定数倍と和、差の微分公式
・積と商の微分公式
・合成関数の微分公式
・逆関数の微分公式
カヤ
今回は一変数関数の微分法についての一般論を解説していこう。
一変数関数の微分
\[ 微分係数\]
定義域が \( x = a \) を含む実区間である関数 \( y = f(x) \) について、\[ \lim _{h \to 0} \frac{f(a + h) - f(a)}{h}
\]が存在するならば、\( f(x) \) は \( x = a \) で微分可能であると言い、この極限値を微分係数と呼び \( f ' (a) \) で表す。\( f(x) \)
の \( x = a \) における微分係数は、\( f(x) \) の \( x = a \) における接線の傾きに等しい。
実区間は不等式で表される実数の範囲のことです。
\[ 実区間\]
実数の範囲を表す手法の一つ。変数 \( x \) と定数 \( a \) および \( b \) を含む不等式を用いて、次のように分類される。
\( [a,b] \) ： \( a \leqq x \leqq b \)
\( (a,b] \) ： \( a \lt x \leqq b \)
\( [a,b) \) ： \( a \leqq x \lt b \)
\( (a,b) \) ： \( a \lt x \lt b \)
\( [a,b] \) ： \( a \leqq x \leqq b \)
\( (a,b] \) ： \( a \lt x \leqq b \)
\( [a,b) \) ： \( a \leqq x \lt b \)
\( (a,b) \) ： \( a \lt x \lt b \)
ナユミ
微分係数が接線の傾きというのは？
カヤ
これはグラフを見ながら考えた方がいいだろうな。
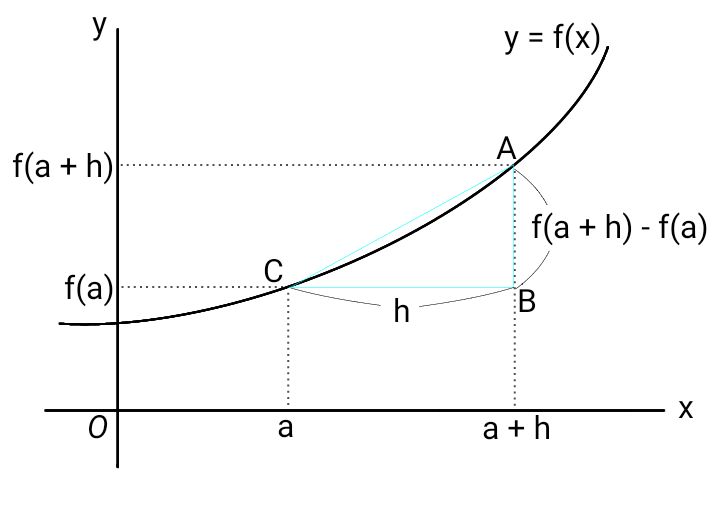
上図を見ると、微分係数の定義に出てくる \[ \frac{f(a + h) - f(a)}{h} \] は \( \rm AC \) の傾きになっています。
\( h \) を \( 0 \) に限りなく近づけたとき、水色の三角形 \( \rm ABC \) は点 \( \rm C \) の位置はそのままに、ものすごく小さくなります。
そのとき、\( \rm AC \) の傾きは \( f(x) \) の \( x = a \) における接線の傾きに等しくなり、この傾きを微分係数と呼びます。
ナユミ
イメージはついたわ。接線の傾きってこうやって求めるのね。
カヤ
接線の傾きを求める方法自体は関数によっては他にもあるが、微分係数は接線の傾きを数式で表現する最も一般的な方法だろうな。
微分係数の定義は \( x \) をある値 \( a \) に近づけた時の極限値なので、\( a \) はその都度定める必要があります。
ですが、これだと一般的な議論がやりにくいので、次のような関数を考えます。
\[ 導関数\]
関数 \( y = f (x) \) がある実区間内のすべての点 \( x \) において微分可能なとき、\( x \) に対してその微分係数 \( f ' (x) \) を対応させる関数を \( y =
f (x) \) の導関数と言い、\( y' \) 、\( f ' (x) \) 、\( \frac{dy}{dx} \) 、\( \frac{df}{dx} \) 、\(
\frac{d}{dx} f (x) \) などと表す。
導関数の表記はいろいろありますが、場合に応じて便利なものを使い分ければよいです。
また、\( y = f(x) \) から、その導関数 \( y = f'(x) \) を求めることを「微分する」と呼びます。
ナユミ
微分するって言ったら、導関数を求めることって思えばいいのね。
カヤ
そうだな。あとは、微分可能という条件について、もう少し考察してみよう。
微分可能性の同値条件
\[ \begin{align}
\text{微分可能性の同値条件}
\end{align}\]
\( y = f(x) \) が \( x=a \) で微分可能なための必要十分条件は、ある \( \delta \gt 0 \) が存在して、
実区間 \( (a - \delta , a + \delta) \) において、\( f(x) \) が次の形に書けることである。
\[ \begin{align}
f(x) = f(a) + (x-a) f'(a) + (x-a) B(x)
\end{align}\]
ここで、\( B(x) \) は \( (a - \delta , a + \delta) \) で定義された関数で、\( x=a \) で連続で、\( B(a) = 0 \) をみたす。
微分可能性の同値条件を証明していきます。
まず、\( f(x) \) が \( x=a \) で微分可能とします。\( B(x) \) を
\[ B(x) =
\begin{cases}
\displaystyle \frac{f(x) - f(a)}{x-a} - f'(a) & (x \neq a) \\[1em]
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 & (x = a)
\end{cases} \]
と定義すると、
\[ \begin{align}
\lim _{x \to a} B(x) &= \lim _{x \to a} \left\{ \frac{f(x) - f(a)}{x-a} - f'(a) \right\} \\\\
&= f'(a) - f'(a) \\\\
&= 0 = B(a)
\end{align}\]
となるため、\( B(x) \) は \( x = a \) で連続であり、実区間 \( (a - \delta , a + \delta) \) において、
\[ \begin{align}
f(x) = f(a) + (x-a) f'(a) + (x-a) B(x)
\end{align}\]
を満たしています。
逆に、\( f(x) \) が実区間 \( (a - \delta , a + \delta) \) において、 \[ \begin{align} f(x) = f(a) + (x-a) A + (x-a) B(x) \end{align}\] の形に書けたとします。ここで、\( A \) は定数とします。 \( x \neq a \) のとき、この式の両辺を \( x - a \) で割ると、 \[ \begin{align} \frac{f(x) - f(a)}{x-a} = A + B(x) \end{align}\] となります。両辺 \( x \to a \) の極限を取ると、\( B(x) \) が \( x = a \) で連続、かつ、\( B(a) = 0 \) を満たすことより、 \[ \begin{align} \lim _{x \to a} \frac{f(x) - f(a)}{x-a} = A = f'(a) \end{align}\] となるため、\( f(x) \) は \( x = a \) で微分可能です。
逆に、\( f(x) \) が実区間 \( (a - \delta , a + \delta) \) において、 \[ \begin{align} f(x) = f(a) + (x-a) A + (x-a) B(x) \end{align}\] の形に書けたとします。ここで、\( A \) は定数とします。 \( x \neq a \) のとき、この式の両辺を \( x - a \) で割ると、 \[ \begin{align} \frac{f(x) - f(a)}{x-a} = A + B(x) \end{align}\] となります。両辺 \( x \to a \) の極限を取ると、\( B(x) \) が \( x = a \) で連続、かつ、\( B(a) = 0 \) を満たすことより、 \[ \begin{align} \lim _{x \to a} \frac{f(x) - f(a)}{x-a} = A = f'(a) \end{align}\] となるため、\( f(x) \) は \( x = a \) で微分可能です。
カヤ
この同値条件は後で使うので、頭の片隅に置いておいてくれ。
ナユミ
ふーん、そうなのね。わかったわ。
カヤ
じゃあ、次は重要な微分公式を紹介していこう。
定数倍と和、差の微分公式
ナユミ
微分公式ってたくさんあるの？
カヤ
いろいろとあるが、ここでは代表的なものに絞って紹介していくことにする。
\[定数倍と和、差の微分公式 \]
関数 \( f(x) \) と \( g(x) \) がある実区間 \( I \) において微分可能なとき、\( c \) を実数定数として、\( cf(x) \) と \( f(x) \pm g(x)
\) も \( I \) で微分可能であり、次式が成り立つ。
\[ \left\{ cf(x) \right\} ' = c f'(x) \]
\[ \left\{ f(x) \pm g(x) \right\} ' = f'(x) \pm g'(x)\]
カヤ
まずは、定数倍の公式の証明。
\[ 定数倍の微分公式の証明\]
\[ \begin{align}
\left\{ cf(x) \right\} ' &= \lim _{h \to 0} \frac{cf(x+h) - cf(x)}{h} \\\\
&= \lim _{h \to 0} \frac{c \left\{ f(x+h) - f(x) \right\} }{h} \\\\
&= c \lim _{h \to 0} \frac{f(x+h) - f(x)}{h} \\\\
&= c f'(x)
\end{align}\]
ナユミ
次は、和と差の公式の証明ね。
\[和と差の微分公式の証明\]
\[ \begin{align}
\left\{ f(x) \pm g(x) \right\} ' &= \lim _{h \to 0} \frac{\left\{ f(x+h) \pm g(x+h) \right\} - \left\{
f(x) \pm g(x) \right\}}{h} \\\\
&= \lim _{h \to 0} \frac{\left\{ f(x+h) - f(x) \right\} \pm \left\{ g(x+h) - g(x) \right\}}{h} \\\\
&= \lim _{h \to 0} \frac{f(x+h) - f(x)}{h} \pm \lim _{h \to 0} \frac{ g(x+h) - g(x)}{h} \\\\
&= f'(x) \pm g'(x)
\end{align}\]
カヤ
引き算するとプラスマイナスが入れ替わることに注意だな。次は積と商の微分公式だ。
積と商の微分公式
\[積と商の微分公式\]
関数 \( f(x) \) と \( g(x) \) がある実区間 \( I \) において微分可能なとき、\( f(x)g(x) \) 、\( \frac{f(x)}{g(x)} \)（ただし、\(
g(x) \neq 0 \) ）も \( I \) で微分可能であり、次式が成り立つ。
\[ \left\{ f(x)g(x) \right\} ' = f'(x)g(x) + f(x)g'(x) \]
\[ \left\{ \frac{f(x)}{g(x)} \right\} ' = \frac{f'(x)g(x) - f(x)g'(x)}{\left\{ g(x) \right\} ^2 } \]
ナユミ
ちょっと、ややこしいわね。
カヤ
さっきよりは少し複雑かな。まずは積の微分から見ていこう。
\[ 積の微分公式の証明\]
\[ \begin{align}
\left\{ f(x)g(x) \right\} ' &= \lim _{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x)}{h} \\\\
&= \lim _{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x+h) + f(x)g(x+h) - f(x)g(x)}{h} \\\\
&= \lim _{h \to 0} \frac{\left\{ f(x+h)- f(x) \right\} g(x+h) + f(x) \left\{ g(x+h) - g(x) \right\}}{h}
\\\\
&= \lim _{h \to 0} \left\{ \frac{f(x+h)- f(x)}{h} g(x+h) + f(x) \frac{ g(x+h) - g(x) }{h} \right\} \\\\
&= f'(x)g(x) + f(x)g'(x)
\end{align}\]
2行目は \[ - f(x)g(x+h) + f(x)g(x+h) \] が分子に追加されていますが、これは同じもののプラスとマイナスだから0なので、勝手に追加しても問題ありません。
これを使って、3行目、4行目で導関数の定義の形が出てくるように式変形しています。
カヤ
次は商の微分を見ていこう。
\[ 商の微分公式の証明\]
\[ \begin{align}
\left\{ \frac{f(x)}{g(x)} \right\} ' &= \lim _{h \to 0} \frac{\frac{f(x+h)}{g(x+h)} -
\frac{f(x)}{g(x)}}{h} \\\\
&= \lim _{h \to 0} \frac{f(x+h)g(x) - f(x)g(x+h)}{hg(x+h)g(x)} \\\\
&= \lim _{h \to 0} \frac{1}{g(x+h)g(x)} \frac{f(x+h)g(x) - f(x)g(x) + f(x)g(x) - f(x)g(x+h)}{h} \\\\
&= \lim _{h \to 0} \frac{1}{g(x+h)g(x)} \frac{\left\{ f(x+h) - f(x) \right\} g(x) - f(x) \left\{ g(x+h)
- g(x) \right\} }{h} \\\\
&= \lim _{h \to 0} \frac{1}{g(x+h)g(x)} \left\{ \frac{f(x+h) - f(x)}{h} g(x) - f(x) \frac{g(x+h) -
g(x)}{h} \right\} \\\\
&= \frac{1}{g(x)g(x)} \left\{ f'(x)g(x) - f(x)g'(x) \right\} \\\\
&= \frac{f'(x)g(x) - f(x)g'(x)}{\left\{ g(x) \right\}^2}
\end{align}\]
3行目では先ほどと同様に分子に\[ - f(x)g(x) + f(x)g(x) \]
という差し引き0の項を加えて、導関数の定義を引き出しています。
カヤ
じゃあ、次は合成関数の微分公式について紹介しよう。
合成関数の微分公式
\[合成関数の微分公式\]
関数 \( u = f(x) \) は実区間 \( I \) において微分可能、関数 \( y = g(u) \) は実区間 \( J \) において微分可能とし、\( u = f(x) \) の値域は
\( J \) に含まれるとする。このとき、合成関数 \( y = g(f(x)) \) は実区間\( I \) において微分可能で、次の式が成り立つ。
\[ y' = g'(u)f'(x) \]
\( y = g(f(x)) \) を合成関数と呼びます。合成関数を定義できるのは、\( f \) の値域が \( g \) の定義域に含まれるときに限られます。
合成関数の微分公式の証明に入る前に、準備として次の定理を証明しておきます。
\( y = f(x) \) が \( x = a \) において微分可能ならば、\( x = a \) において連続である。
ナユミ
連続って久しぶりに聞いたわね。
カヤ
そうだな。証明は次の通りだ。
\( y = f(x) \) が \( x = a \) において連続であることを示すには、
\[ \lim _{x \to a} f(x) = f(a) \]
を示せばよい。そこで、\( x = a + h \) とおくと、\( x \to a \) のとき \( h \to 0 \) なので、
\[ \lim _{h \to 0} f(a+h) = f(a) \]
を示せばよい。仮定より、\( y = f(x) \) は \( x = a \) で微分可能であるから、
\[ \begin{align}
\lim _{h \to 0} \left\{ f(a+h) - f(a) \right\} &= \lim _{h \to 0} \frac{f(a+h) - f(a)}{h} \times h \\\\
&= f'(a) \times 0 = 0
\end{align}\]
よって、
\[ \lim _{h \to 0} f(a+h) = f(a) \]
ナユミ
変数をうまく変換して、微分係数の定義を持ち出しているわね。
カヤ
そういうことだな。それじゃあ、合成関数の微分公式の証明に移ろう。
\[ 合成関数の微分公式の証明\]
仮定より、\( g(u) \) は微分可能なので、
\[ g'(u) = \lim _{k \to 0} \frac{g(u+k) - g(u)}{k} \]
が存在する。ここで、
\[ k = f(x+h) - f(x)\]
とおく。仮定より \( f(x) \) は微分可能であるから、\( f(x) \) は連続である。よって、
\[ \lim _{h \to 0} f(x+h) = f(x) \]
が成り立つから、
\[ \lim _{h \to 0} k = \lim _{h \to 0} \left\{ f(x+h) - f(x) \right\} = 0\]
となる。従って、
\[ \begin{align}
y' &= \lim _{h \to 0} \frac{g(f(x+h))-g(f(x))}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(f(x)+k)-g(f(x))}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(u+k)-g(u)}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(u+k)-g(u)}{k} \times \frac{k}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(u+k)-g(u)}{k} \times \frac{f(x+h) - f(x)}{h} \\\\
&= g'(u)f'(x)
\end{align}\]
カヤ
それじゃあ、最後に逆関数の微分公式に取り組んでおこう。
逆関数の微分公式
\[逆関数の微分公式\]
関数 \( y = f(x) \) は実区間 \( I \) において単調増加（または減少）関数であり、\( I \) において微分可能とする。
このとき、逆関数 \( x = f^{-1} (y) \) は \( f'(x) \neq 0 \) となる \( x \) に対応する \( y \) で微分可能であり、次の式が成り立つ。
\[ x' = \frac{1}{y'} \]
ナユミ
逆関数の微分は元の関数の微分の逆数になっているのね。
カヤ
そういうことだな。証明は次の通りだ。
\[逆関数の微分公式の証明\]
実区間 \( I \) に含まれ、\( f'(a) \neq 0 \) を満たす \( a \) について考える。
\( b=f(a) \) とおく。\( y=f(x) \) は \( x=a \) で微分可能であるから、
ある \( \delta \gt 0 \) が存在して、
実区間 \( (a - \delta , a + \delta) \) において、次の形に書ける。
\[ \begin{align}
y - b = (x-a) f'(a) + (x-a) B(x)
\end{align}\]
ここで、\( B(x) \) は \( (a - \delta , a + \delta) \) で定義された関数で、\( x=a \) で連続で、\( B(a) = 0 \) をみたす。
\( f'(a) \neq 0 \) 、\( x = f^{-1} (y) \) に注意すると、
\[ \begin{align}
y - b &= \left( f^{-1} (y) - a \right) f'(a) + \left( f^{-1} (y) -a \right) B\left( f^{-1} (y)
\right) \\\\
f^{-1} (y) - a &= \frac{1}{f'(a)} \left( y-b \right) - \frac{1}{f'(a)} \cdot \left( f^{-1} (y) -a
\right) B\left( f^{-1} (y) \right) \\\\
&= \left( y-b \right) \cdot \frac{1}{f'(a)} + \left( y-b \right) \cdot \frac{\left( f^{-1} (y) -a
\right) B\left( f^{-1} (y) \right)}{f'(a)\left( b-y \right)} \\\\
&= \left( y-b \right) \cdot \frac{1}{f'(a)} + \left( y-b \right) \cdot \frac{-B\left( f^{-1} (y)
\right)}{f'(a) \left\{ f'(a) + B\left( f^{-1} (y) \right) \right\}}
\end{align}\]
ここで、
\[ \begin{align}
C(y) = \frac{-B\left( f^{-1} (y) \right)}{f'(a) \left\{ f'(a) + B\left( f^{-1} (y) \right) \right\}}
\end{align}\]
と置くと、この関数は \( C(b) = 0 \) を満たし、\( y=b \) で連続である。
ゆえに、逆関数 \( x= f^{-1} (y) \) は \( y=b \) で微分可能で、
\[ x' = \frac{1}{y'} \]
が成り立つ。
また、逆関数の微分公式を次のように「説明」することもできます。
\[逆関数の微分公式の説明\]
実区間 \( I \) において、関数 \( x = f^{-1} (y) \) の両辺を \( x \) で微分すると、
\[ \begin{align}
\frac{d}{dx} (x) &= \frac{d}{dx} f^{-1} (y)
\end{align}\]
合成関数の微分公式より、
\[ \begin{align}
1 &= \frac{df^{-1} (y)}{dy} \cdot \frac{dy}{dx}
\end{align}\]
よって、\( dy/dx \neq 0 \) であるなら、
\[ \begin{align}
\frac{df^{-1} (y)}{dy} &= \cfrac{1}{\cfrac{dy}{dx}} \\\\
\frac{dx}{dy} &= \cfrac{1}{\cfrac{dy}{dx}} \\\\
x' &= \frac{1}{y'}
\end{align}\]
が成り立つ。
上の説明の中で、\( x = f^{-1} (y) \) が微分可能であることが不明なまま合成関数の微分公式を使っているため、これは証明とは言えませんが、逆関数の微分公式を思い起こすには便利な説明です。
ナユミ
これで微分公式はおわり？
カヤ
ああ。次回は三角関数などの具体的な関数の微分についてやっていこう。
参考：
[1] George Allen & Unwin Ltd 著、矢野健太郎 訳補、ブルーバックス 現代数学百科、講談社、1968年11月30日発行
[2] 石村園子、やさしく学べる微分積分、共立出版、1999年12月25日発行
[3] 難波 誠、数学シリーズ 微分積分学、裳華房、2009年1月20日発行
前の記事
第5話
指数・対数関数
指数・対数関数
次の記事
第7話
様々な関数の微分
様々な関数の微分