目次
・2次元消散型波動方程式
・方程式の離散化
・境界条件
・振動の分布関数
・計算例
ナユミ
あら、かわいいアヒルちゃんね。
カヤ
そうだろう。2次元消散型波動方程式のシミュレーションをしているんだ。
―説明書―
2次元消散型波動方程式のシミュレータです。
[1] 表示画面下の設定項目について
\( c_1 \) ：第1相の位相速度
\( c_2 \) ：第2相の位相速度
\( p \) ：減衰係数
\( \alpha \) ：振動子の分布関数の裾野の広がり
\( A_1 \) ：振動子1の分布関数の最大値
\( A_2 \) ：振動子2の分布関数の最大値
\( \tau _1 \) ：振動子1の振動周期
\( \tau _2 \) ：振動子2の振動周期
スリット ：中央のスリット幅
境界 ：境界条件。なお、無反射の場合スリット周りについては自由端扱いです。
モード ：媒質を1相および2相から選べます。アヒルモードはアヒルが泳ぎます。
色相：媒質の色相
明暗比 ：波のコントラスト。波が高いほど明るく、低いほど暗く表示されます。
視点 ：真上、斜め、斜め(ワイヤー)。なお、アヒルの観察は真上からのみです。
セット ：パラメータをプリセットに設定します。
[2] 表示画面について
表示画面上の●は振動子です。青色が振動子1、朱色が振動子2です。マウスでドラッグすると動かせます。 「開始/停止」ボタンを押す前は視点は真上で固定されています。ボタンを押すとシミュレーションが始まり、選択した視点で結果が表示されます。 また、視点が真上のときに表示画面の媒質部分をクリックすると波に振動を与えることができます。
2次元消散型波動方程式のシミュレータです。
[1] 表示画面下の設定項目について
\( c_1 \) ：第1相の位相速度
\( c_2 \) ：第2相の位相速度
\( p \) ：減衰係数
\( \alpha \) ：振動子の分布関数の裾野の広がり
\( A_1 \) ：振動子1の分布関数の最大値
\( A_2 \) ：振動子2の分布関数の最大値
\( \tau _1 \) ：振動子1の振動周期
\( \tau _2 \) ：振動子2の振動周期
スリット ：中央のスリット幅
境界 ：境界条件。なお、無反射の場合スリット周りについては自由端扱いです。
モード ：媒質を1相および2相から選べます。アヒルモードはアヒルが泳ぎます。
色相：媒質の色相
明暗比 ：波のコントラスト。波が高いほど明るく、低いほど暗く表示されます。
視点 ：真上、斜め、斜め(ワイヤー)。なお、アヒルの観察は真上からのみです。
セット ：パラメータをプリセットに設定します。
[2] 表示画面について
表示画面上の●は振動子です。青色が振動子1、朱色が振動子2です。マウスでドラッグすると動かせます。 「開始/停止」ボタンを押す前は視点は真上で固定されています。ボタンを押すとシミュレーションが始まり、選択した視点で結果が表示されます。 また、視点が真上のときに表示画面の媒質部分をクリックすると波に振動を与えることができます。
ナユミ
ふーむ、アヒルちゃんはともかくとして、水面の波は波動方程式っていうので描いてるのかな？
カヤ
そういうことだな。以下ではこの方程式について解説していこう。
2次元消散型波動方程式
波動方程式は音波、水面波、電磁波などの波動と呼ばれる現象を表す基本的な偏微分方程式です。
2次元の波動方程式は、
\[ \frac{\partial ^2 u}{\partial t^2} = c^2 \left( \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2
u}{\partial y^2} \right)\]
という形で表されます。ここで、\( u \) は波の高さ、\( c \) は位相速度と呼ばれる非負の実数定数です。
波動方程式に消散（摩擦）の効果を加えたものを消散型波動方程式と呼びます。 消散型波動方程式にはいくつかの種類がありますが、ここでは次式を用いています。 \[ \frac{\partial ^2 u}{\partial t^2} = c^2 \left( \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} \right) - p \frac{\partial u}{\partial t} \] ここで、\( p \) は正の実数定数で減衰係数と呼ぶことにします。
波動方程式に消散（摩擦）の効果を加えたものを消散型波動方程式と呼びます。 消散型波動方程式にはいくつかの種類がありますが、ここでは次式を用いています。 \[ \frac{\partial ^2 u}{\partial t^2} = c^2 \left( \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} \right) - p \frac{\partial u}{\partial t} \] ここで、\( p \) は正の実数定数で減衰係数と呼ぶことにします。
ナユミ
いろいろな現象が波動方程式で表せるのね。
カヤ
そうだな。続いて、波動方程式を陽的差分法で解く準備をしていこう。まずは方程式の離散化から。
方程式の離散化
ここでは、消散型波動方程式を差分近似を用いて離散化します。まずは、方程式に現れる各偏導関数をそれぞれ差分近似で表してみます。
\[ \begin{align}
\frac{\partial u}{\partial t} & \cong \frac{u \left( x , y , t \right) - u \left( x , y , t - \Delta t
\right)}{\Delta t} \\\\
\frac{\partial ^2 u}{\partial t^2} & \cong \frac{u \left( x , y , t + \Delta t \right) - 2 u \left( x, y
, t \right) + u \left( x , y , t - \Delta t \right)}{\left( \Delta t \right) ^2} \\\\
\frac{\partial ^2 u}{\partial x^2} & \cong \frac{u \left( x + h , y , t \right) - 2 u \left( x , y , t
\right) + u \left( x - h , y , t \right)}{h ^2} \\\\
\frac{\partial ^2 u}{\partial y^2} & \cong \frac{u \left( x , y + h, t \right) - 2 u \left( x , y , t
\right) + u \left( x , y - h, t \right)}{h ^2}
\end{align}\]
ここで、\( \partial u / \partial t \) は後退差分近似、それ以外は中心差分近似により与えています。
また、時間の離散化幅は \( \Delta t \) で、空間の離散化幅は \( h \) でそれぞれ表しています。
これらの近似式を用いて消散型波動方程式を離散化したものが次式です。
\[ \begin{align}
u \left( x , y , t + \Delta t \right) = \ & 2 u \left( x , y , t \right) - u \left( x , y , t - \Delta t
\right) \\\\
& + \frac{c^2 \left( \Delta t \right) ^2 }{h^2} \cdot \left\{ u \left( x + h, y , t \right) + u \left( x
- h, y , t \right) + u \left( x , y + h, t \right) + u \left( x , y - h, t \right) - 4 u \left( x , y ,
t \right) \right\} \\\\
& -p \Delta t \left\{ u \left( x , y , t \right) - u \left( x , y , t - \Delta t \right) \right\}
\end{align}\]
続いて、計算領域を設定します。ここでは、一辺の長さが \( L \) の正方形領域を対象として離散化を行います。
時刻については、
\[ t_n = n \Delta t \ \ \left( n = 0, 1, \ldots \right)\]
位置については、
\[ \begin{align}
x_i = i h \ \ \left( i = 0, 1, \ldots , m \right) \\\\
y_j = j h \ \ \left( j = 0, 1, \ldots , m \right)
\end{align}\]
ただし、\( mh = L \) とします。これらの式を先ほどの離散化した式に代入して、消散型波動方程式の陽的公式を得ます。
\[ 消散型波動方程式の陽的公式\]
\[ \begin{align}
u \left( x_i , y_j , t_{n+1} \right) = \ & 2 u \left( x_i , y_j , t_n \right) - u \left( x_i , y_j ,
t_{n-1}
\right) \\\\
& + \frac{c^2 \left( \Delta t \right) ^2 }{h^2} \cdot \left\{ u \left( x_{i+1}, y_j , t_n \right) + u
\left( x
_{i-1}, y_j , t_n \right) + u \left( x_i , y_{j+1}, t_n \right) + u \left( x_i , y_{j-1}, t_n \right) -
4 u \left( x_i , y_j ,
t_n \right) \right\} \\\\
& -p \Delta t \left\{ u \left( x_i , y_j , t_n \right) - u \left( x_i , y_j , t_{n-1} \right) \right\}
\end{align}\]
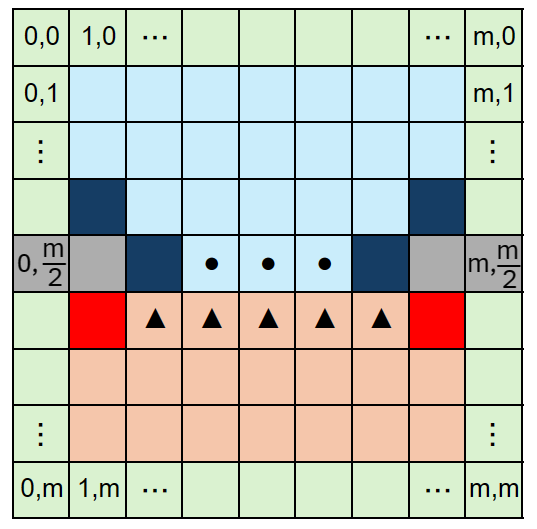
ここで一つ補足があります。冒頭のシミュレータは空間を上図のように離散化しています。
ここで、\( m \) は便宜上偶数とします。\( j = \frac{m}{2} \) の位置にはスリットがあり、これより上側が第1相、下側が第2相としています。
陽的公式を適用するのは水色で塗られたマスと、オレンジ色で塗られたマスです。それ以外のマスは後で説明する境界条件の式により時間発展を計算します。 注意してほしいのは●と▲が描かれたマスの計算です。このマスは隣接する4マスに第1相と第2相が混在しているため、陽的公式に現れる位相速度 \( c \) を第1相と第2相で分けて考えます。 第1相の位相速度を \( c_1 \) 、第2相の位相速度を \( c_2 \) とすれば、●と▲が描かれたマスの陽的公式は以下のようになります。
陽的公式を適用するのは水色で塗られたマスと、オレンジ色で塗られたマスです。それ以外のマスは後で説明する境界条件の式により時間発展を計算します。 注意してほしいのは●と▲が描かれたマスの計算です。このマスは隣接する4マスに第1相と第2相が混在しているため、陽的公式に現れる位相速度 \( c \) を第1相と第2相で分けて考えます。 第1相の位相速度を \( c_1 \) 、第2相の位相速度を \( c_2 \) とすれば、●と▲が描かれたマスの陽的公式は以下のようになります。
●が描かれたマス
\[ \begin{align}
u \left( x_i , y_j , t_{n+1} \right) = \ & 2 u \left( x_i , y_j , t_n \right) - u \left( x_i , y_j ,
t_{n-1}
\right) \\\\
& + \frac{c_1 ^2 \left( \Delta t \right) ^2 }{h^2} \cdot \left\{ u \left( x_{i+1}, y_j , t_n \right) + u
\left( x
_{i-1}, y_j , t_n \right) + u \left( x_i , y_{j-1}, t_n \right) -
3 u \left( x_i , y_j ,
t_n \right) \right\} \\\\
& + \frac{c_2 ^2 \left( \Delta t \right) ^2 }{h^2} \cdot \left\{ u \left( x_i , y_{j+1}, t_n \right) -
u \left( x_i , y_j ,
t_n \right) \right\} \\\\
& -p \Delta t \left\{ u \left( x_i , y_j , t_n \right) - u \left( x_i , y_j , t_{n-1} \right) \right\}
\end{align}\]
▲が描かれたマス
\[ \begin{align}
u \left( x_i , y_j , t_{n+1} \right) = \ & 2 u \left( x_i , y_j , t_n \right) - u \left( x_i , y_j ,
t_{n-1}
\right) \\\\
& + \frac{c_1 ^2 \left( \Delta t \right) ^2 }{h^2} \cdot \left\{ u \left( x_i , y_{j-1}, t_n \right) -
u \left( x_i , y_j ,
t_n \right) \right\} \\\\
& + \frac{c_2 ^2 \left( \Delta t \right) ^2 }{h^2} \cdot \left\{ u \left( x_{i+1} , y_j, t_n \right) + u
\left( x_{i-1} , y_j, t_n \right) + u \left( x_i , y_{j+1}, t_n \right) -3
u \left( x_i , y_j ,
t_n \right) \right\} \\\\
& -p \Delta t \left\{ u \left( x_i , y_j , t_n \right) - u \left( x_i , y_j , t_{n-1} \right) \right\}
\end{align}\]
ナユミ
結構長めの式になったわね。
カヤ
時間も空間も2次の偏導関数を含むうえに消散項までついているからな。次は境界条件について見ていこう。
境界条件
波動方程式の境界値問題を解く際の境界条件として、ここでは固定端条件、自由端条件、無反射条件の3種類を考えます。
固定端条件とは、境界部分における波の高さが固定されている条件です。物理例としては、太鼓の膜の振動などがこれに当たります。
自由端条件とは、境界部分における波の高さが固定されておらず、かつ、境界部分で波の反射も起きる条件です。 物理例としては、水を張ったバケツの水面に振動を与えたときの水面波などが考えられます。
無反射条件とは、境界部分における波の反射が起こらない条件です。この条件は、広範囲での波動を想定した計算を行う場合に計算時間を節約するために用いられます。 例えば、非常に大きな湖の中央で水面にボールを落としたときの、ボールを落とした場所付近の水面の様子だけが知りたいとします。このような場合、湖全体の水面を計算することは非常に時間がかかるため、無反射条件を用いてボールを落とした場所付近のみで計算することがあります。
これら3つの境界条件は境界が存在する向きに応じて次のように与えられます。
固定端条件とは、境界部分における波の高さが固定されている条件です。物理例としては、太鼓の膜の振動などがこれに当たります。
自由端条件とは、境界部分における波の高さが固定されておらず、かつ、境界部分で波の反射も起きる条件です。 物理例としては、水を張ったバケツの水面に振動を与えたときの水面波などが考えられます。
無反射条件とは、境界部分における波の反射が起こらない条件です。この条件は、広範囲での波動を想定した計算を行う場合に計算時間を節約するために用いられます。 例えば、非常に大きな湖の中央で水面にボールを落としたときの、ボールを落とした場所付近の水面の様子だけが知りたいとします。このような場合、湖全体の水面を計算することは非常に時間がかかるため、無反射条件を用いてボールを落とした場所付近のみで計算することがあります。
これら3つの境界条件は境界が存在する向きに応じて次のように与えられます。
以下それぞれの境界条件について、境界が左側、右側、上側、下側にある場合の式を順に示す。
・固定端条件 \[ \begin{align} u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ \end{align}\] ・自由端条件 \[ \begin{align} u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_{i+1} , y_j , t_{n+1} \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_{i-1} , y_j , t_{n+1} \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_i , y_{j+1} , t_{n+1} \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_i , y_{j-1} , t_{n+1} \right) \\\\ \end{align}\] ・無反射条件 \[ \begin{align} u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i+1} , y_j , t_n \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i-1} , y_j , t_n \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i} , y_{j+1} , t_n \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i} , y_{j-1} , t_n \right) \\\\ \end{align}\]
・固定端条件 \[ \begin{align} u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ u \left( x_i , y_j , t_{n+1} \right) &= 0 \\\\ \end{align}\] ・自由端条件 \[ \begin{align} u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_{i+1} , y_j , t_{n+1} \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_{i-1} , y_j , t_{n+1} \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_i , y_{j+1} , t_{n+1} \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= u \left( x_i , y_{j-1} , t_{n+1} \right) \\\\ \end{align}\] ・無反射条件 \[ \begin{align} u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i+1} , y_j , t_n \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i-1} , y_j , t_n \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i} , y_{j+1} , t_n \right) \\\\ u \left( x_i , y_j , t_{n+1} \right) &= \left( 1 - \frac{c \Delta t}{h} \right) u \left( x_{i} , y_j , t_n \right) + \frac{c \Delta t}{h} u \left( x_{i} , y_{j-1} , t_n \right) \\\\ \end{align}\]
ナユミ
陽的公式と境界条件の式がそろったから、あとは初期条件かしら？
カヤ
そうだな。初期条件と計算途中での振動を与える分布関数について説明しておこう。
振動の分布関数
消散型波動方程式の陽的公式は時刻 \( t_n \) と \( t_{n-1} \) における \( u \) の値から、時刻 \( t_{n+1} \) における \( u \) の値を求める式です。
そのため、陽的公式による計算をする前に、時刻 \( t_n \) と \( t_{n-1} \) における \( u \) の値に振動による波形を加算しておけば、振動子の効果を表現できます。
ここでは、次の関数を用いて振動子の効果を表現します。
\[ 振動の分布関数 \omega \]
\[ \omega \left( x_i,y_j \right) = Ae^{- \alpha \left( x_i - o_x \right) ^2} e^{- \alpha \left( y_j -
o_y \right) ^2}\]
\( A \) ：分布関数の最大値
\( \alpha \) ：分布関数の裾野の広がり
\( o_x \) ：振動子の \( x \) 座標
\( o_y \) ：振動子の \( y \) 座標
\( \alpha \) ：分布関数の裾野の広がり
\( o_x \) ：振動子の \( x \) 座標
\( o_y \) ：振動子の \( y \) 座標
この関数はガウス型の関数とも呼ばれる関数で、\( o_x \) 、\( o_y \) を中心とする釣鐘状の曲面です。
この関数を周期 \( \tau \) で空間領域全体にわたって \( u \left( x_i , y_j , t_{n} \right) \) と \( u \left( x_i , y_j , t_{n-1}
\right) \) に加えることで振動子の効果を表現します。
なお、冒頭のシミュレータでは \( \alpha \) については振動子1と2で共通とし、\( A \) 、\( o_x \) 、\( o_y \) 、\( \tau \) については振動子1と2で個別に与えています。
なお、冒頭のシミュレータでは \( \alpha \) については振動子1と2で共通とし、\( A \) 、\( o_x \) 、\( o_y \) 、\( \tau \) については振動子1と2で個別に与えています。
ナユミ
これで初期条件についてもわかったから、数値積分ができるわね。
カヤ
そうだな。実際の計算例をいくつか見て、波動方程式の解の性質について簡単にではあるが調べてみよう。
計算例
いくつかの計算例を通じて、2次元消散型波動方程式の性質について見ていきます。
まずは、位相速度 \( c \) についてです。 \( c \) と波が進む速さの関係を調べるため、計算領域の中央で発生した波が四方の境界に到達した時刻 \( T \) を異なる6つの \( c \) について各々測定しプロットしてみました。 なお、\( c \) 以外のパラメータは冒頭のシミュレータのセット「デモ2」のものを使っています。
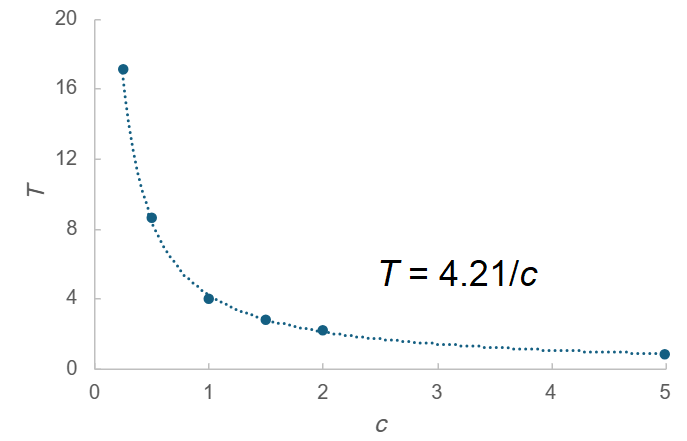
まずは、位相速度 \( c \) についてです。 \( c \) と波が進む速さの関係を調べるため、計算領域の中央で発生した波が四方の境界に到達した時刻 \( T \) を異なる6つの \( c \) について各々測定しプロットしてみました。 なお、\( c \) 以外のパラメータは冒頭のシミュレータのセット「デモ2」のものを使っています。
プロットした点は反比例の式でよく近似できることから、位相速度 \( c \) は波の移動速度と比例関係にあると予想できます。
次に、波の屈折について見ていきます。冒頭のシミュレータのセット「屈折」でシミュレーションを行うと、下図のような波の屈折模様が現れます。 上側の相と下側の相のそれぞれで波面に垂直な直線を引き、これが2つの相の境界線と直角に交わる直線となす角を屈折角と呼びます。 2つの屈折角の間には次のスネルの法則が成り立つことが知られています。
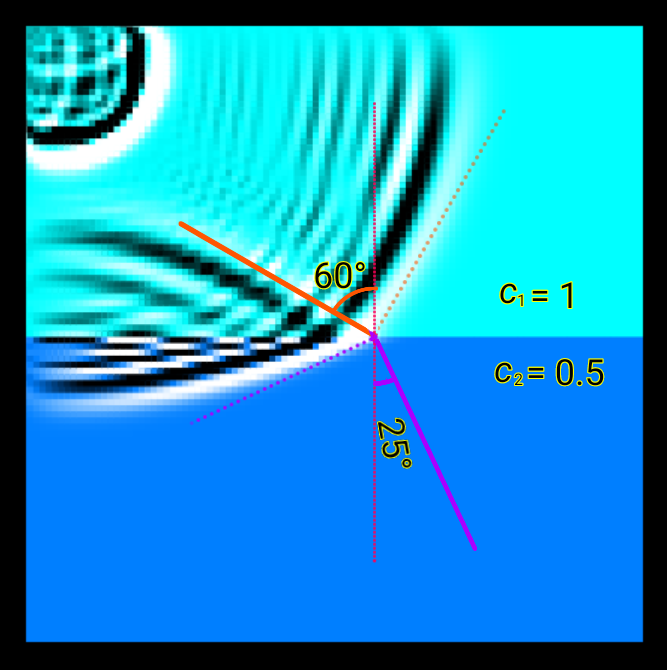
次に、波の屈折について見ていきます。冒頭のシミュレータのセット「屈折」でシミュレーションを行うと、下図のような波の屈折模様が現れます。 上側の相と下側の相のそれぞれで波面に垂直な直線を引き、これが2つの相の境界線と直角に交わる直線となす角を屈折角と呼びます。 2つの屈折角の間には次のスネルの法則が成り立つことが知られています。
\[ スネルの法則\]
\[ \frac{c_1}{c_2} = \frac{\sin \theta _1}{\sin \theta _2} \]
\( c _1 \) ：第1相の位相速度
\( c _2 \) ：第2相の位相速度
\( \theta _1 \) ：第1相の屈折角
\( \theta _2 \) ：第2相の屈折角
\( c _2 \) ：第2相の位相速度
\( \theta _1 \) ：第1相の屈折角
\( \theta _2 \) ：第2相の屈折角
計算結果から目視で測定した第1相の屈折角は60°、第2相の屈折角は25°であり、スネルの法則の右辺に代入すると、
\[ \frac{\sin 60 ^{\circ} }{\sin 25 ^{\circ} } \approx 2.05 \]
となり、\( c_1 / c_2 = 1 / 0.5 = 2 \) と近い値になっていることがわかります。
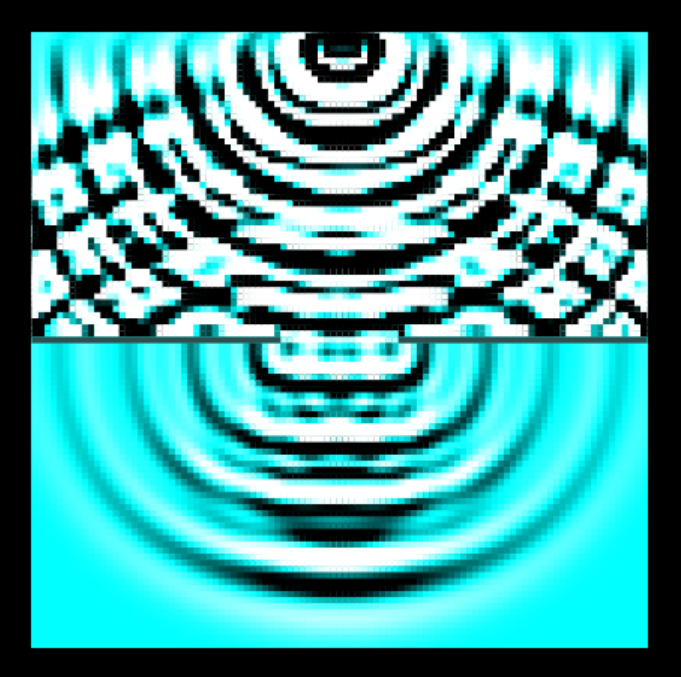
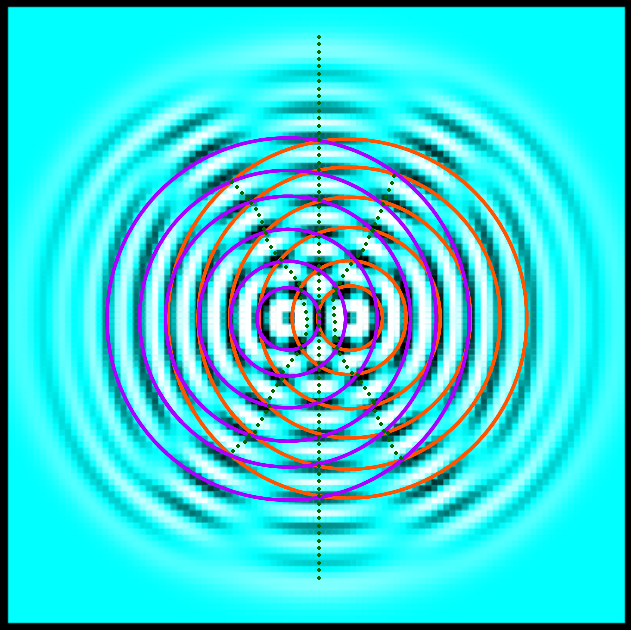
続いて、波の干渉についてです。冒頭のシミュレータのセット「干渉」でシミュレーションを行うと、下図のような波の干渉模様が現れます。
2つの振動子を中心に波面をなぞると、同じ半径の円が左右に順々に並びます。
干渉の縞模様はこれらの左右の円が交わる点に現れ、この場所では2つの振動子から来た波が強め合っています。
逆に、縞模様と縞模様の間の空白部分は2つの振動子から来た波が弱め合っています。
次に、波の回折についてです。
冒頭のシミュレータのセット「回折」でシミュレーションを行うと、左下図のような波の回折が見れます。
なお、回折とは反射や屈折でない方法で波が曲げられることを指します。
右下図は左下図の計算条件からスリット幅だけを広くしたものです。
スリットとの境目以外は、スリット上側からやってきた波がそのまま直進し、全体として縦方向につぶれたような波面になっています。
最後に、消散項の効果について触れておきます。
2次元消散型波動方程式を改めて書き下してみます。
\[ \frac{\partial ^2 u}{\partial t^2} = c^2 \left( \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2
u}{\partial y^2} \right) - p \frac{\partial u}{\partial t} \]
この式の左辺は波の加速度を表しています。
一方、右辺の消散項は波の速度である \( \partial u / \partial t \) に \( -p \) をかけたものになっています。
減衰係数 \( p \) は正の実数なので、消散項は波の速度が正のときは加速度にマイナスを与え、波の速度が負のときは加速度にプラスを与えます。
そのため、減衰係数が大きいほど、波は速やかに消失していく（波の高さが0に近づく）ことになります。
ちなみに、消散項の形式は、ニュートンの運動方程式において空気抵抗を表現する粘性抵抗と同様のものです。
ナユミ
波には色々な性質があって、波動方程式を通じてそれらを調べられるのね。
カヤ
ここで扱った波動方程式では表現できない波動現象ももちろんあるが、高校物理で習うような現象については今回の偏微分方程式で十分かな。
参考：
[1] 原田隆典・本橋英樹、差分法の基礎と応用 ～地震動・波動場や弾性振動解析～、2022年、https://miyazaki-u.repo.nii.ac.jp/records/6575、2024年3月4日閲覧
[2] Robert Clayton and Björn Engquist、ABSORBING BOUNDARY CONDITIONS FOR ACOUSTIC AND ELASTIC WAVE
EQUATIONS、Bulletin of the Seismological Society of America、Vol.67、No.6、p1529-1540、1977年
[3] Wikipedia 波動方程式、https://ja.wikipedia.org/wiki/波動方程式、2024年3月4日閲覧
[4] 西原健二、消散型波動方程式のコーシー問題の解の拡散現象、日本数学会、数学、62巻、2号、p164-181、2010年
[5] 渡辺朋成、消散型波動方程式におけるStrichartz型評価とその応用、第11回数学総合若手研究集会、https://www.math.sci.hokudai.ac.jp/sympo/mcyr/2015/abst.html、2024年3月5日閲覧
[6] 和達三樹、物理のための数学 （物理入門コース10）、岩波書店、1983年3月14日発行
[7] 日野原伸生、計算物理学２ 講義資料 第14回：微分方程式の解法その４、https://wwwnucl.ph.tsukuba.ac.jp/~hinohara/compphys2-18/、2024年3月7日閲覧
[8] Paul G.Hewitt／John Suchocki／Leslie A.Hewitt 著、 小出昭一郎 監修／黒星瑩一 訳、物理科学のコンセプト３ 流体と音波、共立出版、1997年8月15日発行
[9] Paul G.Hewitt／John Suchocki／Leslie A.Hewitt 著、 小出昭一郎 監修／本田 建 訳、物理科学のコンセプト４ 電気・磁気と光、共立出版、1997年11月1日発行
前の記事
第17話
拡散律速凝集(DLA)
拡散律速凝集(DLA)
次の記事
第19話
ブランコと振り子
ブランコと振り子