第23話  陽的差分法

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 5話、 6話、 9話、 14話、 21話、 22話

　陽的差分法は時刻 \( t \) を変数に持つ偏微分方程式の数値積分法の一つです。 偏微分方程式の数値積分法の中では、最も基本的な部類に入ります。 以下では、1次元の拡散方程式を通じて、陽的差分法の解説をしていきます。

　ここで問題にしている1次元拡散方程式は位置 \( x \) と時刻 \( t \) の2変数関数である \( c \left( x, t \right) \) についての偏微分方程式です。 \( c \) の時間発展を陽的差分法によって求めることがここでの目的になります。
　初期条件とは常微分方程式の時と同じく、時刻 \( t = 0 \) における未知関数の値を指します。 ここでは、両端を除く \( x \) の定義域全体で \( c = 0 \) としました。
　境界条件とは、\( x \) の定義域の両端における \( c \) の条件です。 左端 \( \left( x = 0 \right) \) においては任意の時刻で \( c = 0 \) としました。 このように未知関数の値を直接指定する境界条件は第1の型の境界条件と呼ばれています。 一方、右端 \( \left( x = 1 \right) \) においては任意の時刻で \( {\partial c}/{\partial x} = 0 \) としました。 このように未知関数の位置 \( x \) に関する偏導関数の値を指定する境界条件は第3の型の境界条件と呼ばれています。
　以上のように、初期条件や境界条件を指定して偏微分方程式を解く問題は一般的に境界値問題と呼ばれています。

　差分近似とは導関数を近似する方法のことです。 この方法は端的に言えば、導関数の定義にある極限記号を取り除いて、関数の変化量を小さいが無限小ではない有限な値に置き換えるというものです。 先ほどの1次元拡散方程式と、右端の境界条件は差分近似を用いると次のように表すことができます。

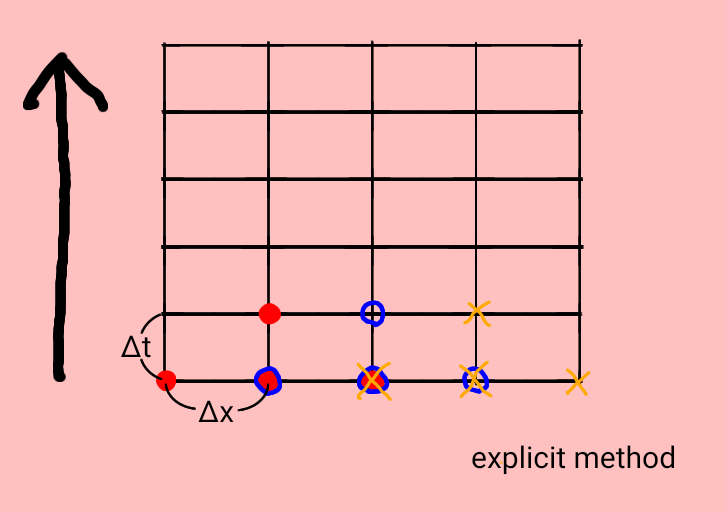
　時刻 \( t \) と位置 \( x \) は元々は連続な実区間として定義されていますが、陽的差分法を適用するにあたりこれらを離散化します。 時刻については \[ t_n = n \Delta t \ \ \ \ \left( n = 0, 1, \ldots \right) \] 位置については \[ x_i = i \Delta x \ \ \ \ \left( i = 0, 1, \ldots , m \right) \] ただし、\( m \Delta x = 1 \) とします。
　これらの条件を、先ほどの差分近似に代入して式変形をすると、差分近似の偏微分方程式から陽的公式が導かれ、右端の \( c \) の値も次式で表すことができます。

　初期条件なども含めて、改めて問題設定を \( x_i \) 、\( t_n \) の式として書き下すと次のようになります。

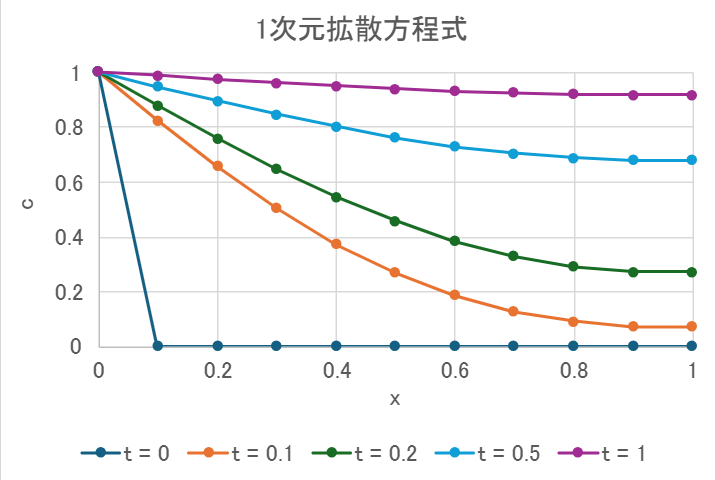
　上図は、\( \Delta x = 0.1 \) 、\( \Delta t = 0.001 \) として先ほどの問題を数値計算した結果です。 時刻 \( t \) が進むにつれて、空間全体で \( c \) の値が左端の値1に近づいていく様子が読み取れます。