目次
・集合
カヤ
今回は集合について解説しよう。
集合
ナユミ
集合？集合時間のこと？
カヤ
いや、「集まる」という動的な視点ではなくて、「集まり」という固定された視点だな。
\[ 集合の定義\]
\[ 範囲のはっきりした「ものの集まり」のことを \boldsymbol {集合} と呼ぶ。\]
ナユミ
はあ、まあ、そうなのね。
カヤ
まあ、そうなんだ。次に、個々の「もの」がある集合に入っているかいないかを次のような記号で定義していく。
\[ 集合の要素\]
1つの集合を形作る個々のものをその集合の要素あるいは元と呼ぶ。\( x \) が集合 \( X \) の元であることを、
\[ x \in X \ \ あるいは \ \ X \ni x \]
と書く。これを、\( x \) が \( X \) に属する、\( x \) は \( X \) に含まれる、\( X \) が \( x \) を含む、等とも言う。一方、\( x \) が \( X \) の元でないことは、
\[ x \notin X \ \ あるいは \ \ X \not\ni x \]
と書く。
ナユミ
ふーん、「麺類」という集合の中に「ラーメン」という元がある、みたいな感じ？
カヤ
まあ、そんな感じだな。続いて、集合を書き表す2通りの方法についてだ。
\[ 集合の記法\]
ある集合のすべての要素を \( a,b,c, \ldots \) というように列挙することができる場合、その集合を
\[ \left\{ a,b,c, \ldots \right\} \]
という記号で表す。これを集合の外延的記法と呼ぶ。一方、ある条件 \( C(x) \) が与えられたとき、その条件を満たす \( x \) 全部の集合を
\[ \left\{ x|C(x) \right\} \]
という記号で表す。この記法を集合の内包的記法と呼ぶ。
ナユミ
中身を1個1個全部書くか、分類だけ書いておくかってことね。
カヤ
そうだな。次に集合をそれに含まれる元の個数で分類することについてだ。
\[ 元の個数による集合の分類\]
有限個の元からなる集合を有限集合と呼び、無限に多くの元を持つ集合を無限集合と呼ぶ。
元を1つも含まない集合を空集合と呼び、記号 \[ \varnothing \] で表す。
元を1つも含まない集合を空集合と呼び、記号 \[ \varnothing \] で表す。
無限集合は現実世界のものを考えると存在しない気がしますが、数学世界の中にはたくさんあります。
例えば、すべての自然数からなる集合は無限集合になりますし、実区間 \( \left[0,1 \right] \) も無限集合です。
ナユミ
そっか。自然数はどこまでも大きな数が取れるし、実区間はその区間の中でいくらでも細かく区切って実数が取れるもんね。
カヤ
そういうことだな。次は、2つの集合同士の関係について、いくつか言葉を定義しよう。
\[ 部分集合\]
\( X \) と \( Y \) を2つの集合とする。\( X \) の任意の元が \( Y \) の元であり、かつ、\( Y \) の任意の元が \( X \) の元であるとき、\( X \) と \( Y \) は等しいと言い、これを
\[ X = Y \]
と表す。
\( X \) の任意の元が \( Y \) の元であるとき、\( X \) は \( Y \) の部分集合である、あるいは \( X \) は \( Y \) に含まれるといい、 \[ X \subset Y \ \ あるいは \ \ Y \supset X \] と書く。これは \( X = Y \) である場合も考慮される。空集合 \( \varnothing \) は任意の集合の部分集合とする。
\( X \) が \( Y \) の部分集合で、\( X = Y \) でないとき、\( X \) は \( Y \) の真部分集合であるという。
\( X \) の任意の元が \( Y \) の元であるとき、\( X \) は \( Y \) の部分集合である、あるいは \( X \) は \( Y \) に含まれるといい、 \[ X \subset Y \ \ あるいは \ \ Y \supset X \] と書く。これは \( X = Y \) である場合も考慮される。空集合 \( \varnothing \) は任意の集合の部分集合とする。
\( X \) が \( Y \) の部分集合で、\( X = Y \) でないとき、\( X \) は \( Y \) の真部分集合であるという。
ナユミ
うん、これは例えば、「東京に住んでいる人」の集合は「日本に住んでいる人」の集合の真部分集合である、みたいな感じね。
カヤ
そんな感じだな。続いて、2つの集合から作られる集合についてだ。
\[ 和集合と共通部分\]
\( X \) と \( Y \) の少なくとも一方の元であるもの全体の集合を、\( X \) と \( Y \) の和集合とよび、記号
\[ X \cup Y \]
で表す。また、\( X \) と \( Y \) の両方の元であるもの全体の集合を、\( X \) と \( Y \) の共通部分とよび、記号
\[ X \cap Y \]
で表す。\( X \cap Y = \varnothing \) であるとき、\( X \) と \( Y \) は交わらないと言い、\( X \cap Y = \varnothing \) でないとき \( X \) と \( Y \) は交わると言う。
ナユミ
ふむ、これは「近畿地方に含まれる都道府県」の集合と「東海地方に含まれる都道府県」の集合を考えるとわかりやすいわね。
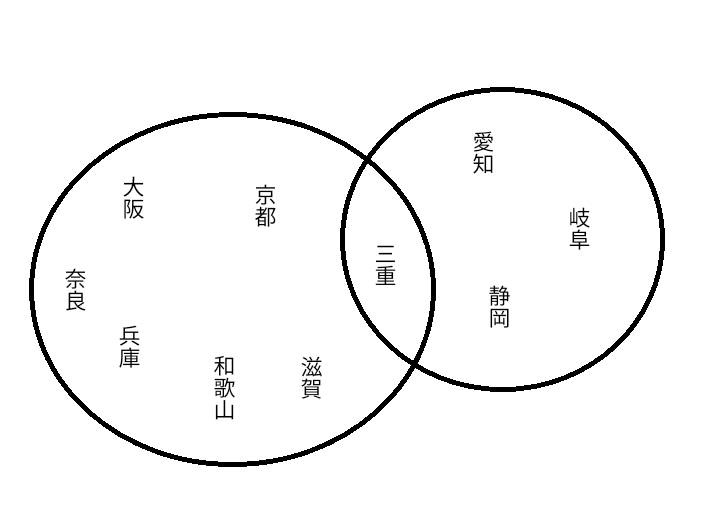
\[ K=\left\{ 大阪府,\ 京都府,\ 兵庫県,\ 奈良県,\ 和歌山県,\ 三重県,\ 滋賀県 \right\}\]
\[ T=\left\{ 愛知県,\ 岐阜県,\ 三重県,\ 静岡県 \right\}\]
\[ K \cup T = \left\{ 大阪府,\ 京都府,\ 兵庫県,\ 奈良県,\ 和歌山県,\ 三重県,\ 滋賀県,\ 愛知県,\ 岐阜県,\ 静岡県\right\}\]
\[ K \cap T = \left\{ 三重県 \right\}\]
カヤ
三重県だけが近畿と東海の両方に属しているということだな。
和集合と共通部分の考え方は2個以上の集合についても適用できます。
そこで、次のようなものを考えておくと便利です。
\[ 集合族\]
「集合の集合」のことを集合族と呼ぶ。\( \Omega \) を1つの集合族とするとき、\( \Omega \) に属する少なくとも1つの集合の元となっているもの全体の集合を「集合族 \( \Omega \) の和集合」と呼び、これを
\[ \bigcup _{X \in \Omega} X \]
と表す。
また、\( \Omega \) に属するすべての集合に共通な元全体の集合を「集合族 \( \Omega \) の共通部分」と呼び、これを
\[ \bigcap _{X \in \Omega} X \]
と表す。
\( \Omega \) は大文字のギリシャ文字で「オメガ」と読みます。
集合の集合とは、例えば \( \Omega \) を「トランプの全種類のカード」とすれば、その中に「ハートのカード」の集合や「スペードのカード」の集合などがあるという話です。
カヤ
それから、集合に番号を付けるときは、次のような方法を使うぞ。
\[ 集合の番号付け\]
添字集合 \( I \) の各元 \( i \) に対し、それぞれ1つの集合 \( X_i \) を対応付けることにより得られる集合族を
\[ \left\{ X_i \right\} _{i \in I} \]
と表す。この集合族の和集合を
\[ \bigcup _{i \in I} X_i \]
で表し、共通部分を
\[ \bigcap _{i \in I} X_i \]
で表す。\( I \) が \( n \) 個の元をもつ有限集合で、その元が \( 1,2, \cdots , n \) と書かれているときには、集合族 \( \left\{ X_i \right\} _{i \in I} \) を
\[ \left\{ X_i \right\} _{i=1,2, \cdots , n} \]
のようにも表し、その和集合を
\[ \bigcup _{i=1} ^n X_i \ \rm または \ \it X \rm _1 \cup \it X \rm _2 \cup \cdots \cup \it X _n \]
と書き、その共通部分を、
\[ \bigcap _{i=1} ^n X_i \ \rm または \ \it X \rm _1 \cap \it X \rm _2 \cap \cdots \cap \it X _n \]
と書く。\( I \) が正の整数全体の集合である場合、集合族 \( \left\{ X_i \right\} _{i \in I} \) の和集合を
\[ \bigcup _{i=1} ^{\infty} X_i \]
と書き、その共通部分を
\[ \bigcap _{i=1} ^{\infty} X_i \]
と書く。
ナユミ
いろいろと表記法があるのね。
カヤ
いろいろな場合があるからな。次は、集合同士の差について考えてみよう。
\[ 集合同士の差\]
\( X \) 、\( Y \) を2つの集合とする。\( Y \) の元であって \( X \) の元でないようなもの全体の集合を \( Y - X \) で表す。特に \( X \subset Y \) である場合には、\( Y - X \) を、\( Y \) に対する \( X \) の補集合と呼ぶ。
考えている集合のすべてが、ある集合 \( U \) の部分集合であるとき、\( U \) を全体集合と呼ぶ。この場合、集合 \( X \) の元でないが、全体集合 \( U \) の元である集合を単に \( X \) の補集合と呼び、 \[ U - X = X^c \] と書く。
考えている集合のすべてが、ある集合 \( U \) の部分集合であるとき、\( U \) を全体集合と呼ぶ。この場合、集合 \( X \) の元でないが、全体集合 \( U \) の元である集合を単に \( X \) の補集合と呼び、 \[ U - X = X^c \] と書く。
これは全体集合 \( U \) を「トランプの全種類のカード」、集合 \( X \) を「ハートのカード」とすれば、補集合 \( X^c \) は「ハートのカード以外のすべてのトランプのカード」になります。
カヤ
次に、補集合についての法則であるド・モルガンの法則を見ておこう。
\[ ド・モルガンの法則\]
補集合に関して、次のド・モルガンの法則が成り立つ。
\[ \left( X \cup Y \right) ^c = X^c \cap Y^c \]
\[ \left( X \cap Y \right) ^c = X^c \cup Y^c \]
上の方は全体集合を「トランプの全種類のカード」にして、 \( X \) を「ハートのカード」、\( Y \) を「絵札」にすれば、「ハートのカードと絵札を合わせたもの」以外のカードは、「ハートのカード」以外のカードと「絵札」以外のカードとの重複部分に等しいということです。
下の方は逆に、「ハートの絵札」以外のカードは、「ハートのカード」以外のカードと「絵札」以外のカードとを合わせたものに等しいということです。
下の方は逆に、「ハートの絵札」以外のカードは、「ハートのカード」以外のカードと「絵札」以外のカードとを合わせたものに等しいということです。
カヤ
次に、べき集合というものについて少し触れておこう。
\[ べき集合\]
部分集合全体の集合をべき集合と呼ぶ。集合 \( U \) のべき集合を \( \mathcal P \rm ( \it U \rm ) \) と表す。
ナユミ
\( \mathcal P \) ってちょっとおしゃれね。
カヤ
これは筆記体のPだな。
ナユミ
筆記体かあ。中学の英語でちょっと練習したわね。
カヤ
そうだな。ところで、べき集合については大丈夫か？
ナユミ
そうね、部分集合全部の集合だから、例えば集合 \( U \) を
\[ U = \left\{ 〇,\ ×\right\}\]
にしたらこうなるかしら。
\[ \mathcal P \rm ( \it U \rm ) = \left\{ \left\{ 〇,\ ×\right\} ,\ \left\{ 〇\right\}, \ \left\{ ×\right\}, \varnothing \right\}\]
もとの集合が有限集合の場合、べき集合の元の個数はもとの集合の元の個数を \( x \) とすれば \( 2^x \) になります。
これは \( x \) 個の各々の元があるかないかで場合分けができるためです。
カヤ
次に、集合同士を組にする直積について定義しておこう。
\[ 直積 \]
有限集合 \( I = \left\{ 1,\ 2,\ \cdots ,\ n \right\} \) を添字集合とする集合族 \( \left\{ X_i \right\} _{i=1,2, \cdots , n} \) が与えられたとする。そのとき、各 \( X_i \) からそれぞれ1つの元 \( x_i \) をとって、順序付けられた組
\[ \left( x_1 , \ x_2 , \ \cdots , \ x_n \right) \]
を作り、そのような組全体の集合を \( \left\{ X_i \right\} _{i=1,2, \cdots , n} \) の直積（または \( X_1 , \ X_2 , \cdots , \ X_n \) の直積）と呼ぶ。これを、
\[ X_1 \times X_2 \times \cdots \times X_n \ \ \rm または \ \ \it \prod ^n _{i \rm =1} \it X_i \]
で表す。
直積 \( Z = X_1 \times X_2 \times \cdots \times X_n \) の元 \( z = \left( x_1 , \ x_2 , \ \cdots , \ x_n \right) \) に対し、\( x_i \) はその \( X_i \) 成分または第 \( i \) 成分と呼ばれる。成分の代わりに座標という言葉を用いることもある。
直積 \( Z = X_1 \times X_2 \times \cdots \times X_n \) の元 \( z = \left( x_1 , \ x_2 , \ \cdots , \ x_n \right) \) に対し、\( x_i \) はその \( X_i \) 成分または第 \( i \) 成分と呼ばれる。成分の代わりに座標という言葉を用いることもある。
具体例を挙げると、
\[ X_1 = \left\{ ご飯, \ パン\right\} \]
\[ X_2 = \left\{ 魚, \ チキン\right\} \]
とすると、\( Z = X_1 \times X_2 \) の元は
\( \left( ご飯, \ 魚\right)\) 、
\( \left( ご飯, \ チキン\right)\) 、
\( \left( パン, \ 魚\right)\) 、
\( \left( パン, \ チキン\right)\)
の4つになります。
カヤ
最後に、集合に含まれる元の個数についての言葉を定義しておこう。
\[ 有限集合の濃度\]
有限集合 \( X \) に対して、その元の個数を \( X \) の濃度と言い、
\[ |X| \]
と書く。\( X \) と \( Y \) を有限集合とすると、濃度について、次が成り立つ。
\[ |X \cup Y| = |X| + |Y| - |X \cap Y |\]
先ほどの都道府県の話で考えると、近畿・東海合わせた都道府県の数 \( |K \cup T| \) は、近畿が7、東海が4、両方に属しているのが三重県だけで1なので、
\[ |K \cup T| = 7 + 4 - 1 = 10\]
となります。三重県だけ2回カウントしているため、1個余分を引いておく形です。
ナユミ
……勢いでここまで話についてきたけど、これって何に使うの？
カヤ
集合は今後説明する「確率」の話に出てくるから、今回先に説明しておいたんだ。
ナユミ
そうなんだ。覚えておくわ。
参考：
[1] 松坂和夫、現代数学序説 ──集合と代数、筑摩書房、2017年12月6日発行
前の記事
第13話
定積分
定積分
次の記事
第15話
順列・組合せ・二項定理
順列・組合せ・二項定理