目次
・順列
・組合せ
・同じものを含む順列
・二項定理と多項定理
カヤ
今回は物の数え上げに関係した概念である順列と組合せ、それらの応用である二項定理と多項定理について解説しよう。まずは順列から。
順列
ナユミ
順列？順番に列に並んでくださいってことかな？
カヤ
まあ、そういうことだな。次のような記号を使うんだな。
異なる \( n \) 個のものから \( r \) 個を取り出して1列に並べたものを、\( n \) 個から \( r \) 個とる順列と呼び、その総数を \( _n \rm P _ \it r \) で表す。
\( \rm P \) はPermutation（順列）の略です。
順列の総数 \( _n \rm P _ \it r \) は次の計算式で求められます。
\[ _n \rm P _ \it r \rm = \it n \rm( \it n \rm -1)( \it n \rm -2) \cdots ( \it n \rm - \it r \rm + 1) \]
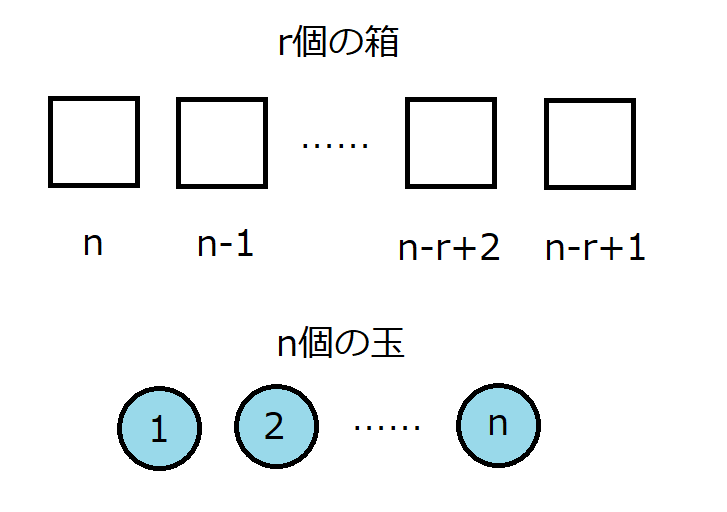
これは番号が振られた \( n \) 個の玉を \( r \) 個の箱に左から順に入れるときのパターン数を考えるとわかりやすいです。
1番左の箱に玉を入れるときは、\( n \) 個の玉から1個を選ぶから \( n \) 通り、左から2番目の箱に玉を入れるときは残りの \( n-1 \) 個の玉から1個を選ぶから \( n-1 \) 通り、以下同様に繰り返していくと上の式が導かれます。
なお、足し算ではなくかけ算の計算になるのは、
それぞれの箱に入れる玉を選ぶ選択肢1つ1つに対して、次の箱に入れる玉を選ぶ選択肢が考えられるからです。
例えば \( n = 3 \) 、\( r = 2 \) の場合
\[ _3 \rm P _ 2 = 3 \times 2 = 6 \]
通りとなり、下図のようになります。
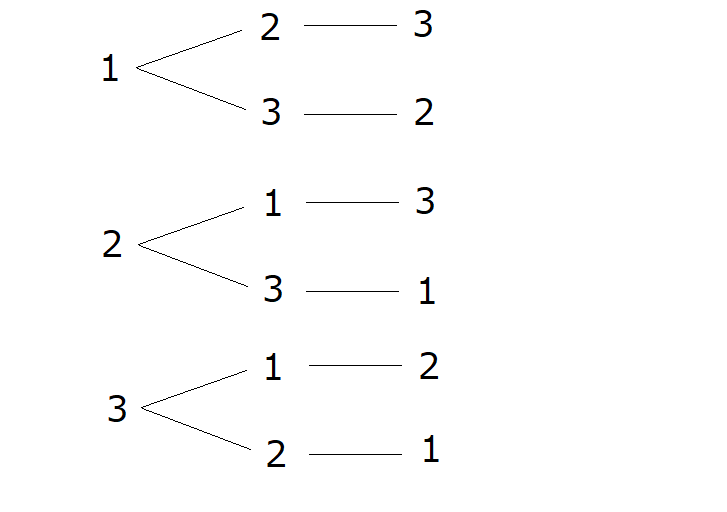
このような図を「樹形図」と呼びます。
ナユミ
樹形図かあ。言われてみれば木の枝が広がっていくみたいな感じね。
カヤ
そうだな。それと、順列の総数は階乗を使うともっとシンプルに書ける。
階乗は指定した自然数以下の自然数をすべて掛け合わせたものです。
すなわち、\( n \) の階乗 \( n! \) は次式で表されます。
\[ n! = n(n-1)(n-2) \cdots 3 \cdot 2 \cdot 1 \]
ナユミ
びっくりマークが階乗の記号なのね！なんだか面白いわね！
カヤ
そうだな！それと、\( 0! = 1 \) と定義するぞ！
ナユミ
どうして？
カヤ
そうするといろいろと都合がいいからだ。例えばこんなところとか。
\[ \begin{align}
3! &= 3 \cdot 2 \cdot 1 \\\\
2! &= 2 \cdot 1 = \frac{3!}{3} \\\\
1! &= 1 = \frac{2!}{2} \\\\
0! &= 1 = \frac{1!}{1}
\end{align}\]
\[ n! = \frac{(n+1)!}{n+1} \]
の関係を \( n=0 \) でも成り立たせるには、\( 0! = 1 \) とすると都合がいいです。
階乗を使うと順列の総数の式は次のように書けます。
\[ \begin{align}
_n \rm P _ \it r &= \it n \rm( \it n \rm -1)( \it n \rm -2) \cdots ( \it n \rm - \it r \rm + 1) \\\\
&= \frac{\it n \rm( \it n \rm -1)( \it n \rm -2) \cdots 1}{\rm ( \it n-r \rm ) \rm( \it n-r \rm -1) \rm ( \it n-r \rm -2) \cdots 1} \\\\
&= \frac{\it n \rm !}{\rm \left( \it n \rm - \it r \rm \right) !}
\end{align}\]
ナユミ
2行目を約分すると1行目になってるのね。
カヤ
そうだな。じゃあ次は組合せについてだ。
組合せ
ナユミ
組合せは組合せ？
カヤ
まあそうだが、定義を書いておこう。
異なる \( n \) 個のものから \( r \) 個を取り出して1組としたものを、\( n \) 個から \( r \) 個とる組合せと呼び、その総数を \( _n \rm C \it _r \) で表す。
ナユミ
これは席替えをした後に、席の近い4人で班分けしたときの状況ね。
カヤ
その場合だったら、例えばクラスの人数が40人だったら、自分と同じ班になる3人を選ぶ組合せの総数は、\( _{39} \rm C _3 \) になるな。
ナユミ
自分を除いた39人から3人が決まるのね。この組合せの総数はどう計算したらいいのかしら？
順列は異なる \( n \) 個のものから \( r \) 個を取り出して1列に並べたものでした。
組合せは、順列の操作から「1列に並べる」という操作を取り除いたものだと考えることができるため、
順列の総数の公式を「 \( r \) 個のものを1列に並べるパターンの総数」で割れば組合せの総数の公式になります。
「 \( r \) 個のものを1列に並べるパターンの総数」は、「 異なる \( r \) 個のものから \( r \) 個を取り出して1列に並べたものの総数」とも言えるため、これは、 \[ _r \rm P _ \it r \rm = \frac{\it r \rm !}{\rm \left( \it r \rm - \it r \rm \right) !} \rm = \frac{\it r \rm !}{0!}= \it r \rm !\] となります。よって、組合せの総数の公式は次式で表せます。
「 \( r \) 個のものを1列に並べるパターンの総数」は、「 異なる \( r \) 個のものから \( r \) 個を取り出して1列に並べたものの総数」とも言えるため、これは、 \[ _r \rm P _ \it r \rm = \frac{\it r \rm !}{\rm \left( \it r \rm - \it r \rm \right) !} \rm = \frac{\it r \rm !}{0!}= \it r \rm !\] となります。よって、組合せの総数の公式は次式で表せます。
\[ \begin{align}
_n \rm C \it _r &= \frac{_n \rm P \it _r}{r!} \\\\
&= \frac{n!}{r!(n-r)!}
\end{align}\]
実際に計算するときは、1行目の
\[ \frac{_n \rm P \it _r}{r!} \]
を使った方が階乗の計算が少なく楽です。
また、\( n \) 個から \( r \) 個とる組合せの総数は、\( n \) 個から \( n-r \) 個とる組合せの総数に等しいため、 \[ _n \rm C \it _r \rm = {} \it _n \rm C \it _{n-r} \] が成り立っています。これは、グループの片側を決めれば、もう片方はおのずと決まるということからわかります。
また、\( n \) 個から \( r \) 個とる組合せの総数は、\( n \) 個から \( n-r \) 個とる組合せの総数に等しいため、 \[ _n \rm C \it _r \rm = {} \it _n \rm C \it _{n-r} \] が成り立っています。これは、グループの片側を決めれば、もう片方はおのずと決まるということからわかります。
ナユミ
よし、じゃあ練習にさっきのクラスの班の組合せの総数を計算してみるわ。
\[ _{39} \rm C _3 = \frac{39 \cdot 38 \cdot 37}{3 \cdot 2 \cdot 1} = 9139\]
ナユミ
9139通りの中から選ばれた1班なのね、これは仲のいい友達ばかりだったら奇跡を感じちゃうわね。
カヤ
奇跡はちょっと言いすぎな気もするが、まあそういうことはめったには起こらないだろうな。
ナユミ
良いように言っておけばいいのよ。
カヤ
まあそうだな。じゃあ次に「同じものを含む順列」というものを紹介しておこう。
同じものを含む順列
ナユミ
順列で並べる玉の中に、同じものがあるってことね。
カヤ
そうだな。この場合、同じ玉の並び順については区別しないので、組合せの総数を順列の総数を並び順で割ることで求めたのと同じ要領で、次のようなことを考えることができる。
\[ 同じものを含む順列 \]
\( m \) 種類の文字がすべて合わせて \( n \) 個あり、それらのうち文字 \( L_i \) の個数が \( n_i \) のとき、これらを1列に並べる並べ方の総数は、次式で与えられる。
\[ \frac{n!}{n_1 ! n_2 ! \cdots n_m !} \]
\[ ただし、n = \sum _{i=1} ^m n_i \]
ナユミ
今度は玉じゃなくて文字にしたのね。それはそうと、\( \sum \) って初めて見る記号ね。
カヤ
\( \sum \) は大文字のギリシャ文字で「シグマ」と読む。これは総和記号と呼ばれ、次のような使い方をするんだ。
\[ 総和記号 \sum \]
\( n \lt m \) とする。数列 \( \left\{ a_k \right\} \) を \( a_n \) から \( a_m \) まで足し合わせたものを
\[ \sum _{k=n} ^m a_k\]
と表す。すなわち、
\[ \sum _{k=n} ^m a_k = a_n + a_{n+1} + \cdots + a_{m-1} + a_m \]
である。
先ほどの組合せの総数の式は、この同じものを含む順列の並べ方の総数の公式で、2種類の文字を並べたものと等しくなっています。
\[ _n \rm C \it _r \rm = \frac{\it n \rm !}{\it r \rm ! \rm ( \it n \rm - \it r \rm )!}\]
\[ n = r + (n-r) \]
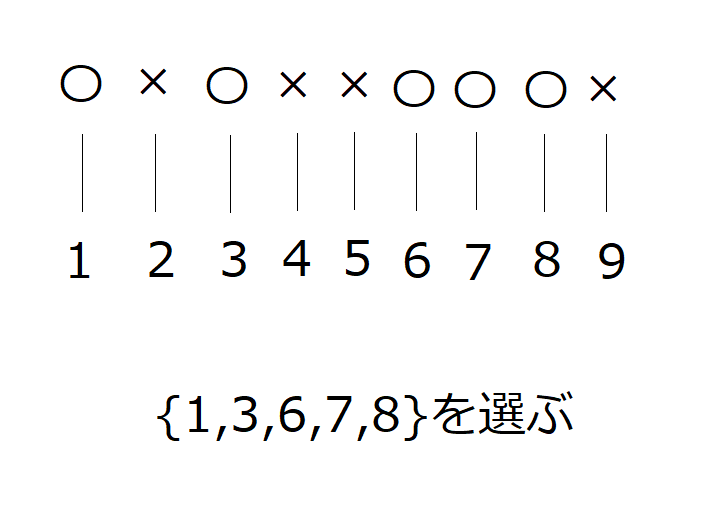
これは、 異なる \( n \) 個のものから \( r \) 個を取り出して1組とするという操作は、「〇」の文字を \( r \) 個、「×」の文字を \( n-r \) 個用意して、これらを1列に並べ、「〇」の文字がある場所と対応したものを選ぶということと同じだからです。
\( _9 \rm C _5 \) を例に図で表すと次のようになります。
ナユミ
そういうことね。よくわかったわ。
カヤ
じゃあ、最後に二項定理と多項定理について紹介しておこう。
二項定理と多項定理
ナユミ
まずは二項定理？からかな。
カヤ
そうだな、二項定理はこういうものだな。
\[ 二項定理\]
\( n \) を自然数とする。次式を二項定理と呼ぶ。
\[ \left( a + b \right) ^n = \sum _{k=0} ^{n} {}_{n} \rm C \it _{k} a^{n-k} b^{k} \]
二項定理の各項の係数を二項係数と呼ぶ。
ナユミ
うーん、綺麗にまとまってるけど、これだけだとよくわからないわ。
カヤ
そうかもな。具体的に、例えば \( n = 3 \) のときを考えてみようか。
\[ \begin{align}
(a+b)^3 &= (a+b)(a+b)(a+b) \\\\
&= (a^2 + 2ab + b^2)(a+b) \\\\
&= a^3 + a^2 b + 2a^2b + 2ab^2 +ab^2 + b^3 \\\\
&= a^3 + 3a^2b + 3ab^2 + b^3 \\\\
&= {}_3 \rm C _0 \it a \rm ^3 + {}_3 \rm C _1 \it a \rm ^2 \it b \rm + {}_3 \rm C _2 \it ab \rm ^2 + {}_3 \rm C _3 \it b \rm ^3
\end{align}\]
ナユミ
うん、ちゃんと成り立ってるわね。けど、どうしてなのかしら？
カヤ
これは、それぞれのかっこにおいて、\( a \) か \( b \) のどちらかを選んで掛けていると考えればいい。そして、3個のかっこから \( b \) を選んだ数で項を分類したということになる。
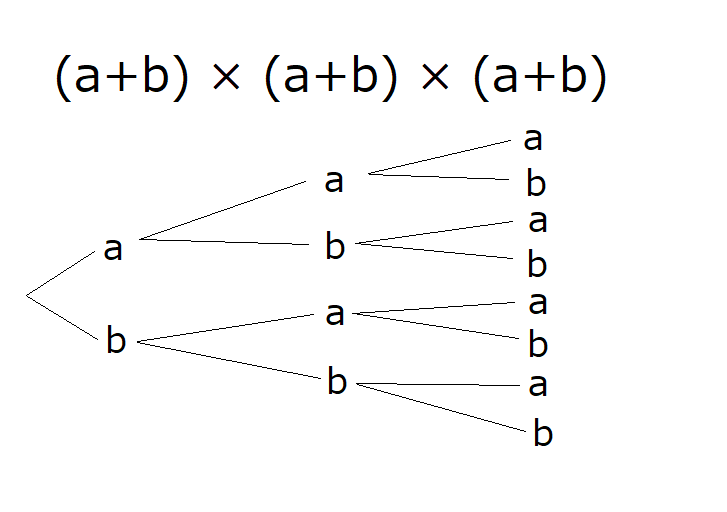
かける順番は関係なく、\( b \) を何回かけたかで項は分類されるので、3個のかっこから \( b \) を選んだかっこの個数が係数に現れています。
この考えを \( n \) に拡張したのが二項定理です。
ナユミ
よくわかったわ。じゃあ、多項定理はどうなるのかしら？
カヤ
多項定理はかっこの中身が2より大きい場合だな。
\[ 多項定理\]
\( n \) を自然数とする。次式を多項定理と呼ぶ。
\[ \left( a_1 + a_2 + \cdots + a_m \right) ^n = \sum _{p_i} \frac{n!}{n_1!n_2! \cdots n_m!} a_1 ^{n_1} a_2 ^{n_2} \cdots a_m ^{n_m} \]
ただし、\( p_i \) は、\( n_1 \geq 0 \) 、\( n_2 \geq 0 \) 、…、\( n_m \geq 0 \) 、\( \sum _{k=1} ^n n_k = n \) であるような整数の組 \( \left( n_1, n_2, \cdots ,n_m \right) \) を表し、右辺の和はそのようなすべての組 \( p_i \) にわたる。
多項定理の各項の係数を多項係数と呼ぶ。
ナユミ
なんだか厳めしい式だけど、要はこれって同じものを含む順列の考えを使っただけよね？
カヤ
そういうことだな。各々の \( a_i \) の指数がかっこのかけ算で \( a_i \) を選んだ回数を表してるから、それが多項係数の分母に来ているということだな。
ナユミ
そうよね。考え方自体はそこまで難しくないけど、実際に計算するとなると大変そうね。
カヤ
まあそうだろうな。今の時代に手計算でやるような計算ではなさそうだな。
ナユミ
コンピュータに感謝しなきゃね。
カヤ
そうだな。
参考：
[1] 宮西正宜 他24名、高等学校 数学A 改訂版、新興出版社啓林館、2008年12月10日発行
[2] 松坂和夫、現代数学序説 ──集合と代数、筑摩書房、2017年12月6日発行
前の記事
第14話
集合
集合
次の記事
第16話
確率
確率