目次
・定積分
・定積分による面積の計算
・変数分離法と定積分
カヤ
今回は定積分について解説しよう。
定積分
ナユミ
定積分？不定積分と何が違うの？
カヤ
不定積分は原始関数の一般的な表記を求める操作だった。一方、定積分はある原始関数に具体的な値を2つ代入してそれらの差を取ったものになる。
\[ 定積分\]
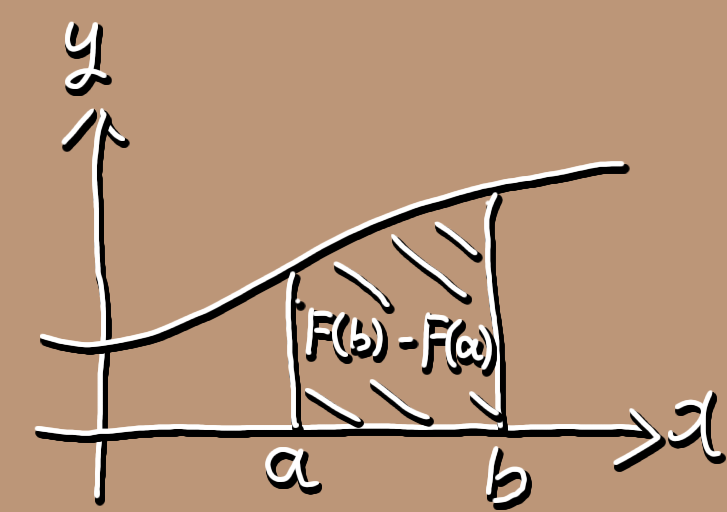
関数 \( f(x) \) の原始関数の1つを \( F(x) \) とする。このとき、\( F(b) - F(a) \) を \( f(x) \) の \( a \) から \( b \)
までの定積分と呼び、
\[ \int ^b _a f(x) dx \]
と表す。ここで、\( a \) をこの定積分の下端、\( b \) を上端と呼ぶ。また、\( F(b) - F(a) \) を \( \left[ F(x) \right] ^b
_a \) と表す。
不定積分で成り立つ公式は定積分でも成り立ちます。
定積分について、以下の公式が成り立つ。
\[ \frac{d}{dx} \int ^x _a f(t)dt = f(x) \ \ \left( a \ \rm は定数 \it \right) \]
\[ \int ^b _a c f(x)dx = c \int ^b _a f(x)dx \ \ \left( c \ \rm は定数 \it \right) \]
\[ \int ^b _a \left\{ f(x) \pm g(x) \right\} dx = \int ^b _a f(x)dx \pm \int ^b _a g(x)dx \]
ナユミ
同じような公式を前にも見た気がするわ。
カヤ
そうだな。定積分の練習も兼ねて、上から順番に証明していこう。
\[ \begin{align}
\frac{d}{dx} \int ^x _a f(t)dt &= \frac{d}{dx} \left[ F(t) \right] ^x _a \\\\
&= \frac{d}{dx} \left( F(x) - F(a) \right) \\\\
&= f(x)
\end{align}\]
カヤ
次は2つめの定数倍の公式。
\[ \begin{align}
\int ^b _a c f(x)dx &= \left[ cF(x) \right] ^b _a \\\\
&= \left( cF(b) - cF(a) \right) \\\\
&= c \left( F(b) - F(a) \right) \\\\
&= c \int ^b _a f(x)dx
\end{align}\]
ナユミ
最後は和と差の公式ね。
\[ \begin{align}
\int ^b _a \left\{ f(x) \pm g(x) \right\} dx &= \left[ F(x) \pm G(x) \right] ^b _a \\\\
&= \left( F(b) \pm G(b) \right) - \left( F(a) \pm G(a) \right) \\\\
&= \left( F(b) - F(a) \right) \pm \left( G(b) - G(a) \right) \\\\
&= \int ^b _a f(x)dx \pm \int ^b _a g(x)dx
\end{align}\]
カヤ
以上、3つの公式は不定積分でも成り立っていたものだが、定積分らしい公式として次の3つがある。
定積分について、以下の公式が成り立つ。
\[ \int ^a _a f(x)dx = 0\]
\[ \int ^b _a f(x)dx = - \int ^a _b f(x)dx\]
\[ \int ^b _a f(x)dx = \int ^c _a f(x)dx + \int ^b _c f(x)dx\]
ナユミ
ふーん、これもすぐに証明できそうね。
カヤ
そうだな。まずは1つめの下端と上端が等しいときの公式。
\[ \int ^a _a f(x)dx = F(a) - F(a) = 0 \]
ナユミ
次は下端と上端がひっくり返ってる公式ね。
\[ \begin{align}
\int ^b _a f(x)dx &= F(b) - F(a) \\\\
&= - \left( F(a) - F(b) \right) \\\\
&= - \int ^a _b f(x)dx
\end{align}\]
カヤ
最後に積分区間を分割する公式。
\[ \begin{align}
\int ^b _a f(x)dx &= F(b) - F(a) \\\\
&= \left( F(c) - F(a) \right) + \left( F(b) - F(c) \right) \\\\
&= \int ^c _a f(x)dx + \int ^b _c f(x)dx
\end{align}\]
カヤ
それから、置換積分も定積分でも成り立つ。
\[ 置換積分\]
\( x = g(u) \) が微分可能で、\( a = g \left( \alpha \right) \) 、\( b = g \left( \beta \right) \) ならば次の式が成り立つ。
\[ \begin{align}
\int _a ^b f(x) dx = \int _{\alpha} ^{\beta} f \left( g \left( u \right) \right) g'(u) du
\end{align}\]
証明は次の通りです。
\( x = g(u) \) とおく。
\[ \begin{align}
\int _{\alpha} ^{\beta} f \left( g \left( u \right) \right) g'(u) du &= \left[ F \left( g \left( u
\right) \right) \right] _{\alpha} ^{\beta} \\\\
&= F \left( g \left( \beta \right) \right) - F \left( g \left( \alpha \right) \right) \\\\
&= F \left( b \right) - F \left( a \right) \\\\
&= \int _a ^b f(x)dx
\end{align}\]
ナユミ
部分積分も、かな？
\[ 部分積分\]
\( f(x) \) 、\( g(x) \) がともに微分可能ならば次の式が成り立つ。
\[ \begin{align}
\int _a ^b f(x) g'(x) dx = \left[f(x)g(x) \right] ^b _a - \int _a ^b f'(x) g(x) dx
\end{align}\]
証明は次の通りです。
\[ \begin{align}
\int _a ^b f(x) g'(x) dx + \int _a ^b f'(x) g(x) dx &= \int _a ^b \left\{ f(x) g'(x) + f'(x) g(x) \right\} dx \\\\
&= \int _a ^b \left\{ f(x) g(x) \right\}' dx \\\\
&= \left[f(x)g(x) \right] ^b _a
\end{align}\]
よって、
\[ \begin{align}
\int _a ^b f(x) g'(x) dx = \left[f(x)g(x) \right] ^b _a - \int _a ^b f'(x) g(x) dx
\end{align}\]
カヤ
じゃあ次は、定積分を使って面積を求めてみよう。
定積分による面積の計算
ナユミ
面積って正方形の面積とかの面積よね？
カヤ
そう、その面積だな。定積分を用いると、 \( xy \) 座標平面上で2つの関数と \( y \) 軸に平行な2直線で囲まれた部分の面積を求めることができる。
まずは、実区間 \( \left[ a,b \right] \) で、\( f(x) \geq 0 \) のときに、\( y = f(x) \) のグラフと \( x \) 軸および2直線 \( x = a \)
、\( x = t \ \left( a \leq t \leq b \right) \) で囲まれた部分の面積 \( S(t) \) を求めてみます。
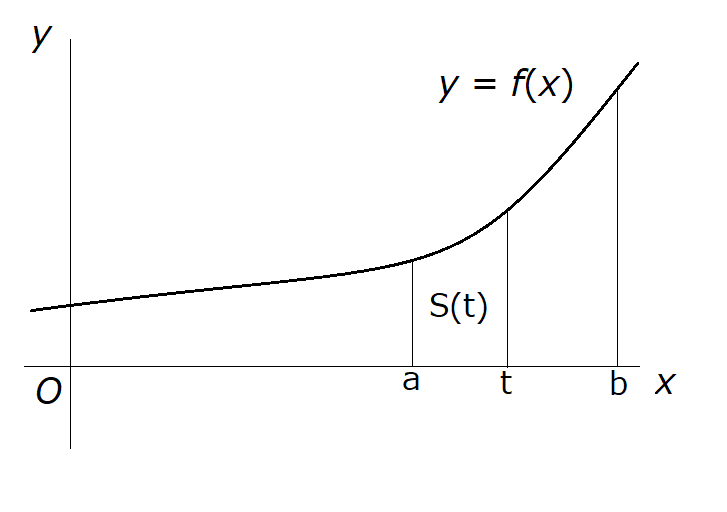
\( x \) が \( t \) から \( t + h \) まで変化したときの面積の変化量
\[ S(t+h) - S(h) \]
について考えます。
これは \( y = f(x) \) のグラフと \( x \) 軸および2直線 \( x = t \) 、\( x = t + h \) で囲まれた部分の面積ですが、
実区間 \( \left[ t,t+h \right] \) の上側にこの面積と同じ大きさの面積を持つ長方形を作ることができます。
この長方形は下図のように、水色で塗ってある2つの部分の面積が等しくなるように長方形の上側の辺を定めれば作れます。
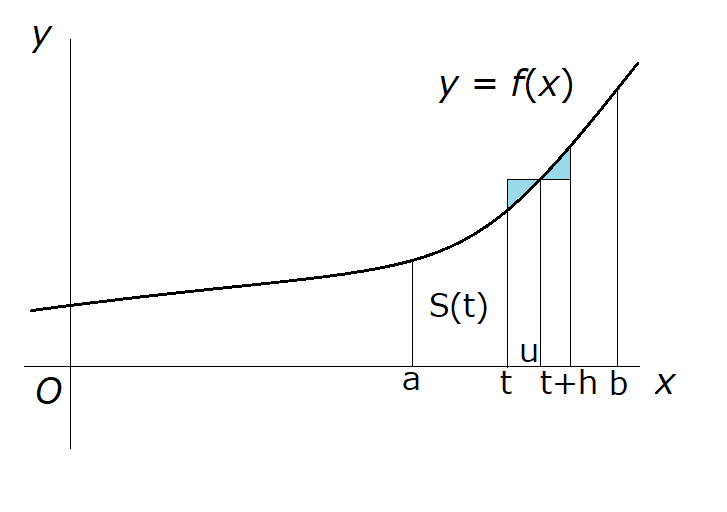
長方形の上側の辺は必ず曲線 \( y = f(x) \) と交わるため、その交点の \( x \) 座標を \( u \) とすれば、長方形の高さは \( f(u) \) で与えられます。
よって、面積の変化量と長方形の面積が等しいことから、次式が成り立ちます。
\[ \begin{align}
S(t+h) - S(h) &= f(u)h \\\\
\frac{S(t+h) - S(h)}{h} &= f(u)
\end{align}\]
ナユミ
ちょっと微分係数っぽくなってきたわね。
カヤ
いい読みだな。ここで、\( h \to 0 \) の極限をとれば、\( u \to t \) となるから、次が成り立つ。
\[ \begin{align}
S(t+h) - S(h) &= f(u)h \\\\
\lim _{h \to 0} \frac{S(t+h) - S(h)}{h} &= \lim _{h \to 0} f(u) \\\\
S'(t) &= f(t)
\end{align}\]
\( S(t) \) は \( f(t) \) の原始関数であることがわかりました。
両辺の変数を \( x \ \left( a \leq x \leq b \right) \) に書き換えてから、下端を \( a \) 、上端を \( t \) として \( x \) で定積分すると、\(
S(a) = 0 \) より次式が成り立ちます。
\[ \begin{align}
S'(x) &= f(x) \\\\
\int _a ^t S'(x) dx &= \int _a ^t f(x) dx \\\\
S(t) - S(a) &= \int _a ^t f(x) dx \\\\
S(t) &= \int _a ^t f(x) dx
\end{align}\]
ナユミ
うん、これで \( y = f(x) \) のグラフと \( x \) 軸および2直線 \( x = a \) 、\( x = t \) で囲まれた部分の面積が定積分で表せたのね。
カヤ
そういうことだ。次に、実区間 \( \left[ a,b \right] \) で、\( f(x) \leq 0 \) のときに、同じように面積を求めてみよう。
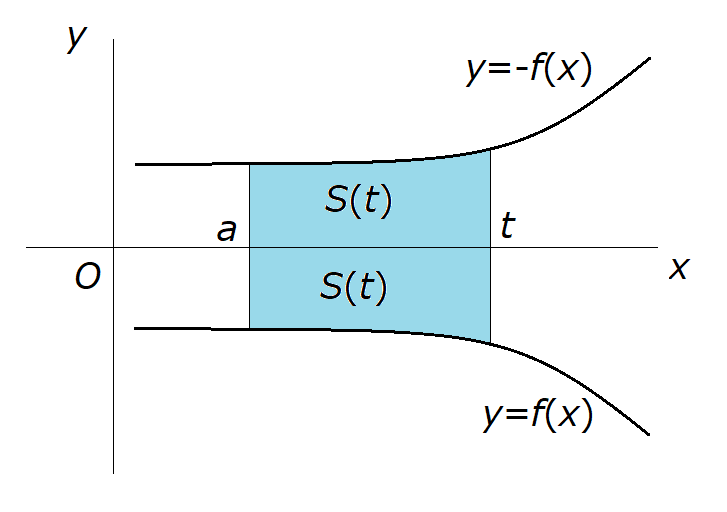
\( f(x) \leq 0 \) の場合、\( y = f(x) \) と \( x \) 軸で線対称な関数 \( y = -f(x) \) にさっきの式を代入すれば同様の議論ができます。
\[ \begin{align}
S(t) &= \int _a ^t \left\{ -f(x) \right\} dx = - \int _a ^t f(x) dx
\end{align}\]
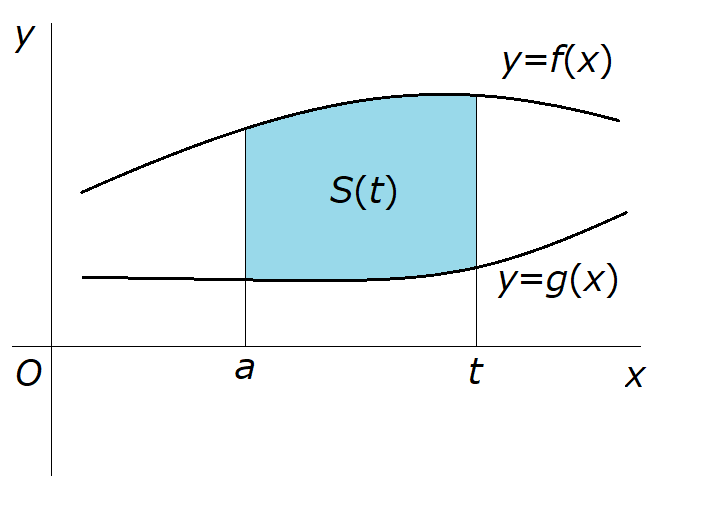
最後に一般的な形として、2つの関数 \( y = f(x) \) 、\( y = g(x) \) が実区間 \( \left[ a,b \right] \) で \( f(x) \geq g(x) \)
を満たすときに、\( y = f(x) \) と \( y = g(x) \) 、および直線 \( x=a \) 、\( x = t \ \left( a \leq t \leq b \right)\)
で囲まれた部分の面積 \( S(t) \) を求めます。
まずは、実区間 \( \left[ a,b \right] \) で \( g(x) \geq 0 \) である場合を考えてみます。
まずは、実区間 \( \left[ a,b \right] \) で \( g(x) \geq 0 \) である場合を考えてみます。
ナユミ
これは、全体から下の部分をくり抜けばいいんじゃないかしら？
カヤ
ナイスアイデアだ。その考えを使えば、\( S(t) \) は次式で表される。
\[ \begin{align}
S(t) &= \int _a ^t f(x) dx - \int _a ^t g(x) dx \\\\
&= \int _a ^t \left\{ f(x) - g(x) \right\} dx
\end{align}\]
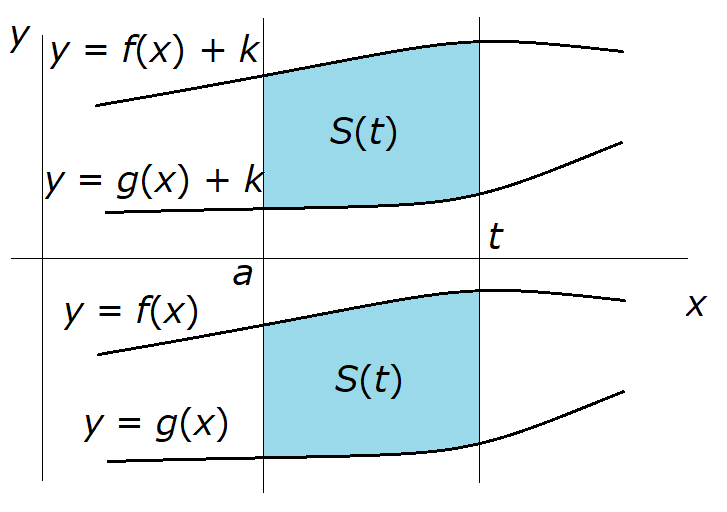
次に、実区間 \( \left[ a,b \right] \) で \( g(x) \lt 0 \) である場合を考えます。
この場合は \( g(x) + k \geq 0 \) を満たす定数 \( k \) を用いて、2つの関数をy軸方向に \( +k \) だけ平行移動した \( y = f(x) + k \) と \( y =
g(x) + k \) について考えても同じことなので、次式が成り立ちます。
\[ \begin{align}
S(t) &= \int _a ^t \left\{ f(x) + k \right\} dx - \int _a ^t \left\{ g(x) + k \right\} dx \\\\
&= \int _a ^t \left\{ f(x) - g(x) \right\} dx
\end{align}\]
ナユミ
結局さっきと同じ式になるのね。
カヤ
そうだな。定積分と面積の話はこれで終わりにして、最後に変数分離法について一つ考察しておこう。
変数分離法と定積分
ナユミ
変数分離法はいつも不定積分を使っていたけど？
カヤ
そうだな。そのいつもの解法についてなんだが、あれは定積分を使っても同じことができる。
不定積分を使って変数分離法を行うときは、初期条件を使って後から積分定数の具体的な値を求めていました。
一方、定積分で変数分離法を行うときは、定積分の下端に初期条件を使って一気に解きます。
両方のやり方を比較するとこうなります。
関数 \( p(x) \) 、\( q(y) \) を含む常微分方程式、
\[ q(y) dy = p(x) dx \]
を2通りの方法で解く。なお、\( p(x) \) 、\( q(y) \) の原始関数をそれぞれ \( P(x) \) 、\( Q(y) \) とし、初期条件は \( \left( x_0, y_0
\right) \) とする。
(1) 不定積分を用いる方法 \[ \begin{align} q(y) dy &= p(x) dx \\\\ \int q(y) dy &= \int p(x) dx \\\\ Q(y) &= P(x) + C \\\\ \end{align}\] 初期条件より、 \[ C = Q(y_0) - P(x_0) \] よって、 \[ \begin{align} Q(y) &= P(x) + Q(y_0) - P(x_0) \\\\ Q(y) - Q(y_0) &= P(x) - P(x_0) \end{align}\]
(2) 定積分を用いる方法 \[ \begin{align} q(y) dy &= p(x) dx \\\\ \int ^y _{y_0} q(y) dy &= \int ^x _{x_0} p(x) dx \\\\ Q(y) - Q(y_0) &= P(x) - P(x_0) \\\\ \end{align}\]
(1) 不定積分を用いる方法 \[ \begin{align} q(y) dy &= p(x) dx \\\\ \int q(y) dy &= \int p(x) dx \\\\ Q(y) &= P(x) + C \\\\ \end{align}\] 初期条件より、 \[ C = Q(y_0) - P(x_0) \] よって、 \[ \begin{align} Q(y) &= P(x) + Q(y_0) - P(x_0) \\\\ Q(y) - Q(y_0) &= P(x) - P(x_0) \end{align}\]
(2) 定積分を用いる方法 \[ \begin{align} q(y) dy &= p(x) dx \\\\ \int ^y _{y_0} q(y) dy &= \int ^x _{x_0} p(x) dx \\\\ Q(y) - Q(y_0) &= P(x) - P(x_0) \\\\ \end{align}\]
ナユミ
本当、どちらの方法でも同じ結果になるのね。定積分を用いる方法のほうが少ない行数で済んでるわね。
カヤ
やってることは同じだがな。今後は定積分を用いた記述も数値実験で使っていくと思う。
ナユミ
わかったわ。
カヤ
それじゃ、今回はここまでにしよう。
参考：
[1] 宮西正宜 他23名、高等学校 数学Ⅱ 改訂版、新興出版社啓林館、2009年12月10日発行
前の記事
第12話
二分法・ニュートン法
二分法・ニュートン法
次の記事
第14話
集合
集合