目次
・不定積分
・様々な関数の不定積分
カヤ
今回は不定積分について解説していこう。
不定積分
ナユミ
不定積分？
カヤ
不定積分は微分の逆操作だな。
ナユミ
微分の逆操作…、関数を微分する前に戻すってことかしら？
カヤ
ああ。それを説明するために、まずは原始関数というものを定義しておこう。
\[ 原始関数\]
関数 \( y = F (x) \) について、 \( \frac{dy}{dx} = f (x) \) となるとき、\( F(x) \) を \( f(x) \) の原始関数という。
\( F'(x) = f(x) \) を満たす関数 \( F(x) \) を原始関数と呼びます。
次の定理も不定積分の理解に役立ちます。
\[ 原始関数についての定理\]
\( F(x) \) 、\( G(x) \) がともに \( f(x) \) の原始関数のとき、
\[ F(x) = G(x) + C \]
を満たすある定数 \( C \) が存在する。
この定理は関数 \( f(x) \) のすべての原始関数は定数を足しただけの差しかないことを意味しています。
この定理を証明するためには、次のことを認める必要があります。
\( f'(x) = 0 \) ならば、\( f(x) = C \) ( \( C \) は任意の定数) である。
\[ 原始関数についての定理の証明\]
\( F(x) \) と \( G(x) \) はいずれも \( f(x) \) の原始関数なので、定義より、
\[ F'(x) = f(x) \]
\[ G'(x) = f(x) \]
が成り立つ。ここで、
\[ H(x) = F(x) - G(x) \]
とおくと、
\[ \begin{align}
H'(x) &= \left\{ F(x) - G(x) \right\} ' \\\\
&= F'(x) - G'(x) \\\\
&= f(x) - f(x) \\\\
&=0
\end{align} \]
よって、\( H(x) \) は \( C \) を任意の定数として \( H(x) = C \) となるから、
\[ H(x) = C = F(x) - G(x) \]
が成り立つ。ゆえに、
\[ F(x) = G(x) + C \]
が成り立つ。
この定理から、すべての原始関数はある原始関数 \( F(x) \) およびある定数 \( C \) を用いて \( F(x) + C \) と表せることになります。
そこで、これを不定積分の定義とします。
\[ 不定積分\]
\( F (x) \) を \( f (x) \) のある原始関数とする。このとき、\[ F (x) + C \ \ (C は任意の定数) \] を \( f (x) \) の不定積分といい \[ \int f (x) dx \] と表す。また、 \( C \) を特に積分定数という。関数 \( f(x) \) の不定積分を求めることを積分すると呼ぶ。
ナユミ
\( \int \) って、よくみるとおしゃれね \( \int \int \) 。
カヤ
流線形で綺麗だよな。で、話を戻すと不定積分の定義から、まずもって次のことがわかる。
\[ \left\{ \int f(x)dx \right\} ' = f(x) \]
\[ \int f'(x)dx = f(x) + C \]
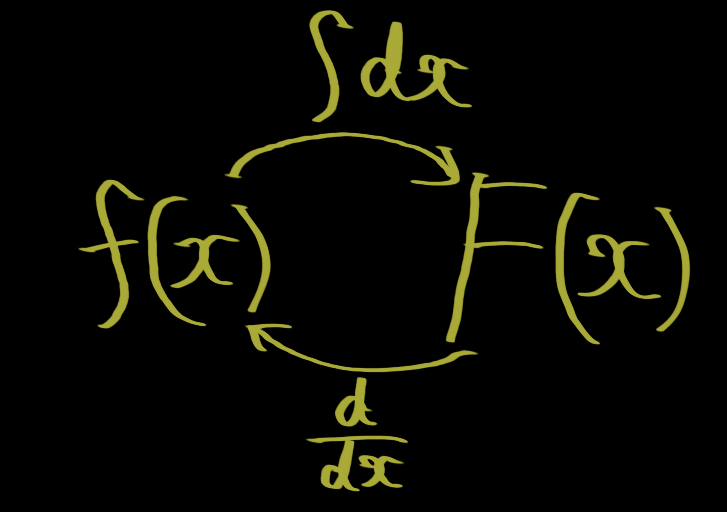
上の式は、積分した関数を微分すると元の関数に戻ることを、下の式は微分した関数を積分すると元の関数に任意の定数を足したものになることを意味しています。
これら2つの式が不定積分は微分の逆操作ということを表しています。
ナユミ
上下の式でループが作れるのね。
カヤ
そういうことだな。次に、定数倍と和、差の微分の公式を思い返せば、次の式が成り立つことがわかる。
\[ \int cf(x)dx = c \int f(x)dx + C \ \ \left( c \ \rm は定数 \it \right) \]
\[ \int \left\{ f(x) \pm g(x) \right\} dx = \int f(x)dx \pm \int g(x)dx + C \]
ナユミ
そうね、あの公式と似た形をしているわ。
カヤ
そうだろ。まずは定数倍の方の式を導出してみよう。
\[ \begin{align}
c \int f(x)dx &= c \left\{ F(x) + C_1 \right\} \\\\
&= cF(x) + cC_1 \\\\
\end{align} \]
\[ \begin{align}
\int \left\{ cF(x) + cC_1 \right\} ' dx &= \int cF'(x) dx \\\\
&= \int cf(x) dx \\\\
&= c \int f(x)dx + C
\end{align}\]
よって、
\[ \int cf(x) dx = c \int f(x)dx + C \]
カヤ
続いて、和と差の方を導出しよう。
\[ \int f(x)dx \pm \int g(x)dx = \left\{ F(x) + C_1 \right\} \pm \left\{ G(x) + C_2 \right\} \]
\[ \begin{align}
\int \left\{ \left\{ F(x) + C_1 \right\} \pm \left\{ G(x) + C_2 \right\} \right\} ' dx &= \int \left\{ \left\{ F(x) + C_1 \right\} ' \pm \left\{ G(x) + C_2 \right\} ' \right\} dx \\\\
&= \int \left\{ F'(x) \pm G'(x) \right\} dx \\\\
&= \int \left\{ f(x) \pm g(x) \right\} dx \\\\
&= \int f(x)dx \pm \int g(x)dx + C
\end{align}\]
よって、
\[ \int \left\{ f(x) \pm g(x) \right\} dx = \int f(x)dx \pm \int g(x)dx + C \]
ナユミ
他にも不定積分の一般的な公式はあるの？
カヤ
あと二つほど紹介しよう。一つ目は置換積分の公式だな。
\[ 置換積分 \]
\( x = g(u) \) が微分可能ならば次の式が成り立つ。
\[ \int f(x)dx = \int f(g(u))g'(u)du + C \]
\[ \int f(x)dx = \int f(g(u))g'(u)du + C \]
ナユミ
置換というのは、変数を \( x \) から \( u \) に置き換えたってことかしら？
カヤ
それで合ってるよ。置換積分の公式の導出は次の通りだ。
\( x = g(u) \) とおく。
\[ \int f(x)dx = F(x) + C \]
の両辺を \( u \) で微分すると、
\[ \begin{align}
\frac{d}{du} \left\{ \int f(x)dx \right\} &= \frac{d}{du} F(x) + 0 \\\\
&= \frac{d}{dx} F(x) \frac{dx}{du} \\\\
&= f(x) \frac{dx}{du} \\\\
&= f(g(u))g'(u) \\\\
\end{align} \]
よって、
\[ \frac{d}{du} \left\{ \int f(x)dx \right\} = f(g(u))g'(u)\]
不定積分の定義より、
\[ \int f(x)dx = \int f(g(u))g'(u)du + C \]
この公式を、
\[ x = g(u) \]
\[ g'(u) = \frac{dx}{du} \]
を用いて書き直すと、
\[ \int f(x)dx = \int f(x) \frac{dx}{du} du + C \]
となり、形式的には \( \frac{dx}{du} \) の分母を払ったような形になっています。
カヤ
それじゃあ、もう一つの一般的な公式である部分積分について紹介しよう。
\[ 部分積分 \]
\( f(x) \) 、\( g(x) \) がともに微分可能なら、次の式が成り立つ。
\[ \int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx + C \]
\[ \int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx + C \]
ナユミ
なんだか複雑そうね。
カヤ
見た目はややこしいが、導出は意外と簡単だ。積の微分公式を使う。
積の微分公式、
\[ \left\{ f(x)g(x) \right\} ' = f'(x)g(x) + f(x)g'(x) \]
において、右辺の \( f'(x)g(x) \) を移項し、両辺を逆にすると、
\[ f(x)g'(x) = \left\{ f(x)g(x) \right\} ' - f'(x)g(x) \]
両辺の不定積分を考えて、
\[ \begin{align}
\int f(x)g'(x)dx &= \int \left\{ f(x)g(x) \right\} ' dx - \int f'(x)g(x) dx \\\\
&= f(x)g(x) - \int f'(x)g(x) dx + C
\end{align} \]
ナユミ
見かけによらないものね。
カヤ
そうだろ。不定積分の一般的な公式はこれで終わりにして、最後に具体的な関数の不定積分を見ていこう。
様々な関数の不定積分
ナユミ
不定積分は微分の逆操作だから、関数の不定積分は微分したらその関数になる関数のことよね。
カヤ
その通りだな。前回具体的な関数の微分を色々見てきたので、それを思い出しながら見ていこう。
\[ \begin{align}
\ \ \ &\int x^{n} dx = \frac{1}{n+1} x^{n+1} + C \ \ ( n \ \rm{は} -1 \rm{を除く整数、} \it{x} \ \rm{は実数} ) \\\\
&\int \frac{1}{x} dx = \ln x + C \ \ ( x \rm \gt 0 ) \\\\
&\int x^{a} dx = \frac{1}{a+1} x^{a+1} + C \ \ ( a \ \rm{は} -1 \rm{を除く実数、} \it{x} \ \rm{は正の実数} )
\end{align}\]
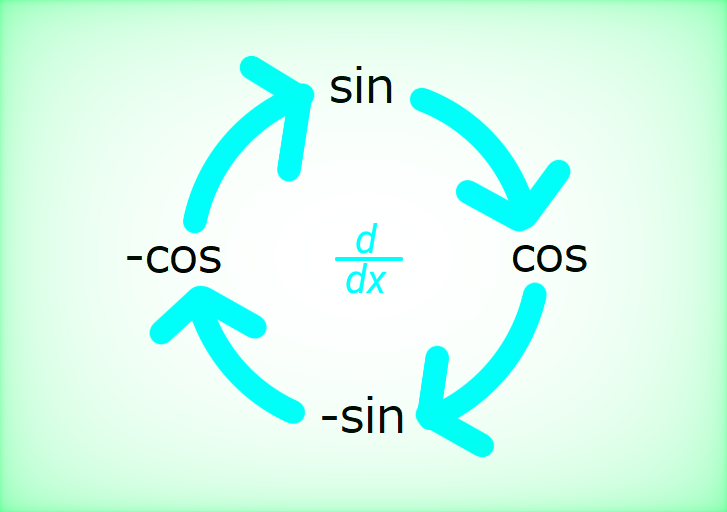
三角関数 \[ \begin{align} &\int \sin x dx = - \cos x + C \ \ (x \ \rm は実数)\\\\ &\int \cos x dx = \sin x + C \ \ (x \ \rm は実数)\\\\ &\int \frac{1}{\cos ^2 x} dx = \tan x + C \ \ (x \ \rm は \ \it n \ \rm を整数として、\frac{(2 \it n \rm -1) \pi}{2} \ を除く実数) \end{align}\]
指数関数 \[ \begin{align} &\int e^x dx = e^x + C \ \ ( x \ \rm{は実数} ) \\\\ &\int a^x dx = \frac{a^x}{\ln a} + C \ \ ( x \ \rm{は実数、} \ \it{a} \ \rm{は} \ 1 \ {を除く正の実数} ) \end{align}\]
三角関数 \[ \begin{align} &\int \sin x dx = - \cos x + C \ \ (x \ \rm は実数)\\\\ &\int \cos x dx = \sin x + C \ \ (x \ \rm は実数)\\\\ &\int \frac{1}{\cos ^2 x} dx = \tan x + C \ \ (x \ \rm は \ \it n \ \rm を整数として、\frac{(2 \it n \rm -1) \pi}{2} \ を除く実数) \end{align}\]
指数関数 \[ \begin{align} &\int e^x dx = e^x + C \ \ ( x \ \rm{は実数} ) \\\\ &\int a^x dx = \frac{a^x}{\ln a} + C \ \ ( x \ \rm{は実数、} \ \it{a} \ \rm{は} \ 1 \ {を除く正の実数} ) \end{align}\]
ナユミ
たくさんあるわね。
カヤ
まあな。だけど、前回やった微分公式を知っていれば理解できるはずだ。
ナユミ
この公式を全部証明するのはまた大変そうね…。
カヤ
そうでもないぞ。というのも、右辺を微分したものが左辺で積分されている関数になっていることを確認できれば十分だからな。全部はやらないが、例として一番上の \( x^n \) の積分について確かめてみよう。
\[ \left\{ \frac{1}{n+1} x^{n+1} + C \right\} ' = \frac{1}{n+1} (n+1)x^{(n+1)-1} = x^n \]
ナユミ
ふむふむ、そうやって確かめていけばいいのね。これならそこまで大変でもなさそう。
カヤ
そうだろ。また時間のあるときにでもやっておいてくれな。
ナユミ
わかったわ。
参考：
[1] George Allen & Unwin Ltd 著、矢野健太郎 訳補、ブルーバックス 現代数学百科、講談社、1968年11月30日発行
[2] 石村園子、やさしく学べる微分積分、共立出版、1999年12月25日発行
前の記事
第7話
様々な関数の微分
様々な関数の微分
次の記事
第9話
オイラー法
オイラー法