オイラー法

　　・オイラー法

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 5話、 6話、 7話、 8話

カヤ

今回は常微分方程式の基本的な数値積分であるオイラー法について解説していこう。

オイラー法

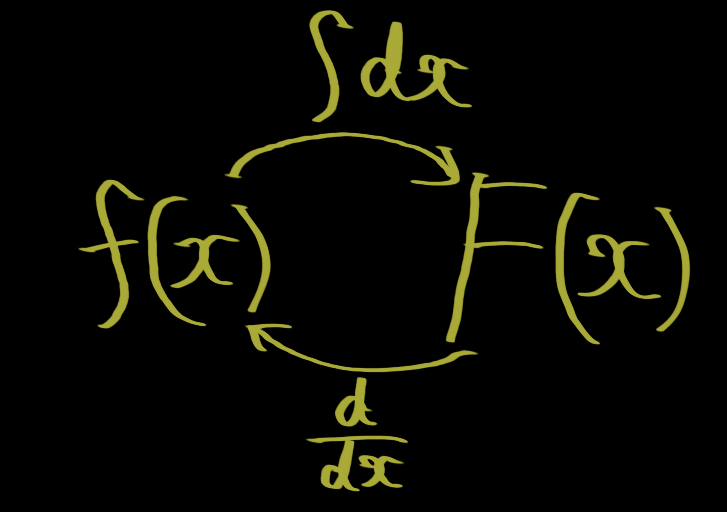
　未知関数の変数の数が1個の微分方程式のことを常微分方程式と呼びます。微分方程式の数値積分とは、微分方程式を不定積分を使って解くのではなく、適切な近似法を用いて数値解と呼ばれる解の近似値を求める方法です。微分方程式の中には不定積分を求める方法がわかっていないものや、特殊な関数を用いなければ不定積分を表すことができないものがあります。そのような場合に、数値積分は有用です。

ナユミ

今までの微分方程式は序の口だったのね…。

カヤ

まあな。世の中にはいろいろな微分方程式があるのさ。

ナユミ

そうだったのね。それでオイラー法はどういう方法なのかしら？

カヤ

オイラー法は微分係数の定義の見方を少し変えたものだ。

\[ オイラー法\] 　常微分方程式の数値積分の一つ。未知関数 \( y = f(x) \) についてその導関数 \( y' = f'(x) \) が既知であるとする。このとき、刻み幅を \( h \) 、初期値を \( \left( x_0,y_0 \right) \) として、数値解 \( \left( x_n,y_n \right) \) \( ( n \ \rm は自然数 )\) を次のように求める。 \[ \begin{align} x_n &= x_{n-1} + h \\\\ y_n &= y_{n-1} + hf'(x_{n-1}) \end{align}\]

ナユミ

これのどこが微分係数なの？

カヤ

\( y_n \) を少し変形してみるとわかる。

\[ \begin{align} y_n &= y_{n-1} + hf'(x_{n-1}) \\\\ y_n - y_{n-1} &= hf'(x_{n-1}) \\\\ \frac{y_n - y_{n-1}}{h} &= f'(x_{n-1}) \\\\ f'(x_{n-1}) &= \frac{y_n - y_{n-1}}{h} \end{align}\]

カヤ

これと \( x_{n-1} \) における微分係数の定義を並べてみよう。

オイラー法 \[ f'(x_{n-1}) = \frac{y_n - y_{n-1}}{h} \] \( x_{n-1} \) における微分係数 \[ \begin{align} f'(x_{n-1}) &= \lim_{h \to 0} \frac{f(x_{n-1}+h) - f(x_{n-1})}{h} \\\\ &= \lim_{h \to 0} \frac{f(x_{n}) - f(x_{n-1})}{h} \end{align} \]

　\( y_n = f(x_n) \) とみなすと、オイラー法と \( x_{n-1} \) における微分係数は極限の記号の有無以外は同じです。オイラー法は微分係数の定義で \( h \to 0 \) の極限として扱っていたところを、あえてある一定の幅を持つ \( h \) として扱うことで \( y_n \) の値を初期値から求めることを可能にしています。

ナユミ

これって実際にやってみるとどんな感じなの？

カヤ

そうだな。\( y = \frac{1}{4} x^2 \) をオイラー法を使って計算した例を見てみよう。\( \left( x_0,y_0 \right) = (0,0) \) として、わかりやすいように、刻み幅は \( h = \frac{1}{2} \) と大きめに取ってある。

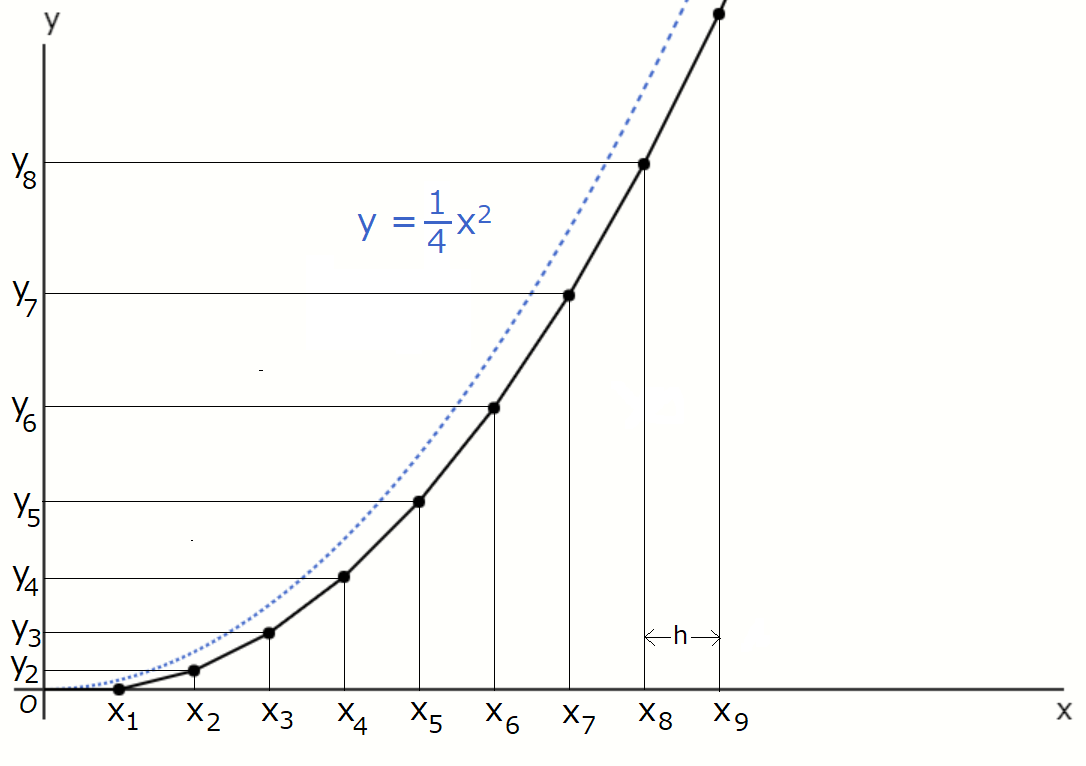
　黒線がオイラー法で求めた数値解、青の破線が \( y = \frac{1}{4} x^2 \) の真の解です。実際にオイラー法で求めているのは黒丸の部分で、黒丸間の黒線はわかりやすいように黒丸同士を結んであるだけなので注意してください。

ナユミ

この例だと、ちゃんとした値からオイラー法の結果は少しずれてるけど、刻み幅をもっと小さくすれば、もっとちゃんと求まるのよね？

カヤ

ああ。刻み幅を \( h = \frac{1}{10} \) としたらこうなるな。

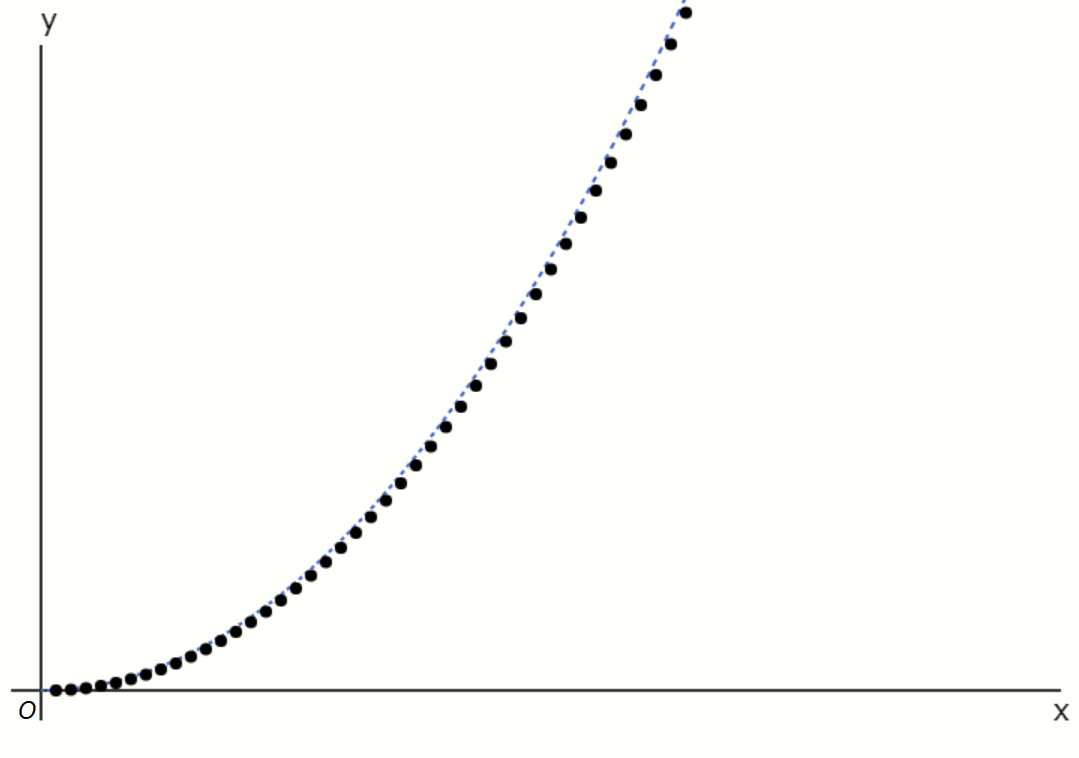
　オイラー法で求めた数値解 \( y_n \) とちゃんとした値との誤差はおおよそ刻み幅 \( h \) に比例することが知られています。ただし、刻み幅を小さくすればするほど計算回数が増え、コンピュータで数を計算するときに数を四捨五入することによって生じる誤差（丸め誤差）の影響が大きくなるため、刻み幅はとにかく小さくすればいいというものではありません。また、計算にかかる時間をなるべく短くするという観点からも、刻み幅を小さくしすぎて計算回数が増えすぎるのはよくないため、適切な刻み幅を設定する必要があります。

ナユミ

実際の計算はいろいろと難しいわね。

カヤ

まあな。いろいろと気を付けるべき細かいポイントはあるが、数値積分が微分方程式の解を調べる有効な手段であることには違いない。今後は数値実験でも数値積分を用いて解を求めることがあるだろうからよろしくな。

ナユミ

了解よ。

　最後に、オイラー法を発案したレオンハルト・オイラーはスイス生まれの18世紀の数学者です。彼は数学や物理学の様々な分野の基礎を築き上げた人物で、彼の名を冠した定理や方程式がたくさんあり、オイラー法もそのうちの一つです。

レオンハルト・オイラー(1707-1783)

参考：
[1] Euler method、https://en.wikipedia.org/wiki/Euler_method、2023年8月14日閲覧
[2] オイラー法の誤差について、https://hinabit.hatenablog.com/entry/2015/02/13/015201、2023年8月14日閲覧
[3] スタンリー・ファーロウ著、伊理正夫・伊理由美訳、偏微分方程式―科学者・技術者のための使い方と解き方、朝倉書店、1996年12月1日発行
[4] Wikipedia レオンハルト・オイラー、https://ja.wikipedia.org/wiki/レオンハルト・オイラー、2024年5月23日閲覧

第8話
不定積分

第10話
一変数関数の増減と極値