一変数関数の増減と極値

　　・関数の増減と極値

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 6話

カヤ

今回は一変数関数の増減と極値について解説していこう。

関数の増減と極値

ナユミ

関数は増えたり減ったりするわね。

カヤ

そうだろう。その増えたり減ったりについて、微分係数を用いて次のように特徴づけられるんだ。

　一変数関数 $ y = f(x) $ が $ a $ を含む実区間で微分可能とする。このとき、 \[ f'(a) \gt 0 \rm \ ならば、\it f \rm ( \it x \rm ) \ は \ \it x \rm = \it a \rm \ で増加傾向 \] \[ f'(a) \lt 0 \rm \ ならば、\it f \rm ( \it x \rm ) \ は \ \it x \rm = \it a \rm \ で減少傾向 \] である。

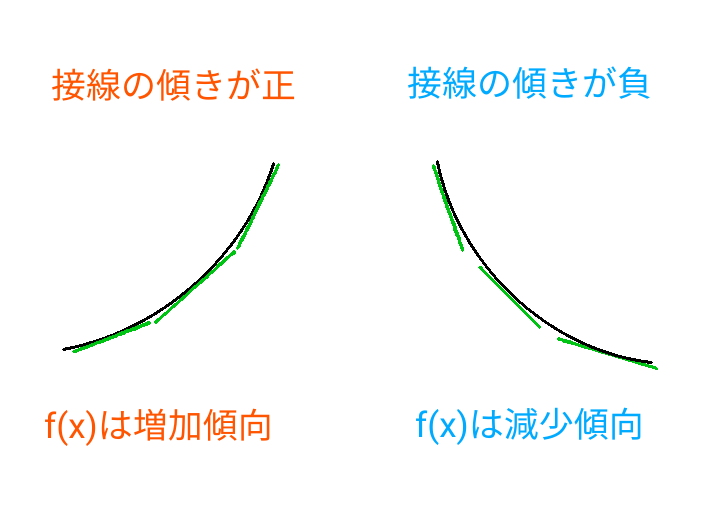
　一変数関数の微分係数は接線の傾きです。つまり上の記述は、接線の傾きがプラスなら関数は増加傾向、逆に接線の傾きがマイナスなら関数は減少傾向ということを言っています。図で表すと次のようになります。

ナユミ

接線が右上がりなら関数は増加していて、逆に右下がりなら関数は減少しているのね。図で見ると当たり前ね。

カヤ

そうだな。じゃあ、続けて極値の解説をしよう。

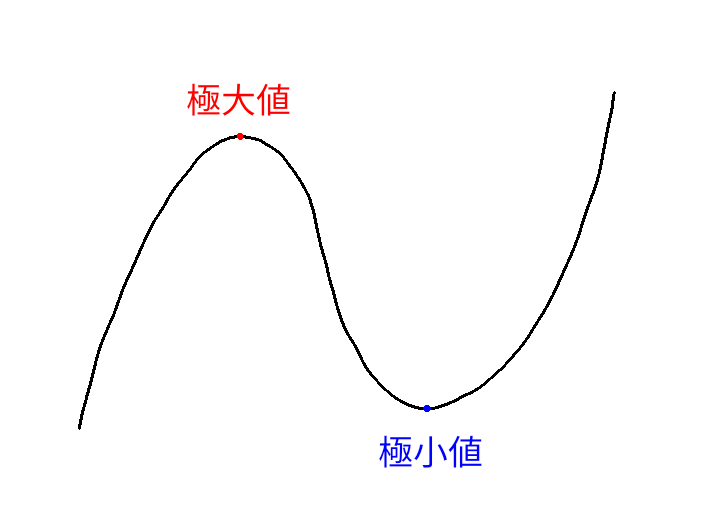
　一変数関数 $ y = f(x) $ が $ x = a $ を境にして増加傾向から減少傾向に転ずるとき、$ y = f(x) $ は $ x = a $ において極大になるといい、$ f(a) $ を極大値と呼ぶ。
　逆に、一変数関数 $ y = f(x) $ が $ x = a $ を境にして減少傾向から増加傾向に転ずるとき、$ y = f(x) $ は $ x = a $ において極小になるといい、$ f(a) $ を極小値と呼ぶ。
　極大値と極小値を合わせて極値と呼ぶ。

ナユミ

山、というより尾根筋と谷の底ってことね。

カヤ

そういうことだな。極大値は最大値とは異なるから、山ではなく尾根筋というのはいい喩えかもな。

ナユミ

この山はまだ谷の右側に向けて登っていけそうだからね。

カヤ

そうだな。それと、極値について次が成り立っている。

　一変数関数 $ y = f(x) $ が $ a $ を含む実区間で微分可能とする。このとき、$ y = f(x) $ が $ x = a $ で極値を取れば $ f'(a) = 0 $ である。

　極値では増加と減少が切り替わる、つまり、微分係数の値が正から負へと切り替わるので、その切り替わりポイントでは $ f'(a) = 0 $ になるということです。この性質を使うと、関数のグラフが尾根筋や谷底を持っているときに、そのときの $ x $ の値を調べたり、あるいは関数全体に尾根筋や谷底があるかどうかなどを調べることができます。

ナユミ

いろいろと便利そうね。

カヤ

ああ。今後使うこともあるだろうから覚えておいてくれ。

ナユミ

わかったわ。

参考：
[1] 石村園子、やさしく学べる微分積分、共立出版、1999年12月25日発行

第9話
オイラー法

$partial_fraction$

第11話
部分分数分解