目次
・部分分数分解
カヤ
今回は部分分数分解について解説していこう。
部分分数分解
部分分数分解は分数を2つに分ける操作のことです。
まずは基本の形として、次の分解を考えてみます。
\[ \frac{1}{ab} = k \left( \frac{1}{a} + \frac{1}{b} \right) \]
この式を満たす \( k \) は？
ナユミ
ふーむ、これは右辺のかっこの中を通分したらわかるんじゃないかしら。
\[ \begin{align}
\frac{1}{ab} &= k \left( \frac{1}{a} + \frac{1}{b} \right) \\\\
\frac{1}{ab} &= k \left( \frac{a+b}{ab} \right)
\end{align}\]
両辺を比較すると、
\[ 1 = k \left( a+b \right) \]
よって、
\[ k = \frac{1}{a+b} \]
カヤ
正解だ。この結果から、次式が成り立つとわかる。
\[ \frac{1}{ab} = \frac{1}{a+b} \left( \frac{1}{a} + \frac{1}{b} \right) = \frac{1}{a \left( a + b \right) } + \frac{1}{b \left( a + b \right)} \]
ナユミ
一番右の式はかっこの中をまた展開したのね。
カヤ
そうだ。この一番右の式にあるそれぞれの分数はこの公式を再び適用してさらに分解することもできる。
\[ \begin{align}
\frac{1}{a \left( a + b \right) } &= \frac{1}{a + \left( a + b \right)} \left( \frac{1}{a} + \frac{1}{a+b} \right) \\\\
&= \frac{1}{2a+b} \left( \frac{1}{a} + \frac{1}{a+b} \right) \\\\
\frac{1}{b \left( a + b \right)} &= \frac{1}{b + \left( a + b \right)} \left( \frac{1}{b} + \frac{1}{a+b} \right) \\\\
&= \frac{1}{a + 2b} \left( \frac{1}{b} + \frac{1}{a+b} \right)
\end{align}\]
ナユミ
ほうほう。上の式は \( a = a \) 、\( b = a + b \) として公式を使っていて、下の式は \( a = b \) 、\( b = a + b \) として公式を使っているのね。公式に同じ公式を使うって、マトリョーシカ的ね。
カヤ
そんな感じだな。この分解を繰り返していける性質を使うと、例えばこんなこともできる。
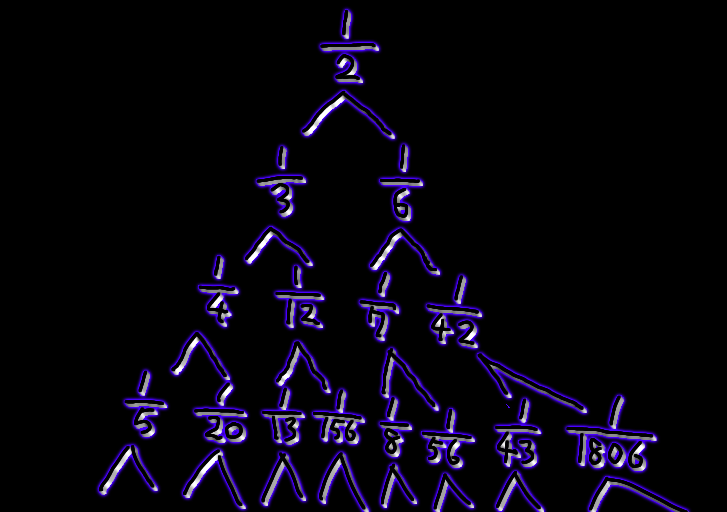
\[ \begin{align}
\frac{1}{2} &= \frac{1}{1 \cdot 3} + \frac{1}{2 \cdot 3} \\\\
&= \frac{1}{1 \cdot 4} + \frac{1}{3 \cdot 4} + \frac{1}{2 \cdot 5} + \frac{1}{3 \cdot 5} \\\\
&= \frac{1}{1 \cdot 5} + \frac{1}{4 \cdot 5} + \frac{1}{3 \cdot 7} + \frac{1}{4 \cdot 7} + \frac{1}{2 \cdot 7} + \frac{1}{5 \cdot 7} + \frac{1}{3 \cdot 8} + \frac{1}{5 \cdot 8} \\\\
&= \ldots
\end{align}\]
ナユミ
どこまでも分解していけるのね。頭クラクラしてきたわ…。
カヤ
まあ、これはちょっと遊んだだけだから、そんな気にしなくてもいいぞ。
ナユミ
聞き流しておくわね。
カヤ
そうしておいてくれ。じゃあ、次にこの問題を考えてみよう。
\[ \frac{1}{\left( ax+b \right) \left( cx+d \right)} = \left( \frac{p}{ax+b} + \frac{q}{cx+d} \right) \]
この式を満たす \( p \) 、\( q \) は？
ナユミ
この形は何回か見たことあるような気がするわ…。
カヤ
そうだろうな。左辺の形の式が出てきたときに、右辺の形に直してから不定積分をすることが何回かあったな。
ナユミ
これも右辺を通分すればよさそうね。
\[ \begin{align}
\frac{1}{\left( ax+b \right) \left( cx+d \right)} &= \left( \frac{p}{ax+b} + \frac{q}{cx+d} \right) \\\\
&= \frac{p \left( cx+d \right) + q \left( ax+b \right)}{\left( ax+b \right) \left( cx+d \right)} \\\\
&= \frac{\left( cp + aq \right) x + dp + bq}{\left( ax+b \right) \left( cx+d \right)}
\end{align}\]
ナユミ
ここからどうするんだっけ？
先ほどと同じように左辺と右辺を比較します。
ただし、今求めたいのは \( p \) と \( q \) なので、これらについての式を2本立てる必要があります。
一方で、\( x \) は分母にも出ている文字で、これが \( a \) や \( b \) といった分母にある他の記号で表されると分母を書き換えられることになってしまい、これは都合がよくありません。
そこで、分子にある \( x \) にかけられている部分を0とし、\( x \) が無関係の部分を1と置いて対処します。
\[ \begin{align}
[1] \ \ \ \ cp + aq &= 0 \\\\
[2] \ \ \ \ dp + bq &= 1
\end{align}\]
ナユミ
ほうほう、こうすれば都合よく \( p \) 、\( q \) についての式を2本作れるのね。
カヤ
そういうことだな。これは次のように解ける。
[1]より、
\[ q = - \frac{c}{a} p \]
これを[2]に代入して、
\[ \begin{align}
dp - \frac{bc}{a} p &= 1 \\\\
p \left( d - \frac{bc}{a} \right) &= 1 \\\\
p \cdot \frac{ad - bc}{a} &= 1 \\\\
p &= \frac{a}{ad - bc}
\end{align}\]
よって、
\[ \begin{align}
q &= - \frac{c}{a} p \\\\
&= - \frac{c}{a} \cdot \frac{a}{ad - bc} \\\\
&= - \frac{c}{ad - bc}
\end{align}\]
ナユミ
[1]を変形して \( q \) を \( p \) で表した後に、それを[2]に代入して \( p \) を求めて、それをまた[1]に戻して \( q \) を求めているのね。
カヤ
そういう流れだな。これらを最初に問題にした式に戻すとこうなる。
\[ \begin{align}
\frac{1}{\left( ax+b \right) \left( cx+d \right)} &= \left( \frac{p}{ax+b} + \frac{q}{cx+d} \right) \\\\
&= \left( \frac{\frac{a}{ad - bc}}{ax+b} + \frac{- \frac{c}{ad - bc}}{cx+d} \right) \\\\
&= \frac{1}{ad - bc} \left( \frac{a}{ax+b} - \frac{c}{cx+d} \right)
\end{align}\]
ナユミ
この式が、カヤちゃんがよく数値実験で積分するときに使っている公式なのね。
カヤ
そういうことだ。今後も時々出てくるかもしれないから、覚えておいてくれよな。
ナユミ
わかったわ。
参考：
[1] Partial fraction decomposition、https://en.wikipedia.org/wiki/Partial_fraction_decomposition、2023年8月26日閲覧
前の記事
第10話
一変数関数の増減と極値
一変数関数の増減と極値
次の記事
第12話
二分法・ニュートン法
二分法・ニュートン法