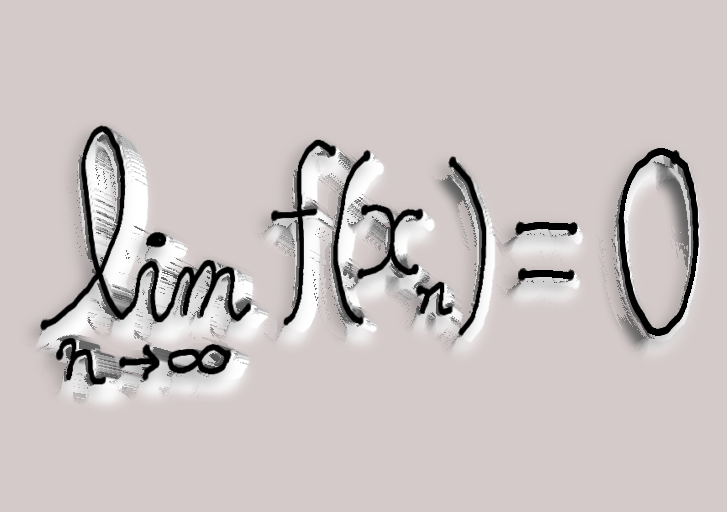
目次
・二分法
・ニュートン法
カヤ
今回は方程式 \( f(x) = 0 \) の数値解を求める方法を二つ紹介しよう。一つ目は二分法だ。
二分法
ナユミ
二分法って前にやったことあったよね。
カヤ
そうだな。あの時は \( \sqrt{2} \) を求めるために二分法を使った。あれをもっと一般的に方程式 \( f(x) = 0 \) の解を求めるための方法として説明すると次のようになる。
\[ 二分法 \]
一変数関数 \( f(x) \) について、\( f(x) = 0 \) となる \( x \) を近似的に求める方法の一つ。次の手順からなる。
[1] \( f(a_0)f(b_0) \lt 0 , f(a_0) \gt 0 \) を満たす適当な初期値 \( a_0 , b_0 \) を与える。
[2] \( f \left( \frac{a_0 + b_0}{2} \right) \gt 0 \) ならば \( a_1 = \frac{a_0 + b_0}{2} , \ b_1 = b_0 \) とし、\( f \left( \frac{a_0 + b_0}{2} \right) \lt 0 \) ならば \( a_1 = a_0 , \ b_1 = \frac{a_0 + b_0}{2} \) とする。
[3] 以後同様に、\( a_k , b_k \ \ (k = 1, 2, 3, \ldots ) \) を用いて \( a_{k+1} , b_{k+1} \) を求める操作を繰り返す。すると、 \[ \lim _{k \to \infty} f \left( \frac{a_k + b_k }{2} \right) = 0 \]となる。
[1] \( f(a_0)f(b_0) \lt 0 , f(a_0) \gt 0 \) を満たす適当な初期値 \( a_0 , b_0 \) を与える。
[2] \( f \left( \frac{a_0 + b_0}{2} \right) \gt 0 \) ならば \( a_1 = \frac{a_0 + b_0}{2} , \ b_1 = b_0 \) とし、\( f \left( \frac{a_0 + b_0}{2} \right) \lt 0 \) ならば \( a_1 = a_0 , \ b_1 = \frac{a_0 + b_0}{2} \) とする。
[3] 以後同様に、\( a_k , b_k \ \ (k = 1, 2, 3, \ldots ) \) を用いて \( a_{k+1} , b_{k+1} \) を求める操作を繰り返す。すると、 \[ \lim _{k \to \infty} f \left( \frac{a_k + b_k }{2} \right) = 0 \]となる。
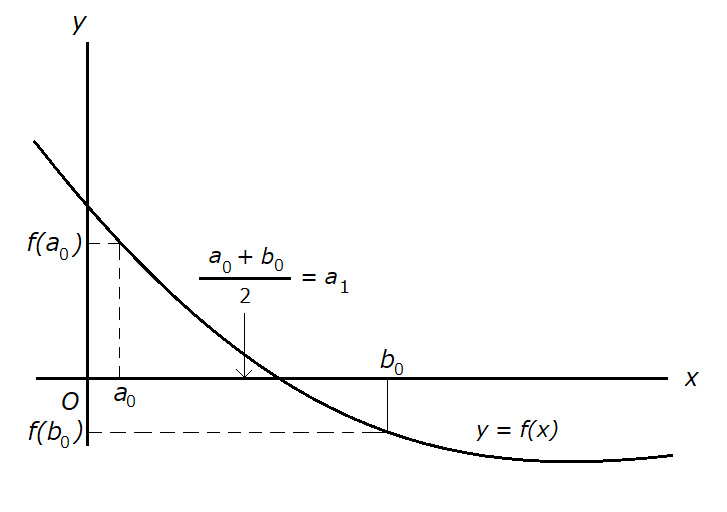
二分法は \( a_k \) と \( b_k \) で \( f(x) = 0 \) の解を挟みながら、解に近づいていきます。
\( k \geq 1 \) について、
\[ 0 \leq f \left( a_k \right) \leq f \left( a_{k-1} \right) \]
\[ 0 \geq f \left( b_k \right) \geq f \left( b_{k-1} \right) \]
が成り立つため、\( a_k \) も \( b_k \) も \( k \) を大きくすれば確実に解に近づいていくという特徴があります。
ナユミ
癖のない、真っすぐな方法ね。
カヤ
そうだな。\( f(x) \) の形によらず数列が必ず解に収束するのが二分法のいいところだな。それじゃあ次はニュートン法を紹介しよう。
ニュートン法
ナユミ
ニュートンって聞いたことがある名前ね。
カヤ
ニュートンは17世紀に活躍した科学者だ。微積分学の発展に貢献した人物の一人でもある。
アイザック・ニュートン(1642年-1727年)
ナユミ
微分や積分を作った人の一人なのね。それで、ニュートン法ってどういう方法なのかしら？
カヤ
こういう方法だな。
\[ ニュートン法 \]
実数全体において微分可能な一変数関数 \( f(x) \) について、\( f(x) = 0 \) となる \( x \) を近似的に求める方法の一つ。次の手順からなる。
[1] \( f(x_0) \neq 0 \) を満たす適当な初期値 \( x_0 \) を与える。
[2] 次式を用いて、\( x_k \ \ \left( k = 1,2,3, \ldots \right) \) を順次求めていく。 \[ x_{k} = x_{k-1} - \frac{f \left( x_{k-1} \right) }{f' \left( x_{k-1} \right) } \]
[3] 初期値の選び方によっては、 \[ \lim _{k \to \infty} f \left( x_k \right) = 0 \] となる。ただし、初期値の選び方によっては、この式が成り立たないこともある。
[1] \( f(x_0) \neq 0 \) を満たす適当な初期値 \( x_0 \) を与える。
[2] 次式を用いて、\( x_k \ \ \left( k = 1,2,3, \ldots \right) \) を順次求めていく。 \[ x_{k} = x_{k-1} - \frac{f \left( x_{k-1} \right) }{f' \left( x_{k-1} \right) } \]
[3] 初期値の選び方によっては、 \[ \lim _{k \to \infty} f \left( x_k \right) = 0 \] となる。ただし、初期値の選び方によっては、この式が成り立たないこともある。
カヤ
こうなるな。
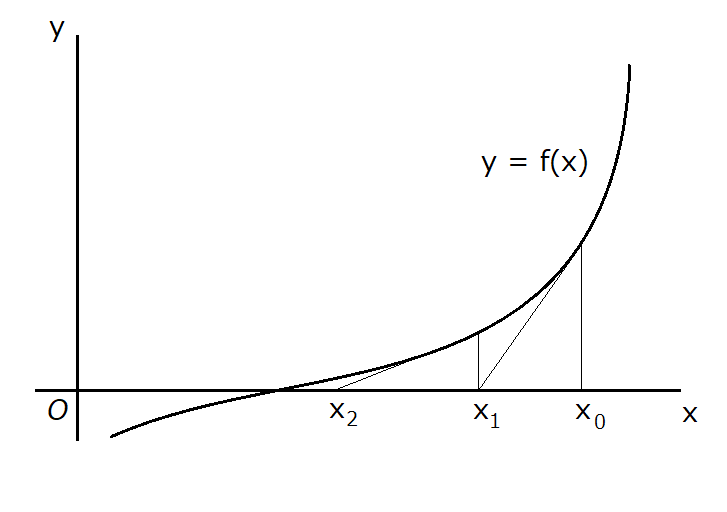
二分法とは異なり、ニュートン法は \( f(x) \) が微分可能な関数であり、その導関数 \( f'(x) \) がわかっているときしか使えません。
反復計算は \( x_0 \) から始まり、点 \( \left( x_0 , f \left( x_0 \right) \right) \) における接線と \( x \) 軸が交わる点を \( x_1 \) とする、というループを繰り返していきます。
また、ニュートン法は二分法とは異なり、数列が収束しない場合があります。
例えば、
\[ f(x) = x^3 -2x + 2\]
について、初期値を \( x_0 = 0 \) としてニュートン法を実行すると、次のように \( x_2 = x_0 \) となり無限ループに入ってしまいます。
\[ f' (x) = 3 x^2 -2 \]
であるから、
\[ \begin{align}
x_{1} &= x_0 - \frac{f \left( x_0 \right) }{ f' \left( x_0 \right) } \\\\
&= 0 - \frac{0^3 -2 \cdot 0 + 2}{3 \cdot 0^2 -2} \\\\
&= 0 - (-1) = 1 \\\\
x_{2} &= x_1 - \frac{f \left( x_1 \right) }{ f' \left( x_1 \right) } \\\\
&= 1 - \frac{1^3 -2 \cdot 1 + 2}{3 \cdot 1^2 - 2} \\\\
&= 1 - \frac{1}{1} = 0
\end{align}\]
ニュートン法には色々と問題点もありますが、条件さえ整えば数列の収束が二分法に比べると速いというメリットがあります。
実際に \( f(x) = 0 \) となる \( x \) の近似解を求める場合、先にニュートン法を試してみて、上手くいかないなら二分法を使うという手順を踏むのが定石です。
ナユミ
まずはニュートン法で、無理そうだったら安定の二分法に切り替えるのね。
カヤ
その流れがいいだろうな。
参考：
[1] Wikipedia アイザック・ニュートン、https://ja.wikipedia.org/wiki/アイザック・ニュートン、2023年9月4日閲覧
[2] Wikipedia Newton's method、https://en.wikipedia.org/wiki/Newton%27s_method 、2023年9月4日閲覧
[3] Wikipedia 二分法、https://ja.wikipedia.org/wiki/二分法、2023年9月4日閲覧
前の記事
第11話
部分分数分解
部分分数分解
次の記事
第13話
定積分
定積分