目次
・ルンゲ=クッタ法
・2次導関数への応用
カヤ
今回はルンゲ=クッタ法を解説しよう。
ルンゲ=クッタ法
ナユミ
ルンゲ=クッタ法ってたしか数値解法の名前よね？
カヤ
ああ。ルンゲ=クッタ法は常微分方程式の数値積分の一つで、オイラー法よりも高い精度を持つ手法だ。
\[ ルンゲ=クッタ法\]
常微分方程式の数値積分の一つ。未知関数 \( y = f(x) \) についてその導関数 \( y' = g \left( x , y \right) \) が既知であるとする。
このとき、刻み幅を \( h \) 、初期値を \( \left( x_0,y_0 \right) \) として、数値解 \( \left( x_n,y_n \right) \) \( ( n \ \rm
は自然数 )\) を次のように求める。
\[ \begin{align}
x_n &= x_{n-1} + h \\\\
y_n &= y_{n-1} + \frac{1}{6} h \left( k_1 + 2 k_2 + 2 k_3 + k_4 \right) \\\\
\end{align}\]
ここで、
\[ \begin{align}
k_1 &= g \left( x_{n-1} , y_{n-1} \right) \\\\
k_2 &= g \left( x_{n-1} + \frac{1}{2} h , y_{n-1} + \frac{1}{2} h k_1 \right) \\\\
k_3 &= g \left( x_{n-1} + \frac{1}{2} h , y_{n-1} + \frac{1}{2} h k_2 \right) \\\\
k_4 &= g \left( x_{n-1} + h , y_{n-1} + h k_3 \right) \\\\
\end{align}\]
上に書いたものは4次の古典的 Runge-Kutta 公式と呼ばれるもので、19世紀の終わり頃にはすでに知られていました。
ルンゲ=クッタ法には上の公式を元にした派生公式がいくつもあり、現在でも関連した様々な研究が続いています。
カヤ
一般論だけだとわかりにくいから、一つ具体例を見てみよう。
\[ \begin{align}
\frac{dy}{dx} = y
\end{align}\]
を4次の古典的 Runge-Kutta 公式により数値的に解く。
刻み幅を \( h \) とすれば、
\[ \begin{align}
k_1 &= y_{n-1} \\\\
k_2 &= y_{n-1} + \frac{1}{2} h y_{n-1} \\\\
k_3 &= y_{n-1} + \frac{1}{2} h \left( y_{n-1} + \frac{1}{2} h y_{n-1} \right) \\\\
&= y_{n-1} + \frac{1}{2} h y_{n-1} + \frac{1}{4} h^2 y_{n-1} \\\\
k_4 &= y_{n-1} + h \left( y_{n-1} + \frac{1}{2} h y_{n-1} + \frac{1}{4} h^2 y_{n-1} \right) \\\\
&= y_{n-1} + h y_{n-1} + \frac{1}{2} h^2 y_{n-1} + \frac{1}{4} h^3 y_{n-1}
\end{align}\]
よって、
\[ \begin{align}
& \ \ \ \ \ \ \frac{1}{6} h \left( k_1 + 2 k_2 + 2 k_3 + k_4 \right) \\\\
&= \frac{1}{6} h \left( 6 y_{n-1} + 3h y_{n-1} + h^2 y_{n-1} + \frac{1}{4} h^3 y_{n-1} \right) \\\\
&= h y_{n-1} + \frac{1}{2} h^2 y_{n-1} + \frac{1}{6} h^3 y_{n-1} + \frac{1}{24} h^4 y_{n-1}
\end{align}\]
従って、
\[ \begin{align}
x_n &= x_{n-1} + h \\\\
y_n &= y_{n-1} + h y_{n-1} + \frac{1}{2} h^2 y_{n-1} + \frac{1}{6} h^3 y_{n-1} + \frac{1}{24} h^4
y_{n-1}
\end{align}\]
これに初期値 \( \left( x_0,y_0 \right) \) を与え順に計算していくことで、数値解 \( \left( x_n,y_n \right) \) \( ( n \ \rm は自然数
)\) を得る。
微分方程式
\[ \begin{align}
\frac{dy}{dx} = y
\end{align}\]
の解は、初期値を \( \left( x_0 , y_0 \right) = \left( 0, 1 \right) \) とすれば、
\[ y = e^x \]
になります。この真の解とルンゲ=クッタ法で刻み幅 \( h = 0.1 \) として得られた数値解を比較すると、次図の通りです。
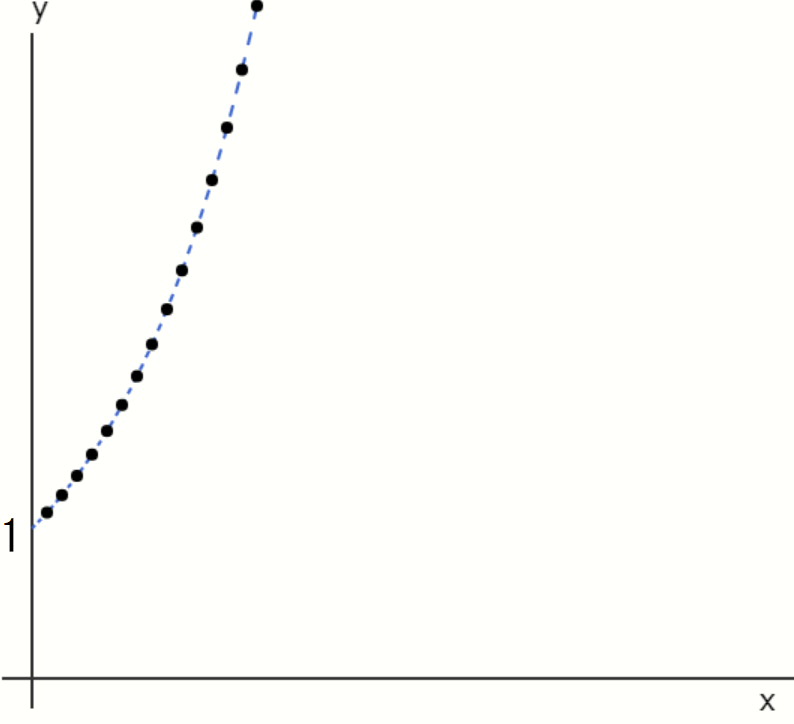
黒丸が数値解、青の破線が真の解。
ナユミ
よく一致しているわね。
カヤ
そうだな。次に、ルンゲ=クッタ法を2次導関数を含む微分方程式へと拡張しよう。
2次導関数への応用
4次の古典的 Runge-Kutta 公式は2次導関数が既知である場合に拡張できます。
未知関数 \( z = f(x) \) の2次導関数が
\[ \frac{d^2 z}{dx^2} = g(x,y,z) \]
と与えられている場合、
\[ y = \frac{dz}{dx} \]
とおくと、
\[ \frac{dy}{dx} = g(x,y,z) \]
となる。このとき、刻み幅を \( h \) 、初期値を \( \left( x_0,y_0,z_0 \right) \) として、数値解 \( \left( x_n,y_n ,z_n \right) \)
\( ( n \ \rm
は自然数 )\) を次のように求めることができる。
\[ \begin{align}
x_n &= x_{n-1} + h \\\\
y_n &= y_{n-1} + \frac{1}{6} h \left( k_1 + 2 k_2 + 2 k_3 + k_4 \right) \\\\
z_n &= z_{n-1} + \frac{1}{6} h \left( l_1 + 2 l_2 + 2 l_3 + l_4 \right) \\\\
\end{align}\]
ここで、
\[ \begin{align}
k_1 &= g \left( x_{n-1} , y_{n-1} , z_{n-1} \right) \\\\
l_1 &= y_{n-1} \\\\
k_2 &= g \left( x_{n-1} + \frac{1}{2} h , y_{n-1} + \frac{1}{2} h k_1 , z_{n-1} + \frac{1}{2} h l_1
\right) \\\\
l_2 &= y_{n-1} + \frac{1}{2} h k_1 \\\\
k_3 &= g \left( x_{n-1} + \frac{1}{2} h , y_{n-1} + \frac{1}{2} h k_2 , z_{n-1} + \frac{1}{2} h l_2
\right) \\\\
l_3 &= y_{n-1} + \frac{1}{2} h k_2 \\\\
k_4 &= g \left( x_{n-1} + h , y_{n-1} + h k_3 , z_{n-1} + h l_3 \right) \\\\
l_4 &= y_{n-1} + h k_3 \\\\
\end{align}\]
ナユミ
kとlを交互に求めてゆくのね。
カヤ
そうだな。数値実験の記事を読むのにルンゲ=クッタ法の具体的な計算法の理解が必要ということはないと思うが、このような式を使っているということは頭の片隅にでも置いておいてくれ。
ナユミ
わかったわ。
参考：
[1] 三井斌友、Runge-Kutta 法-その過去, 現在, 未来-、日本数学会、総合講演・企画特別講演アブストラクト、1998年、1998巻、Spring-Meeting号、p.93-101
前の記事
第20話
大数の弱法則
大数の弱法則
次の記事
第22話
偏微分
偏微分