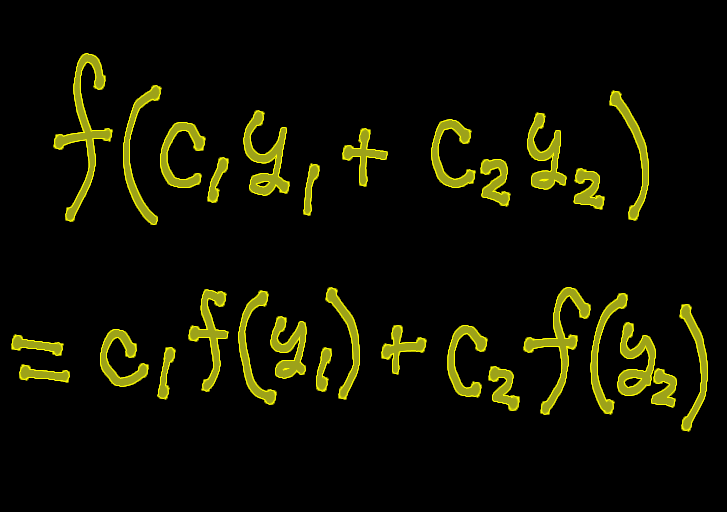
目次
・微分方程式の分類
・重ね合わせの原理
微分方程式の分類
微分方程式は未知関数の(偏)導関数を含む方程式のことです。未知関数が一変数関数の場合の微分方程式を常微分方程式と呼び、2変数以上の未知関数の場合を偏微分方程式と呼びます。微分方程式をみたす関数を微分方程式の解といいます。任意関数を含む解を一般解と呼び、任意関数を特別に定めたものを特解と呼びます。
微分方程式に含まれる(偏)導関数の最高次数が \( n \) 次(偏)導関数であるとき、それを \( n \) 階の微分方程式といいます。
未知関数およびその(偏)導関数を独立変数 \( \mathfrak D \) とする一次関数の形からなる項 \[ a \mathfrak D \rm + \it b \] を考えます。ここで \( a \) および \( b \) は任意の既知関数とします。 このような項のみを含む微分方程式を線形といい、線形でないものを非線形といいます。
すべての項が未知関数およびその(偏)導関数を含むか 0 である微分方程式を同次といい、そうでないものを非同次といいます。
一般論だけだとわかりにくいので具体例を見てみましょう。 \[ \frac{dy}{dt} - ky = 0\] これは未知関数 \( y \) についての 1 階同次線形常微分方程式になります。マルサスモデルに現れる式です。 \[ \frac{d ^2 \theta}{dt^2} + \frac{g}{l} \sin \theta = 0\] これは未知関数 \( \theta \) についての 2 階同次非線形常微分方程式になります。単振り子の運動方程式です。 \[ mC \frac{d T}{dt} + aT = k + a T_e \] これは未知関数 \( T \) についての 1 階非同次線形常微分方程式になります。水が沸騰するまでの温度変化の予測に用いた式です。 \[ \frac{\partial c}{\partial t} - \frac{\partial ^2 c}{\partial x^2} = 0 \] これは未知関数 \( c \) についての 2 階同次線形偏微分方程式になります。1 次元拡散方程式です。
微分方程式に含まれる(偏)導関数の最高次数が \( n \) 次(偏)導関数であるとき、それを \( n \) 階の微分方程式といいます。
未知関数およびその(偏)導関数を独立変数 \( \mathfrak D \) とする一次関数の形からなる項 \[ a \mathfrak D \rm + \it b \] を考えます。ここで \( a \) および \( b \) は任意の既知関数とします。 このような項のみを含む微分方程式を線形といい、線形でないものを非線形といいます。
すべての項が未知関数およびその(偏)導関数を含むか 0 である微分方程式を同次といい、そうでないものを非同次といいます。
一般論だけだとわかりにくいので具体例を見てみましょう。 \[ \frac{dy}{dt} - ky = 0\] これは未知関数 \( y \) についての 1 階同次線形常微分方程式になります。マルサスモデルに現れる式です。 \[ \frac{d ^2 \theta}{dt^2} + \frac{g}{l} \sin \theta = 0\] これは未知関数 \( \theta \) についての 2 階同次非線形常微分方程式になります。単振り子の運動方程式です。 \[ mC \frac{d T}{dt} + aT = k + a T_e \] これは未知関数 \( T \) についての 1 階非同次線形常微分方程式になります。水が沸騰するまでの温度変化の予測に用いた式です。 \[ \frac{\partial c}{\partial t} - \frac{\partial ^2 c}{\partial x^2} = 0 \] これは未知関数 \( c \) についての 2 階同次線形偏微分方程式になります。1 次元拡散方程式です。
重ね合わせの原理
\[ 重ね合わせの原理\]
ある線形同次微分方程式を満たす2つの解 \( y_1 \) 、\( y_2 \) について、\( c_1 \) と \( c_2 \) を任意の定数とすると、
\[ c_1 y_1 + c_2 y_2\]
もこの線形同次微分方程式を満たす解である。これを重ね合わせの原理という。
重ね合わせの原理の証明は、
未知関数およびその(偏)導関数を表す変数 \( \mathfrak D \it _i \) により線形同次微分方程式を次のように表すことから始めます。
\[ \sum _{i=1} ^n A_i \mathfrak D \it _i \rm = 0 \ \ \ \ldots (1)\]
ここで \( A_i \) は任意の定数、\( n \) は任意の自然数です。
変数 \( \mathfrak D \it _i \) に具体的な解 \( y_1 \) および \( y_2 \) を当てはめたものを \( \mathfrak D \it _i \rm \left( \it y
\rm _1 \right) \) 、\( \mathfrak D \it _i \rm \left( \it y \rm _2 \right) \) とそれぞれ表すことにすると、
\[ \sum _{i=1} ^n A_i \mathfrak D \it _i \rm \left( \it y \rm _1 \right) = 0\]
\[ \sum _{i=1} ^n A_i \mathfrak D \it _i \rm \left( \it y \rm _2 \right) = 0\]
が成り立ちます。ゆえに、
\[ \begin{align}
\sum _{i=1} ^n A_i \mathfrak D \it _i \rm \left( \it c \rm _1 \it y \rm _1 + \it c \rm _2 \it y \rm _2
\right) &=
\sum _{i=1} ^n \left\{ A_i c_1 \mathfrak D \it _i \rm \left( \it y \rm _1 \right) + \it A_i c \rm _2
\mathfrak D \it _i \rm \left( \it y \rm _2 \right) \right\} \\\\
&= c_1 \sum _{i=1} ^n A_i \mathfrak D \it _i \rm \left( \it y \rm _1 \right) + \it c \rm _2 \it \sum _{
\it i \rm =1} \it ^n A_i \mathfrak D \it _i \rm \left( \it y \rm _2 \right) \\\\
&= 0
\end{align}\]
となります。1 行目の変形では定数倍と和・差の微分公式を用いています。以上より、\( y_1 \) と \( y_2 \) が \( (1) \) の解なら、
\[ c_1 y_1 + c_2 y_2\]
も \( (1) \) の解であるといえます。
重ね合わせの原理を用いると、線形同次微分方程式の解を初期条件や境界条件に適合するように拡張することが容易になります。
重ね合わせの原理を用いると、線形同次微分方程式の解を初期条件や境界条件に適合するように拡張することが容易になります。
参考:
[1] 和達三樹、物理のための数学 (物理入門コース10)、岩波書店、1983年3月14日発行