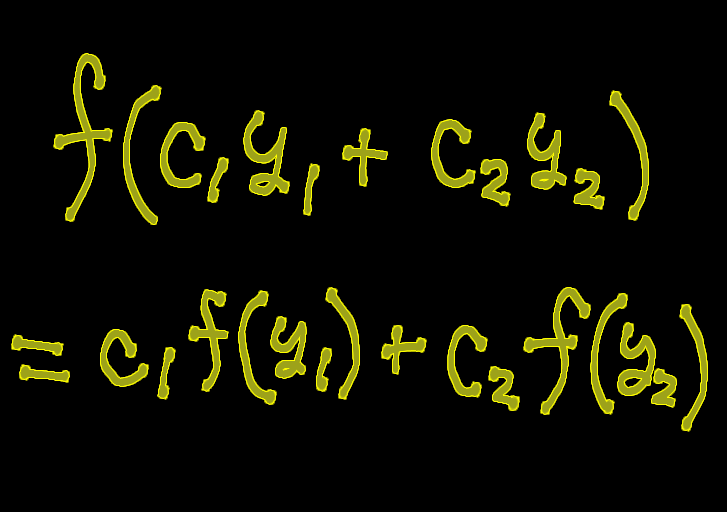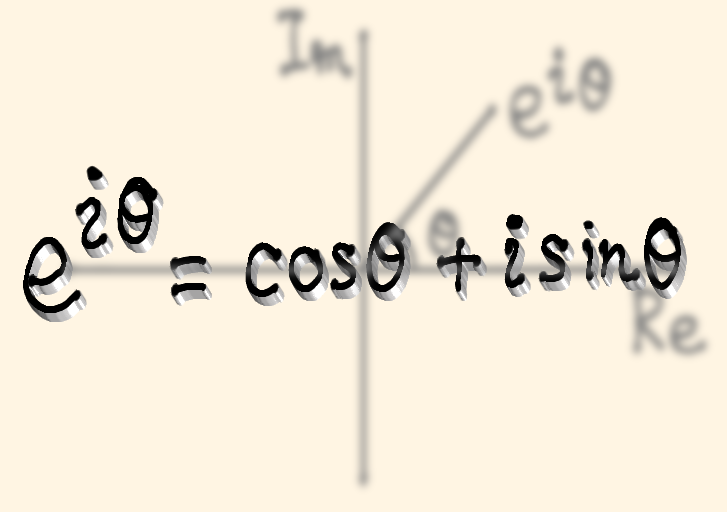
目次
・複素数
・複素平面
・共軛複素数
カヤ
今回は複素数について解説しよう。
複素数
\[ 複素数\]
\[ i = \sqrt{-1}\]
を虚数単位という。2 つの実数 \( a \) 、\( b \) と虚数単位 \( i \) を用いて
\[ c = a + bi = a + ib \]
という形で表される数 \( c \) を複素数という。
ここで、\( a \) を複素数 \( c \) の実部（実数部分）といい、\( b \) を複素数 \( c \) の虚部（虚数部分）という。
実部と虚部をそれぞれ、
\[ a = \rm Re \ \it c\]
\[ b = \rm Im \ \it c\]
と表す。実部が 0 である複素数
\[ c = ib \]
を純虚数という。
複素数は実数を拡張した数の概念です。
虚数単位 \( i \) を導入することで負の平方根を考えることができるようになり、例えば
\[ x^2 = -2\]
というような方程式にも解があるとみなすことができます。
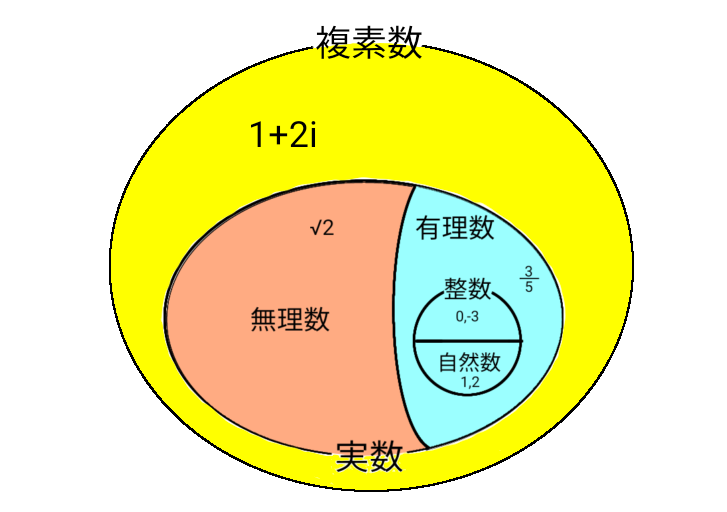
今まで扱ってきた自然数 \( \mathbb N \) 、整数 \( \mathbb Z \) 、有理数 \( \mathbb Q \) 、実数 \( \mathbb R \) 、そして複素数 \( \mathbb C \) という数の集合の間の包含関係は、 \[ \mathbb N \subset \mathbb Z \subset \mathbb Q \subset \mathbb R \subset \mathbb C \] となります。
複素数の相等関係と四則演算は次で定義されます。
今まで扱ってきた自然数 \( \mathbb N \) 、整数 \( \mathbb Z \) 、有理数 \( \mathbb Q \) 、実数 \( \mathbb R \) 、そして複素数 \( \mathbb C \) という数の集合の間の包含関係は、 \[ \mathbb N \subset \mathbb Z \subset \mathbb Q \subset \mathbb R \subset \mathbb C \] となります。
複素数の相等関係と四則演算は次で定義されます。
\[ 複素数の相等関係と四則演算\]
相等関係 \[ \begin{align} &1) \ \ a + ib = 0 \ \ \rm ならば \ \ \it a \rm = 0, \it b \rm = 0 \\\\ &2) \ \ a_1 + ib_1 = a_2 + ib_2 \ \ \rm ならば \ \ \it a \rm _1 = \it a \rm _2, \it b \rm _1 = \it b \rm _2 \end{align}\] 四則演算
和 \[ \left( a + ib \right) + \left( c + id \right) = \left( a + c \right) + i \left( b + d \right) \] 差 \[ \left( a + ib \right) - \left( c + id \right) = \left( a - c \right) + i \left( b - d \right) \] 積 \[ \begin{align} \left( a + ib \right) \left( c + id \right) &= ac + iad + ibc + i^2 bd \\\\ &= \left( ac - bd \right) + i \left( ad + bc \right) \end{align}\] 商 \[ \begin{align} \frac{a + ib}{c + id} &= \frac{a + ib}{c + id} \cdot \frac{c - id}{c - id} \\\\ &= \frac{ac + bd}{c^2 + d^2} + i \frac{bc - ad}{c^2 + d^2} \end{align}\] 以上の規則から、実数と同様に、複素数に対しても、
[1] 交換法則 \[ c_1 + c_2 = c_2 + c_1\] \[ c_1 c_2 = c_2 c_1\] [2] 結合法則 \[ \left( c_1 + c_2 \right) + c_3 = c_1 + \left( c_2 + c_3 \right) \] \[ \left( c_1 c_2 \right) c_3 = c_1 \left( c_2 c_3 \right)\] [3] 分配法則 \[ c_1 \left( c_2 + c_3 \right) = c_1 c_2 + c_1 c_3 \] が成り立つ。
相等関係 \[ \begin{align} &1) \ \ a + ib = 0 \ \ \rm ならば \ \ \it a \rm = 0, \it b \rm = 0 \\\\ &2) \ \ a_1 + ib_1 = a_2 + ib_2 \ \ \rm ならば \ \ \it a \rm _1 = \it a \rm _2, \it b \rm _1 = \it b \rm _2 \end{align}\] 四則演算
和 \[ \left( a + ib \right) + \left( c + id \right) = \left( a + c \right) + i \left( b + d \right) \] 差 \[ \left( a + ib \right) - \left( c + id \right) = \left( a - c \right) + i \left( b - d \right) \] 積 \[ \begin{align} \left( a + ib \right) \left( c + id \right) &= ac + iad + ibc + i^2 bd \\\\ &= \left( ac - bd \right) + i \left( ad + bc \right) \end{align}\] 商 \[ \begin{align} \frac{a + ib}{c + id} &= \frac{a + ib}{c + id} \cdot \frac{c - id}{c - id} \\\\ &= \frac{ac + bd}{c^2 + d^2} + i \frac{bc - ad}{c^2 + d^2} \end{align}\] 以上の規則から、実数と同様に、複素数に対しても、
[1] 交換法則 \[ c_1 + c_2 = c_2 + c_1\] \[ c_1 c_2 = c_2 c_1\] [2] 結合法則 \[ \left( c_1 + c_2 \right) + c_3 = c_1 + \left( c_2 + c_3 \right) \] \[ \left( c_1 c_2 \right) c_3 = c_1 \left( c_2 c_3 \right)\] [3] 分配法則 \[ c_1 \left( c_2 + c_3 \right) = c_1 c_2 + c_1 c_3 \] が成り立つ。
複素数の四則演算については、積は実部と虚部の区別なく行えますが、和と差は実部と虚部それぞれ別に計算することに注意しましょう。
虚数単位 \( i \) に注意して整理することが大切です。
それ以外は、商の計算が少しややこしいなどありますが、基本的に実数の四則演算と同様です。
カヤ
次は複素数を図示するための複素平面という手法について解説しよう。
複素平面
\[ 複素平面\]
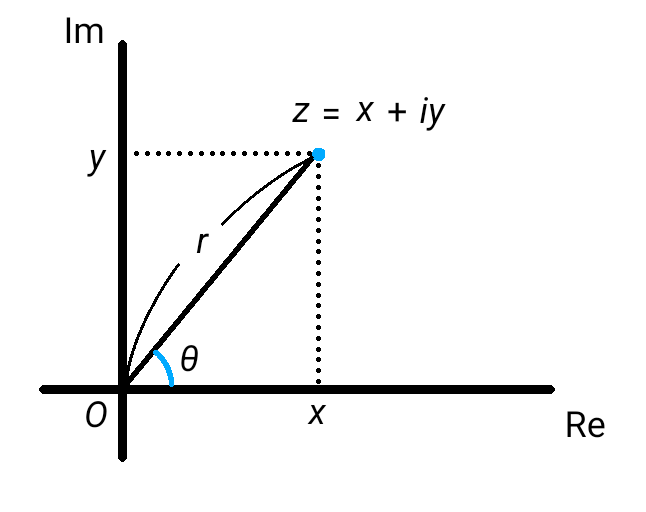
\( xy \) 座標平面上の座標が \( \left( x,y \right) \) である点と複素数 \( z = x + iy \)
を対応させたものを複素平面またはガウス平面という。
複素平面において、\( x \) 軸を実軸、\( y \) 軸を虚軸という。
複素平面において、原点 \( O \) と点 \( P \left( x,y \right) \) の距離を \( r \) 、線分 \( OP \) と \( x \) 軸の間の角を \( \theta \) とすれば、 \[ \begin{align} x &= r \cos \theta \\\\ y &= r \sin \theta \end{align}\] であるから、複素数 \( z \) は \[ z = r \left( \cos \theta + i \sin \theta \right) \] と書ける。これを、\( z \) の極形式といい、\( r \) を \( z \) の絶対値、\( \theta \) を \( z \) の偏角という。 \( z \) の絶対値を \( |z| \) 、\( z \) の偏角を \( \rm arg \ \it z \) と書く。つまり、 \[ |z| = r = \sqrt{x^2 + y^2} \] \[ \rm arg \ \it z \rm = \it \theta \] である。
複素平面において、原点 \( O \) と点 \( P \left( x,y \right) \) の距離を \( r \) 、線分 \( OP \) と \( x \) 軸の間の角を \( \theta \) とすれば、 \[ \begin{align} x &= r \cos \theta \\\\ y &= r \sin \theta \end{align}\] であるから、複素数 \( z \) は \[ z = r \left( \cos \theta + i \sin \theta \right) \] と書ける。これを、\( z \) の極形式といい、\( r \) を \( z \) の絶対値、\( \theta \) を \( z \) の偏角という。 \( z \) の絶対値を \( |z| \) 、\( z \) の偏角を \( \rm arg \ \it z \) と書く。つまり、 \[ |z| = r = \sqrt{x^2 + y^2} \] \[ \rm arg \ \it z \rm = \it \theta \] である。
実数は一つの直線でその値を表すことができましたが、複素数は実部と虚部に分かれているためこの値を表すには二つの直線で作られる平面が必要となります。
複素平面を図示すると下図のようになります。
ナユミ
一つの数を表すのに \( xy \) 座標平面を使うのはちょっと違和感あるわね。
カヤ
慣れは要るかもな。続いて、絶対値と偏角について成り立つ式を見ていこう。
\[ \begin{align}
絶対値と偏角に関する等式・不等式
\end{align}\]
2 つの複素数 \( z_1 \) と \( z_2 \) の絶対値および偏角について、次の式が成り立つ。
和・差 \[ \begin{align} \left| z_1 \pm z_2 \right| & \leq | z_1 | + | z_2 | \ \ \ \text{（等号は} \ \ \rm arg \ \it z \rm _1 \rm = arg \ \it z \rm _2 \ \text{のときだけ成立。）} \\\\ \end{align}\] 積 \[ \begin{align} | z_1 z_2 | &= | z_1 | | z_2 | \\\\ \rm arg \ \left( \it z \rm _1 \it z \rm _2 \right) &= \rm arg \ \it z \rm _1 + arg \ \it z \rm _2 \end{align}\] 商 \[ \begin{align} \left| \frac{z_1}{z_2} \right| &= \frac{| z_1 |}{| z_2 |} \\\\ \rm arg \ \left( \frac{\it z \rm _1}{\it z \rm _2} \right) &= \rm arg \ \it z \rm _1 - arg \ \it z \rm _2 \end{align}\]
和・差 \[ \begin{align} \left| z_1 \pm z_2 \right| & \leq | z_1 | + | z_2 | \ \ \ \text{（等号は} \ \ \rm arg \ \it z \rm _1 \rm = arg \ \it z \rm _2 \ \text{のときだけ成立。）} \\\\ \end{align}\] 積 \[ \begin{align} | z_1 z_2 | &= | z_1 | | z_2 | \\\\ \rm arg \ \left( \it z \rm _1 \it z \rm _2 \right) &= \rm arg \ \it z \rm _1 + arg \ \it z \rm _2 \end{align}\] 商 \[ \begin{align} \left| \frac{z_1}{z_2} \right| &= \frac{| z_1 |}{| z_2 |} \\\\ \rm arg \ \left( \frac{\it z \rm _1}{\it z \rm _2} \right) &= \rm arg \ \it z \rm _1 - arg \ \it z \rm _2 \end{align}\]
まず、絶対値の和と差についての不等式について考えます。
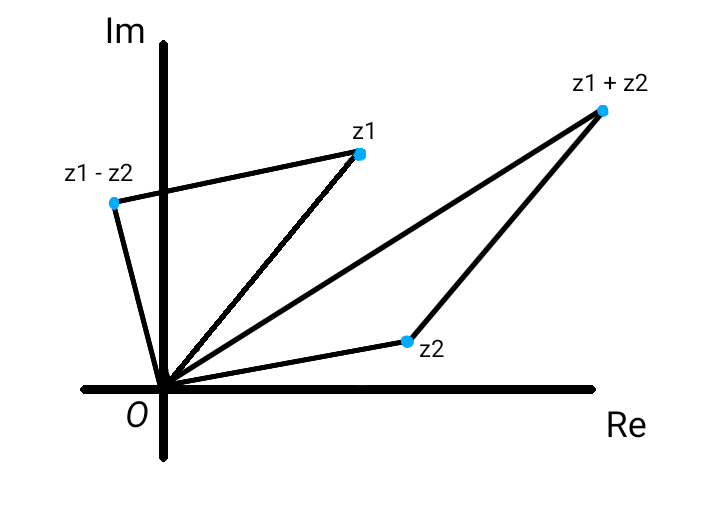
\( z_1 + z_2 \) を複素平面上に図示すると、これは点 \( z_2 \) から線分 \( Oz_1 \) と同じ長さの線分を \( O \) から \( z_1 \)
に向かう方向と同じ方向に伸ばしたところにあります。
このとき、三角形 \( Oz_2 \left( z_1 + z_2 \right) \) を考えると、\( \left| z_1 + z_2 \right| \) は辺 \( O \left( z_1 + z_2
\right) \) の長さであり、残りの 2 辺の長さは \( | z_1 | \) と \( | z_2 | \) になります。
三角形の 2 辺の和は他の 1 辺より大きいので、
\[ \begin{align}
\left| z_1 + z_2 \right| \lt | z_1 | + | z_2 |
\end{align}\]
が成り立ちます。\( \rm arg \ \it z \rm _1 \rm = arg \ \it z \rm _2 \) のときは、3 点 \( z_1 \) 、\( z_2 \) 、\( z_1 + z_2 \)
は同一直線上にあるので、
\[ \begin{align}
\left| z_1 + z_2 \right| = | z_1 | + | z_2 |
\end{align}\]
となります。同様に、\( z_1 - z_2 \) を複素平面上に図示すると、これは点 \( z_1 \) から線分 \( Oz_2 \) と同じ長さの線分を \( z_2 \) から \( O \)
に向かう方向と同じ方向に伸ばしたところにあります。
このとき、三角形 \( Oz_1 \left( z_1 - z_2 \right) \) を考えると、\( \left| z_1 - z_2 \right| \) は辺 \( O \left( z_1 - z_2
\right) \) の長さであり、残りの 2 辺の長さは \( | z_1 | \) と \( | z_2 | \) になります。
三角形の 2 辺の和は他の 1 辺より大きいので、
\[ \begin{align}
\left| z_1 - z_2 \right| \lt | z_1 | + | z_2 |
\end{align}\]
が成り立ちます。\( \rm arg \ \it z \rm _1 \rm = arg \ \it z \rm _2 \) のときは、3 点 \( z_1 \) 、\( z_2 \) 、\( z_1 - z_2 \)
は同一直線上にあるので、
\[ \begin{align}
\left| z_1 - z_2 \right| = | z_1 | + | z_2 |
\end{align}\]
となります。
続いて、積についての等式について考えます。
\[ \begin{align}
z_1 = r_1 \left( \cos \theta _1 + i \sin \theta _1 \right), \ z_2 = r_2 \left( \cos \theta _2 + i \sin \theta _2 \right)
\end{align}\]
とすると、
\[ \begin{align}
z_1 z_2 &= r_1 r_2 \left( \cos \theta _1 + i \sin \theta _1 \right) \left( \cos \theta _2 + i \sin \theta _2 \right) \\\\
&= r_1 r_2 \left( \cos \theta _1 \cos \theta _2 + i \cos \theta _1 \sin \theta _2 + i \sin \theta _1 \cos \theta _2 + i^2 \sin \theta _1 \sin \theta _2 \right) \\\\
&= r_1 r_2 \left\{ \left( \cos \theta _1 \cos \theta _2 - \sin \theta _1 \sin \theta _2 \right) + i \left( \sin \theta _1 \cos \theta _2 + \cos \theta _1 \sin \theta _2 \right) \right\} \\\\
&= r_1 r_2 \left\{ \cos \left( \theta _1 + \theta _2 \right) + i \sin \left( \theta _1 + \theta _2 \right)\right\}
\end{align}\]
となります。よって、
\[ \begin{align}
| z_1 z_2 | &= r_1 r_2
= | z_1 | | z_2 | \\\\
\rm arg \ \left( \it z \rm _1 \it z \rm _2 \right) &= \theta _1 + \theta _2
= \rm arg \ \it z \rm _1 + arg \ \it z \rm _2
\end{align}\]
となります。
同じく、商についての等式について考えると、 \[ \begin{align} \frac{z_1}{z_2} &= \frac{r_1}{r_2} \cdot \frac{\cos \theta _1 + i \sin \theta _1}{\cos \theta _2 + i \sin \theta _2} \\\\ &= \frac{r_1}{r_2} \cdot \frac{\left( \cos \theta _1 + i \sin \theta _1 \right) \left( \cos \theta _2 - i \sin \theta _2 \right)}{\left( \cos \theta _2 + i \sin \theta _2 \right) \left( \cos \theta _2 - i \sin \theta _2 \right)} \\\\ &= \frac{r_1}{r_2} \cdot \frac{\cos \theta _1 \cos \theta _2 - i \cos \theta _1 \sin \theta _2 + i \sin \theta _1 \cos \theta _2 - i^2 \sin \theta _1 \sin \theta _2 }{\cos ^2 \theta _2 - i^2 \sin ^2 \theta _2 } \\\\ &= \frac{r_1}{r_2} \cdot \frac{\left( \cos \theta _1 \cos \theta _2 + \sin \theta _1 \sin \theta _2 \right) + i \left( \sin \theta _1 \cos \theta _2 - \cos \theta _1 \sin \theta _2\right)}{\cos ^2 \theta _2 + \sin ^2 \theta _2 } \\\\ &= \frac{r_1}{r_2} \left\{ \cos \left( \theta _1 - \theta _2\right) + i \sin \left( \theta _1 - \theta _2\right) \right\} \end{align}\] となります。よって、 \[ \begin{align} \left| \frac{z_1}{z_2} \right| &= \frac{r_1}{r_2} = \frac{| z_1 |}{| z_2 |} \\\\ \rm arg \ \left( \frac{\it z \rm _1}{\it z \rm _2} \right) &= \theta _1 - \theta _2 = \rm arg \ \it z \rm _1 - arg \ \it z \rm _2 \end{align}\] となります。
同じく、商についての等式について考えると、 \[ \begin{align} \frac{z_1}{z_2} &= \frac{r_1}{r_2} \cdot \frac{\cos \theta _1 + i \sin \theta _1}{\cos \theta _2 + i \sin \theta _2} \\\\ &= \frac{r_1}{r_2} \cdot \frac{\left( \cos \theta _1 + i \sin \theta _1 \right) \left( \cos \theta _2 - i \sin \theta _2 \right)}{\left( \cos \theta _2 + i \sin \theta _2 \right) \left( \cos \theta _2 - i \sin \theta _2 \right)} \\\\ &= \frac{r_1}{r_2} \cdot \frac{\cos \theta _1 \cos \theta _2 - i \cos \theta _1 \sin \theta _2 + i \sin \theta _1 \cos \theta _2 - i^2 \sin \theta _1 \sin \theta _2 }{\cos ^2 \theta _2 - i^2 \sin ^2 \theta _2 } \\\\ &= \frac{r_1}{r_2} \cdot \frac{\left( \cos \theta _1 \cos \theta _2 + \sin \theta _1 \sin \theta _2 \right) + i \left( \sin \theta _1 \cos \theta _2 - \cos \theta _1 \sin \theta _2\right)}{\cos ^2 \theta _2 + \sin ^2 \theta _2 } \\\\ &= \frac{r_1}{r_2} \left\{ \cos \left( \theta _1 - \theta _2\right) + i \sin \left( \theta _1 - \theta _2\right) \right\} \end{align}\] となります。よって、 \[ \begin{align} \left| \frac{z_1}{z_2} \right| &= \frac{r_1}{r_2} = \frac{| z_1 |}{| z_2 |} \\\\ \rm arg \ \left( \frac{\it z \rm _1}{\it z \rm _2} \right) &= \theta _1 - \theta _2 = \rm arg \ \it z \rm _1 - arg \ \it z \rm _2 \end{align}\] となります。
ナユミ
加法定理を上手く使っているわね。
カヤ
そうだな。最後に共軛複素数というものについて説明しておこう。
共軛複素数
\[ 共軛複素数\]
複素数 \( z = x + iy \) に対して、\( x - iy \) を \( z \) の共軛複素数といい、\( z^* = x
- iy \) と表す。
複素平面において、\( z \) と \( z^* \) は \( x \) 軸に対して線対称の位置にある。また、\( z \) と \( z^* \) との積は実数であり、\( z \)
の絶対値の2乗に等しい。
\[ \begin{align}
zz^* &= \left( x + iy \right) \left( x - iy \right) \\\\
&= x^2 + y^2 \\\\
&= |z|^2
\end{align}\]
軛は「くびき」とも読み、牛車の先端部にある牛の首にかける横木を意味します。
共軛というのは「軛を共にして車を引く」の意味で、二つの対象の間に特別な関係があることを指しています。
カヤ
実数を複素数に拡張することで、数の世界は大きく広がるんだ。とっつきにくいかもしれないがとりあえず頭に置いておくといいぞ。
ナユミ
わかったわ。
参考：
[1] 和達三樹、物理のための数学 （物理入門コース10）、岩波書店、1983年3月14日発行
[2] 新村出、広辞苑 第六版、岩波書店、2008年1月11日発行
前の記事
第25話
重ね合わせの原理
重ね合わせの原理
次の記事
第27話
オイラーの公式
オイラーの公式