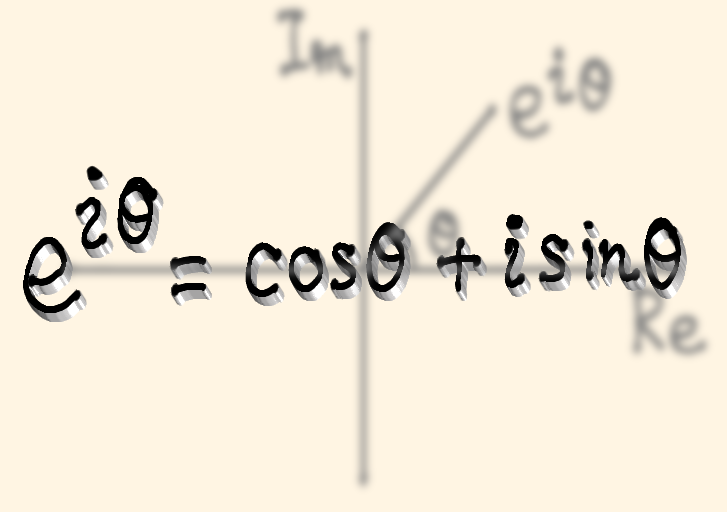
目次
・ド・モアブルの定理
・オイラーの公式
・三角関数の表現
ド・モアブルの定理
\[ ド・モアブルの定理\]
\( n \) を整数、\( \theta \) を実数、\( i \) を虚数単位として、
\[ \cos n \theta + i \sin n \theta = \left( \cos \theta + i \sin \theta \right)^n \ \ \ \ldots (*1) \]
が成り立つ。これをド・モアブルの定理という。
この定理は数学的帰納法により証明できます。
まずは、\( n \geq 0 \) の場合を示します。
[1] \( n = 0 \) のとき \[ \cos 0 + i \sin 0 = 1\] \[ \left( \cos 0 + i \sin 0 \right)^0 = 1^0 = 1\] よって、\( \left( *1 \right) \) は成り立つ。
[2] \( n = k \) のとき、\( \left( *1 \right) \) が成り立つと仮定すると、 \[ \begin{align} \left( \cos \theta + i \sin \theta \right)^{k+1} &= \left( \cos k \theta + i \sin k \theta \right) \left( \cos \theta + i \sin \theta \right) \\\\ &= \left( \cos k \theta \cos \theta - \sin k \theta \sin \theta \right) + i \left( \sin k \theta \cos \theta + \cos k \theta \sin \theta \right) \\\\ &= \cos \left( k + 1 \right) \theta + i \sin \left( k + 1 \right) \theta \end{align}\] ゆえに、\( n = k + 1\) のときも、\( \left( *1 \right) \) が成り立つ。
[1]と[2]より、\( n \geq 0 \) なる整数 \( n \) について \( \left( *1 \right) \) は成り立つ。
続いて、\( n \lt 0 \) の場合を示します。
\( m=-n \) とおくと、\( m \) は自然数であるから、\( \left( *1 \right) \) が成り立つ。よって、 \[ \begin{align} \left( \cos \theta + i \sin \theta \right)^{n} &= \frac{1}{\left( \cos \theta + i \sin \theta \right)^{m}} \\\\ &= \frac{1}{\cos m \theta + i \sin m \theta } \\\\ &= \frac{1}{\cos (-n) \theta + i \sin (-n) \theta } \\\\ &= \frac{1}{\cos n \theta - i \sin n \theta } \\\\ &= \frac{ \cos n \theta + i \sin n \theta}{\left( \cos n \theta - i \sin n \theta \right) \left( \cos n \theta + i \sin n \theta \right) } \\\\ &= \frac{ \cos n \theta + i \sin n \theta}{ \cos ^2 n \theta + \sin ^2 n \theta } \\\\ &= \cos n \theta + i \sin n \theta \end{align}\] ゆえに、\( n \lt 0 \) なる整数 \( n \) についても \( \left( *1 \right) \) は成り立つ。
以上より、すべての整数 \( n \) について、\( \left( *1 \right) \) は成り立つ。
まずは、\( n \geq 0 \) の場合を示します。
[1] \( n = 0 \) のとき \[ \cos 0 + i \sin 0 = 1\] \[ \left( \cos 0 + i \sin 0 \right)^0 = 1^0 = 1\] よって、\( \left( *1 \right) \) は成り立つ。
[2] \( n = k \) のとき、\( \left( *1 \right) \) が成り立つと仮定すると、 \[ \begin{align} \left( \cos \theta + i \sin \theta \right)^{k+1} &= \left( \cos k \theta + i \sin k \theta \right) \left( \cos \theta + i \sin \theta \right) \\\\ &= \left( \cos k \theta \cos \theta - \sin k \theta \sin \theta \right) + i \left( \sin k \theta \cos \theta + \cos k \theta \sin \theta \right) \\\\ &= \cos \left( k + 1 \right) \theta + i \sin \left( k + 1 \right) \theta \end{align}\] ゆえに、\( n = k + 1\) のときも、\( \left( *1 \right) \) が成り立つ。
[1]と[2]より、\( n \geq 0 \) なる整数 \( n \) について \( \left( *1 \right) \) は成り立つ。
続いて、\( n \lt 0 \) の場合を示します。
\( m=-n \) とおくと、\( m \) は自然数であるから、\( \left( *1 \right) \) が成り立つ。よって、 \[ \begin{align} \left( \cos \theta + i \sin \theta \right)^{n} &= \frac{1}{\left( \cos \theta + i \sin \theta \right)^{m}} \\\\ &= \frac{1}{\cos m \theta + i \sin m \theta } \\\\ &= \frac{1}{\cos (-n) \theta + i \sin (-n) \theta } \\\\ &= \frac{1}{\cos n \theta - i \sin n \theta } \\\\ &= \frac{ \cos n \theta + i \sin n \theta}{\left( \cos n \theta - i \sin n \theta \right) \left( \cos n \theta + i \sin n \theta \right) } \\\\ &= \frac{ \cos n \theta + i \sin n \theta}{ \cos ^2 n \theta + \sin ^2 n \theta } \\\\ &= \cos n \theta + i \sin n \theta \end{align}\] ゆえに、\( n \lt 0 \) なる整数 \( n \) についても \( \left( *1 \right) \) は成り立つ。
以上より、すべての整数 \( n \) について、\( \left( *1 \right) \) は成り立つ。
オイラーの公式
\[ オイラーの公式\]
\( i \) を虚数単位、\( \theta \) を実数として、
\[ e^{i \theta} = \cos \theta + i \sin \theta \]
が成り立つ。これをオイラーの公式という。
オイラーの公式は虚数単位 \( i \) を介して指数関数と三角関数を結びつける式です。
この公式の証明は次の通りです。
まず、ド・モアブルの定理 \[ \cos n \phi + i \sin n \phi = \left( \cos \phi + i \sin \phi \right)^n \] において、\( n \phi = \theta \) とおくと、 \[ \begin{align} \cos \theta + i \sin \theta = \left( \cos \frac{\theta}{n} + i \sin \frac{\theta}{n} \right)^n \end{align}\] ここで、\( n \) が \( \theta \) に比して十分に大きい自然数とすれば、次の近似が成り立つ。 \[ \cos \frac{\theta}{n} \cong \cos 0 = 1\] \[ \sin \frac{\theta}{n} \cong \frac{\theta}{n}\] よって、 \[ \begin{align} \cos \theta + i \sin \theta = \left( 1 + \frac{i \theta}{n} \right)^n \ \ \ \ldots (1) \end{align}\] ここで、指数関数についての極限公式 \[ \lim _{x \to 0} \frac{e^x - 1}{x} = 1\] において、\( x = i \theta / n \) とおけば、 \[ x \to 0 \rm \ \ ならば \ \ \it n \to \infty\] であるから、 \[ \begin{align} & \lim _{n \to \infty} \frac{e^{\frac{i \theta}{n}} - 1}{\frac{i \theta}{n}} = 1 \\\\ & \lim _{n \to \infty} e^{\frac{i \theta}{n}} = \lim _{n \to \infty} 1 + \frac{i \theta}{n} \\\\ & e^{i \theta} = \lim _{n \to \infty} \left( 1 + \frac{i \theta}{n} \right)^n \\\\ \end{align}\] よって、\( (1) \) 式において、右辺の \( n \to \infty \) の極限をとれば、 \[ \cos \theta + i \sin \theta = e^{i \theta}\] となり、オイラーの公式が成り立つことがわかる。
まず、ド・モアブルの定理 \[ \cos n \phi + i \sin n \phi = \left( \cos \phi + i \sin \phi \right)^n \] において、\( n \phi = \theta \) とおくと、 \[ \begin{align} \cos \theta + i \sin \theta = \left( \cos \frac{\theta}{n} + i \sin \frac{\theta}{n} \right)^n \end{align}\] ここで、\( n \) が \( \theta \) に比して十分に大きい自然数とすれば、次の近似が成り立つ。 \[ \cos \frac{\theta}{n} \cong \cos 0 = 1\] \[ \sin \frac{\theta}{n} \cong \frac{\theta}{n}\] よって、 \[ \begin{align} \cos \theta + i \sin \theta = \left( 1 + \frac{i \theta}{n} \right)^n \ \ \ \ldots (1) \end{align}\] ここで、指数関数についての極限公式 \[ \lim _{x \to 0} \frac{e^x - 1}{x} = 1\] において、\( x = i \theta / n \) とおけば、 \[ x \to 0 \rm \ \ ならば \ \ \it n \to \infty\] であるから、 \[ \begin{align} & \lim _{n \to \infty} \frac{e^{\frac{i \theta}{n}} - 1}{\frac{i \theta}{n}} = 1 \\\\ & \lim _{n \to \infty} e^{\frac{i \theta}{n}} = \lim _{n \to \infty} 1 + \frac{i \theta}{n} \\\\ & e^{i \theta} = \lim _{n \to \infty} \left( 1 + \frac{i \theta}{n} \right)^n \\\\ \end{align}\] よって、\( (1) \) 式において、右辺の \( n \to \infty \) の極限をとれば、 \[ \cos \theta + i \sin \theta = e^{i \theta}\] となり、オイラーの公式が成り立つことがわかる。
三角関数の表現
オイラーの公式を用いて三角関数を指数関数で表す方法を説明します。まずは、オイラーの公式から次の二つの式
\[ \begin{align}
e^{i \theta} &= \cos \theta + i \sin \theta \\\\
e^{-i \theta} &= \cos \theta - i \sin \theta
\end{align}\]
が成り立ちます。二つの式の両辺を足してから \( 2 \) で割ると、
\[ \begin{align}
\cos \theta = \frac{e^{i \theta} + e^{-i \theta}}{2}
\end{align}\]
を得ます。また、二つの式の両辺を引いてから \( 2i \) で割ると、
\[ \begin{align}
\sin \theta = \frac{e^{i \theta} - e^{-i \theta}}{2i}
\end{align}\]
を得ます。さらに、
\[ \begin{align}
\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{1}{i} \frac{e^{i \theta} - e^{-i \theta}}{e^{i
\theta} + e^{-i \theta}}
\end{align}\]
も成り立ちます。
参考:
[1] 和達三樹、物理のための数学 (物理入門コース10)、岩波書店、1983年3月14日発行
[2] Wikipedia ド・モアブルの定理、https://ja.wikipedia.org/wiki/ド・モアブルの定理、2024年4月12日閲覧
[3] Wikipedia オイラーの公式、https://ja.wikipedia.org/wiki/オイラーの公式、2024年4月12日閲覧