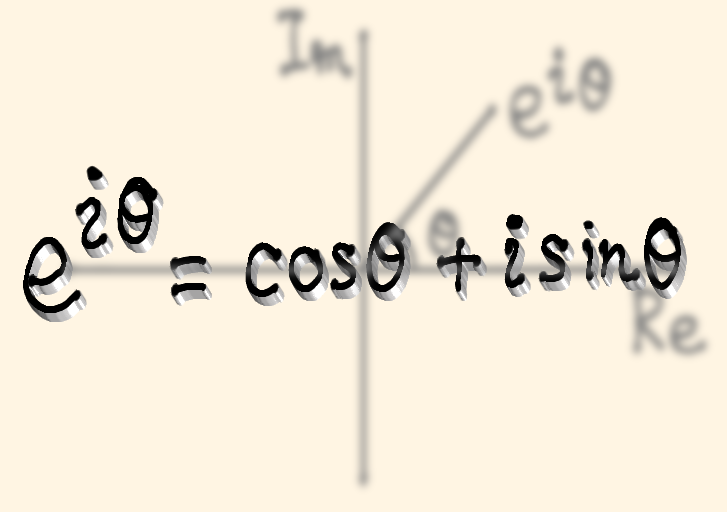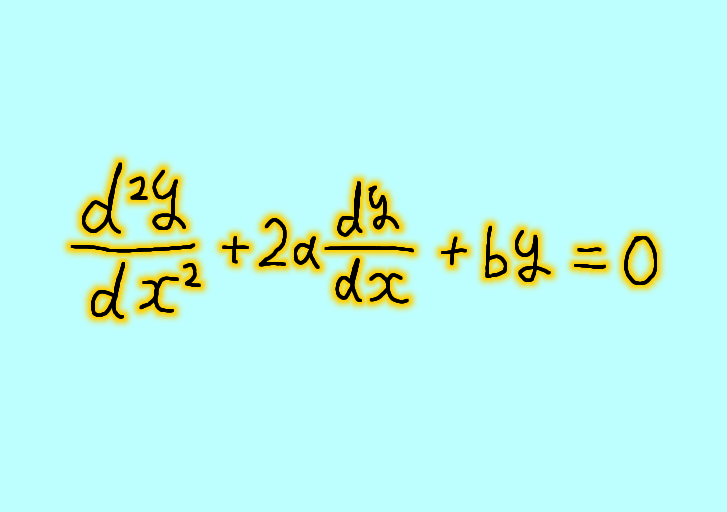
目次
・定数係数2階同次線形常微分方程式
定数係数2階同次線形常微分方程式
定数係数2階同次線形常微分方程式は一般に次の形で書くことができます。
\[ \frac{d^2 y}{dx^2} + 2a \frac{dy}{dx} + by = 0 \ \ \ \ldots (1) \]
ここで、\( a \) 、\( b \) は実数定数とします。
\( (1) \) 式を解くにあたり、まずは解を \[ y = e^{\lambda x}\] とおきます。これを \( (1) \) 式に代入します。 \[ \begin{align} \frac{d^2}{dx^2} \left( e^{\lambda x} \right) + 2a \frac{d}{dx} \left( e^{\lambda x} \right) + b \left( e^{\lambda x} \right) &= 0 \\\\ e^{\lambda x} \left( \lambda ^2 + 2a \lambda + b \right) &= 0 \end{align}\] ここで、\( e^{\lambda x} \neq 0 \) であるため、次式が成り立ちます。 \[ \lambda ^2 + 2a \lambda + b = 0 \ \ \ \ldots (2)\] \( (2) \) 式を特性方程式と呼びます。\( \lambda \) が特性方程式の解であれば、\( y = e^{\lambda x} \) は \( (1) \) 式の解となります。 そこで、\( (2) \) 式を満たす \( \lambda \) を求めます。 \[ \begin{align} \lambda ^2 + 2a \lambda + b &= 0 \\\\ \left( \lambda + a \right) ^2 &= a^2 -b \\\\ \lambda &= -a \pm \sqrt{a^2 -b} \ \ \ \ldots (3) \end{align}\] \( (3) \) 式の根号内の値により、\( (2) \) 式を満たす 2 つの解を \[ \begin{align} \lambda _1 = -a + \sqrt{a^2 -b} \\\\ \lambda _2 = -a - \sqrt{a^2 -b} \end{align}\] とすれば、
[1] \( a^2 -b \gt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる実数
[2] \( a^2 -b = 0 \) ならば \( \lambda _1 = \lambda _2 \) で実数
[3] \( a^2 -b \lt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる複素数
という三つのパターンがあります。以下それぞれの場合について説明します。
\( (1) \) 式を解くにあたり、まずは解を \[ y = e^{\lambda x}\] とおきます。これを \( (1) \) 式に代入します。 \[ \begin{align} \frac{d^2}{dx^2} \left( e^{\lambda x} \right) + 2a \frac{d}{dx} \left( e^{\lambda x} \right) + b \left( e^{\lambda x} \right) &= 0 \\\\ e^{\lambda x} \left( \lambda ^2 + 2a \lambda + b \right) &= 0 \end{align}\] ここで、\( e^{\lambda x} \neq 0 \) であるため、次式が成り立ちます。 \[ \lambda ^2 + 2a \lambda + b = 0 \ \ \ \ldots (2)\] \( (2) \) 式を特性方程式と呼びます。\( \lambda \) が特性方程式の解であれば、\( y = e^{\lambda x} \) は \( (1) \) 式の解となります。 そこで、\( (2) \) 式を満たす \( \lambda \) を求めます。 \[ \begin{align} \lambda ^2 + 2a \lambda + b &= 0 \\\\ \left( \lambda + a \right) ^2 &= a^2 -b \\\\ \lambda &= -a \pm \sqrt{a^2 -b} \ \ \ \ldots (3) \end{align}\] \( (3) \) 式の根号内の値により、\( (2) \) 式を満たす 2 つの解を \[ \begin{align} \lambda _1 = -a + \sqrt{a^2 -b} \\\\ \lambda _2 = -a - \sqrt{a^2 -b} \end{align}\] とすれば、
[1] \( a^2 -b \gt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる実数
[2] \( a^2 -b = 0 \) ならば \( \lambda _1 = \lambda _2 \) で実数
[3] \( a^2 -b \lt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる複素数
という三つのパターンがあります。以下それぞれの場合について説明します。
[1] \( a^2 -b \gt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる実数
\( y = e^{\lambda _1 x} \) と \( y = e^{\lambda _2 x} \) は \( (1) \) 式の解であるので、\( c_1 \) 、\( c_2 \) を任意の定数とすれば、重ね合わせの原理より \( (1) \) 式の一般解は次式で与えられます。 \[ \begin{align} y = c_1 e^{\lambda _1 x} + c_2 e^{\lambda _2 x} \end{align}\] [2] \( a^2 -b = 0 \) ならば \( \lambda _1 = \lambda _2 \) で実数
\( \lambda _1 = \lambda _2 = -a \) であり、\( y = e^{-a x} \) は \( (1) \) 式の解です。 これに加えて、\( y = xe^{-a x} \) も \( (1) \) を満たす解であることが以下のように確かめられます。 \[ \begin{align} & \frac{d^2}{dx^2} \left( xe^{-a x} \right) + 2a \frac{d}{dx} \left( xe^{-a x} \right) + b \left( xe^{-a x} \right) \\\\ = & \frac{d}{dx} \left( e^{-a x} - axe^{-a x} \right) + 2a \left( e^{-a x} - axe^{-a x} \right) + b xe^{-a x} \\\\ = & -2ae^{-a x} + a^2 xe^{-a x} + 2a \left( e^{-a x} - axe^{-a x} \right) + b xe^{-a x} \\\\ = & -a^2 xe^{-a x} + b xe^{-a x} \\\\ = & -b xe^{-a x} + b xe^{-a x} = 0 \end{align}\] したがって、\( c_1 \) 、\( c_2 \) を任意の定数とすれば、重ね合わせの原理より \( (1) \) 式の一般解は次式で与えられます。 \[ \begin{align} y = \left( c_1 + c_2 x \right) e^{-a x} \end{align}\] [3] \( a^2 -b \lt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる複素数
この場合、 \[ \begin{align} \lambda _1 &= -a + i \sqrt{b - a^2} \\\\ \lambda _2 &= -a - i \sqrt{b - a^2} \end{align}\] となり、 \[ \begin{align} y &= e^{\left( -a + i \sqrt{b - a^2} \right) x} \\\\ y &= e^{\left( -a - i \sqrt{b - a^2} \right) x} \end{align}\] は \( (1) \) 式の解です。したがって、\( c_1 \) 、\( c_2 \) を任意の定数とすれば、重ね合わせの原理より \( (1) \) 式の一般解は次式で与えられます。 \[ \begin{align} y = c_1 e^{\left( -a + i \sqrt{b - a^2} \right) x} + c_2 e^{\left( -a - i \sqrt{b - a^2} \right) x} \end{align}\] この一般解は複素数の値を取ることがありますが、多くの数理モデルで問題となるのは実数の値です。 そこで、この一般解をオイラーの公式 \[ \begin{align} e^{ix} = \cos x + i \sin x \end{align}\] を用いて次のように変形します。 \[ \begin{align} y &= c_1 e^{\left( -a + i \sqrt{b - a^2} \right) x} + c_2 e^{\left( -a - i \sqrt{b - a^2} \right) x} \\\\ &= c_1 e^{-ax} e^{i \sqrt{b - a^2} x} + c_2 e^{-ax} e^{- i \sqrt{b - a^2} x} \\\\ &= e^{-ax} \left( c_1 e^{i \sqrt{b - a^2} x} + c_2 e^{- i \sqrt{b - a^2} x} \right) \\\\ &= e^{-ax} \left\{ c_1 \left( \cos \sqrt{b - a^2} x + i \sin \sqrt{b - a^2} x \right) + c_2 \left( \cos \left( - \sqrt{b - a^2} x \right) + i \sin \left( - \sqrt{b - a^2} x \right) \right) \right\} \\\\ &= e^{-ax} \left\{ c_1 \left( \cos \sqrt{b - a^2} x + i \sin \sqrt{b - a^2} x \right) + c_2 \left( \cos \sqrt{b - a^2} x - i \sin \sqrt{b - a^2} x \right) \right\} \\\\ &= e^{-ax} \left\{ \left( c_1 + c_2 \right) \cos \sqrt{b - a^2} x + i \left( c_1 - c_2 \right) \sin \sqrt{b - a^2} x \right\} \\\\ &= e^{-ax} \left( A \cos \sqrt{b - a^2} x + B \sin \sqrt{b - a^2} x \right) \end{align}\] 最終行では、 \[ \begin{align} A &= c_1 + c_2 \\\\ B &= i \left( c_1 - c_2 \right) \end{align}\] と定数を置きなおしました。最終行の形式を用いれば、解の値を実数値に限って考えることができます。
\( y = e^{\lambda _1 x} \) と \( y = e^{\lambda _2 x} \) は \( (1) \) 式の解であるので、\( c_1 \) 、\( c_2 \) を任意の定数とすれば、重ね合わせの原理より \( (1) \) 式の一般解は次式で与えられます。 \[ \begin{align} y = c_1 e^{\lambda _1 x} + c_2 e^{\lambda _2 x} \end{align}\] [2] \( a^2 -b = 0 \) ならば \( \lambda _1 = \lambda _2 \) で実数
\( \lambda _1 = \lambda _2 = -a \) であり、\( y = e^{-a x} \) は \( (1) \) 式の解です。 これに加えて、\( y = xe^{-a x} \) も \( (1) \) を満たす解であることが以下のように確かめられます。 \[ \begin{align} & \frac{d^2}{dx^2} \left( xe^{-a x} \right) + 2a \frac{d}{dx} \left( xe^{-a x} \right) + b \left( xe^{-a x} \right) \\\\ = & \frac{d}{dx} \left( e^{-a x} - axe^{-a x} \right) + 2a \left( e^{-a x} - axe^{-a x} \right) + b xe^{-a x} \\\\ = & -2ae^{-a x} + a^2 xe^{-a x} + 2a \left( e^{-a x} - axe^{-a x} \right) + b xe^{-a x} \\\\ = & -a^2 xe^{-a x} + b xe^{-a x} \\\\ = & -b xe^{-a x} + b xe^{-a x} = 0 \end{align}\] したがって、\( c_1 \) 、\( c_2 \) を任意の定数とすれば、重ね合わせの原理より \( (1) \) 式の一般解は次式で与えられます。 \[ \begin{align} y = \left( c_1 + c_2 x \right) e^{-a x} \end{align}\] [3] \( a^2 -b \lt 0 \) ならば \( \lambda _1 \) と \( \lambda _2 \) は相異なる複素数
この場合、 \[ \begin{align} \lambda _1 &= -a + i \sqrt{b - a^2} \\\\ \lambda _2 &= -a - i \sqrt{b - a^2} \end{align}\] となり、 \[ \begin{align} y &= e^{\left( -a + i \sqrt{b - a^2} \right) x} \\\\ y &= e^{\left( -a - i \sqrt{b - a^2} \right) x} \end{align}\] は \( (1) \) 式の解です。したがって、\( c_1 \) 、\( c_2 \) を任意の定数とすれば、重ね合わせの原理より \( (1) \) 式の一般解は次式で与えられます。 \[ \begin{align} y = c_1 e^{\left( -a + i \sqrt{b - a^2} \right) x} + c_2 e^{\left( -a - i \sqrt{b - a^2} \right) x} \end{align}\] この一般解は複素数の値を取ることがありますが、多くの数理モデルで問題となるのは実数の値です。 そこで、この一般解をオイラーの公式 \[ \begin{align} e^{ix} = \cos x + i \sin x \end{align}\] を用いて次のように変形します。 \[ \begin{align} y &= c_1 e^{\left( -a + i \sqrt{b - a^2} \right) x} + c_2 e^{\left( -a - i \sqrt{b - a^2} \right) x} \\\\ &= c_1 e^{-ax} e^{i \sqrt{b - a^2} x} + c_2 e^{-ax} e^{- i \sqrt{b - a^2} x} \\\\ &= e^{-ax} \left( c_1 e^{i \sqrt{b - a^2} x} + c_2 e^{- i \sqrt{b - a^2} x} \right) \\\\ &= e^{-ax} \left\{ c_1 \left( \cos \sqrt{b - a^2} x + i \sin \sqrt{b - a^2} x \right) + c_2 \left( \cos \left( - \sqrt{b - a^2} x \right) + i \sin \left( - \sqrt{b - a^2} x \right) \right) \right\} \\\\ &= e^{-ax} \left\{ c_1 \left( \cos \sqrt{b - a^2} x + i \sin \sqrt{b - a^2} x \right) + c_2 \left( \cos \sqrt{b - a^2} x - i \sin \sqrt{b - a^2} x \right) \right\} \\\\ &= e^{-ax} \left\{ \left( c_1 + c_2 \right) \cos \sqrt{b - a^2} x + i \left( c_1 - c_2 \right) \sin \sqrt{b - a^2} x \right\} \\\\ &= e^{-ax} \left( A \cos \sqrt{b - a^2} x + B \sin \sqrt{b - a^2} x \right) \end{align}\] 最終行では、 \[ \begin{align} A &= c_1 + c_2 \\\\ B &= i \left( c_1 - c_2 \right) \end{align}\] と定数を置きなおしました。最終行の形式を用いれば、解の値を実数値に限って考えることができます。
参考:
[1] 和達三樹、物理のための数学 (物理入門コース10)、岩波書店、1983年3月14日発行