目次
・水の加熱と温度変化
・水の加熱実験
ナユミ
えー、これ台風直撃じゃない。買い物明日行っとかなきゃなあ…、あっ、ドタドタ…
カヤ
大丈夫、ナユ姉？
ナユミ
うん、セーフよ。夏は煮立つのが速くて油断できないわね。
カヤ
そうだな。加熱中のスマホもほどほどにな。
ナユミ
そんなに心配しなくても大丈夫よ。それにしても、どうして夏は煮立つのが速いのかしら？
カヤ
それはまあ、室温が高いからだろうけど…。どれ、一つモデルでも立ててみるかな。
水の加熱と温度変化
ナユミ
どうやってモデル化するの？
カヤ
まずは、中学理科で習う次のことについて知っておく必要があるな。
\[ 熱量と比熱の関係式\]
\[ q = m C \Delta T \]
\( q \) ：物質が得た熱量、\( m \) ：物質の質量、\( C \) ：物質の比熱、\( \Delta T \) ：物質の温度変化
物質は与えられた熱量に比例して温度が上昇します。
同じ物質でも、たくさんあると、つまり質量が大きいと、温度を上げるために必要な熱の量も多くなります。
比熱は単位質量の物質の温度を1℃上げるのに必要な熱量です。
ナユミ
この式をどう使っていけばいいのかしら？
カヤ
モデル化にはもう少し準備が必要だな。次は、さっきの式の右辺 \( q \) について詳しく考えていこう。
ガスコンロで鍋に入れた水を温めているとき、水はコンロの火から熱を得ます。
一方、温められた水の熱の一部は周りの空気へと逃げていきます。
これらの効果を先ほどの式に組み込み、微分方程式を作っていきます。
まずは、先の式を両辺短い時間区間 \( \Delta t \) で割ります。
\[ \frac{q}{\Delta t} = m C \frac{\Delta T}{\Delta t} \]
\( \Delta t \) ：短い時間区間
この式の左辺は熱の移動量の平均速度を表しています。
コンロの火から熱をもらう速度はコンロの火の強さによって決まり、
火の強さはコンロのレバーを動かさない限り変わらないので、これは定数 \( k \) と置いてよさそうです。
また、周りの空気に逃げていく熱についてですが、これは周りの空気の温度と鍋の中の水の温度との温度差に比例した速度で熱が逃げていくと仮定します。
これらの仮定のもと、左辺を書き換えると次のようになります。
\[ k - a \left( T - T_{e} \right) = m C \frac{\Delta T}{\Delta t} \]
\( k \) ：コンロの火から受ける熱量の平均速度、\( a \) ：正の比例定数、\( T \) ：鍋の中の水の温度、\( T_e \) ：鍋の周りの空気の温度
この式の両辺について、\( T \) を \( t \) の関数として、\( \Delta t \to 0 \) の極限を取れば、次の微分方程式が得られます。
\[ k - a \left( T - T_{e} \right) = m C \frac{dT}{dt} \]
この微分方程式は変数分離法で解けます。
\[ \begin{align}
k - a \left( T - T_{e} \right) &= m C \frac{dT}{dt} \\\\
\frac{1}{mC} &= \frac{1}{k - a \left( T - T_{e} \right)} \cdot \frac{dT}{dt} \\\\
\int \frac{1}{mC} dt &= \int \frac{1}{k - a \left( T - T_{e} \right)} dT \\\\
\frac{t}{mC} + A &= - \frac{1}{a} \ln \left\{ k - a \left( T - T_{e} \right) \right\}
\end{align}\]
\( t = 0 \) のとき、\( T = T_0 \) とすると、
\[ A = - \frac{1}{a} \ln \left\{ k - a \left( T_0 - T_{e} \right) \right\} \]
よって、
\[ \begin{align}
\frac{t}{mC} - \frac{1}{a} \ln \left\{ k - a \left( T_0 - T_{e} \right) \right\} &= - \frac{1}{a} \ln \left\{ k - a \left( T - T_{e} \right) \right\} \\\\
- \frac{at}{mC} + \ln \left\{ k - a \left( T_0 - T_{e} \right) \right\} &= \ln \left\{ k - a \left( T - T_{e} \right) \right\} \\\\
\ln \frac{k - a \left( T_0 - T_{e} \right)}{k - a \left( T - T_{e} \right)} &= \frac{at}{mC} \\\\
\frac{k - a \left( T_0 - T_{e} \right)}{k - a \left( T - T_{e} \right)} &= e^{\frac{at}{mC}} \\\\
\frac{k - a \left( T - T_{e} \right)}{k - a \left( T_0 - T_{e} \right)} &= e^{-\frac{at}{mC}} \\\\
k - a \left( T - T_{e} \right) &= e^{-\frac{at}{mC}} \left\{ k - a \left( T_0 - T_{e} \right) \right\} \\\\
a \left( T - T_{e} \right) &= k - e^{-\frac{at}{mC}} \left\{ k - a \left( T_0 - T_{e} \right) \right\} \\\\
T - T_{e} &= \frac{k}{a} - \frac{1}{a} \cdot e^{-\frac{at}{mC}} \left\{ k - a \left( T_0 - T_{e} \right) \right\} \\\\
T &= T_e + \frac{k}{a} - e^{-\frac{at}{mC}} \left\{ \frac{k}{a} - \left( T_0 - T_{e} \right) \right\}
\end{align}\]
ナユミ
ごたついてるわね。
カヤ
まあ、パラメータが多いからな。けど、最後の式からもう少しこのモデルの意味を考えると、式をいい形に変形できる。
ナユミ
ほう、どういうこと？
カヤ
最後の式について、\( t \to \infty \) の極限を考えてみるんだ。
\[ \lim _{t \to \infty} T = T_e + \frac{k}{a} \]
\( e^{-\frac{at}{mC}} \) がかけられてる項は、\( t \to \infty \) で0になるため、その手前の二つの項だけが残ります。
この極限値を \( T_{max} \) として、\( a \) を \( T_{max} \) と他のパラメータで表してみます。
\[ \begin{align}
T_{max} &= T_e + \frac{k}{a} \\\\
\frac{k}{a} &= T_{max} - T_e \\\\
a &= \frac{k}{T_{max} - T_e}
\end{align}\]
これにより、\( a \) の代わりに \( T_{max} \) をモデルのパラメータとすることができます。
この式をさっきの \( T =\) の式に代入してみます。
\[ \begin{align}
T &= T_e + \frac{k}{a} - e^{-\frac{at}{mC}} \left\{ \frac{k}{a} - \left( T_0 - T_{e} \right) \right\} \\\\
&= T_e + \frac{k}{\frac{k}{T_{max} - T_e}} - e^{-\frac{\frac{k}{T_{max} - T_e}t}{mC}} \left\{ \frac{k}{\frac{k}{T_{max} - T_e}} - \left( T_0 - T_{e} \right) \right\} \\\\
&= T_e + T_{max} - T_e - e^{-\frac{kt}{mC \left( T_{max} - T_e \right) }} \left\{ T_{max} - T_e - \left( T_0 - T_{e} \right) \right\} \\\\
&= T_{max} - \left( T_{max} - T_0 \right) e^{-\frac{kt}{mC \left( T_{max} - T_e \right) }}
\end{align}\]
ナユミ
項が一つ減ってすっきりしたわね。それと、グラフの形がイメージしやすくなったわ。
カヤ
だな。じゃあ、この式を実際のデータに適用してみよう。
水の加熱実験
カヤ
今回は次のような実験をしてみたぞ。
１．鍋に480mlの水を入れた。
２．鍋にアルコール温度計を入れた。
３．コンロのスイッチを入れると同時にストップウォッチで計測を開始した。以後、30秒ごとに温度計を読み取り記録する作業を20分間継続した。コンロの火は弱火とした。
４．周りの空気の温度は、鍋の近くに置いた温度計の示した気温とし、実験開始時と終了時の気温の平均を取った。
２．鍋にアルコール温度計を入れた。
３．コンロのスイッチを入れると同時にストップウォッチで計測を開始した。以後、30秒ごとに温度計を読み取り記録する作業を20分間継続した。コンロの火は弱火とした。
４．周りの空気の温度は、鍋の近くに置いた温度計の示した気温とし、実験開始時と終了時の気温の平均を取った。
この実験のデータに対してモデルを適用するにあたって、水の比熱を決めなければなりませんが、水の比熱にはわずかに温度依存性があります。
水の比熱の温度依存性 \( C \) は次式で表されます。
\[ C = \left( -203.6060 + 1.523290T - 3.196413 \times 10^{-3} \times T^2 + 2.474455 \times 10^{-6} \times T^3 + \frac{3855326}{T^2} \right) \times \frac{1000}{18.02} \]
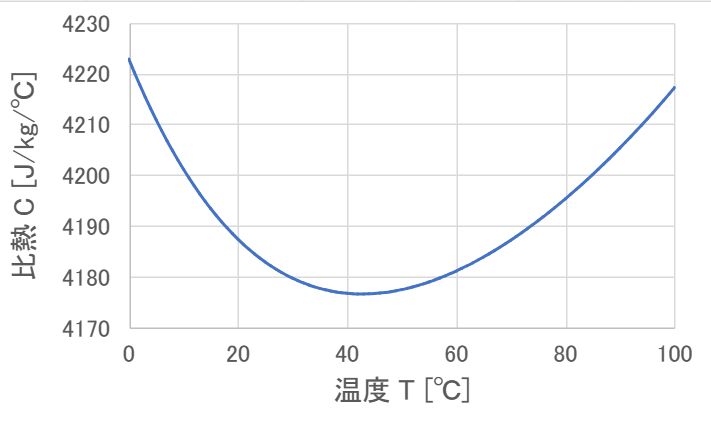
グラフを見ると0℃から100℃にかけて比熱の変化はあるものの、縦軸方向の動きは50程度しかなく、値は常に4000以上あることから、このぐらいの変化は無視しても構わないと考えられます。
そこで、比熱の値は0℃から100℃までの比熱の値を平均した値4191.1を使ってモデルを適用します。
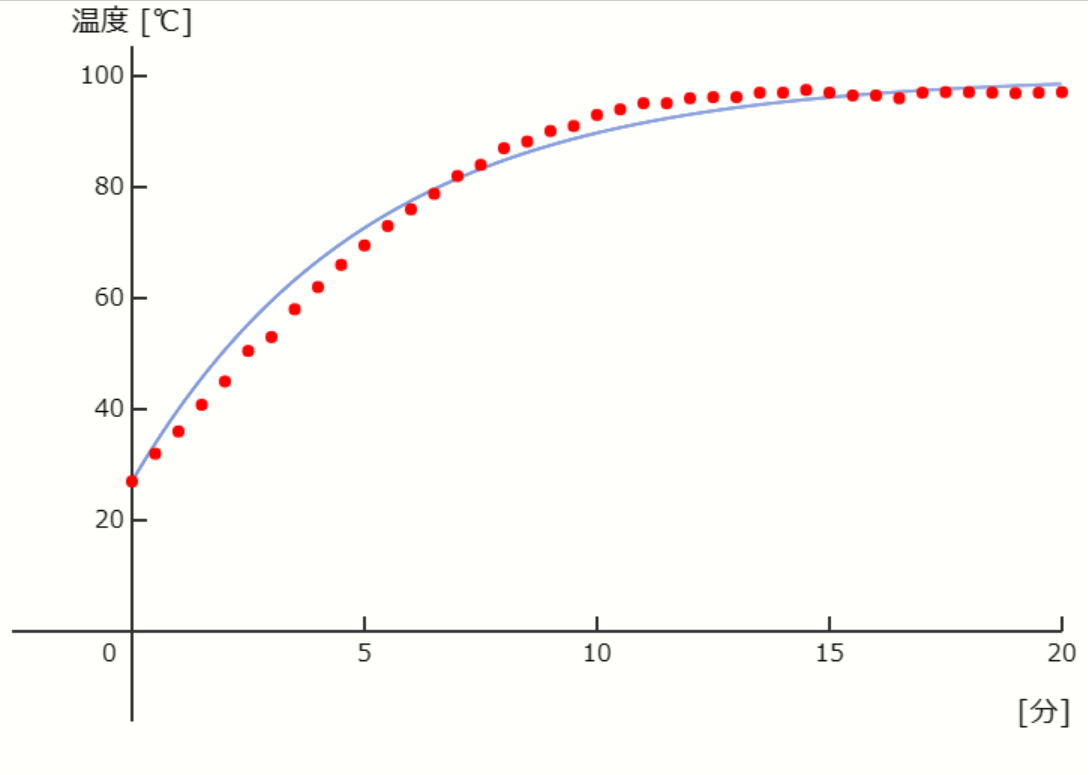
赤丸が実測値、青線がモデル式。
\( k = 480 \) 、\( T_0 = 27.0 \) 、\( T_e = 27.1 \) 、\( T_{max} = 100 \) 、\( m = 0.48 \) 、\( C = 4191.1 \)。
ナユミ
なかなかきれいに合ってるわね。
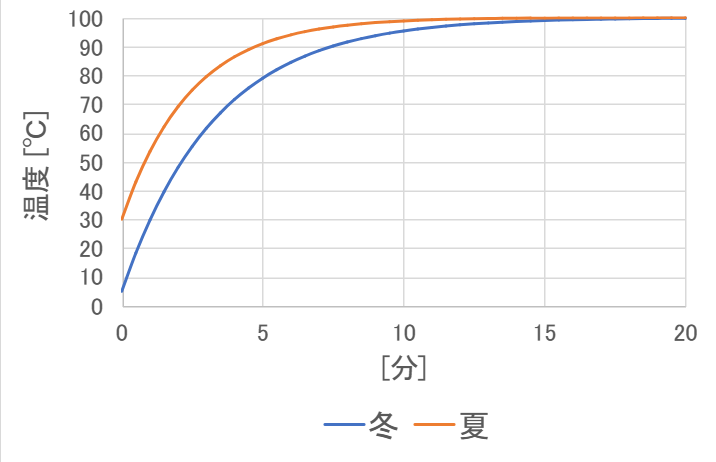
次に、ここで求めた \( k = 480 \) という値を使って、冬と夏の水の温まり方の違いについて考えてみます。冬は \( T_e = T_0 = 5 \) 、夏は \( T_e = T_0 = 30 \) としてグラフを書いてみます。
ナユミ
ふむふむ、90℃まで温まる時間を見ると、夏は9分ぐらいで、冬は15分ぐらいかな。ちょっとした用事が一つできるかどうかぐらいの差ね。
カヤ
そんなものだな。まあ、実際に湯を沸かすときは強火か中火くらいで沸かすだろうから、ここまでの時間差は出ないだろうけどな。
ナユミ
そうよね、そんなに時間差ないような気がするわ。それってこのモデルで表せたりする？
カヤ
そうだな、パラメータ \( k \) の大きさは火の強さを表しているから、これを倍の960にしてグラフを書いてみるとこうなる。
ナユミ
90℃になるまでの時間を見ると、夏は4分半、冬は7分半ぐらいね。ちょうどさっきの時間の半分くらいの時間でお湯が沸くのね。
カヤ
そんな感じだな。まあこうやって一度実験をしてパラメータを求めると、あとはそれをいろいろなパターンを想定しながら変化させて別の状況についてもすぐに考えることができるのが数値実験のいいところだな。
ナユミ
また実験するのも大変だもんね。
カヤ
そうなんだよな。
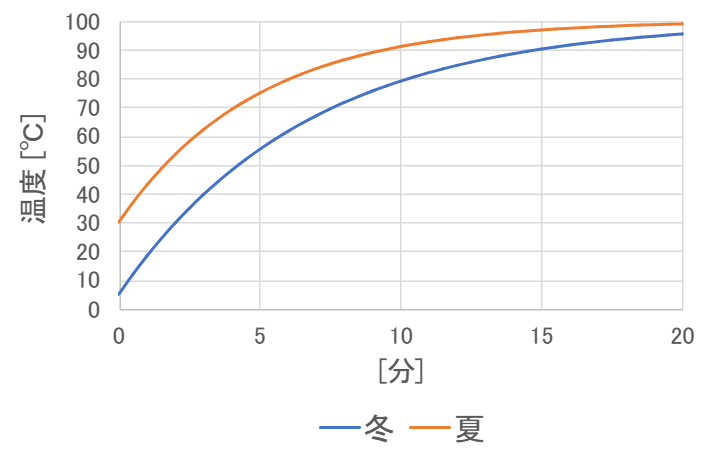
参考：
[1] WIKIBOOKS 中学校理科 第1分野/熱と温度、https://ja.wikibooks.org/wiki/中学校理科_第1分野/熱と温度、2023年9月6日閲覧
[2] 水の物性値、https://cattech-lab.com/science-tools/properties-water/、2023年9月7日閲覧
前の記事
第7話
フェルメールの贋作
～メーヘレンの事件～
フェルメールの贋作
～メーヘレンの事件～
次の記事
第9話
流行語～SIRモデル～
流行語～SIRモデル～