流行語～SIRモデル～

　　・SIRモデル

　　・流行語の検索数

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 5話、 6話、 7話、 8話、 9話

ナユミ

ねえ、カヤちゃん。この間久しぶりにテレビでIKKOさん見てね、「どんだけ～」って言いたくなったわ。

カヤ

「どんだけ～」な、よくIKKOさんが使ってるやつだな。

ナユミ

そうよ。私が小学校の時ぐらいにすごく流行ってね、クラスの友達もみんな何かにつけて「どんだけ～」って言ってふざけてたわ。

カヤ

そんなに流行ってたのか。カヤが小学校ぐらいのときは「半沢直樹」の「倍返しだ」が流行ってたぞ。対戦ゲームとかやって逆転するたびに「倍返しだ」って言って遊んでたな。

ナユミ

「倍返し」も流行ったわよね。もう今じゃあんまり見かけなくなったけどね。

カヤ

まあ、盛者必衰の理ってやつだな。

ナユミ

鎌倉時代から人は変わらないわね。こういう盛者必衰の理みたいなものを表す数理モデルっていうのもありそうね。

カヤ

それなら、コロナ絡みでニュースにもなったSIRモデルというものがあるぞ。

SIRモデル

　SIRモデルは感染症の短期的な流行を予測する基本的なモデルです。このモデルはスコットランドの生化学者 W.O.Kermack と、同じくスコットランドの疫学者 A.G.McKendrick との1927年の共著論文 "A Contribution to the Mathematical Theory of Epidemics" ではじめて紹介されました。 SIRモデルは次の3つの常微分方程式からなります。

\[ \rm SIR \ モデル\] 　閉ざされた集団の中に感染症が持ち込まれたケースを考える。ただし、感染後回復した患者は永続的な免疫を持ち、二度感染することはないとする。また、感染症の潜伏期間は非常に短いとする。このとき、集団を次の3つのグループに分ける。

[1] 感染症を人に移す可能性がある感染者 \( I \)
[2] 感染する可能性がある感染可能者 \( S \)
[3] 感染症により死亡したか、回復し免疫を獲得したか、隔離された除外者 \( R \)

これらの設定のもと、SIRモデルは次の3つの常微分方程式からなる。 \[ \begin{align} \frac{dS}{dt} &= - \beta SI \ldots (1) \\\\ \frac{dI}{dt} &= \beta SI - \gamma I \ldots (2) \\\\ \frac{dR}{dt} &= \gamma I \ldots (3) \end{align}\] ここで、\( \beta \) は感染率、\( \gamma \) は回復率（隔離率）であり、ともに正の定数である。

　3つの微分方程式を足し合わせると、次式が導かれます。

\[ \frac{dS}{dt} + \frac{dI}{dt} + \frac{dR}{dt} = 0 \]

　この式はこのままでは意味がわかりにくいので、次のように変形します。

\[ \begin{align} \frac{dS}{dt} + \frac{dI}{dt} + \frac{dR}{dt} &= 0 \\\\ \frac{d}{dt} \left( S + I + R \right) &= 0 \\\\ \int \frac{d}{dt} \left( S + I + R \right) dt &= \int 0 dt \\\\ S + I + R &= N \end{align}\] ここで、\( N \) は定数。

　S、I、Rの和は定数となり、これはこのモデルがちゃんと「閉ざされた集団」を表せていることの根拠になります。
　これらの微分方程式を近似などを用いずに \( S= \) といった形で解く方法は知られていません。そのため、最終的には数値解を求めることになりますが、その前に \[ \frac{dI}{dS}\] について考えてみます。

\[ \begin{align} \frac{dI}{dS} &= \frac{dI}{dt} \cdot \frac{dt}{dS} \end{align}\] ここで、\( t = f(S) \) とおき、この両辺を \( t \) で微分すると、 \[ \begin{align} t &= f(S) \\\\ 1 &= \frac{df(S)}{dt} = \frac{df(S)}{dS} \cdot \frac{dS}{dt} \\\\ \frac{1}{\frac{dS}{dt}} &= \frac{df(S)}{dS} = \frac{dt}{dS} \end{align}\] よって、 \[ \begin{align} \frac{dI}{dS} &= \frac{dI}{dt} \cdot \frac{dt}{dS} \\\\ &= \frac{dI}{dt} \cdot \frac{1}{\frac{dS}{dt}} \\\\ &= \left( \beta SI - \gamma I \right) \cdot \frac{1}{- \beta SI} \\\\ &= -1 + \frac{\gamma}{\beta} \cdot \frac{1}{S} \end{align}\]

　2-5行目から、\( \frac{dt}{dS} \) は \( \frac{dS}{dt} \) の逆数になることがわかります。これを、「逆関数の微分法」と呼ぶこともあります。
　最後の式を両辺 \( S \) で積分してみます。

\[ \begin{align} \frac{dI}{dS} &= -1 + \frac{\gamma}{\beta} \cdot \frac{1}{S} \\\\ \int \frac{dI}{dS} dS &= \int \left( -1 + \frac{\gamma}{\beta} \cdot \frac{1}{S} \right) dS \\\\ I &= -S + \frac{\gamma}{\beta} \ln S + C \end{align}\]

続いて、積分定数を求めて、特解を導きます。

\( t = 0 \) で、\( I = I_0 \) 、\( S = S_0 \) とすれば、 \[ \begin{align} I_0 &= -S_0 + \frac{\gamma}{\beta} \ln S_0 + C \\\\ C &= I_0 + S_0 - \frac{\gamma}{\beta} \ln S_0 \\\\ \end{align}\] 従って、 \[ \begin{align} I &= -S + \frac{\gamma}{\beta} \ln S + I_0 + S_0 - \frac{\gamma}{\beta} \ln S_0 \\\\ &= I_0 + S_0 -S + \frac{\gamma}{\beta} \ln \frac{S}{S_0} \end{align}\]

最後の式について、例として \( S_0 = 99 \) 、\( I_0 = 1 \) 、\( \beta = 0.003 \) 、\( \gamma = 0.1 \) として、横軸に \( S \) 、縦軸に \( I \) を書いたのが次のグラフになります。

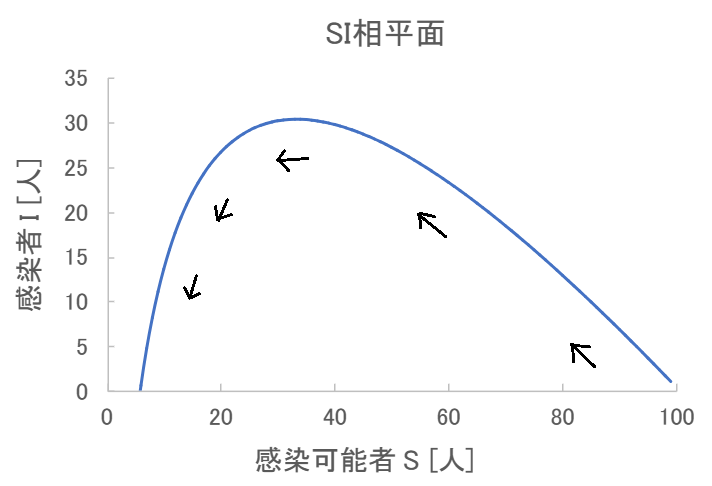
　時刻 \( t \) を変数とする関数の微分方程式が複数あるときに、それらの関数同士を組み合わせて \( xy \) 平面にプロットしたものを「軌道」と呼び、この場合の \( xy \) 平面を「相平面」と呼びます。上図は \( S(t) \) と \( I(t) \) の組み合わせでグラフを書いているため「SI相平面」と呼びます。グラフに書いてある矢印は時刻 \( t \) が進むにつれて、この軌道が進む方向を添え書きしたものです。初期値を \( S_0 = 99 \) 、\( I_0 = 1 \) としたため、軌道は右下から始まって左方向に進んでいきます。

　始めのうちは感染可能者 \( S \) が減るにつれ感染者 \( I \) はだんだん増えていきます。そのあと、あるところで感染者 \( I \) の数がピークに達し、その後は感染者 \( I \) は減少していきます。最終的には、感染者 \( I \) は0になり、感染可能者は一定数残ります。つまり、一定数は感染せずに済んだということになります。これを数式で表すなら、感染せずに済んだ人の数を \( S_{\infty} \) として、次のように表せます。

\[ \begin{align} & \lim _{t \to \infty } I = 0 \\\\ & \lim _{t \to \infty } S = S_{\infty} \end{align}\]

なお、この軌道は \( I = 0 \) できちんと止まりますが、それは次の極限からわかります。

\[ \begin{align} & \lim _{I \to 0} \frac{dS}{dt} = \lim _{I \to 0} \left( - \beta SI \right) = 0 \\\\ & \lim _{I \to 0} \frac{dI}{dt} = \lim _{I \to 0} \left( \beta SI - \gamma I \right) = 0 \end{align}\]

　\( \frac{dS}{dt} \) も \( \frac{dI}{dt} \) も \( I \) が0に近づくにつれてだんだん0に近づいていくので、 \[ \lim _{t \to \infty} (S,I) = \left( S_{\infty} , 0 \right) \] が成り立ちます。\( \left( S_{\infty} , 0 \right) \) を平衡点と呼びます。

　また、この軌道のピークの位置とピークの高さは次のように求めることができます。

\[ \begin{align} \frac{dI}{dS} &= -1 + \frac{\gamma}{\beta} \cdot \frac{1}{S} = 0 \\\\ 1 &= \frac{\gamma}{\beta} \cdot \frac{1}{S} \\\\ S &= \frac{\gamma}{\beta} \ \ (\rm ピークの位置) \end{align}\] これより、ピークの高さは、 \[ \begin{align} I &= I_0 + S_0 -S + \frac{\gamma}{\beta} \ln \frac{S}{S_0} \\\\ &= I_0 + S_0 - \frac{\gamma}{\beta} + \frac{\gamma}{\beta} \ln \frac{\frac{\gamma}{\beta}}{S_0} \\\\ &= I_0 + S_0 - \frac{\gamma}{\beta} \left( 1 - \ln \frac{\gamma}{\beta S_0} \right) \end{align}\]

　回復率 \( \gamma \) を感染率 \( \beta \) で割ったものがSI相平面のピーク位置になります。このピークの位置を閾値、またはしきい値と呼びます。この呼び名は、\( \frac{dI}{dS} \) の正負が閾値を境に切り替わるため、感染拡大は \( S_0 \) が閾値より大きいときに限って起こることに由来します。

ナユミ

どんな感染も必ず閾値を迎えて、その後は消えてゆく。SIRモデルでは盛者必衰の理がここに現れているのね。

カヤ

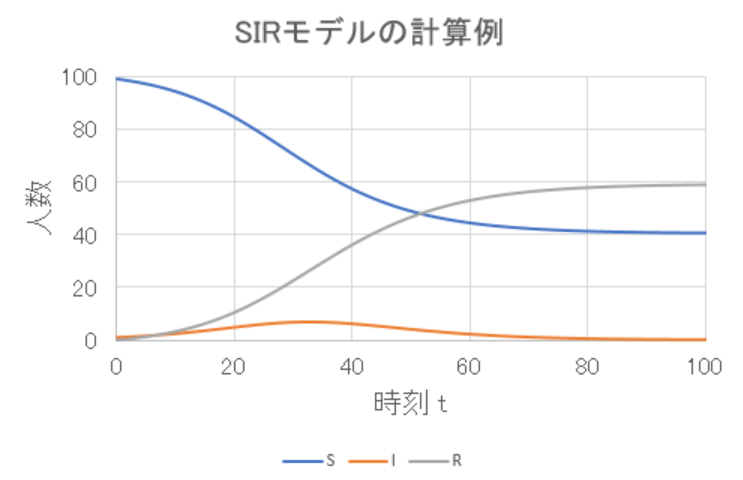
そういうことだな。それじゃあ、具体的なSIRモデルの計算例を見てみよう。

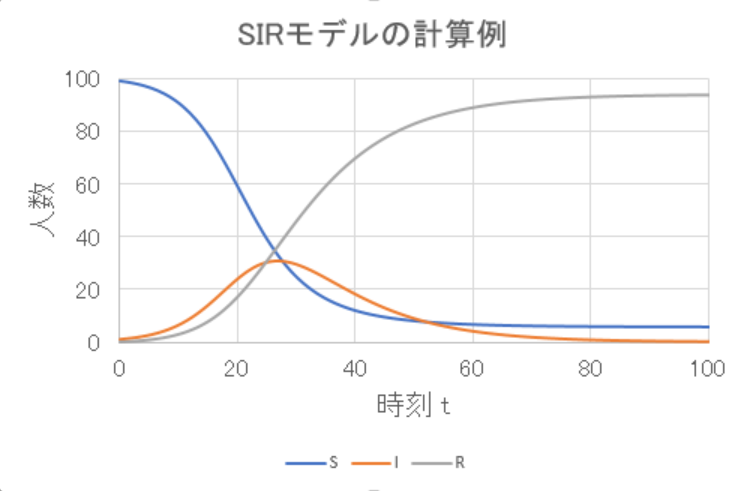
\( \beta = 0.003 \) 、\( \gamma = 0.1 \) 、\( S_0 = 99 \) 、\( I_0 = 1 \) 、\( R_0 = 0 \) としてオイラー法により計算。

　青線の感染可能者 \( S \) が減るにつれて橙色の感染者 \( I \) と灰色の除外者 \( R \) が増えてきます。感染者は峠を越えたら減ってゆき、最終的にいなくなります。最後に残るのは感染せずに済んだ \( S_{\infty} \) と除外者 \( R \) だけになります。
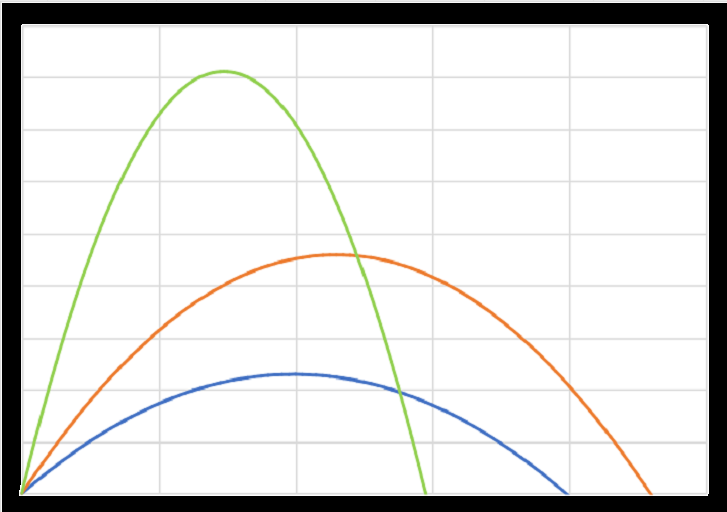
　感染者のピークの高さはさっき導出した式から、 \[ \begin{align} I &= 1 + 99 - \frac{0.1}{0.003} \left( 1 - \ln \frac{0.1}{0.003 \times 99} \right) \\\\ &= 30.38 \ldots \end{align}\] となり、グラフとも合致していることがわかります。比較として、\( \beta = 0.006 \) にしたものと、\( \gamma = 0.2 \) にしたものを見てみます。

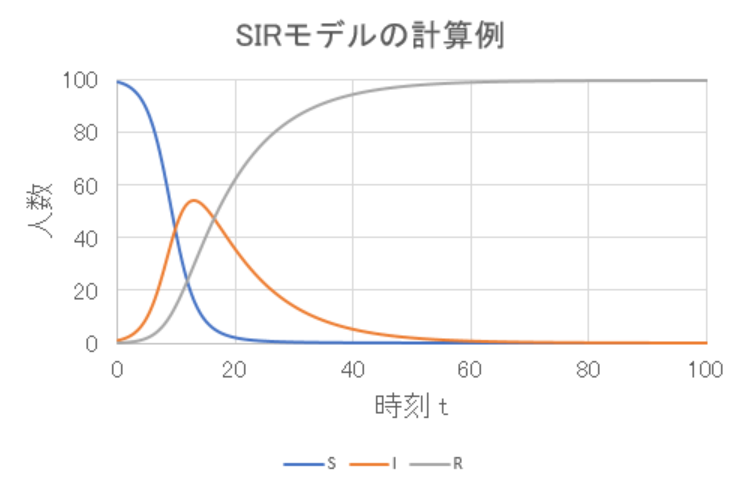
\( \beta = 0.006 \) 、\( \gamma = 0.1 \) 、\( S_0 = 99 \) 、\( I_0 = 1 \) 、\( R_0 = 0 \) としてオイラー法により計算。

\( \beta = 0.003 \) 、\( \gamma = 0.2 \) 、\( S_0 = 99 \) 、\( I_0 = 1 \) 、\( R_0 = 0 \) としてオイラー法により計算。

　\( \beta = 0.006 \) としたものは感染者 \( I \) のピークが高くなり、グラフが全体的に横に圧縮されたようになっています。また、感染せずに済んだ人が減っています。
　一方、\( \gamma = 0.2 \) としたものは感染者 \( I \) のピークが低くなり、グラフが全体的に横に引き延ばされたようになっています。そして、感染せずに済んだ人は増えています。

ナユミ

SIRモデルのパラメータの効果が少しわかってきたわ。

カヤ

それじゃあ、このモデルを流行語の検索数に当てはめてみよう。

流行語の検索数

　流行語の検索数について調べるために、「Google トレンド」というサービスを使いました。このサイトでは、指定した言葉のGoogle検索での検索数の経時変化を0から100の相対値で調べることができます。このサイトだけでは正確な検索数は調べられませんが、検索数の推移を調べるには有用なツールです。

ナユミ

へえ、便利なサイトがあるのね。それで、検索数をSIRモデルで表すというのは？

カヤ

これは、次のような対応を仮定してみたらいい。

「ウイルス」→「言葉」、「感染者」→「言葉を検索した人」
「言葉を検索した人」の数は「検索数の相対値」に比例する。

　この仮定は、「言葉を検索した人は言葉の力によって検索してしまった」という考えに基づいています。また、「感染者」→「言葉を検索した人」という対応は、「言葉を検索する」という行動が「言葉の感染拡大の原因になる」ことを仮定しています。
　検索すること自体が周りの人に影響を与えるという考えは少しわかりにくいですが、次の2つの仮定に基づいています。

[1] 言葉を検索する人はその言葉に興味を持っていると考えられる。そして、匿名掲示板やSNS等、個人が気軽に言葉を発信できる場所は山ほどある。そのため、その人が何らかの形でその言葉を発信する可能性は高い。
[2] マスコミ等も検索数の推移やSNSでの盛り上がり具合等を見ながら番組や記事の内容を構成していると思われる。

　こういった文脈のもと「検索数の相対値」が「言葉の感染者」の数を反映していると見ることは、そこまでおかしな話ではないと思われます。

ナユミ

そういうことね。「感染者」が「検索数の相対値」に比例するという考えの背景がよくわかったわ。

カヤ

じゃあ、実際にSIRモデルを適用した例を見てみよう。選んだ言葉は冒頭に話していた「どんだけ～」と「倍返し」、それと「3つの密」だな。それぞれ流行し始めたあたりから1年間の検索数の相対値に対してSIRモデルのIを当てはめてみたぞ。

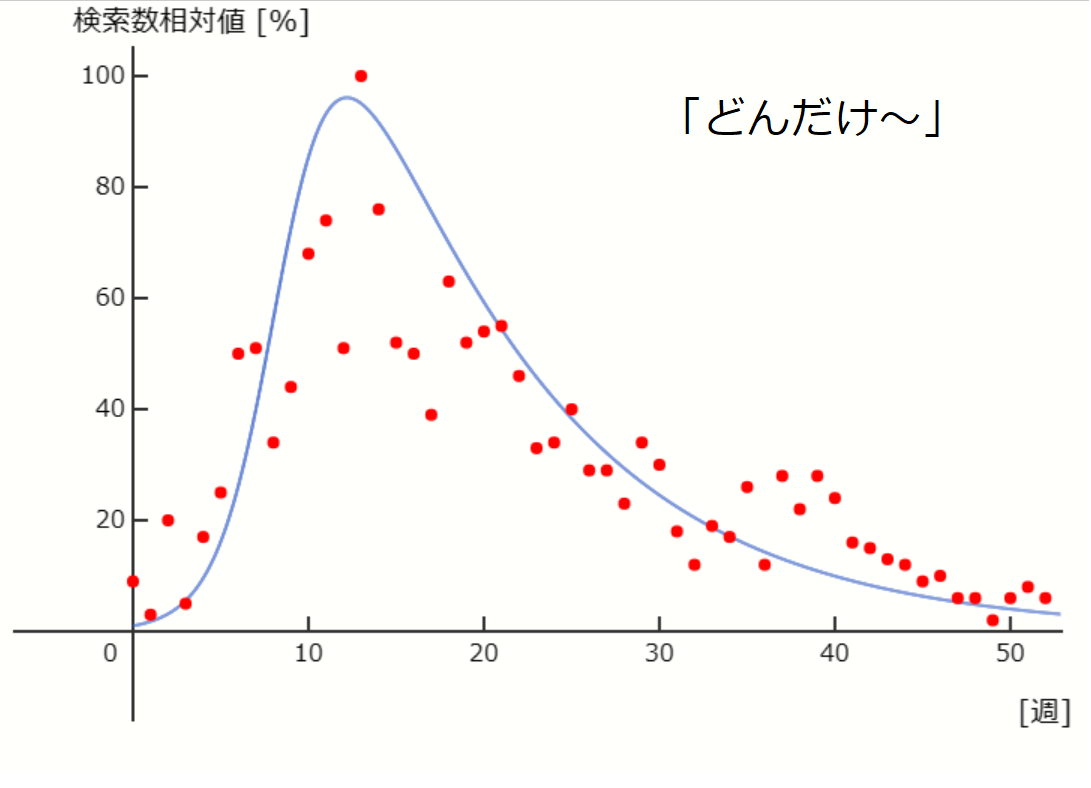
赤丸が実測値、青線がSIRモデル。
\( \beta = 0.0006 \) 、\( \gamma = 0.013 \) 、\( S_0 = 160 \) 、\( I_0 = 1 \) 、\( R_0 = 0 \) としてオイラー法により計算。
実測値は2007/3/18-2008/3/16までの1週間毎のGoogle トレンドのデータを使用。

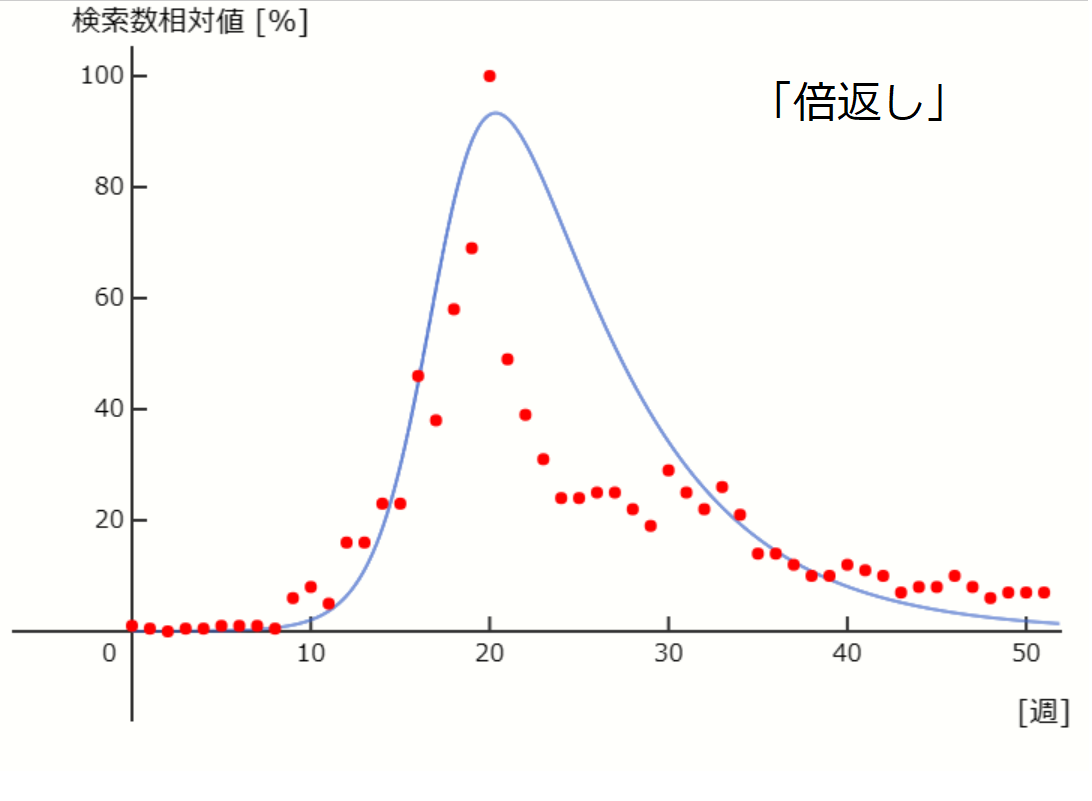
赤丸が実測値、青線がSIRモデル。
\( \beta = 0.00053 \) 、\( \gamma = 0.022 \) 、\( S_0 = 200 \) 、\( I_0 = 0.006 \) 、\( R_0 = 0 \) としてオイラー法により計算。
実測値は2013/5/5-2014/4/27までの1週間毎のGoogle トレンドのデータを使用。

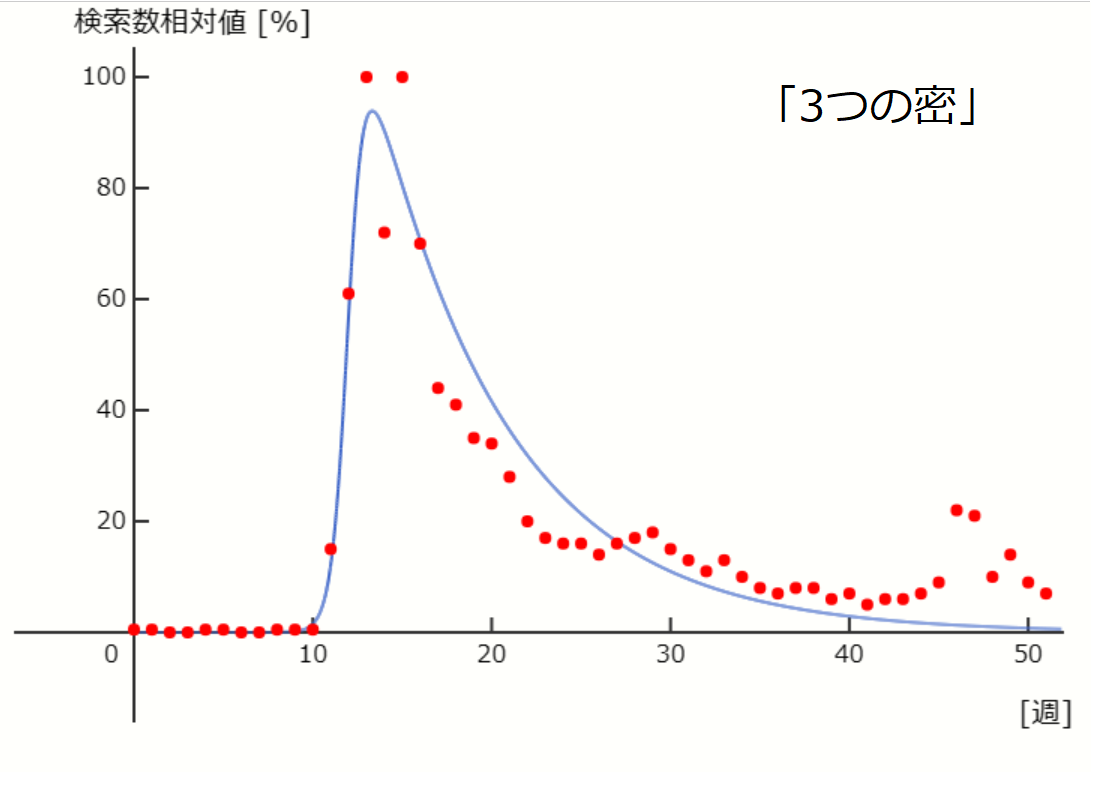
赤丸が実測値、青線がSIRモデル。
\( \beta = 0.0028 \) 、\( \gamma = 0.019 \) 、\( S_0 = 120 \) 、\( I_0 = 5 \times 10^{-10} \) 、\( R_0 = 0 \) としてオイラー法により計算。
実測値は2020/1/5-2020/12/27までの1週間毎のGoogle トレンドのデータを使用。

ナユミ

うーん、ところどころ合ってないところもあるけど、大まかな傾向は捉えられている感じがするわね。

カヤ

そうだな。「倍返し」の21-24週の急激な低下、その後の20%程度での推移は表すのが難しかったな。それと、「3つの密」の46週目にある2個めのピークは、感染者のピークは1つだけというモデルの性質上表すことができなかった。

ナユミ

けど、言葉の流行が感染症の流行と似たような動きをするっていうのを知れただけでもよかったわ。

カヤ

それならよかったぞ。あと、どんな言葉でもSIRモデルでその流行を表せるわけじゃない。いい例が「天気」だな。

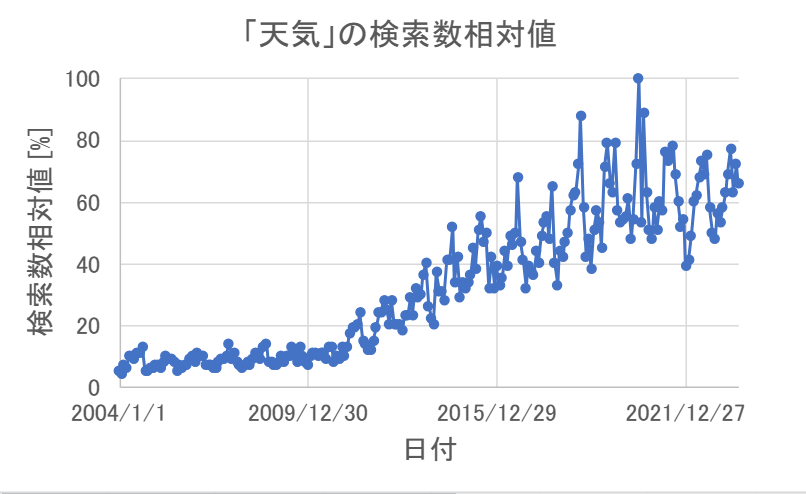
2004/1/1-2023/9/1までの1ヶ月毎のGoogle トレンドのデータを使用。

　「天気」のように日常的に検索することが当たり前の言葉は短期的な流行を表すSIRモデルでは表すことが難しいです。これはSIRモデルが季節性インフルエンザのように一定の割合で発生し続けるエンデミックの表現が難しいと言われていることに対応していると考えられます。
　一方、検索数の相対値が右上がりに増えていることから、「天気」を検索する人は年々増えてきていることがわかります。これは、「天気」に関心を持つ人が年々増えているというよりも、「天気」に限らずGoogle検索をする人が増えてきているということだと思われます。

ナユミ

そういうことね。みんなだんだんGoogle検索が当たり前になってきてるのね。

カヤ

そういうことだな。結局、一番流行しているのは「Google検索をする」という行動かもしれないな。

ナユミ

じゃあ、私も「Google検索」の感染者として、今からお夕飯のレシピを検索するわ。

カヤ

よろしく、感染者さん♪

参考：
[1] Wikipedia 新語・流行語大賞、https://ja.wikipedia.org/wiki/新語・流行語大賞、2023年9月8日閲覧
[2] Google トレンド、https://trends.google.co.jp/trends/、2023年9月8日閲覧
[3] David Burghes／Morag Borrie　著、垣田高夫／大町久佐栄　訳、微分方程式で数学モデルを作ろう、日本評論社、1990年4月28日発行
[4] Wikipedia SIRモデル、https://ja.wikipedia.org/wiki/SIRモデル、2023年9月9日閲覧
[5] W.O.Kermack and A.G.McKendrick、A Contribution to the Mathematical Theory of Epidemics、1927年
[6] George Allen & Unwin Ltd 著、矢野健太郎　訳補、ブルーバックス　現代数学百科、講談社、1968年11月30日発行

第8話
水が沸騰するまでの
温度変化

第10話
斜方投射の運動方程式