目次
・ニュートンの運動方程式
・万有引力
・力と速度の分解
・斜方投射
・斜方投射の実験
ナユミ
カヤちゃん、昨日探偵ガリレオシリーズを見返しててね、映画二作目の「真夏の方程式」の最後にこんな数式が出てたんだけど…。
\[ L = \frac{v^2 \sin 2 \theta }{g} \]
カヤ
これな。斜方投射の水平方向の移動距離を表す式だな。
ナユミ
斜方投射？ってあのペットボトルロケットの動きのこと？
カヤ
そうだぞ。あのロケットの発射台からロケットの落下地点までの水平方向の距離がこの式で表されるんだ。
ナユミ
へえ、そうなんだ。この式って私でも導けたりするのかしら？映画では恭平君のお父さんが首を傾げてたけど。
カヤ
この式は高校物理で出てくる式だし、ナユ姉もちょっとやればできると思うぞ。
ナユミ
本当？ちょっと教えてほしいわ。
カヤ
じゃあまずは、ニュートンの運動方程式から説明しようか。
ニュートンの運動方程式
ニュートンの運動方程式はニュートンが1687年に著した「プリンキピア」という書物に端を発した古典力学の基礎となる微分方程式です。
ニュートンの運動方程式は「プリンキピア」においては微分方程式の形式では書かれていませんでしたが、ニュートン以後、オイラーなど18世紀の多くの科学者によって現在の形式に整えられました。
ニュートンの運動方程式は物体に働く「力」と、物体の「質量」と「速度」を次の関係式で結びつけます。
ニュートンの運動方程式は物体に働く「力」と、物体の「質量」と「速度」を次の関係式で結びつけます。
\[ ニュートンの運動方程式 \ ( 運動の第二法則 ) \]
\[ F = \frac{d}{dt} \left( mv \right) \]
\( F \) ：物体に働く力、\( m \) ：物体の質量 (正の実数)、\( v \) ：物体の速度、\( t \) ：時刻
また、ニュートンの運動方程式の力を \( F = 0 \) とし、質量 \( m \) を時刻によらない定数としたものは運動の第一法則と呼ばれています。
\[ 運動の第一法則 \]
ニュートンの運動方程式において、\( F = 0 \) 、\( m \gt 0 \) を定数とすると、
\[ 0 = m \frac{dv}{dt} \]
よって、
\[ \frac{dv}{dt} = 0\]
運動の第一法則は「物体に外から力が働かなければ、その物体は静止し続けるか、等速直線運動を続ける」と読むことができ、これは慣性の法則とも呼ばれています。
ナユミ
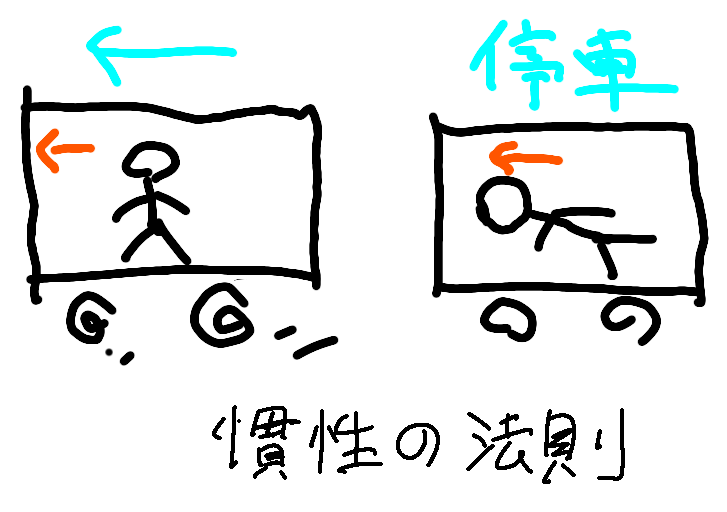
慣性の法則なら聞いたことあるわ。電車のつり革につかまってる時に急停車するとぐわんってなるあれよね。
カヤ
ああ、それだな。あれは電車が急停止した時、電車の中に立っている人は等速直線運動を続けようとするから、身体が電車の進行方向に向かって倒れてしまうんだな。
ナユミ
ニュートンの運動方程式では、力が運動の様子を決めているのね。ところで、力ってどういうもの？
カヤ
いろいろな力があるが、斜方投射を考える上で大事なのは万有引力だな。
万有引力
万有引力はあらゆる物体同士の間に働く引力のことで、二つの物体の質量の積を物体間の距離の2乗で割ったものに比例します。
\[ 万有引力 \]
\[ F = G \frac{m_1 m_2}{r^2} \]
\( G \) ：万有引力定数、\( m_1 \) ：物体1の質量、\( m_2 \) ：物体2の質量、\( r \) ：物体1と物体2の間の距離
万有引力はあらゆる物体の間に働きますが、普通はいろいろな方向に働く万有引力が打ち消しあうため、物体がどこかに引っ張られるということはありません。
ただし、万有引力が二物体の質量の積に比例する以上、地表面付近の運動を考える場合「地球」という巨大な質量だけは無視することができません。
そこで、万有引力の式を次のように変形および近似して使うことが多いです。
\( m_2 \) を地球の質量とし、\( r \) を地球の半径とすると、
\[ F = G \frac{m_1 m_2}{r^2} = m_1 g_e \]
\( g_e \) ：重力加速度に寄与する地球から受ける万有引力の影響
重力加速度は地表面付近で物体を自由落下させたときの、その物体の加速度のことです。
自由落下とは、空気抵抗を無視した空間において、物体を初速0で落下させることです。
加速度は速度の時間変化のことです。「速度」の速度と言っても構いません。
加速度を \( a \) として式で書くと次式になります。
\[ a = \frac{dv}{dt} \]
なお、速度は英語でvelocity、加速度はaccelerationと呼ぶため、速度は \( v \) 、加速度は \( a \) で表すことが多いです。
また、重力加速度はほとんど万有引力で決まりますが、これに少しだけ地球の自転による遠心力の効果が加わっているため、重力加速度 \( g \) は次式で表されます。
また、重力加速度はほとんど万有引力で決まりますが、これに少しだけ地球の自転による遠心力の効果が加わっているため、重力加速度 \( g \) は次式で表されます。
\[ g = g_e + g_c \]
\( g \) ：重力加速度、\( g_e \) ：地球から受ける万有引力の影響、\( g_c \) ：地球の自転による遠心力の影響
ナユミ
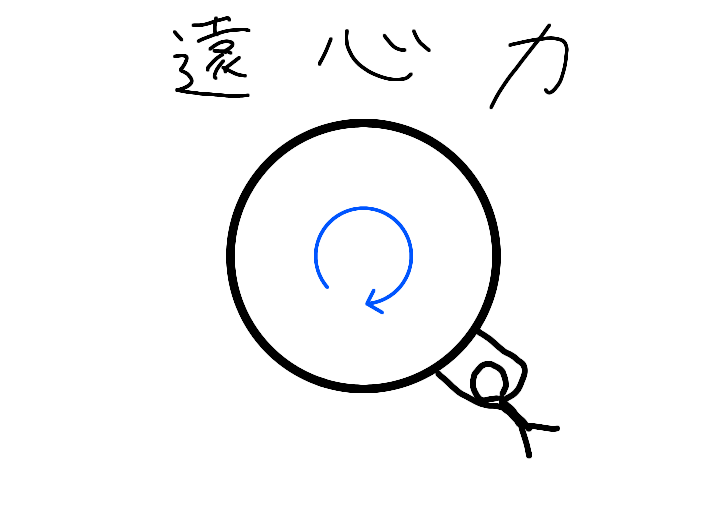
遠心力ってタオルをぶんぶん振り回してるときに引っ張られるアレ？
カヤ
まああれだな。イメージ的にはそのタオルの先を地表面として、そこにしがみついているのが地表面付近にある物体ということになる。
ナユミ
私はそんな頑張って地球にしがみついてる気しないけどね。
カヤ
それは地球の自転による遠心力よりも万有引力のほうがずいぶんと大きいからな。
地球の自転による遠心力の影響は緯度により異なります。
そのため、重力加速度の大きさも緯度によってわずかに異なりますが、
およその値は \( 9.8 \rm \left[ m / s^2 \right] \) です。
ナユミ
地球が私を引っ張って放さないのね。
カヤ
そういうことだな。
ナユミ
ところで、そろそろ映画の式に手がつけられるかしら？
カヤ
じれったいようだが、あと一つ、力と速度の分解についてだけ説明しておきたい。
力と速度の分解
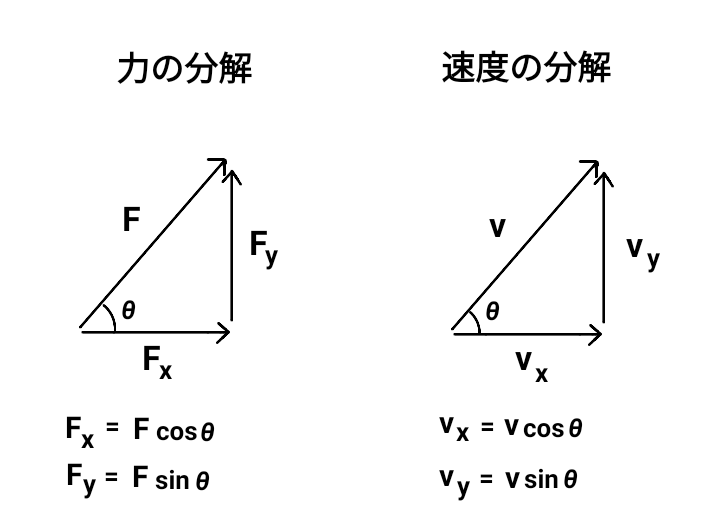
力も速度も横方向と縦方向に分解します。
分解に \( \sin \) と \( \cos \) が出てくるのは、単位円の半径を \( F \) 倍、あるいは \( v \) 倍したと考えます。
力や速度を二方向に分解することで、それぞれの方向についてニュートンの運動方程式を立てることができます。
カヤ
じゃあ、おまちかねの斜方投射の問題に入っていこう。
斜方投射
\( t = 0 \) において、原点から角度 \( \theta \) 、初速 \( v_0 \) で質量 \( m \) のロケットが発射されたとします。
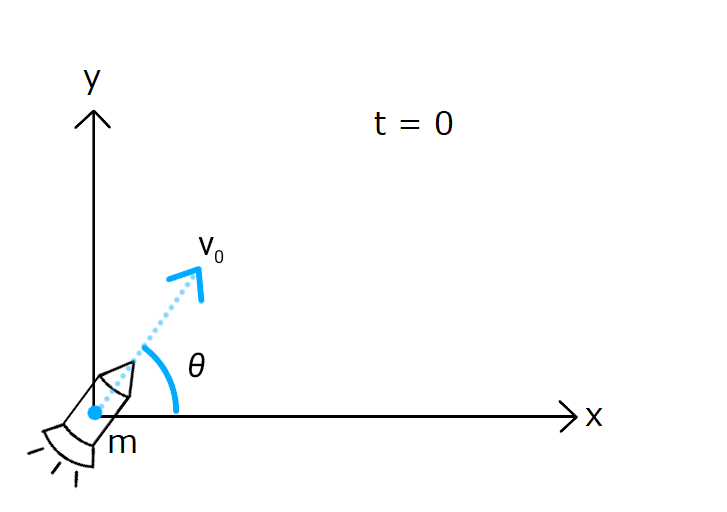
運動方程式は \( x \) 軸方向と \( y \) 軸方向に分けて次のように書くことができます。
\( x \) 軸方向
\[ 0 = \frac{d}{dt} \left( m v_x \right) \]
\( y \) 軸方向
\[ -mg = \frac{d}{dt} \left( m v_y \right) \]
重力加速度の影響があるのは \( y \) 軸方向だけなので、\( x \) 軸方向には力は働いていません。
また、\( y \) 軸方向の力は下向きに働いているため、運動方程式の左辺にはマイナスの符号がついています。
それから、質量 \( m \) についてですが、映画の実験の様子を真面目に考えると、ペットボトルロケットから水が射出されて空に飛びあがるので、質量は時刻の変化に伴い変化することになります。 ですが、今回は単純化のためと冒頭の数式を導くために、この質量は定数とします。 すると、先ほどの二つの運動方程式は次のようになります。
それから、質量 \( m \) についてですが、映画の実験の様子を真面目に考えると、ペットボトルロケットから水が射出されて空に飛びあがるので、質量は時刻の変化に伴い変化することになります。 ですが、今回は単純化のためと冒頭の数式を導くために、この質量は定数とします。 すると、先ほどの二つの運動方程式は次のようになります。
\( x \) 軸方向
\[ \begin{align}
0 &= m \frac{dv_x}{dt} \\\\
0 &= \frac{dv_x}{dt}
\end{align}\]
\( y \) 軸方向
\[ \begin{align}
-mg &= m \frac{dv_y}{dt} \\\\
-g &= \frac{dv_y}{dt}
\end{align}\]
\( x \) 軸方向も \( y \) 軸方向も質量 \( m \) は運動に関係していないことがわかります。
とはいえ、これはロケットの初速を \( v_0 \) で与えるため、モデルの上では気にならないだけです。
実際の実験でこの初速 \( v_0 \) を大きくするためには、軽いロケットの素材と、強い勢いでの水の射出が必要です。 映画ではガリレオ先生が自転車の空気入れでロケットに空気を入れていたので、 より現実に似せたモデルを作るなら、初速はロケット内の空気圧とロケット内の水を含んだ重さの関数として与えるべきだと思います。
ただ、映画ではロケットに釣り糸を付けて、カウンターリールの表示で飛距離を測定していました。 映画の式を使えば、初速はこの飛距離から計算で求められるので、今回はこのモデルで十分なのだと思います。
運動方程式を \( v_x \) 、\( v_y \) について解いていきます。
実際の実験でこの初速 \( v_0 \) を大きくするためには、軽いロケットの素材と、強い勢いでの水の射出が必要です。 映画ではガリレオ先生が自転車の空気入れでロケットに空気を入れていたので、 より現実に似せたモデルを作るなら、初速はロケット内の空気圧とロケット内の水を含んだ重さの関数として与えるべきだと思います。
ただ、映画ではロケットに釣り糸を付けて、カウンターリールの表示で飛距離を測定していました。 映画の式を使えば、初速はこの飛距離から計算で求められるので、今回はこのモデルで十分なのだと思います。
運動方程式を \( v_x \) 、\( v_y \) について解いていきます。
\( x \) 軸方向
\[ \begin{align}
0 &= \frac{dv_x}{dt} \\\\
\int 0 dt &= \int \frac{dv_x}{dt} dt \\\\
C &= v_x
\end{align}\]
\( t = 0 \) のとき、\( v_{x} = v_0 \cos \theta \) より、\( C = v_0 \cos \theta \) 。
よって、
\[ v_x = v_0 \cos \theta \]
\( y \) 軸方向 \[ \begin{align} -g &= \frac{dv_y}{dt} \\\\ \int -g dt &= \int \frac{dv_y}{dt} dt \\\\ -gt + D &= v_y \end{align}\] \( t = 0 \) のとき、\( v_{y} = v_0 \sin \theta \) より、\( D = v_0 \sin \theta \) 。 よって、 \[ v_y = -gt + v_0 \sin \theta \]
\( y \) 軸方向 \[ \begin{align} -g &= \frac{dv_y}{dt} \\\\ \int -g dt &= \int \frac{dv_y}{dt} dt \\\\ -gt + D &= v_y \end{align}\] \( t = 0 \) のとき、\( v_{y} = v_0 \sin \theta \) より、\( D = v_0 \sin \theta \) 。 よって、 \[ v_y = -gt + v_0 \sin \theta \]
\( v_x \) と \( v_y \) が求まったので、次はこれらから時刻 \( t \) におけるロケットの位置 \( (x(t),y(t)) \) を求めます。
\( x \) 軸方向
\[ v_x = \frac{dx}{dt} \]
であるから、
\[ \begin{align}
\frac{dx}{dt} &= v_0 \cos \theta \\\\
\int \frac{dx}{dt} dt &= \int \left( v_0 \cos \theta \right) dt \\\\
x &= \left( v_0 \cos \theta \right) t + C
\end{align}\]
\( t = 0 \) のとき、\( x = 0 \) より、\( C = 0 \) 。
よって、
\[ x = \left( v_0 \cos \theta \right) t \]
\( y \) 軸方向 \[ v_y = \frac{dy}{dt} \] であるから、 \[ \begin{align} \frac{dy}{dt} &= -gt + v_0 \sin \theta \\\\ \int \frac{dy}{dt} dt &= \int \left( -gt + v_0 \sin \theta \right) dt \\\\ y &= - \frac{1}{2} gt^2 + \left( v_0 \sin \theta \right) t + D \end{align}\] \( t = 0 \) のとき、\( y = 0 \) より、\( D = 0 \) 。 よって、 \[ y = - \frac{1}{2} gt^2 + \left( v_0 \sin \theta \right) t \]
\( y \) 軸方向 \[ v_y = \frac{dy}{dt} \] であるから、 \[ \begin{align} \frac{dy}{dt} &= -gt + v_0 \sin \theta \\\\ \int \frac{dy}{dt} dt &= \int \left( -gt + v_0 \sin \theta \right) dt \\\\ y &= - \frac{1}{2} gt^2 + \left( v_0 \sin \theta \right) t + D \end{align}\] \( t = 0 \) のとき、\( y = 0 \) より、\( D = 0 \) 。 よって、 \[ y = - \frac{1}{2} gt^2 + \left( v_0 \sin \theta \right) t \]
1 行目に書いてありますが、速度は位置を時刻で微分したものです。
今までの微分方程式による数理モデル同様、時間とともに変化する量を時刻で微分すれば、その量の変化速度になるという関係は運動方程式でも変わりません。
上で求めた \( x \) と \( y \) の式から、\( y \) を \( x \) の式で表すと次のようになります。
上で求めた \( x \) と \( y \) の式から、\( y \) を \( x \) の式で表すと次のようになります。
\[ x = \left( v_0 \cos \theta \right) t \]
より、
\[ t = \frac{x}{v_0 \cos \theta} \]
これを、
\[ y = - \frac{1}{2} gt^2 + \left( v_0 \sin \theta \right) t \]
に代入すると、
\[ \begin{align}
y &= - \frac{1}{2} g \left( \frac{x}{v_0 \cos \theta} \right)^2 + \left( v_0 \sin \theta \right) \cdot \frac{x}{v_0 \cos \theta} \\\\
&= - \frac{g}{2{v_0}^2 \cos ^2 \theta} x^2 + \frac{\sin \theta}{\cos \theta} x \\\\
&= - \frac{g}{2{v_0}^2 \cos ^2 \theta} x^2 + \left( \tan \theta \right) x
\end{align}\]
例として、\( g = 9.8 \rm \left[ m/s^2 \right] \) 、\( v_0 = 30 \rm \left[ m/s \right] \) 、 \( \theta = \frac{\pi}{4} \) としてグラフを書くと下図のようになります。
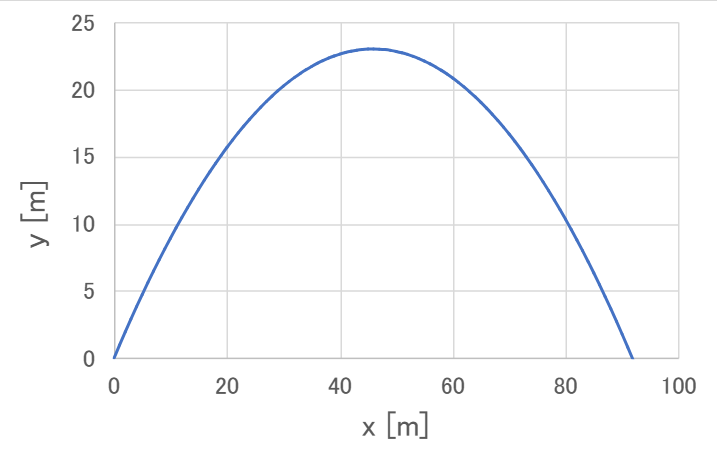
頂点が原点にないですが、これも放物線のグラフです。
「放物線」という言葉の由来は、この斜方投射の運動方程式の解から来ているのだと思います。
このグラフの頂点の位置は頂点で \( y \) 軸方向の速度 \( v_y \) が0であるという性質を使って求められます。
まずは、頂点の \( x \) 座標を求めてみます。
\[ v_y = -gt + v_0 \sin \theta \]
頂点では、\( v_y = 0 \) なので、
\[ \begin{align}
0 &= -gt + v_0 \sin \theta \\\\
t &= \frac{v_0 \sin \theta}{g}
\end{align}\]
これを、
\[ x = \left( v_0 \cos \theta \right) t \]
に代入すると、頂点の \( x \) 座標は、
\[ \begin{align}
x &= \left( v_0 \cos \theta \right) \cdot \frac{v_0 \sin \theta}{g} \\\\
&= \frac{{v_0}^2 \cos \theta \sin \theta}{g}
\end{align}\]
ここで、三角関数の積を和に直す公式より、
\[ \begin{align}
\cos \theta \sin \theta &= \frac{1}{2} \left\{ \sin \left( \theta + \theta \right) - \sin \left( \theta - \theta \right) \right\} \\\\
&= \frac{1}{2} \left\{ \sin 2 \theta - \sin 0 \right\} \\\\
&= \frac{\sin 2 \theta}{2}
\end{align}\]
よって、
\[ x = \frac{{v_0}^2 \sin 2 \theta}{2g} \]
続いて、頂点の \( y \) 座標を求めます。
ロケットが頂点に達する時刻
\[ t = \frac{v_0 \sin \theta}{g} \]
これを、
\[ y = - \frac{1}{2} gt^2 + \left( v_0 \sin \theta \right) t \]
に代入すると、
\[ \begin{align}
y &= - \frac{1}{2} g \left( \frac{v_0 \sin \theta}{g} \right)^2 + \left( v_0 \sin \theta \right) \cdot \frac{v_0 \sin \theta}{g} \\\\
&= - \frac{{v_0}^2 \sin ^2 \theta}{2g} + \frac{{v_0}^2 \sin ^2 \theta}{g} \\\\
&= \frac{{v_0}^2 \sin ^2 \theta}{2g}
\end{align}\]
ナユミ
だいぶと斜方投射についてわかって気がするけど、映画の最後の式はどうやって求めるのかな？
カヤ
実はもうほとんど答えは出ているぞ。
放物線は頂点を通る軸を中心に線対称なので、先ほど求めた頂点の位置の \( x \) 座標を2倍したものがロケットの着水点の \( x \) 座標、つまりロケットの飛距離を表す映画の最後の式になります。
\[ \begin{align}
L &= 2 \cdot \frac{{v_0}^2 \sin 2 \theta}{2g} = \frac{{v_0}^2 \sin 2 \theta}{g}
\end{align}\]
ナユミ
そういうことね。でも、映画の式は \( v_0 \) じゃなくて \( v \) だったけど…
カヤ
それは、単に映画の式は初速を \( v \) と置いてるだけだ。
ナユミ
それだけなのね。じゃあ、結構長かったけど、これで映画の式が求められたのね。
カヤ
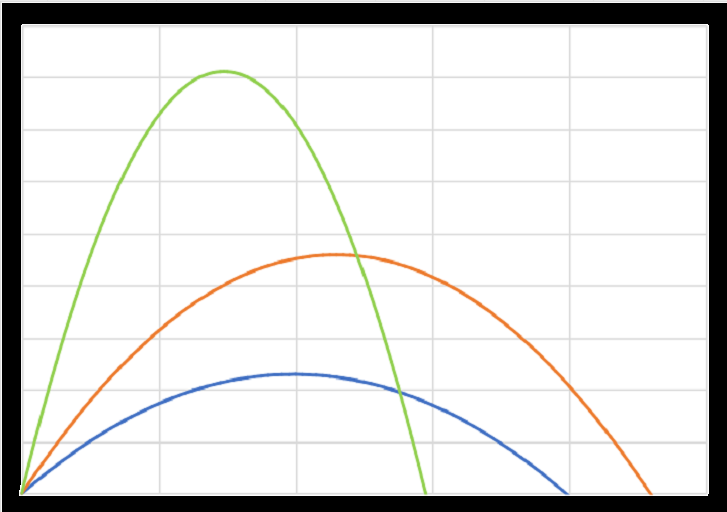
そういうことだな。この映画の式をロケットの発射角 \( \theta \) を横軸に、ロケットの飛距離 \( L \) を縦軸にしてグラフを書くと次のようになる。ただし、横軸の発射角は度数法で表しているから注意してくれな。
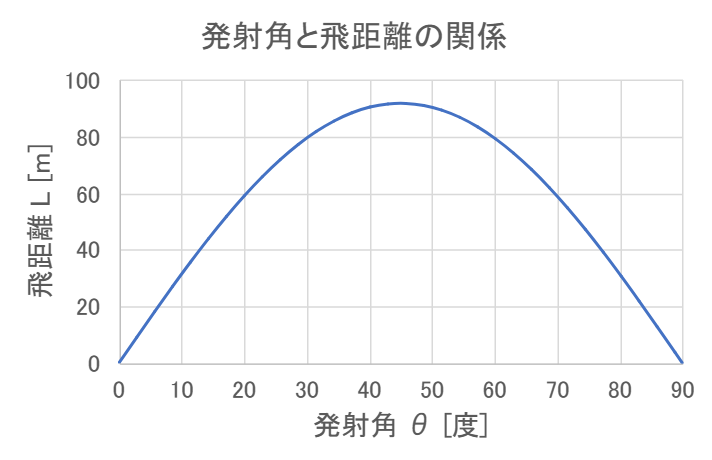
ナユミ
ふむ、斜め45°で一番飛距離が長くなるのね。そんな気がするわ。
カヤ
そんな気がするだろう。けど、今回は無視している空気抵抗の影響を考えると、実際にはそんなに簡単な話ではないだろうけどな。
ナユミ
そうなの？まあそれはまた今度のお楽しみね。
カヤ
そうだな。じゃあ、最後にせっかくなので実際の測定値に斜方投射の式を合わせた結果を紹介しておこう。
斜方投射の実験
カヤ
ボールを用意するのが面倒だったので、家にある靴下を丸めて斜めに放るという実験をしたぞ。
ナユミ
靴下…、ずいぶん生活感のある実験ね。
測定値の取得方法は、実験の様子を動画で撮影し、適当な時間間隔で動画を止めて、その時の靴下の位置を測定するというものです。測定値の取得に使った部分をスクリーンショットして切り取ってつなげたものが次の画像になります。
先ほどの放物線の式を測定値に合わせたものが次のグラフになります。
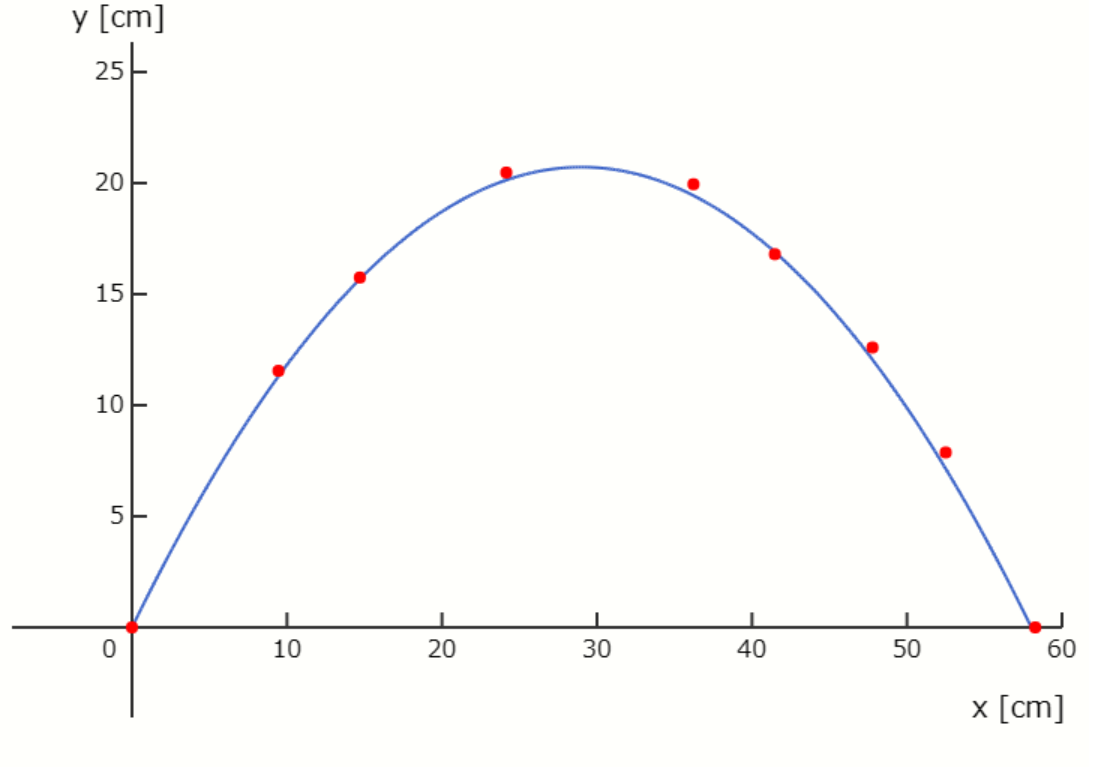
\( v_0 = 2.46 \rm \left[ m/s \right] \) 、\( g = 9.8 \rm \left[ m/ s^2 \right] \) 、\( \theta = 0.96 \) として計算。
ナユミ
すごい合ってるわね。
カヤ
まあな。このくらい小さな初速なら、空気抵抗の影響はほとんどないだろうから、かなりよく合っていると思う。
ナユミ
今までの数理モデルって、測定値の変化傾向は表せてるかなってぐらいだったけど、ちょっとこれは怖いぐらい一致してるわね。
カヤ
そうだな。この怖いくらいの一致があるから、ニュートンの運動方程式を基礎にした「ニュートン力学」という学問が成り立っているということだろうな。
ナユミ
ある一つの数理モデルっていう枠を超えて、一つの学問分野になっちゃったのね。出世したわね。
カヤ
そうだな。
参考：
[1] 塚本浩司、運動の第2法則はいつから運動方程式となったか？――19世紀英国の物理教科書にみる力学概念の変遷、日本物理学会誌、Voll.75、No.9、2020
[2] Paul G. Hewitt・John Suchocki・Leslie A. Hewitt著、小出昭一郎・吉田義久訳、物理科学のコンセプト１ 力と運動、共立出版、1997年6月15日発行
[3] The Feynman Lectures on Physics, Volume I, Chapter 9.Newton’s Laws of Dynamics、https://www.feynmanlectures.caltech.edu/I_09.html、2023年9月13日閲覧
[4] Wikipedia 重力加速度、https://ja.wikipedia.org/wiki/重力加速度、2023年9月14日閲覧
前の記事
第9話
流行語～SIRモデル～
流行語～SIRモデル～
前の記事
第11話
空気抵抗が
あるときの運動
空気抵抗が
あるときの運動