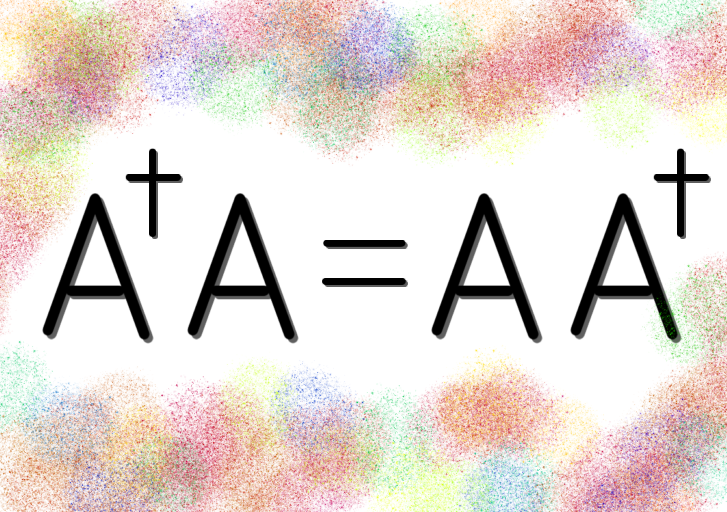
目次
・複素共軛行列と随伴行列
・正規行列
・エルミート行列
・ユニタリ行列
カヤ
今回は正規行列について解説する。まずは準備として複素共軛行列と随伴行列から見ていこう。
複素共軛行列と随伴行列
\[ 複素共軛行列\]
行列 \( A = \left( a_{ij} \right) \) の各成分を共軛複素数で置き換えた行列 \( \left( a_{ij} ^* \right) \) を \( A \)
の複素共軛行列と呼び、\( A^* \) で表す。
複素共軛行列について、以下が成り立ちます。
\[ \begin{align}
& \left( A^* \right) ^* = A \\\\
& \left( A + B \right) ^* = A^* + B^* \\\\
& \left( cA \right) ^* = c^* A^* \\\\
& \left( A B \right) ^* = A^* B^*
\end{align}\]
上の最後の式については、共軛複素数についての次の定理によります。
\[ 積の共軛は共軛同士の積\]
複素数 \( z_1 \) および \( z_2 \) について、
\[ \begin{align}
\left( z_1 z_2 \right) ^* = z_1 ^* z_2 ^*
\end{align}\]
が成り立つ。
\( i \) を虚数単位とし、\( z_1 = a + ib \) 、\( z_2 = c + id \) と置きます。
ただし、\( a \) 、\( b \) 、\( c \) 、\( d \) はいずれも実数とします。
\[ \begin{align}
z_1 z_2 = \left( ac - bd \right) + i \left( ad + bc \right)
\end{align}\]
なので、
\[ \begin{align}
\left( z_1 z_2 \right) ^* = \left( ac - bd \right) - i \left( ad + bc \right)
\end{align}\]
となります。一方、
\[ \begin{align}
z_1 ^* &= a - ib
= a + i \left( -b \right) \\\\
z_2 ^* &= c - id
= c + i \left( -d \right)
\end{align}\]
であることから、
\[ \begin{align}
z_1 ^* z_2 ^* &= \left\{ ac - \left( -b \right) \left( -d \right) \right\} + i \left\{ a \left( -d
\right) + \left( -b \right) c \right\} \\\\
&= \left( ac - bd \right) - i \left( ad + bc \right) \\\\
&= \left( z_1 z_2 \right) ^*
\end{align}\]
となり、上の定理が成り立ちます。
行列の積についても、各成分で上の定理が成り立つことから、\( \left( A B \right) ^* = A^* B^* \) が成り立ちます。
行列の積についても、各成分で上の定理が成り立つことから、\( \left( A B \right) ^* = A^* B^* \) が成り立ちます。
それから、転置行列について、以下が成り立つことも合わせて記しておきます。
\[ \begin{align}
& ^t \left( ^t A \right) = A \\\\
& ^t \left( A ^ * \right) = \left( ^t A \right) ^* \\\\
& ^t \left( A + B \right) = {}^tA + {}^tB \\\\
& ^t \left( cA \right) = c \ {}^t A \\\\
& ^t \left( A B \right) = {}^t B \ {}^t A
\end{align}\]
上の最後の式について確認しておきます。
\( A \) を \( \left( l, m \right) \) 型行列、\( B \) を \( \left( m, n \right) \) 型行列とし、
\[ \begin{align}
A = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1m} \\
a_{21} & a_{22} & \ldots & a_{2m} \\
\vdots & \vdots & & \vdots \\
a_{l1} & a_{l2} & \ldots & a_{lm}
\end{array}
\right)
, \ B = \left(
\begin{array}{cccc}
b_{11} & b_{12} & \ldots & b_{1n} \\
b_{21} & b_{22} & \ldots & b_{2n} \\
\vdots & \vdots & & \vdots \\
b_{m1} & b_{m2} & \ldots & b_{mn}
\end{array}
\right)
\end{align}\]
と表します。このとき、
\[ \begin{align}
AB = \left(
\begin{array}{cccc}
\sum _{j = 1} ^m a_{1j} b_{j1} & \sum _{j = 1} ^m a_{1j} b_{j2} & \ldots & \sum _{j = 1} ^m a_{1j}
b_{jn} \\
\sum _{j = 1} ^m a_{2j} b_{j1} & \sum _{j = 1} ^m a_{2j} b_{j2} & \ldots & \sum _{j = 1} ^m a_{2j}
b_{jn} \\
\vdots & \vdots & & \vdots \\
\sum _{j = 1} ^m a_{lj} b_{j1} & \sum _{j = 1} ^m a_{lj} b_{j2} & \ldots & \sum _{j = 1} ^m a_{lj}
b_{jn}
\end{array}
\right)
\end{align}\]
となるため、上の式の左辺は、
\[ \begin{align}
^t \left( A B \right) =
\left(
\begin{array}{cccc}
\sum _{j = 1} ^m a_{1j} b_{j1} & \sum _{j = 1} ^m a_{2j} b_{j1} & \ldots & \sum _{j = 1} ^m a_{lj}
b_{j1} \\
\sum _{j = 1} ^m a_{1j} b_{j2} & \sum _{j = 1} ^m a_{2j} b_{j2} & \ldots & \sum _{j = 1} ^m a_{lj}
b_{j2} \\
\vdots & \vdots & & \vdots \\
\sum _{j = 1} ^m a_{1j} b_{jn} & \sum _{j = 1} ^m a_{2j} b_{jn} & \ldots & \sum _{j = 1} ^m a_{lj}
b_{jn}
\end{array}
\right)
\end{align}\]
となり、\( ^t \left( A B \right) \) は \( \left( n, l \right) \) 型の行列となります。
一方、\( {}^t A \) は \( \left( m, l \right) \) 型の行列、\( {}^t B \) は \( \left( n, m \right) \) 型の行列であり、
\[ \begin{align}
{}^t A = \left(
\begin{array}{cccc}
a_{11} & a_{21} & \ldots & a_{l1} \\
a_{12} & a_{22} & \ldots & a_{l2} \\
\vdots & \vdots & & \vdots \\
a_{1m} & a_{2m} & \ldots & a_{lm}
\end{array}
\right)
, \ {}^t B = \left(
\begin{array}{cccc}
b_{11} & b_{21} & \ldots & b_{m1} \\
b_{12} & b_{22} & \ldots & b_{m2} \\
\vdots & \vdots & & \vdots \\
b_{1n} & b_{2n} & \ldots & b_{mn}
\end{array}
\right)
\end{align}\]
と表されます。ゆえに、行列の積 \( {}^t B \ {}^t A \) は定義され、これは \( ^t \left( A B \right) \) と等しくなります。
転置行列と複素共軛行列の概念を合わせて用いて、随伴行列が定義されます。
転置行列と複素共軛行列の概念を合わせて用いて、随伴行列が定義されます。
\[ 随伴行列\]
行列 \( A \) の複素共軛行列の転置行列 \( ^t \left( A ^* \right) \) を \( A \)
の随伴行列と呼び、\( A ^{\dagger} \) で表す。
随伴行列について、次が成り立ちます。
\[ \begin{align}
& \left( A ^{\dagger} \right) ^{\dagger} = A \\\\
& \left( A + B \right) ^{\dagger} = A ^{\dagger} + B ^{\dagger} \\\\
& \left( cA \right) ^{\dagger} = c^* A ^{\dagger} \\\\
& \left( A B \right) ^{\dagger} = B ^{\dagger} A ^{\dagger}
\end{align}\]
ナユミ
\( A ^{\dagger} \) って何て読むの？
カヤ
\( A \) の右上添え字はダガー（dagger）って読むんだ。短剣を意味する英語だな。
ナユミ
ふむ、言われてみると剣っぽいわね。
カヤ
そうだよな。それから、随伴行列と内積について次の関係がある。
\[ 随伴行列と内積\]
\( A \) を \( \left( m,n \right) \) 型行列とする。
このとき、任意の \( n \) 項列ベクトル \( \boldsymbol x \) と \( m \)
項列ベクトル \( \boldsymbol y \) に対して、
\[ \begin{align}
\left( A \boldsymbol x , \boldsymbol y \right) = \left( \boldsymbol x , A ^{\dagger} \boldsymbol y
\right)
\end{align}\]
が成り立つ。
逆に、任意の \( n \) 項列ベクトル \( \boldsymbol x \) と \( m \)
項列ベクトル \( \boldsymbol y \) に対して、
\[ \begin{align}
\left( A \boldsymbol x , \boldsymbol y \right) = \left( \boldsymbol x , B \boldsymbol y \right)
\end{align}\]
が成り立つとき、\( B = A ^{\dagger} \) である。
上の定理の前半部分は次の式変形より明らかです。
\[ \begin{align}
\left( A \boldsymbol x , \boldsymbol y \right) &= {}^t \left( A \boldsymbol x \right) \boldsymbol y^*
\\\\
&= {}^t \boldsymbol x {}^t A \boldsymbol y ^* \\\\
&= {}^t \boldsymbol x \left( {}^t A ^* \boldsymbol y \right) ^* \\\\
&= \left( \boldsymbol x , {}^t A ^* \boldsymbol y \right) \\\\
&= \left( \boldsymbol x , A ^{\dagger} \boldsymbol y \right)
\end{align}\]
後半部分は、前半部分の証明と条件より、
\[ \begin{align}
\left( \boldsymbol x , A ^{\dagger} \boldsymbol y \right) = \left( \boldsymbol x , B \boldsymbol y
\right)
\end{align}\]
が成り立つため、両辺を比較して \( B = A ^{\dagger} \) が示せます。
カヤ
じゃあ、次は随伴行列を用いて正規行列を定義しよう。
正規行列
\[ 正規行列\]
正方行列 \( A \) が \( A ^{\dagger} A = A A ^{\dagger} \) を満たすとき、\( A \) を正規行列と呼ぶ。
正規行列の定義にある条件は、ノルムについての次の条件と同値です。
\[ 正規行列とノルム\]
\( n \) 次正方行列 \( A \) が \( A ^{\dagger} A = A A ^{\dagger} \) を満たすための必要十分条件は、任意の \( n \) 項列ベクトル \(
\boldsymbol x \) に対して、
\[ \begin{align}
\| A \boldsymbol x \| = \| A ^{\dagger} \boldsymbol x \|
\end{align}\]
が成り立つことである。
まずは、\( A ^{\dagger} A = A A ^{\dagger} \) が成り立つと仮定します。ノルムの定義より、
\[ \begin{align}
\| A \boldsymbol x \| ^2 &= \left( A \boldsymbol x , A \boldsymbol x \right) \\\\
&= \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) \\\\
\| A ^{\dagger} \boldsymbol x \| ^2 &= \left( A ^{\dagger} \boldsymbol x , A ^{\dagger} \boldsymbol x
\right) \\\\
&= \left( \boldsymbol x , \left( A ^{\dagger} \right) ^{\dagger} A ^{\dagger} \boldsymbol x \right) \\\\
&= \left( \boldsymbol x , A A ^{\dagger} \boldsymbol x \right)
\end{align}\]
が成り立つため、仮定より、
\[ \begin{align}
\| A \boldsymbol x \| ^2 =
\| A ^{\dagger} \boldsymbol x \| ^2
\end{align}\]
となり、この式の両辺について平方根を取れば \( \| A \boldsymbol x \| = \| A ^{\dagger} \boldsymbol x \| \) が示せます。
逆に、\( \| A \boldsymbol x \| = \| A ^{\dagger} \boldsymbol x \| \) が成り立つと仮定した場合は、上の証明で用いた式変形より、 \[ \begin{align} \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) = \left( \boldsymbol x , A A ^{\dagger} \boldsymbol x \right) \end{align}\] が成り立つため、この式の両辺を比較すれば、\( A ^{\dagger} A = A A ^{\dagger} \) が成り立つことが示せます。
正規行列は次に挙げるエルミート行列およびユニタリ行列を包括する概念です。
逆に、\( \| A \boldsymbol x \| = \| A ^{\dagger} \boldsymbol x \| \) が成り立つと仮定した場合は、上の証明で用いた式変形より、 \[ \begin{align} \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) = \left( \boldsymbol x , A A ^{\dagger} \boldsymbol x \right) \end{align}\] が成り立つため、この式の両辺を比較すれば、\( A ^{\dagger} A = A A ^{\dagger} \) が成り立つことが示せます。
正規行列は次に挙げるエルミート行列およびユニタリ行列を包括する概念です。
ナユミ
エルミート行列とユニタリ行列って？
カヤ
まずはエルミート行列を見ていこう。
エルミート行列
\[ \begin{align}
エルミート行列
\end{align}\]
正方行列 \( A \) が \( A = A ^{\dagger} \) を満たすとき、\( A \) をエルミート行列と呼ぶ。
特に、実行列であるエルミート行列を実対称行列と呼ぶ。
\( A \) がエルミート行列であるとき、
\[ \begin{align}
A^2 = A ^{\dagger} A = A A ^{\dagger}
\end{align}\]
が成り立つため、\( A \) は正規行列でもあります。
また、エルミート行列の定義にある条件 \( A = A ^{\dagger} \) は、随伴行列と内積についての定理より、 任意の列ベクトル \( \boldsymbol x \) と \( \boldsymbol y \) に対して、 \[ \begin{align} \left( A \boldsymbol x , \boldsymbol y \right) = \left( \boldsymbol x , A \boldsymbol y \right) \end{align}\] が成り立つことと同値です。
行列とその転置行列の対角成分は等しいため、\( A = A ^{\dagger} \) の条件から、エルミート行列の対角成分はその共軛複素数と等しいことになります。 これは、エルミート行列の対角成分がすべて実数であることを意味しています。
さらに、エルミート行列の固有値と行列式について、次が成り立ちます。
また、エルミート行列の定義にある条件 \( A = A ^{\dagger} \) は、随伴行列と内積についての定理より、 任意の列ベクトル \( \boldsymbol x \) と \( \boldsymbol y \) に対して、 \[ \begin{align} \left( A \boldsymbol x , \boldsymbol y \right) = \left( \boldsymbol x , A \boldsymbol y \right) \end{align}\] が成り立つことと同値です。
行列とその転置行列の対角成分は等しいため、\( A = A ^{\dagger} \) の条件から、エルミート行列の対角成分はその共軛複素数と等しいことになります。 これは、エルミート行列の対角成分がすべて実数であることを意味しています。
さらに、エルミート行列の固有値と行列式について、次が成り立ちます。
\[ \begin{align}
エルミート行列の固有値と行列式
\end{align}\]
エルミート行列の固有値および行列式はすべて実数である。
\( A \) をエルミート行列、\( \lambda \) を \( A \) の固有値、\( \boldsymbol x \) を \( \lambda \) に対する固有ベクトルとします。
固有値方程式より、
\[ \begin{align}
A \boldsymbol x = \lambda \boldsymbol x
\end{align}\]
が成り立ちます。この式の両辺に左から \( \boldsymbol x ^{\dagger} \) をかけて、
\[ \begin{align}
\boldsymbol x ^{\dagger} A \boldsymbol x = \lambda \boldsymbol x ^{\dagger} \boldsymbol x \ \cdots
\left( 1 \right)
\end{align}\]
を得ます。\( \left( 1 \right) \) 式の両辺の随伴行列を考えると、
\[ \begin{align}
\left( \boldsymbol x ^{\dagger} A \boldsymbol x \right) ^{\dagger} &= \left( \lambda \boldsymbol x
^{\dagger} \boldsymbol x \right) ^{\dagger} \\\\
\left( \left( \boldsymbol x ^{\dagger} A \right) \boldsymbol x \right) ^{\dagger} &= \lambda ^* \left(
\boldsymbol x ^{\dagger} \boldsymbol x \right) ^{\dagger} \\\\
\boldsymbol x ^{\dagger} \left( \boldsymbol x ^{\dagger} A \right) ^{\dagger} &= \lambda ^* \boldsymbol
x ^{\dagger} \left( \boldsymbol x ^{\dagger} \right) ^{\dagger} \\\\
\boldsymbol x ^{\dagger} A ^{\dagger} \left( \boldsymbol x ^{\dagger} \right) ^{\dagger} &= \lambda ^*
\boldsymbol x ^{\dagger} \boldsymbol x \\\\
\boldsymbol x ^{\dagger} A ^{\dagger} \boldsymbol x &= \lambda ^* \boldsymbol x ^{\dagger} \boldsymbol x
\end{align}\]
ここで、\( A = A ^{\dagger} \) より、
\[ \begin{align}
\boldsymbol x ^{\dagger} A \boldsymbol x &= \lambda ^* \boldsymbol x ^{\dagger} \boldsymbol x \ \cdots
\left( 2 \right)
\end{align}\]
を得ます。\( \left( 1 \right) \) 式と \( \left( 2 \right) \) 式より、
\[ \begin{align}
\left( \lambda - \lambda ^* \right) \boldsymbol x ^{\dagger} \boldsymbol x = 0
\end{align}\]
を得ます。\( \boldsymbol x \neq 0 \) であるため、\( \lambda = \lambda ^* \) となることから、\( \lambda \) は実数となります。
さらに、行列式はすべての固有値の積であるので、エルミート行列の行列式も実数となります。
ナユミ
そういえば、エルミートって人の名前かな？
カヤ
ああ。エルミートはフランスの数学者だ。
シャルル・エルミートは19世紀に活躍したフランスの数学者です。
楕円関数を用いた5次方程式の解の公式の発見や、
ネイピア数 \( e \) が超越数であることを初めて証明したことでも知られています。
シャルル・エルミート(1822-1901)
カヤ
じゃあ、あとはユニタリ行列を見ておこう。
ユニタリ行列
\[ ユニタリ行列\]
正方行列 \( A \) が、\( A A ^{\dagger} = E \) を満たすとき、\( A \) をユニタリ行列と呼ぶ。
特に、実行列であるユニタリ行列を直交行列と呼ぶ。
右逆行列の存在と正則性についての定理より、ユニタリ行列は正則で、逆行列が存在します。
よって、ユニタリ行列の条件は、
\[ \begin{align}
A A ^{\dagger} &= E \\\\
A A ^{\dagger} A &= EA = A \\\\
A^{-1} A A ^{\dagger} A &= A^{-1} A \\\\
A ^{\dagger} A &= E
\end{align}\]
と変形できます。
もし、\( A ^{\dagger} A = E \) を仮定した場合は、左逆行列の存在と正則性についての定理からユニタリ行列の正則性が言えて、
上の変形を逆にたどれば \( A A ^{\dagger} = E \) が導けます。
よって、\( A ^{\dagger} A = E \) をユニタリ行列の定義に用いても構いません。
また、
\[ \begin{align}
A ^{\dagger} A = A A ^{\dagger} = E
\end{align}\]
が成り立つことより、
\[ \begin{align}
A ^{-1} = A ^{\dagger}
\end{align}\]
となります。また、ここで \( A ^{\dagger} A = A A ^{\dagger} \) が成り立つことより、ユニタリ行列が正規行列であることもわかります。
\( A \) と \( B \) がユニタリ行列なら、積 \( AB \) および \( BA \) もユニタリ行列になります。これは、 \[ \begin{align} \left( AB \right) \left( AB \right) ^{\dagger} &= \left( AB \right) \left( B ^{\dagger} A ^{\dagger} \right) = E \\\\ \left( BA \right) \left( BA \right) ^{\dagger} &= \left( BA \right) \left( A ^{\dagger} B ^{\dagger} \right) = E \end{align}\] を示せばよいです。また、\( A \) がユニタリ行列なら、\( A ^{\dagger} A = E \) および \( A ^{-1} = A ^{\dagger} \) が成り立つので、\( A^{-1} \) もユニタリ行列になります。
ユニタリ行列の条件式には、次の 3 つの同値な条件があります。
\( A \) と \( B \) がユニタリ行列なら、積 \( AB \) および \( BA \) もユニタリ行列になります。これは、 \[ \begin{align} \left( AB \right) \left( AB \right) ^{\dagger} &= \left( AB \right) \left( B ^{\dagger} A ^{\dagger} \right) = E \\\\ \left( BA \right) \left( BA \right) ^{\dagger} &= \left( BA \right) \left( A ^{\dagger} B ^{\dagger} \right) = E \end{align}\] を示せばよいです。また、\( A \) がユニタリ行列なら、\( A ^{\dagger} A = E \) および \( A ^{-1} = A ^{\dagger} \) が成り立つので、\( A^{-1} \) もユニタリ行列になります。
ユニタリ行列の条件式には、次の 3 つの同値な条件があります。
\[ ユニタリ行列の同値条件\]
\( n \) 次正方行列に関する次の 4 つの条件は同値である。
[1] \( A \) はユニタリ行列である。すなわち、次が成り立つ。 \[ \begin{align} A A ^{\dagger} = A ^{\dagger} A = E \end{align}\] [2] 任意の \( n \) 項列ベクトル \( \boldsymbol x \) に対して、次が成り立つ。 \[ \begin{align} \| A \boldsymbol x \| = \| \boldsymbol x \| \end{align}\] [3] 任意の \( n \) 項列ベクトル \( \boldsymbol x \) および \( \boldsymbol y \) に対して、次が成り立つ。 \[ \begin{align} \left( A \boldsymbol x , A \boldsymbol y \right) = \left( \boldsymbol x , \boldsymbol y \right) \end{align}\] [4] \( A \) の列ベクトルを \( \boldsymbol a_1 , \boldsymbol a_2 , \cdots , \boldsymbol a_n \) とするとき、次が成り立つ。 \[ \begin{align} \left( \boldsymbol a_i , \boldsymbol a_j \right) = \delta _{ij} = \left\{ \begin{array}{l} 1 \ \ \ \left( i=j \right) \\ 0 \ \ \ \left( i \neq j \right) \end{array} \right. \end{align}\]
[1] \( A \) はユニタリ行列である。すなわち、次が成り立つ。 \[ \begin{align} A A ^{\dagger} = A ^{\dagger} A = E \end{align}\] [2] 任意の \( n \) 項列ベクトル \( \boldsymbol x \) に対して、次が成り立つ。 \[ \begin{align} \| A \boldsymbol x \| = \| \boldsymbol x \| \end{align}\] [3] 任意の \( n \) 項列ベクトル \( \boldsymbol x \) および \( \boldsymbol y \) に対して、次が成り立つ。 \[ \begin{align} \left( A \boldsymbol x , A \boldsymbol y \right) = \left( \boldsymbol x , \boldsymbol y \right) \end{align}\] [4] \( A \) の列ベクトルを \( \boldsymbol a_1 , \boldsymbol a_2 , \cdots , \boldsymbol a_n \) とするとき、次が成り立つ。 \[ \begin{align} \left( \boldsymbol a_i , \boldsymbol a_j \right) = \delta _{ij} = \left\{ \begin{array}{l} 1 \ \ \ \left( i=j \right) \\ 0 \ \ \ \left( i \neq j \right) \end{array} \right. \end{align}\]
★[1] と [2] が同値であることの証明
まずは、[1] から [2] を示します。ノルムの定義より、 \[ \begin{align} \| A \boldsymbol x \| ^2 &= \left( A \boldsymbol x , A \boldsymbol x \right) \\\\ &= \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) \end{align}\] ここで、[1] より \( A ^{\dagger} A = E \) であるため、 \[ \begin{align} \| A \boldsymbol x \| ^2 = \left( \boldsymbol x , \boldsymbol x \right) = \| \boldsymbol x \| ^2 \end{align}\] よって、この式の両辺の平方根を取れば [2] が示されます。 次に、[2] から [1] を示します。\( \| A \boldsymbol x \| = \| \boldsymbol x \| \) より、 \[ \begin{align} \| A \boldsymbol x \| ^2 &= \| \boldsymbol x \| ^2 \\\\ \left( A \boldsymbol x , A \boldsymbol x \right) &= \left( \boldsymbol x , \boldsymbol x \right) \\\\ \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) &= \left( \boldsymbol x , \boldsymbol x \right) \end{align}\] 両辺の比較から、\( A ^{\dagger} A = E \) であり、これより \( A \) はユニタリ行列となるため [1] が示されました。 以上より、[1] と [2] は同値であることが証明できました。
★[1] と [3] が同値であることの証明
まずは、[1] から [3] を示します。\( A ^{\dagger} A = E \) に注意して、 \[ \begin{align} \left( A \boldsymbol x , A \boldsymbol y \right) = \left( \boldsymbol x , A ^{\dagger} A \boldsymbol y \right) = \left( \boldsymbol x , \boldsymbol y \right) \end{align}\] 逆に、[3] から [1] を示すには、 \[ \begin{align} \left( \boldsymbol x , A ^{\dagger} A \boldsymbol y \right) = \left( \boldsymbol x , \boldsymbol y \right) \end{align}\] の両辺を比較すればよいです。
★[1] と [4] が同値であることの証明
まず、 \[ \begin{align} A ^{\dagger} A &= E \\\\ \left( A ^{\dagger} A \right) ^* &= E^* \\\\ {}^t A A^* &= E \end{align}\] と変形できることより、\( {}^t A A^* = E \) と [1] は同値であることに注意します。そして、 \[ \begin{align} {}^t A A^* &= \left( \begin{array}{cccc} a_{11} & a_{21} & \ldots & a_{n1} \\ a_{12} & a_{22} & \ldots & a_{n2} \\ \vdots & \vdots & & \vdots \\ a_{1n} & a_{2n} & \ldots & a_{nn} \end{array} \right) \left( \begin{array}{cccc} {a_{11}} ^* & {a_{12}} ^* & \ldots & {a_{1n}} ^* \\ {a_{21}} ^* & {a_{22}} ^* & \ldots & {a_{2n}} ^*\\ \vdots & \vdots & & \vdots \\ {a_{n1}} ^* & {a_{n2}} ^* & \ldots & {a_{nn}} ^* \end{array} \right) \\\\ &= \left( \begin{array}{cccc} \left( \boldsymbol a_1 , \boldsymbol a_1 \right) & \left( \boldsymbol a_1 , \boldsymbol a_2 \right) & \ldots & \left( \boldsymbol a_1 , \boldsymbol a_n \right) \\ \left( \boldsymbol a_2 , \boldsymbol a_1 \right) & \left( \boldsymbol a_2 , \boldsymbol a_2 \right) & \ldots & \left( \boldsymbol a_2 , \boldsymbol a_n \right) \\ \vdots & \vdots & & \vdots \\ \left( \boldsymbol a_n , \boldsymbol a_1 \right) & \left( \boldsymbol a_n , \boldsymbol a_2 \right) & \ldots & \left( \boldsymbol a_n , \boldsymbol a_n \right) \end{array} \right) \end{align}\] であるため、[4] と \( {}^t A A^* = E \) は同値となります。 よって、[1] と [4] は同値であると言えます。
まずは、[1] から [2] を示します。ノルムの定義より、 \[ \begin{align} \| A \boldsymbol x \| ^2 &= \left( A \boldsymbol x , A \boldsymbol x \right) \\\\ &= \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) \end{align}\] ここで、[1] より \( A ^{\dagger} A = E \) であるため、 \[ \begin{align} \| A \boldsymbol x \| ^2 = \left( \boldsymbol x , \boldsymbol x \right) = \| \boldsymbol x \| ^2 \end{align}\] よって、この式の両辺の平方根を取れば [2] が示されます。 次に、[2] から [1] を示します。\( \| A \boldsymbol x \| = \| \boldsymbol x \| \) より、 \[ \begin{align} \| A \boldsymbol x \| ^2 &= \| \boldsymbol x \| ^2 \\\\ \left( A \boldsymbol x , A \boldsymbol x \right) &= \left( \boldsymbol x , \boldsymbol x \right) \\\\ \left( \boldsymbol x , A ^{\dagger} A \boldsymbol x \right) &= \left( \boldsymbol x , \boldsymbol x \right) \end{align}\] 両辺の比較から、\( A ^{\dagger} A = E \) であり、これより \( A \) はユニタリ行列となるため [1] が示されました。 以上より、[1] と [2] は同値であることが証明できました。
★[1] と [3] が同値であることの証明
まずは、[1] から [3] を示します。\( A ^{\dagger} A = E \) に注意して、 \[ \begin{align} \left( A \boldsymbol x , A \boldsymbol y \right) = \left( \boldsymbol x , A ^{\dagger} A \boldsymbol y \right) = \left( \boldsymbol x , \boldsymbol y \right) \end{align}\] 逆に、[3] から [1] を示すには、 \[ \begin{align} \left( \boldsymbol x , A ^{\dagger} A \boldsymbol y \right) = \left( \boldsymbol x , \boldsymbol y \right) \end{align}\] の両辺を比較すればよいです。
★[1] と [4] が同値であることの証明
まず、 \[ \begin{align} A ^{\dagger} A &= E \\\\ \left( A ^{\dagger} A \right) ^* &= E^* \\\\ {}^t A A^* &= E \end{align}\] と変形できることより、\( {}^t A A^* = E \) と [1] は同値であることに注意します。そして、 \[ \begin{align} {}^t A A^* &= \left( \begin{array}{cccc} a_{11} & a_{21} & \ldots & a_{n1} \\ a_{12} & a_{22} & \ldots & a_{n2} \\ \vdots & \vdots & & \vdots \\ a_{1n} & a_{2n} & \ldots & a_{nn} \end{array} \right) \left( \begin{array}{cccc} {a_{11}} ^* & {a_{12}} ^* & \ldots & {a_{1n}} ^* \\ {a_{21}} ^* & {a_{22}} ^* & \ldots & {a_{2n}} ^*\\ \vdots & \vdots & & \vdots \\ {a_{n1}} ^* & {a_{n2}} ^* & \ldots & {a_{nn}} ^* \end{array} \right) \\\\ &= \left( \begin{array}{cccc} \left( \boldsymbol a_1 , \boldsymbol a_1 \right) & \left( \boldsymbol a_1 , \boldsymbol a_2 \right) & \ldots & \left( \boldsymbol a_1 , \boldsymbol a_n \right) \\ \left( \boldsymbol a_2 , \boldsymbol a_1 \right) & \left( \boldsymbol a_2 , \boldsymbol a_2 \right) & \ldots & \left( \boldsymbol a_2 , \boldsymbol a_n \right) \\ \vdots & \vdots & & \vdots \\ \left( \boldsymbol a_n , \boldsymbol a_1 \right) & \left( \boldsymbol a_n , \boldsymbol a_2 \right) & \ldots & \left( \boldsymbol a_n , \boldsymbol a_n \right) \end{array} \right) \end{align}\] であるため、[4] と \( {}^t A A^* = E \) は同値となります。 よって、[1] と [4] は同値であると言えます。
ナユミ
同値な条件がたくさんあるわね。
カヤ
そうだな。あとは、ユニタリ行列の固有値と行列式について次の定理がある。
\[ \begin{align}
ユニタリ行列の固有値と行列式
\end{align}\]
ユニタリ行列の固有値および行列式は絶対値が 1 の複素数である。
\( A \) をユニタリ行列、\( \lambda \) を \( A \) の固有値、\( \boldsymbol x \) を \( \lambda \) に対する固有ベクトルとします。
固有値方程式より、
\[ \begin{align}
A \boldsymbol x = \lambda \boldsymbol x
\end{align}\]
が成り立ちます。よって、両辺のノルムを考えると、
\[ \begin{align}
\| A \boldsymbol x \| &= \| \lambda \boldsymbol x \| \\\\
&= \sqrt{\left( \lambda \boldsymbol x , \lambda \boldsymbol x \right)} \\\\
&= \sqrt{\lambda \lambda ^* \left( \boldsymbol x , \boldsymbol x \right)} \\\\
&= \sqrt{| \lambda | ^2 \left( \boldsymbol x , \boldsymbol x \right)} \\\\
&= | \lambda | \| \boldsymbol x \| \ \ \ \ \ldots \left( 3 \right)
\end{align}\]
が成り立ちます。一方、ユニタリ行列の同値条件 [2] より、
\[ \begin{align}
\| A \boldsymbol x \| = \| \boldsymbol x \| \ \ldots \left( 4 \right)
\end{align}\]
であるため、\( \left( 3 \right) \) 式と \( \left( 4 \right) \) 式より、
\[ \begin{align}
| \lambda | \| \boldsymbol x \| = \| \boldsymbol x \|
\end{align}\]
が成り立ちます。よって、\( | \lambda | = 1 \) となります。
行列式については、\( A \) を \( n \) 次ユニタリ行列とすれば、その固有値 \( \lambda _j \) は絶対値が 1 であることより、 \[ \begin{align} \lambda _j = \cos \theta _j + i \sin \theta _j = e^{i \theta_j} \ \ \ \left( j = 1, 2, \cdots , n \right) \end{align}\] という形で表せるため、 \[ \begin{align} | A | &= \lambda _1 \lambda _2 \cdots \lambda _n \\\\ &= e^{i \theta_1} e^{i \theta_2} \cdots e^{i \theta_n} \\\\ &= e^{i \left( \theta_1 + \theta_2 + \cdots + \theta_n \right) } \end{align}\] となり、行列式の絶対値も 1 であるとわかります。
行列式については、\( A \) を \( n \) 次ユニタリ行列とすれば、その固有値 \( \lambda _j \) は絶対値が 1 であることより、 \[ \begin{align} \lambda _j = \cos \theta _j + i \sin \theta _j = e^{i \theta_j} \ \ \ \left( j = 1, 2, \cdots , n \right) \end{align}\] という形で表せるため、 \[ \begin{align} | A | &= \lambda _1 \lambda _2 \cdots \lambda _n \\\\ &= e^{i \theta_1} e^{i \theta_2} \cdots e^{i \theta_n} \\\\ &= e^{i \left( \theta_1 + \theta_2 + \cdots + \theta_n \right) } \end{align}\] となり、行列式の絶対値も 1 であるとわかります。
ナユミ
絶対値が 1 、だから Unitary なのね。
カヤ
そういうことだな。
参考：
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行
[2] 和達三樹、物理のための数学 （物理入門コース10）、岩波書店、1983年3月14日発行
[3] Wikipedia Charles Hermite、https://en.wikipedia.org/wiki/Charles_Hermite、2024年11月29日閲覧
前の記事
第40話
固有値
固有値
次の記事
第42話
線形独立
線形独立