目次
・基本行列
・掃出し
・階数
・階数と正則性の関係
基本行列
次に示す、3 種類の正則行列を基本行列と呼び、行列 \( A \) の左あるいは右から基本行列をかけることを、
左基本変形あるいは右基本変形と呼びます。左基本変形と右基本変形を合わせて基本変形と呼びます。
[1] \( n \) 次単位行列の、第 \( i \) 列と第 \( j \) 列とを交換した行列 \( P_n \left( i , j \right) \)
\( \left( m, n \right) \) 型行列 \( A \) に対し、\( P_m \left( i , j \right) \) を左からかけると、\( A \) の第 \( i \) 行と第 \( j \) 行とが交換されます。 一方、\( P_n \left( i , j \right) \) を右からかけると、\( A \) の第 \( i \) 列と第 \( j \) 列とが交換されます。
[2] \( n \) 次単位行列の \( \left( i, i \right) \) 成分を、0 でない数 \( c \) に変えた行列 \( Q_n \left( i ; \ c \right) \)
\( \left( m, n \right) \) 型行列 \( A \) に対し、\( Q_m \left( i ; \ c \right) \) を左からかけると、\( A \) の第 \( i \) 行が \( c \) 倍されます。 一方、\( Q_n \left( i ; \ c \right) \) を右からかけると、\( A \) の第 \( i \) 列が \( c \) 倍されます。
[3] \( n \) 次単位行列の \( \left( i, j \right) \) 成分 \( \left( i \neq j \right) \) を、数 \( c \) に変えた行列 \( R_n \left( i,j ; \ c \right) \)
\( \left( m, n \right) \) 型行列 \( A \) に対し、\( R_m \left( i,j ; \ c \right) \) を左からかけると、\( A \) の第 \( i \) 行に第 \( j \) 行の \( c \) 倍が加わります。 一方、\( R_n \left( i,j ; \ c \right) \) を右からかけると、\( A \) の第 \( j \) 列に第 \( i \) 列の \( c \) 倍が加わります。
[1] \( n \) 次単位行列の、第 \( i \) 列と第 \( j \) 列とを交換した行列 \( P_n \left( i , j \right) \)
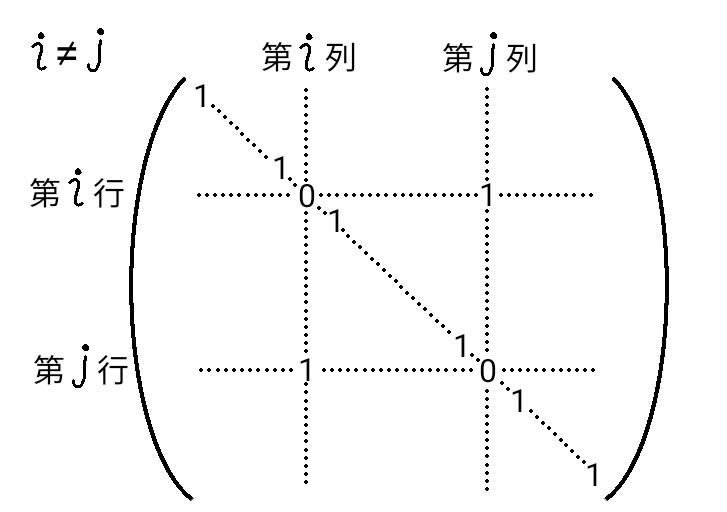
\( \left( m, n \right) \) 型行列 \( A \) に対し、\( P_m \left( i , j \right) \) を左からかけると、\( A \) の第 \( i \) 行と第 \( j \) 行とが交換されます。 一方、\( P_n \left( i , j \right) \) を右からかけると、\( A \) の第 \( i \) 列と第 \( j \) 列とが交換されます。
[2] \( n \) 次単位行列の \( \left( i, i \right) \) 成分を、0 でない数 \( c \) に変えた行列 \( Q_n \left( i ; \ c \right) \)

\( \left( m, n \right) \) 型行列 \( A \) に対し、\( Q_m \left( i ; \ c \right) \) を左からかけると、\( A \) の第 \( i \) 行が \( c \) 倍されます。 一方、\( Q_n \left( i ; \ c \right) \) を右からかけると、\( A \) の第 \( i \) 列が \( c \) 倍されます。
[3] \( n \) 次単位行列の \( \left( i, j \right) \) 成分 \( \left( i \neq j \right) \) を、数 \( c \) に変えた行列 \( R_n \left( i,j ; \ c \right) \)

\( \left( m, n \right) \) 型行列 \( A \) に対し、\( R_m \left( i,j ; \ c \right) \) を左からかけると、\( A \) の第 \( i \) 行に第 \( j \) 行の \( c \) 倍が加わります。 一方、\( R_n \left( i,j ; \ c \right) \) を右からかけると、\( A \) の第 \( j \) 列に第 \( i \) 列の \( c \) 倍が加わります。
掃出し
\( \left( m, n \right) \) 型行列 \( A \) の \( \left( p, q \right) \) 成分が 0 でないとき、この成分を 1
にし、この成分を中心とした十字型の成分をすべて 0 とするような変形を考えます。
まず、第 \( p \) 行を \( \left( p, q \right) \) 成分で割り、\( \left( p, q \right) \) 成分を 1 にします。 次に、\( p \) 以外のすべての \( i \) に対し、第 \( i \) 行から第 \( p \) 行の \( \left( i, q \right) \) 成分倍を引きます。 これにより、行列 \( A \) は次の \( A' \) に変形されます。
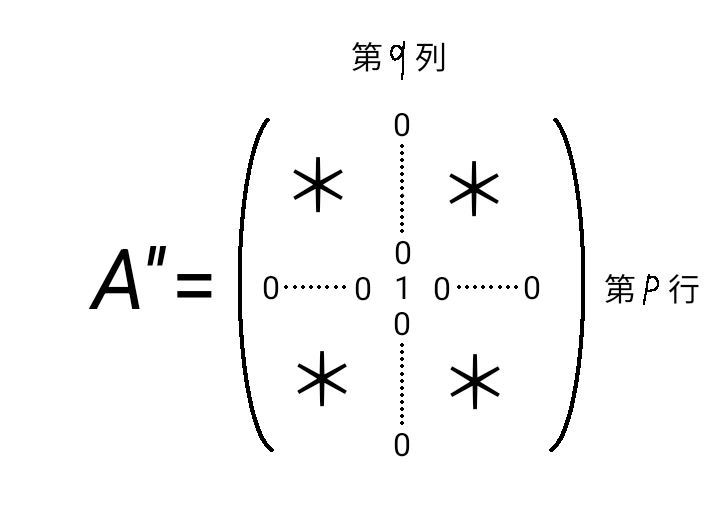
続いて、\( A' \) について、\( q \) 以外のすべての \( j \) に対し、第 \( j \) 列から第 \( q \) 列の \( \left( p, j \right) \) 成分倍を引けば、\( A' \) は次の \( A'' \) に変形されます。
まず、第 \( p \) 行を \( \left( p, q \right) \) 成分で割り、\( \left( p, q \right) \) 成分を 1 にします。 次に、\( p \) 以外のすべての \( i \) に対し、第 \( i \) 行から第 \( p \) 行の \( \left( i, q \right) \) 成分倍を引きます。 これにより、行列 \( A \) は次の \( A' \) に変形されます。

続いて、\( A' \) について、\( q \) 以外のすべての \( j \) に対し、第 \( j \) 列から第 \( q \) 列の \( \left( p, j \right) \) 成分倍を引けば、\( A' \) は次の \( A'' \) に変形されます。
\[ \begin{align}
左(右)逆行列の存在と正則性
\end{align}\]
\( n \) 次正方行列 \( A \) に対し、\( XA = E \) となる \( n \) 次行列 \( X \) が存在すれば \( A \) は正則である。
\( AX = E \) となる \( X \) の存在を仮定しても同様に \( A \) は正則である。
この定理の証明には \( n \) についての数学的帰納法を用います。
\( n = 1 \) 、つまり \( 1 \) 次正方行列については、行列の積は普通のかけ算と同じになるので、定理は成り立ちます。
そこで、\( n \gt 1 \) とし、\( n - 1 \) 次行列に対して定理が成り立つと仮定します。
まず、\( XA = E \) となる \( n \) 次行列 \( X \) が存在する場合について考えます。 \( XA = E \) の条件より、\( A \) は零行列ではないため、必要であれば行および列の交換を行い、 \( \left( 1,1 \right) \) 成分が 0 でなくなるように基本変形を施します。 その後、\( \left( 1,1 \right) \) をかなめとして左右から第 1 列、第 1 行を掃出すと、 行列 \( A \) は次の行列 \( B \) に変形されます。 \[ \begin{align} B = \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \end{align}\] ここで、\( A_1 \) は \( n - 1 \) 次行列です。 このことを言い換えると、適当な正則行列 \( P \) と \( Q \) を用いて、 \[ \begin{align} PAQ = B = \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \end{align}\] となるようにできる、ということでもあります。 \( B \) の区分けに応じて、\( Q^{-1} X P^{-1} \) を次のように区分けします。 \[ \begin{align} Q^{-1} X P^{-1} = \left( \begin{array}{cc} u & z \\ y & X_1 \\ \end{array} \right) \end{align}\] ここで、\( u \) は \( \left( 1,1 \right) \) 成分です。また、\( X_1 \) は \( n - 1 \) 次行列、\( y \) は \( n - 1 \) 項列ベクトル、\( z \) は \( n - 1 \) 項行ベクトルです。 \[ \begin{align} \left( Q^{-1} X P^{-1} \right) \left( PAQ \right) = E \end{align}\] が成り立つため、 \[ \begin{align} \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & E_{n-1} \\ \end{array} \right) &= \left( \begin{array}{cc} u & z \\ y & X_1 \\ \end{array} \right) \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \\\\ &= \left( \begin{array}{cc} u & zA_{1} \\ y & X_1 A_1 \\ \end{array} \right) \end{align}\] よって、 \[ \begin{align} X_1 A_1 = E_{n-1} \end{align}\] が成り立ちます。この式と、帰納法の仮定より、\( A_1 \) は正則と言えます。 よって、対称区分けされた正方行列の正則性についての定理より、\( B \) も正則となります。 すると、\( A = P^{-1} B Q^{-1} \) であるので \( A \) も正則となります。
\( AX = E \) となる \( n \) 次行列 \( X \) が存在する場合は、 \[ \begin{align} \left( PAQ \right) \left( Q^{-1} X P^{-1} \right) = E \end{align}\] となることから、 \[ \begin{align} \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & E_{n-1} \\ \end{array} \right) &= \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \left( \begin{array}{cc} u & z \\ y & X_1 \\ \end{array} \right) \\\\ &= \left( \begin{array}{cc} u & z \\ A_1 y & A_1 X_1 \\ \end{array} \right) \end{align}\] が成り立ち、あとは \( XA = E \) となる \( n \) 次行列 \( X \) が存在する場合と同様の手順で証明できます。
まず、\( XA = E \) となる \( n \) 次行列 \( X \) が存在する場合について考えます。 \( XA = E \) の条件より、\( A \) は零行列ではないため、必要であれば行および列の交換を行い、 \( \left( 1,1 \right) \) 成分が 0 でなくなるように基本変形を施します。 その後、\( \left( 1,1 \right) \) をかなめとして左右から第 1 列、第 1 行を掃出すと、 行列 \( A \) は次の行列 \( B \) に変形されます。 \[ \begin{align} B = \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \end{align}\] ここで、\( A_1 \) は \( n - 1 \) 次行列です。 このことを言い換えると、適当な正則行列 \( P \) と \( Q \) を用いて、 \[ \begin{align} PAQ = B = \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \end{align}\] となるようにできる、ということでもあります。 \( B \) の区分けに応じて、\( Q^{-1} X P^{-1} \) を次のように区分けします。 \[ \begin{align} Q^{-1} X P^{-1} = \left( \begin{array}{cc} u & z \\ y & X_1 \\ \end{array} \right) \end{align}\] ここで、\( u \) は \( \left( 1,1 \right) \) 成分です。また、\( X_1 \) は \( n - 1 \) 次行列、\( y \) は \( n - 1 \) 項列ベクトル、\( z \) は \( n - 1 \) 項行ベクトルです。 \[ \begin{align} \left( Q^{-1} X P^{-1} \right) \left( PAQ \right) = E \end{align}\] が成り立つため、 \[ \begin{align} \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & E_{n-1} \\ \end{array} \right) &= \left( \begin{array}{cc} u & z \\ y & X_1 \\ \end{array} \right) \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \\\\ &= \left( \begin{array}{cc} u & zA_{1} \\ y & X_1 A_1 \\ \end{array} \right) \end{align}\] よって、 \[ \begin{align} X_1 A_1 = E_{n-1} \end{align}\] が成り立ちます。この式と、帰納法の仮定より、\( A_1 \) は正則と言えます。 よって、対称区分けされた正方行列の正則性についての定理より、\( B \) も正則となります。 すると、\( A = P^{-1} B Q^{-1} \) であるので \( A \) も正則となります。
\( AX = E \) となる \( n \) 次行列 \( X \) が存在する場合は、 \[ \begin{align} \left( PAQ \right) \left( Q^{-1} X P^{-1} \right) = E \end{align}\] となることから、 \[ \begin{align} \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & E_{n-1} \\ \end{array} \right) &= \left( \begin{array}{cc} 1 & O_{1,n-1} \\ O_{n-1,1} & A_1 \\ \end{array} \right) \left( \begin{array}{cc} u & z \\ y & X_1 \\ \end{array} \right) \\\\ &= \left( \begin{array}{cc} u & z \\ A_1 y & A_1 X_1 \\ \end{array} \right) \end{align}\] が成り立ち、あとは \( XA = E \) となる \( n \) 次行列 \( X \) が存在する場合と同様の手順で証明できます。
階数
\[ 階数 \]
任意の \( \left( m, n \right) \) 型行列 \( A \) は、基本変形を何回か施すことにより、次の標準形 \( F_{m, \ n} \left( r \right) \)
に変形することができる。
\[ \begin{align}
F_{m, \ n} \left( r \right) &=
\left(
\begin{array}{cc}
E_{r} & O_{r, \ n-r} \\
O_{m-r, \ r} & O_{m-r, \ n-r}
\end{array}
\right)
\end{align}\]
ここで、\( r \) は \( A \) のみによって決まる数であり、これを行列 \( A \) の階数またはランクと呼ぶ。
上の定理を証明します。まずは、標準形 \( F_{m, \ n} \left( r \right) \) が構成できることを示します。
まず、\( A = O \) の場合は、\( A = F_{m, \ n} \left( 0 \right) \) とみなします。 次に、\( A \neq 0 \) の場合は、必要なら、行および列の交換を行い \( \left( 1,1 \right) \) 成分が 0 でなくなるように基本変形を施します。 そして、\( \left( 1,1 \right) \) をかなめとして、左右から第 1 列および第 1 行を掃出せば、 \[ \begin{align} \left( \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & & & \\ \vdots & & * & \\ 0 & & & \end{array} \right) \end{align}\] の形になります。この段階で、第 1 列および第 1 行以外(上の行列の*で示した部分)のすべての成分が 0 であれば、標準形 \( F_{m, \ n} \left( 1 \right) \) となります。 一方、*で示した部分に 0 でない成分があれば、それを \( \left( 2,2 \right) \) 成分に移して、 \( \left( 2,2 \right) \) をかなめとして左右から第 1 列および第 1 行を掃出します。すると、 \[ \begin{align} \left( \begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & & & \\ \vdots & \vdots & & * & \\ 0 & 0 & & & \end{array} \right) \end{align}\] となり、この段階で上の行列の*で示した部分のすべての成分が 0 であれば、標準形 \( F_{m, \ n} \left( 2 \right) \) となります。 もし、*で示した部分に 0 でない成分があれば、同様の操作を続けていけば、どこかの段階で標準形になります。 \( m \) と \( n \) のうち大きい方を \( L \) とおけば、この操作は最大でも \( L \) 回で終了して標準形になるため、 標準形 \( F_{m, \ n} \left( r \right) \) が構成できることが示せました。
次に、\( r \) が \( A \) のみによって決まることを示します。 仮に、\( A \) が二通りの標準形 \( F \left( r \right) = F_{m, \ n} \left( r \right) \) および \( F \left( s \right) = F_{m, \ n} \left( s \right) \) を持つとします。 ただし、\( r \leq s \) と仮定します。 \( F \left( r \right) \) と \( F \left( s \right) \) とは基本変形を組み合わせたものにより移りあえるため、 適当な \( m \) 次正則行列 \( P \) 、\( n \) 次正則行列 \( Q \) を用いて、 \[ \begin{align} F \left( s \right) = P F \left( r \right) Q \end{align}\] と表されます。
続いて、\( P \) 、\( Q \) の行と列を \( r \) 番目で区切って 4 つに対称に区分けして、 \[ \begin{align} P = \left( \begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array} \right) , \ Q = \left( \begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array} \right) \end{align}\] とすると、 \[ \begin{align} F \left( s \right) &= \left( \begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array} \right) \left( \begin{array}{cc} E_{r} & O_{r, \ n-r} \\ O_{m-r, \ r} & O_{m-r, \ n-r} \end{array} \right) \left( \begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array} \right) \\\\ &= \left( \begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array} \right) \left( \begin{array}{cc} Q_{11} & Q_{12} \\ O_{m-r, \ r} & O_{m-r, \ n-r} \end{array} \right) \\\\ &= \left( \begin{array}{cc} P_{11} Q_{11} & P_{11} Q_{12} \\ P_{21} Q_{11} & P_{21} Q_{12} \end{array} \right) \end{align}\] \( P \) 、\( Q \) の行と列は \( r \) 番目で区切ってあるため、 \[ \begin{align} P_{11} Q_{11} &= E_r \\\\ P_{11} Q_{12} &= O_{r, \ n-r} \\\\ P_{21} Q_{11} &= O_{m-r, \ r} \end{align}\] が成り立ちます。先ほど証明した左(右)逆行列の存在と正則性の定理より、 \( P_{11} Q_{11} = E_r \) から \( P_{11} \) と \( Q_{11} \) は正則であるといえます。 よって、\( P_{11} \neq O \) と \( Q_{11} \neq O \) 、 および \( P_{11} Q_{12} = O_{r, \ n-r} \) と \( P_{21} Q_{11} = O_{m-r, \ r} \) から、 \[ \begin{align} Q_{12} &= O_{r, \ n-r} \\\\ P_{21} &= O_{m-r, \ r} \end{align}\] が成り立ちます。よって、 \[ \begin{align} P_{21} Q_{12} = O_{m-r, \ n-r} \end{align}\] が成り立ち、これは \( r = s \) を意味するため、 二通りの標準形 \( F \left( r \right) \) と \( F \left( s \right) \) は同じものになります。 ゆえに、\( r \) が \( A \) のみによって決まるといえます。
まず、\( A = O \) の場合は、\( A = F_{m, \ n} \left( 0 \right) \) とみなします。 次に、\( A \neq 0 \) の場合は、必要なら、行および列の交換を行い \( \left( 1,1 \right) \) 成分が 0 でなくなるように基本変形を施します。 そして、\( \left( 1,1 \right) \) をかなめとして、左右から第 1 列および第 1 行を掃出せば、 \[ \begin{align} \left( \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & & & \\ \vdots & & * & \\ 0 & & & \end{array} \right) \end{align}\] の形になります。この段階で、第 1 列および第 1 行以外(上の行列の*で示した部分)のすべての成分が 0 であれば、標準形 \( F_{m, \ n} \left( 1 \right) \) となります。 一方、*で示した部分に 0 でない成分があれば、それを \( \left( 2,2 \right) \) 成分に移して、 \( \left( 2,2 \right) \) をかなめとして左右から第 1 列および第 1 行を掃出します。すると、 \[ \begin{align} \left( \begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & & & \\ \vdots & \vdots & & * & \\ 0 & 0 & & & \end{array} \right) \end{align}\] となり、この段階で上の行列の*で示した部分のすべての成分が 0 であれば、標準形 \( F_{m, \ n} \left( 2 \right) \) となります。 もし、*で示した部分に 0 でない成分があれば、同様の操作を続けていけば、どこかの段階で標準形になります。 \( m \) と \( n \) のうち大きい方を \( L \) とおけば、この操作は最大でも \( L \) 回で終了して標準形になるため、 標準形 \( F_{m, \ n} \left( r \right) \) が構成できることが示せました。
次に、\( r \) が \( A \) のみによって決まることを示します。 仮に、\( A \) が二通りの標準形 \( F \left( r \right) = F_{m, \ n} \left( r \right) \) および \( F \left( s \right) = F_{m, \ n} \left( s \right) \) を持つとします。 ただし、\( r \leq s \) と仮定します。 \( F \left( r \right) \) と \( F \left( s \right) \) とは基本変形を組み合わせたものにより移りあえるため、 適当な \( m \) 次正則行列 \( P \) 、\( n \) 次正則行列 \( Q \) を用いて、 \[ \begin{align} F \left( s \right) = P F \left( r \right) Q \end{align}\] と表されます。
続いて、\( P \) 、\( Q \) の行と列を \( r \) 番目で区切って 4 つに対称に区分けして、 \[ \begin{align} P = \left( \begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array} \right) , \ Q = \left( \begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array} \right) \end{align}\] とすると、 \[ \begin{align} F \left( s \right) &= \left( \begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array} \right) \left( \begin{array}{cc} E_{r} & O_{r, \ n-r} \\ O_{m-r, \ r} & O_{m-r, \ n-r} \end{array} \right) \left( \begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array} \right) \\\\ &= \left( \begin{array}{cc} P_{11} & P_{12} \\ P_{21} & P_{22} \end{array} \right) \left( \begin{array}{cc} Q_{11} & Q_{12} \\ O_{m-r, \ r} & O_{m-r, \ n-r} \end{array} \right) \\\\ &= \left( \begin{array}{cc} P_{11} Q_{11} & P_{11} Q_{12} \\ P_{21} Q_{11} & P_{21} Q_{12} \end{array} \right) \end{align}\] \( P \) 、\( Q \) の行と列は \( r \) 番目で区切ってあるため、 \[ \begin{align} P_{11} Q_{11} &= E_r \\\\ P_{11} Q_{12} &= O_{r, \ n-r} \\\\ P_{21} Q_{11} &= O_{m-r, \ r} \end{align}\] が成り立ちます。先ほど証明した左(右)逆行列の存在と正則性の定理より、 \( P_{11} Q_{11} = E_r \) から \( P_{11} \) と \( Q_{11} \) は正則であるといえます。 よって、\( P_{11} \neq O \) と \( Q_{11} \neq O \) 、 および \( P_{11} Q_{12} = O_{r, \ n-r} \) と \( P_{21} Q_{11} = O_{m-r, \ r} \) から、 \[ \begin{align} Q_{12} &= O_{r, \ n-r} \\\\ P_{21} &= O_{m-r, \ r} \end{align}\] が成り立ちます。よって、 \[ \begin{align} P_{21} Q_{12} = O_{m-r, \ n-r} \end{align}\] が成り立ち、これは \( r = s \) を意味するため、 二通りの標準形 \( F \left( r \right) \) と \( F \left( s \right) \) は同じものになります。 ゆえに、\( r \) が \( A \) のみによって決まるといえます。
階数と正則性の関係
\[ 階数および基本変形と正則性\]
(a) \( n \) 次正方行列 \( A \) が正則であるためには、その階数が \( n \) に等しいことが必要十分条件である。
(b) \( A \) が正則ならば、左基本変形あるいは右基本変形のみによって \( A \) を単位行列に変形することができる。逆もまた成り立つ。
(b) \( A \) が正則ならば、左基本変形あるいは右基本変形のみによって \( A \) を単位行列に変形することができる。逆もまた成り立つ。
まずは (a) を証明します。基本変形を何回か施して、\( A \) を次のように標準形へと変形できたとします。
\[ PAQ = F_{n, \ n} \left( r \right) \]
ここで、\( P \) と \( Q \) は正則行列とします。
\( A \) が正則ならば、\( PAQ \) も正則であるため、\( F_{n, \ n} \left( r \right) \) は正則となります。
よって、対角行列が正則であるための条件より \( r = n \) であることが導かれます。
逆に、\( r = n \) ならば、\( F_{n, \ n} \left( r \right) = E_n \) であるため、
\[ A = P^{-1} Q^{-1} \]
となり、\( A \) は正則であることがわかります。
続いて、(b) を証明します。\( A \) が正則なら、(a) より、\( P \) および \( Q \) を基本行列の積からなる正則行列として \[ PAQ = E \] が成り立ちます。この式の左から \( Q \) 、右から \( Q^{-1} \) をかければ、 \[ QPA = E \] となり、\( QP \) も基本行列の積であるため、左基本変形だけによって \( A \) を単位行列に変形できたことになります。 また、先ほどの式に右から \( P \) 、左から \( P^{-1} \) をかければ、 \[ AQP = E \] となり、右基本変形だけによって \( A \) を単位行列に変形できたことになります。
逆については、\( QPA = E \) が成り立つ場合、これに左から \( P^{-1} Q^{-1} \) をかければ、 \[ A = P^{-1} Q^{-1} \] となり、\( A \) は正則となります。同様に、\( AQP = E \) が成り立つ場合、これに右から \( P^{-1} Q^{-1} \) をかければ、 \[ A = P^{-1} Q^{-1} \] となり、\( A \) は正則となります。
続いて、(b) を証明します。\( A \) が正則なら、(a) より、\( P \) および \( Q \) を基本行列の積からなる正則行列として \[ PAQ = E \] が成り立ちます。この式の左から \( Q \) 、右から \( Q^{-1} \) をかければ、 \[ QPA = E \] となり、\( QP \) も基本行列の積であるため、左基本変形だけによって \( A \) を単位行列に変形できたことになります。 また、先ほどの式に右から \( P \) 、左から \( P^{-1} \) をかければ、 \[ AQP = E \] となり、右基本変形だけによって \( A \) を単位行列に変形できたことになります。
逆については、\( QPA = E \) が成り立つ場合、これに左から \( P^{-1} Q^{-1} \) をかければ、 \[ A = P^{-1} Q^{-1} \] となり、\( A \) は正則となります。同様に、\( AQP = E \) が成り立つ場合、これに右から \( P^{-1} Q^{-1} \) をかければ、 \[ A = P^{-1} Q^{-1} \] となり、\( A \) は正則となります。
参考:
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行