目次
・行列
・行列の和と定数倍
・行列の積
・追記:零行列
行列
\[ 行列\]
\( m \) 、\( n \) を任意の自然数とする。
\( m \times n \) 個の複素数
\[ \begin{align}
a_{ij} \ \ \ \left( i = 1,2, \ldots ,m \ ; \ \ j = 1,2, \ldots ,n \right)
\end{align}\]
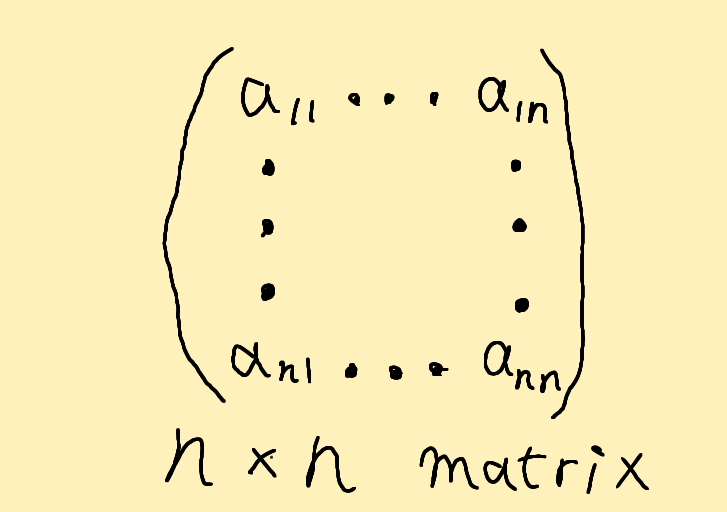
を、縦 \( m \) 個、横 \( n \) 個の長方形に並べたものを、\( \left( m, n \right) \) 型の行列と呼び、これを
\[ \begin{align}
A = \left( a_{ij} \right) = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1n} \\
a_{21} & a_{22} & \ldots & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
\right)
\end{align}\]
と表す。
\( \left( m, 1 \right) \) 型の行列を \( m \) 項列ベクトル、あるいは \( m \) 項縦ベクトルと呼びます。
また、\( \left( 1, n \right) \) 型の行列を \( n \) 項行ベクトル、あるいは \( n \) 項横ベクトルと呼びます。
行列を構成する \( m \times n \) 個の複素数を行列の成分と呼びます。 特に、上から \( i \) 番目、左から \( j \) 番目の位置にある成分 \( a_{ij} \) を \( \left( i, j \right) \) 成分と呼びます。 横に一列に並んだ列を行と呼び、縦に一列に並んだ列を列と呼びます。 特に、上から \( i \) 番目の行を第 \( i \) 行、左から \( j \) 番目の列を第 \( j \) 列と呼びます。
\( \left( m, n \right) \) 型の行列 \( A = \left( a_{ij} \right) \) の第 \( j \) 列だけを取り出したものを、行列 \( A \) の第 \( j \) 列ベクトルと呼びます。 これを用いて、 \[ \begin{align} \boldsymbol a_1 \ \mathrm = \left( \begin{array}{cccc} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right) , \ \boldsymbol a_2 \ \mathrm = \left( \begin{array}{cccc} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right) , \ \ldots \ , \ \boldsymbol a_n \ \mathrm = \left( \begin{array}{cccc} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{array} \right) \end{align}\] と表されるとき、 \[ \begin{align} A = \left( \boldsymbol a_1 \ \ \boldsymbol a_2 \ \ \cdots \ \ \boldsymbol a_n \right) \end{align}\] と書くことがあります。 行についても同様に \( A \) の第 \( i \) 行だけを取り出したものを、行列 \( A \) の第 \( i \) 行ベクトルと呼びます。 これを用いて、 \[ \begin{align} & \boldsymbol a_1 \ \mathrm = \left( a_{11} , a_{12} , \cdots , a_{1n} \right) \\\\ & \boldsymbol a_2 \ \mathrm = \left( a_{21} , a_{22} , \cdots , a_{2n} \right) \\\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\\\ & \boldsymbol a_m \ \mathrm = \left( a_{m1} , a_{m2} , \cdots , a_{mn} \right) \end{align}\] と表されるとき、 \[ \begin{align} A = \left( \begin{array}{c} \boldsymbol a_1 \\ \boldsymbol a_2 \\ \vdots \\ \boldsymbol a_m \end{array} \right) \end{align}\] と書くことがあります。
行列の成分は一般に複素数を取りますが、特に成分がすべて実数である行列は実行列と呼ばれます。
行列におけるイコールは次のように定義します。
行列を構成する \( m \times n \) 個の複素数を行列の成分と呼びます。 特に、上から \( i \) 番目、左から \( j \) 番目の位置にある成分 \( a_{ij} \) を \( \left( i, j \right) \) 成分と呼びます。 横に一列に並んだ列を行と呼び、縦に一列に並んだ列を列と呼びます。 特に、上から \( i \) 番目の行を第 \( i \) 行、左から \( j \) 番目の列を第 \( j \) 列と呼びます。
\( \left( m, n \right) \) 型の行列 \( A = \left( a_{ij} \right) \) の第 \( j \) 列だけを取り出したものを、行列 \( A \) の第 \( j \) 列ベクトルと呼びます。 これを用いて、 \[ \begin{align} \boldsymbol a_1 \ \mathrm = \left( \begin{array}{cccc} a_{11} \\ a_{21} \\ \vdots \\ a_{m1} \end{array} \right) , \ \boldsymbol a_2 \ \mathrm = \left( \begin{array}{cccc} a_{12} \\ a_{22} \\ \vdots \\ a_{m2} \end{array} \right) , \ \ldots \ , \ \boldsymbol a_n \ \mathrm = \left( \begin{array}{cccc} a_{1n} \\ a_{2n} \\ \vdots \\ a_{mn} \end{array} \right) \end{align}\] と表されるとき、 \[ \begin{align} A = \left( \boldsymbol a_1 \ \ \boldsymbol a_2 \ \ \cdots \ \ \boldsymbol a_n \right) \end{align}\] と書くことがあります。 行についても同様に \( A \) の第 \( i \) 行だけを取り出したものを、行列 \( A \) の第 \( i \) 行ベクトルと呼びます。 これを用いて、 \[ \begin{align} & \boldsymbol a_1 \ \mathrm = \left( a_{11} , a_{12} , \cdots , a_{1n} \right) \\\\ & \boldsymbol a_2 \ \mathrm = \left( a_{21} , a_{22} , \cdots , a_{2n} \right) \\\\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots \\\\ & \boldsymbol a_m \ \mathrm = \left( a_{m1} , a_{m2} , \cdots , a_{mn} \right) \end{align}\] と表されるとき、 \[ \begin{align} A = \left( \begin{array}{c} \boldsymbol a_1 \\ \boldsymbol a_2 \\ \vdots \\ \boldsymbol a_m \end{array} \right) \end{align}\] と書くことがあります。
行列の成分は一般に複素数を取りますが、特に成分がすべて実数である行列は実行列と呼ばれます。
行列におけるイコールは次のように定義します。
2つの行列 \( A \) と \( B \) が同じ型の行列であり、\( A \) と \( B \) の対応する成分がすべて等しいとき、\( A \) と \( B \)
は等しいといい、このことを \( A=B \) で表す。すなわち、
\[ \begin{align}
A = \left( a_{ij} \right) = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1n} \\
a_{21} & a_{22} & \ldots & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
\right)
\end{align}\]
\[ \begin{align}
B = \left( b_{ij} \right) = \left(
\begin{array}{cccc}
b_{11} & b_{12} & \ldots & b_{1n} \\
b_{21} & b_{22} & \ldots & b_{2n} \\
\vdots & \vdots & & \vdots \\
b_{m1} & b_{m2} & \ldots & b_{mn}
\end{array}
\right)
\end{align}\]
と表されているとき、
\[ \begin{align}
a_{ij} = b_{ij}\ \ \ \left( i = 1,2, \ldots ,m \ ; \ \ j = 1,2, \ldots ,n \right)
\end{align}\]
が成り立つことを、\( A=B \) で表す。
行列の和と定数倍
\[ 行列の和と定数倍\]
2つの \( \left( m, n \right) \) 型の行列 \( A \) 、\( B \) に対して、対応する成分の和を成分とする同じ型の行列を \( A \) と \( B \)
の和と呼び、\( A+B \) で表す。すなわち、
\[ \begin{align}
A = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1n} \\
a_{21} & a_{22} & \ldots & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
\right)
\end{align}\]
\[ \begin{align}
B = \left(
\begin{array}{cccc}
b_{11} & b_{12} & \ldots & b_{1n} \\
b_{21} & b_{22} & \ldots & b_{2n} \\
\vdots & \vdots & & \vdots \\
b_{m1} & b_{m2} & \ldots & b_{mn}
\end{array}
\right)
\end{align}\]
ならば、
\[ \begin{align}
A + B = \left(
\begin{array}{cccc}
a_{11} + b_{11} & a_{12} + b_{12} & \ldots & a_{1n} + b_{1n} \\
a_{21} + b_{21} & a_{22} + b_{22} & \ldots & a_{2n} + b_{2n} \\
\vdots & \vdots & & \vdots \\
a_{m1} + b_{m1} & a_{m2} + b_{m2} & \ldots & a_{mn} + b_{mn}
\end{array}
\right)
\end{align}\]
である。
また、複素数 \( c \) に対し、\( \left( m, n \right) \) 型の行列 \( A \) の各成分を \( c \) 倍して得られる同じ型の行列を、 \( A \) の \( c \) 倍と呼び、\( cA \) と表す。すなわち、 \[ \begin{align} cA = \left( \begin{array}{cccc} ca_{11} & ca_{12} & \ldots & ca_{1n} \\ ca_{21} & ca_{22} & \ldots & ca_{2n} \\ \vdots & \vdots & & \vdots \\ ca_{m1} & ca_{m2} & \ldots & ca_{mn} \end{array} \right) \end{align}\] である。特に、\( \left( -1 \right) A \) を \( -A \) で表す。 さらに、\( A + \left( - B \right) \) を \( A - B \) で表す。
また、複素数 \( c \) に対し、\( \left( m, n \right) \) 型の行列 \( A \) の各成分を \( c \) 倍して得られる同じ型の行列を、 \( A \) の \( c \) 倍と呼び、\( cA \) と表す。すなわち、 \[ \begin{align} cA = \left( \begin{array}{cccc} ca_{11} & ca_{12} & \ldots & ca_{1n} \\ ca_{21} & ca_{22} & \ldots & ca_{2n} \\ \vdots & \vdots & & \vdots \\ ca_{m1} & ca_{m2} & \ldots & ca_{mn} \end{array} \right) \end{align}\] である。特に、\( \left( -1 \right) A \) を \( -A \) で表す。 さらに、\( A + \left( - B \right) \) を \( A - B \) で表す。
和と定数倍については、次の演算法則が成り立ちます。
\[ 行列の和と定数倍の演算法則\]
\[ \begin{align}
\left( A + B \right) + C &= A + \left( B + C \right) \\\\
A + B &= B + A \\\\
c \left( A + B \right) &= cA + cB \\\\
\left( c + d \right) A &= cA + dA \\\\
\left( cd \right) A &= c \left( dA \right)
\end{align}\]
行列の積
\[ 行列の積\]
\( A \) を \( \left( l,m \right) \) 型行列、\( B \) を \( \left( m,n \right) \) 型行列とする。
\[ \begin{align}
A = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1m} \\
a_{21} & a_{22} & \ldots & a_{2m} \\
\vdots & \vdots & & \vdots \\
a_{l1} & a_{l2} & \ldots & a_{lm}
\end{array}
\right)
\end{align}\]
\[ \begin{align}
B = \left(
\begin{array}{cccc}
b_{11} & b_{12} & \ldots & b_{1n} \\
b_{21} & b_{22} & \ldots & b_{2n} \\
\vdots & \vdots & & \vdots \\
b_{m1} & b_{m2} & \ldots & b_{mn}
\end{array}
\right)
\end{align}\]
と表されているとき、積 \( AB \) を次式で定義する。
\[ \begin{align}
AB = \left(
\begin{array}{cccc}
\sum _{j = 1} ^m a_{1j} b_{j1} & \sum _{j = 1} ^m a_{1j} b_{j2} & \ldots & \sum _{j = 1} ^m a_{1j}
b_{jn} \\
\sum _{j = 1} ^m a_{2j} b_{j1} & \sum _{j = 1} ^m a_{2j} b_{j2} & \ldots & \sum _{j = 1} ^m a_{2j}
b_{jn} \\
\vdots & \vdots & & \vdots \\
\sum _{j = 1} ^m a_{lj} b_{j1} & \sum _{j = 1} ^m a_{lj} b_{j2} & \ldots & \sum _{j = 1} ^m a_{lj}
b_{jn}
\end{array}
\right)
\end{align}\]
行列の積は、行列の和と比べると少しわかりにくいかもしれません。
具体例を一つ挙げてみると、
\[ \begin{align}
A = \left(
\begin{array}{cccc}
1 & 2 & 3 \\
2 & 1 & 3 \\
\end{array}
\right)
, \
B = \left(
\begin{array}{cccc}
1 & 3 \\
2 & 2 \\
3 & 1 \\
\end{array}
\right)
\end{align}\]
とすれば、
\[ \begin{align}
AB &= \left(
\begin{array}{cccc}
1 \cdot 1 + 2 \cdot 2 + 3 \cdot 3 & 1 \cdot 3 + 2 \cdot 2 + 3 \cdot 1 \\
2 \cdot 1 + 1 \cdot 2 + 3 \cdot 3 & 2 \cdot 3 + 1 \cdot 2 + 3 \cdot 1 \\
\end{array}
\right) \\\\
&= \left(
\begin{array}{cccc}
14 & 10 \\
13 & 11 \\
\end{array}
\right)
\end{align}\]
となります。
\( A \) が \( \left( l,m \right) \) 型行列、\( B \) が \( \left( m,n \right) \) 型行列であって、\( B \) の列ベクトルを \[ \begin{align} \boldsymbol b_1 ,\ \ \boldsymbol b_2 ,\ \ \cdots \ ,\ \boldsymbol b_n \end{align}\] とすれば、 \( \left( l,n \right) \) 型行列 \( AB \) の列ベクトルは、 \[ \begin{align} A \boldsymbol b_1 ,\ A \boldsymbol b_2 ,\ \cdots \ ,\ A \boldsymbol b_n \end{align}\] となります。 そのため、 \[ \begin{align} AB = \left( A \boldsymbol b_1 \ \ A \boldsymbol b_2 \ \ \cdots \ \ A \boldsymbol b_n \right) \end{align}\] と表すことがあります。 また、\( A \) の行ベクトルを \[ \begin{align} \boldsymbol a_1 ,\ \ \boldsymbol a_2 ,\ \ \cdots \ ,\ \boldsymbol a_l \end{align}\] とすれば、\( AB \) の行ベクトルは、 \[ \begin{align} \boldsymbol a_1 B ,\ \boldsymbol a_2 B ,\ \cdots \ ,\ \boldsymbol a_l B \end{align}\] となります。そのため、 \[ \begin{align} AB = \left( \begin{array}{c} \boldsymbol a_1 B \\ \boldsymbol a_2 B \\ \vdots \\ \boldsymbol a_l B \end{array} \right) \end{align}\] と表すことがあります。
行列の積については、次の演算法則が成り立ちます。
\( A \) が \( \left( l,m \right) \) 型行列、\( B \) が \( \left( m,n \right) \) 型行列であって、\( B \) の列ベクトルを \[ \begin{align} \boldsymbol b_1 ,\ \ \boldsymbol b_2 ,\ \ \cdots \ ,\ \boldsymbol b_n \end{align}\] とすれば、 \( \left( l,n \right) \) 型行列 \( AB \) の列ベクトルは、 \[ \begin{align} A \boldsymbol b_1 ,\ A \boldsymbol b_2 ,\ \cdots \ ,\ A \boldsymbol b_n \end{align}\] となります。 そのため、 \[ \begin{align} AB = \left( A \boldsymbol b_1 \ \ A \boldsymbol b_2 \ \ \cdots \ \ A \boldsymbol b_n \right) \end{align}\] と表すことがあります。 また、\( A \) の行ベクトルを \[ \begin{align} \boldsymbol a_1 ,\ \ \boldsymbol a_2 ,\ \ \cdots \ ,\ \boldsymbol a_l \end{align}\] とすれば、\( AB \) の行ベクトルは、 \[ \begin{align} \boldsymbol a_1 B ,\ \boldsymbol a_2 B ,\ \cdots \ ,\ \boldsymbol a_l B \end{align}\] となります。そのため、 \[ \begin{align} AB = \left( \begin{array}{c} \boldsymbol a_1 B \\ \boldsymbol a_2 B \\ \vdots \\ \boldsymbol a_l B \end{array} \right) \end{align}\] と表すことがあります。
行列の積については、次の演算法則が成り立ちます。
\[ 行列の積の演算法則\]
\[ \begin{align}
\left( A B \right) C &= A \left( B C \right) \\\\
A \left( B + C \right) &= AB + AC \\\\
\left( A + B \right) C &= AC + BC \\\\
c \left( AB \right) &= \left( cA \right) B = A \left( cB \right)
\end{align}\]
追記:零行列
\[ \begin{align}
零行列
\end{align}\]
成分がすべて 0 であるような \( \left( m , n \right) \) 型行列を \( \left( m , n \right) \) 型零行列と呼び、\( O_{m , \ n}
\) と表す。
単に \( O \) と表すこともある。
任意の \( \left( m , n \right) \) 型行列 \( A \) に対して、次が成り立つ。 \[ \begin{align} & A + O = A , \ A - A = O , \ 0A = O \\\\ & AO = O , \ OA = O \end{align}\]
任意の \( \left( m , n \right) \) 型行列 \( A \) に対して、次が成り立つ。 \[ \begin{align} & A + O = A , \ A - A = O , \ 0A = O \\\\ & AO = O , \ OA = O \end{align}\]
参考:
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行