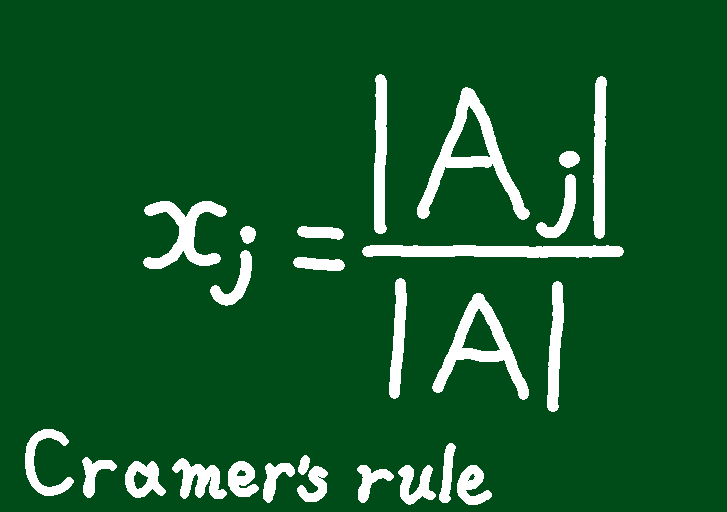
目次
・連立1次方程式
・クラメルの公式
・解の個数
連立1次方程式
\[ \rm 連立1次方程式\]
1次方程式のみからなる連立方程式のこと。一般に、\( n \) 個の未知数 \( x_1 , x_2 , \ldots , x_n \) についての \( n \) 個の1次方程式
\[ \begin{align}
a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n &= b_1 \\\\
a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n &= b_2 \\\\
\ \ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \\\\
a_{n1} x_1 + a_{n2} x_2 + \cdots + a_{nn} x_n &= b_n \\\\
\end{align}\]
からなる連立1次方程式を \( n \) 元連立1次方程式と呼ぶ。
\( n \) 次行列 \( A \) および \( n \) 項列ベクトル \( \boldsymbol x \) 、\( \boldsymbol b \) を
\[ \begin{align}
A = \left(
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1n} \\
a_{21} & a_{22} & \ldots & a_{2n} \\
\vdots & \vdots & & \vdots \\
a_{n1} & a_{n2} & \ldots & a_{nn}
\end{array}
\right) , \
\boldsymbol x = \left(
\begin{array}{cccc}
x_{1} \\
x_{2} \\
\vdots \\
x_{n}
\end{array}
\right) , \
\boldsymbol b = \left(
\begin{array}{cccc}
b_{1} \\
b_{2} \\
\vdots \\
b_{n}
\end{array}
\right)
\end{align}\]
とすれば、上の \( n \) 元連立1次方程式は、
\[ \begin{align}
A \boldsymbol x = \boldsymbol b \ \ \ldots \left( 1 \right)
\end{align}\]
と表せます。このとき、\( A \) を上の \( n \) 元連立1次方程式の係数行列と呼びます。
クラメルの公式
行列 \( A \) が正則であるなら、\( \left( 1 \right) \) 式の両辺に右から逆行列 \( A^{-1} \) をかけることにより、
\[ \begin{align}
\boldsymbol x &= A^{-1} \boldsymbol b \\\\
&= \frac{1}{\left| A \right|} \tilde{A} \boldsymbol b \\\\
&= \frac{1}{\left| A \right|}
\left(
\begin{array}{cccc}
\tilde{a}_{11} & \tilde{a}_{21} & \ldots & \tilde{a}_{n1} \\
\tilde{a}_{12} & \tilde{a}_{22} & \ldots & \tilde{a}_{n2} \\
\vdots & \vdots & & \vdots \\
\tilde{a}_{1n} & \tilde{a}_{2n} & \ldots & \tilde{a}_{nn}
\end{array}
\right)
\left(
\begin{array}{cccc}
b_{1} \\
b_{2} \\
\vdots \\
b_{n}
\end{array}
\right) \\\\
&= \frac{1}{\left| A \right|}
\left(
\begin{array}{cccc}
b_1 \tilde{a}_{11} + b_2 \tilde{a}_{21} + \ldots + b_n \tilde{a}_{n1} \\
b_1 \tilde{a}_{12} + b_2 \tilde{a}_{22} + \ldots + b_n \tilde{a}_{n2} \\
\vdots \\
b_1 \tilde{a}_{1n} + b_2 \tilde{a}_{2n} + \ldots + b_n \tilde{a}_{nn}
\end{array}
\right)
\end{align}\]
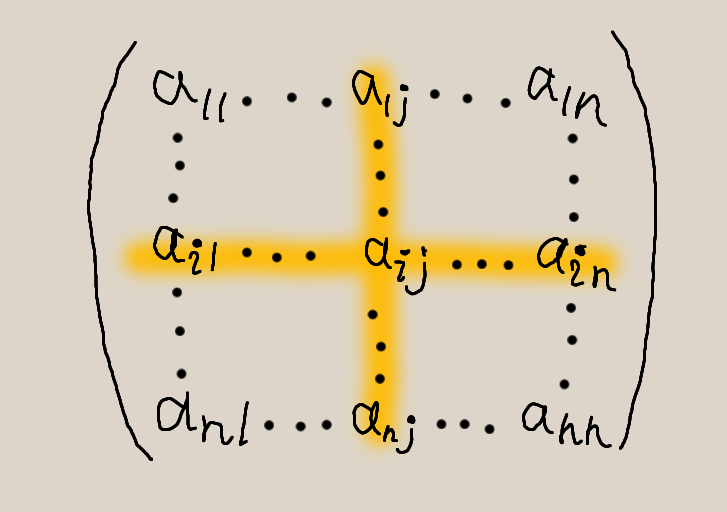
となります。上の式最終行の列ベクトルの第 \( j \) 成分は行列 \( A \) の第 \( j \) 列を \( \boldsymbol b \) で置き換えた行列
\[ \begin{align}
A_j =
\left(
\begin{array}{cccc}
a_{11} & \ldots & a_{1,j-1} & b_1 & a_{1,j+1} & \ldots & a_{n1} \\
a_{12} & \ldots & a_{2,j-1} & b_2 & a_{2,j+1} & \ldots & a_{n2} \\
\vdots & & \vdots & \vdots & \vdots & & \vdots \\
a_{1n} & \ldots & a_{n,j-1} & b_n & a_{n,j+1} & \ldots & a_{nn}
\end{array}
\right)
\end{align}\]
の第 \( j \) 列に関する展開式になります。よって、次の公式が成り立ちます。
\[ クラメルの公式\]
\( A \) を \( n \) 次正則行列、\( \boldsymbol x \) を未知の \( n \) 項列ベクトル、\( \boldsymbol b \) を \( n \) 項列ベクトルとする。
\( n \) 元連立1次方程式
\[ \begin{align}
A \boldsymbol x = \boldsymbol b
\end{align}\]
のただ一つの解は次式で与えられる。
\[ \begin{align}
x_j &= \frac{\left| A_j \right|}{\left| A \right|} \ \ \left( j = 1,2, \ldots , n \right)
\end{align}\]
ただし、\( A_j \) は行列 \( A \) の第 \( j \) 列を \( \boldsymbol b \) で置き換えた行列である。
これをクラメルの公式と呼ぶ。
解の個数
クラメルの公式より、\( n \) 元連立1次方程式
\[ \begin{align}
A \boldsymbol x = \boldsymbol b
\end{align}\]
の解の個数について、次のようにまとめられます。
[1] \( \left| A \right| \neq 0 \) かつ、 \( \boldsymbol b \) の成分のうち少なくとも 1 つは 0 でないならば、少なくとも 1 つの \( x_j \)
が 0 でない一意な解がある。
[2] \( \left| A \right| \neq 0 \) かつ、 \( \boldsymbol b \) の成分がすべて 0 ならば、 \[ \begin{align} x_1 = x_2 = \cdots = x_n = 0 \end{align}\] のみが解である。この解を自明な解と呼ぶ。
[2] \( \left| A \right| \neq 0 \) かつ、 \( \boldsymbol b \) の成分がすべて 0 ならば、 \[ \begin{align} x_1 = x_2 = \cdots = x_n = 0 \end{align}\] のみが解である。この解を自明な解と呼ぶ。
まずは、[1] を証明します。\( \boldsymbol b \) の成分のうち 0 でない成分を \( b_i \) とし、それ以外の成分をすべて 0 と仮定します。
すると、
\[ \begin{align}
x_j = \frac{b_i a_{ij}}{\left| A \right|} \ \ \left( j = 1,2, \ldots , n \right)
\end{align}\]
となります。もし、すべての \( j \) について \( x_j = 0 \) が成り立つならば、上の式より、すべての \( j \) について \( a_{ij} = 0 \) が成り立ちます。
すると、行列 \( A \) の第 \( i \) 行の成分はすべて 0 となりますが、これは \( \left| A \right| \neq 0 \) に反します。
よって、\( x_j \) のうち少なくとも 1 つは 0 でなく、また、クラメルの公式から解は一意に定まるとわかります。
[2] については条件より、任意の \( j \) について \( \left| A_j \right| = 0 \) が成り立ちます。 ゆえに、クラメルの公式より任意の \( j \) について \( x_j = 0 \) とわかります。
[2] については条件より、任意の \( j \) について \( \left| A_j \right| = 0 \) が成り立ちます。 ゆえに、クラメルの公式より任意の \( j \) について \( x_j = 0 \) とわかります。
参考:
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行
[2] 和達三樹、物理のための数学 (物理入門コース10)、岩波書店、1983年3月14日発行