目次
・置換
・互換
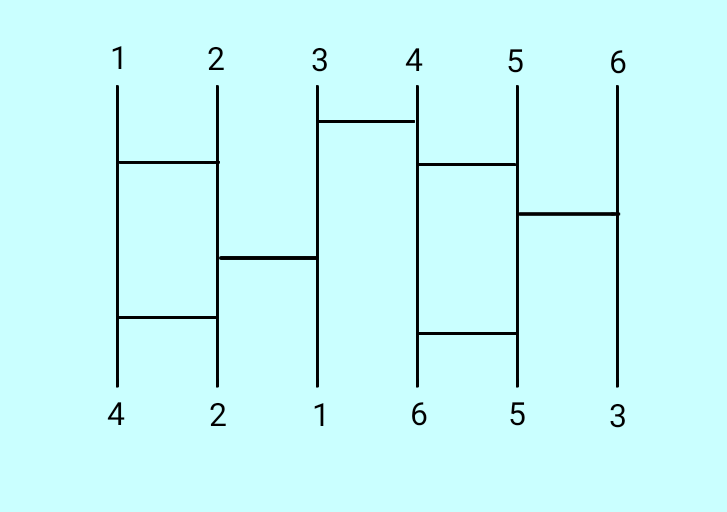
置換
\( 1,2, \ldots , n \) を並べ替える操作を置換と呼びます。
順列の総数の公式より、\( n \) 文字の置換は全部で \( n! \) 個あることがわかります。
置換は次にあげる方法で表記されます。
\[ 置換の表記\]
\( n \) 文字の置換 \( \sigma \) によって、\( i \) 番目の文字が \( j \) 番目に移されるとき、これを
\[ \begin{align}
\sigma \left( i \right) = j
\end{align}\]
と表す。また、
\[ \begin{align}
\sigma \left( 1 \right) = i_1 , \ \ \sigma \left( 2 \right) = i_2 , \ \ldots \ , \ \ \sigma \left( n
\right) = i_n
\end{align}\]
であるとき、
\[ \begin{align}
\sigma = \left(
\begin{array}{cccc}
1 & 2 & \ldots & n \\
i_1 & i_2 & \ldots & i_n \\
\end{array}
\right)
\end{align}\]
と表す。
\( n \) 文字の置換の特別な例として、恒等置換または単位置換と呼ばれるものがあります。
これは \( 1_n \) と表され、
\[ \begin{align}
1_n = \left(
\begin{array}{cccc}
1 & 2 & \ldots & n \\
1 & 2 & \ldots & n \\
\end{array}
\right)
\end{align}\]
となります。
\( n \) 文字の置換 \( \sigma \) の逆操作を \( \sigma \) の逆置換と呼び、\( \sigma ^{-1}\) で表します。 すなわち、 \[ \begin{align} \sigma = \left( \begin{array}{cccc} 1 & 2 & \ldots & n \\ i_1 & i_2 & \ldots & i_n \\ \end{array} \right) \end{align}\] ならば、 \[ \begin{align} \sigma ^{-1} = \left( \begin{array}{cccc} i_1 & i_2 & \ldots & i_n \\ 1 & 2 & \ldots & n \\ \end{array} \right) \end{align}\] となります。
置換には次に示す積と呼ばれる演算が定義されます。
\( n \) 文字の置換 \( \sigma \) の逆操作を \( \sigma \) の逆置換と呼び、\( \sigma ^{-1}\) で表します。 すなわち、 \[ \begin{align} \sigma = \left( \begin{array}{cccc} 1 & 2 & \ldots & n \\ i_1 & i_2 & \ldots & i_n \\ \end{array} \right) \end{align}\] ならば、 \[ \begin{align} \sigma ^{-1} = \left( \begin{array}{cccc} i_1 & i_2 & \ldots & i_n \\ 1 & 2 & \ldots & n \\ \end{array} \right) \end{align}\] となります。
置換には次に示す積と呼ばれる演算が定義されます。
\[ 置換の積\]
2 つの置換 \( \sigma \) と \( \tau \) を続けて行う操作を \( \sigma \) 、\( \tau \) の積と呼び、\( \tau \sigma \)
と表す。すなわち、
\[ \begin{align}
\sigma = \left(
\begin{array}{cccc}
1 & 2 & \ldots & n \\
i_1 & i_2 & \ldots & i_n \\
\end{array}
\right) , \ \ \
\tau = \left(
\begin{array}{cccc}
i_1 & i_2 & \ldots & i_n \\
j_1 & j_2 & \ldots & j_n \\
\end{array}
\right)
\end{align}\]
ならば、
\[ \begin{align}
\tau \sigma = \left(
\begin{array}{cccc}
1 & 2 & \ldots & n \\
j_1 & j_2 & \ldots & j_n \\
\end{array}
\right)
\end{align}\]
である。
\( \sigma \) 、\( \tau \) 、\( \rho \) を \( n \) 文字の置換とすると、置換の積の定義から、次の 3 つの性質が成り立ちます。
\[ \begin{align}
\left( \sigma \tau \right) \rho &= \sigma \left( \tau \rho \right) \\\\
1_n \sigma &= \sigma 1_n \\\\
\sigma \sigma ^{-1} &= \sigma ^{-1} \sigma = 1_n
\end{align}\]
\( n \) 文字の置換全体の集合を \( S_n \) で表すと、これについて次の定理が成り立ちます。
i) \( \sigma \) が \( S_n \) 全体を重複なく動くとき、\( \sigma ^{-1} \) も \( S_n \) 全体を重複なく動く。
ii) \( \tau \) を固定された一つの \( n \) 文字の置換とする。\( \sigma \) が \( S_n \) 全体を重複なく動くとき、\( \sigma \tau \) および \( \tau \sigma \) も \( S_n \) 全体を重複なく動く。
ii) \( \tau \) を固定された一つの \( n \) 文字の置換とする。\( \sigma \) が \( S_n \) 全体を重複なく動くとき、\( \sigma \tau \) および \( \tau \sigma \) も \( S_n \) 全体を重複なく動く。
i については、
\[ \begin{align}
\sigma _1 \neq \sigma _2 \rm \ \ \ ならば \ \ \ \it \sigma \rm _1 ^{-1} \neq \it \sigma \rm _2 ^{-1}
\end{align}\]
であることから、\( \sigma ^{-1} \) が重複しないために成り立ちます。
ii についても同様に、
\[ \begin{align}
\sigma _1 \neq \sigma _2 \rm \ \ \ ならば \ \ \ \it \sigma \rm _1 \it \tau \rm \neq \it \sigma \rm _2 \it \tau
\end{align}\]
\[ \begin{align}
\sigma _1 \neq \sigma _2 \rm \ \ \ ならば \ \ \ \it \tau \sigma \rm _1 \rm \neq \it \tau \sigma \rm _2
\end{align}\]
であることから、\( \sigma \tau \) および \( \tau \sigma \) が重複しないために成り立ちます。
互換
\( n \) 文字の置換で、2 つの文字のみを並べ替えるものを互換と呼びます。
任意の置換は互換の積で表すことができますが、その表し方は 1 通りではありません。
ですが、これについて次の定理が成り立ちます。
\[ 互換の積に関する定理\]
\( n \) 文字の置換 \( \sigma \) を互換の積として表す表し方は幾通りもあるが、
その際の互換の個数が偶数であるか奇数であるかどうかは、\( \sigma \) によって決まり、互換の積として表す表し方にはよらない。
上の定理を証明するにあたり、\( n \) 変数の差積と呼ばれる \( n \) 個の変数 \( x_1 , x_2 , \ldots , x_n \) からなる次の多項式 \( \Delta
\left( x_1 , x_2 , \ldots , x_n \right) \) を考えます。
\[ \begin{align}
\Delta \left( x_1 , x_2 , \ldots , x_n \right) &= \prod _{i \lt j} \left( x_j - x_i \right) \\\\
&= \prod _{j=2} ^n \left\{ \prod _{i=1} ^{j-1} \left( x_j - x_i \right) \right\} \\\\
&= \left( x_n - x_{n-1} \right) \left( x_n - x_{n-2} \right) \cdots \left( x_n - x_{2} \right) \left(
x_n - x_{1} \right) \times \\\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( x_{n-1} - x_{n-2} \right) \cdots \left( x_{n-1} - x_{2}
\right) \left( x_{n-1} - x_{1} \right) \times \\\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \cdots \cdots \cdots \\\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
\ \ \ \ \ \ \ \ \ \left( x_{3} - x_{2} \right) \left( x_{3} - x_{1} \right) \times \\\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( x_{2} - x_{1} \right)
\end{align}\]
なお、ここで
\[ \begin{align}
\prod _{i \lt j} \left( x_j - x_i \right)
\end{align}\]
は \( i \lt j \) を満たすあらゆる添え字の組 \( i,j \) にわたる \( \left( x_j - x_i \right) \) の積を表します。また、一般に数列 \( \left\{ a_k
\right\} \) について
\[ \begin{align}
\prod _{k=n} ^{m} a_k = a_n a_{n+1} \cdots a_{m}
\end{align}\]
と表します。
\( n \) 文字の置換 \( \sigma \) について、差積の定義より、 \[ \begin{align} \Delta \left( x_{\sigma \left( 1 \right)} , x_{\sigma \left( 2 \right)} , \ldots , x_{\sigma \left( n \right)} \right) = \pm \Delta \left( x_1 , x_2 , \ldots , x_n \right) \end{align}\] となることがわかります。もし、\( \tau \) が互換なら、 \[ \begin{align} \Delta \left( x_{\tau \left( 1 \right)} , x_{\tau \left( 2 \right)} , \ldots , x_{\tau \left( n \right)} \right) = - \Delta \left( x_1 , x_2 , \ldots , x_n \right) \end{align}\] となります。これについては、次のように考えます。
\( n \) 文字の置換 \( \sigma \) について、差積の定義より、 \[ \begin{align} \Delta \left( x_{\sigma \left( 1 \right)} , x_{\sigma \left( 2 \right)} , \ldots , x_{\sigma \left( n \right)} \right) = \pm \Delta \left( x_1 , x_2 , \ldots , x_n \right) \end{align}\] となることがわかります。もし、\( \tau \) が互換なら、 \[ \begin{align} \Delta \left( x_{\tau \left( 1 \right)} , x_{\tau \left( 2 \right)} , \ldots , x_{\tau \left( n \right)} \right) = - \Delta \left( x_1 , x_2 , \ldots , x_n \right) \end{align}\] となります。これについては、次のように考えます。
互換 \( \tau \) により交換する文字 \( i \) および \( j \) を、\( i \gt j \) となるように取る。
\( \Delta \left( x_1 , x_2 , \ldots , x_n \right) \) と \( \Delta \left( x_{\tau \left( 1 \right)} ,
x_{\tau \left( 2 \right)} , \ldots , x_{\tau \left( n \right)} \right) \) の違いを考えると、
互換 \( \tau \) により、\( x_i \) は \( x_j \) となり、\( x_j \) は \( x_i \) となる。
このとき、\( \left( x_i - x_j \right) \) は \( \left( x_j - x_i \right) \) になるため、マイナスの符号が 1 つ追加されることになる。
次に、文字 \( k \) について、3 通りに場合分けして考える。
[1] \( k \gt i \) の場合
差積に含まれる \( x_k \) と \( x_i \) からなる因数は \( \left( x_k - x_i \right) \) であり、\( x_k \) と \( x_j \) からなる因数は \( \left( x_k - x_j \right) \) である。 よって、 \( x_i \) と \( x_j \) を交換しても、これらの因数の式の形は変わらない。
[2] \( j \lt k \lt i \) の場合
差積に含まれる \( x_k \) と \( x_i \) からなる因数は \( \left( x_i - x_k \right) \) であり、\( x_k \) と \( x_j \) からなる因数は \( \left( x_k - x_j \right) \) である。 よって、 \( x_i \) と \( x_j \) を交換すると、これらの因数はいずれも \( -1 \) をかけた形になるが、2 つの \( -1 \) の積は \( 1 \) となるので、全体として式の形は変わらない。
[3] \( k \lt j \) の場合
差積に含まれる \( x_k \) と \( x_i \) からなる因数は \( \left( x_i - x_k \right) \) であり、\( x_k \) と \( x_j \) からなる因数は \( \left( x_j - x_k \right) \) である。 よって、 \( x_i \) と \( x_j \) を交換しても、これらの因数の式の形は変わらない。
[1] [2] [3] より、\( \left( x_i - x_j \right) \) 以外の因数は互換による差積の変化に影響を与えない。 したがって、互換による差積の変化はマイナスの符号が 1 つ追加されるだけとなり、 \[ \begin{align} \Delta \left( x_{\tau \left( 1 \right)} , x_{\tau \left( 2 \right)} , \ldots , x_{\tau \left( n \right)} \right) = - \Delta \left( x_1 , x_2 , \ldots , x_n \right) \end{align}\] が成り立つ。
[1] \( k \gt i \) の場合
差積に含まれる \( x_k \) と \( x_i \) からなる因数は \( \left( x_k - x_i \right) \) であり、\( x_k \) と \( x_j \) からなる因数は \( \left( x_k - x_j \right) \) である。 よって、 \( x_i \) と \( x_j \) を交換しても、これらの因数の式の形は変わらない。
[2] \( j \lt k \lt i \) の場合
差積に含まれる \( x_k \) と \( x_i \) からなる因数は \( \left( x_i - x_k \right) \) であり、\( x_k \) と \( x_j \) からなる因数は \( \left( x_k - x_j \right) \) である。 よって、 \( x_i \) と \( x_j \) を交換すると、これらの因数はいずれも \( -1 \) をかけた形になるが、2 つの \( -1 \) の積は \( 1 \) となるので、全体として式の形は変わらない。
[3] \( k \lt j \) の場合
差積に含まれる \( x_k \) と \( x_i \) からなる因数は \( \left( x_i - x_k \right) \) であり、\( x_k \) と \( x_j \) からなる因数は \( \left( x_j - x_k \right) \) である。 よって、 \( x_i \) と \( x_j \) を交換しても、これらの因数の式の形は変わらない。
[1] [2] [3] より、\( \left( x_i - x_j \right) \) 以外の因数は互換による差積の変化に影響を与えない。 したがって、互換による差積の変化はマイナスの符号が 1 つ追加されるだけとなり、 \[ \begin{align} \Delta \left( x_{\tau \left( 1 \right)} , x_{\tau \left( 2 \right)} , \ldots , x_{\tau \left( n \right)} \right) = - \Delta \left( x_1 , x_2 , \ldots , x_n \right) \end{align}\] が成り立つ。
では、ここで置換 \( \sigma \) が互換の積として 2 通りに表されているとします。
\[ \begin{align}
\sigma = \mu _1 \mu _2 \cdots \mu _k = \nu _1 \nu _2 \cdots \nu _l
\end{align}\]
すると、差積と互換の性質より、次式が成り立ちます。
\[ \begin{align}
\Delta \left( x_{\sigma \left( 1 \right)} , x_{\sigma \left( 2 \right)} , \ldots , x_{\sigma \left( n
\right)} \right) &= \left( -1 \right) ^k \Delta \left( x_1 , x_2 , \ldots , x_n \right) \\\\
&= \left( -1 \right) ^l \Delta \left( x_1 , x_2 , \ldots , x_n \right)
\end{align}\]
従って、\( \left( -1 \right) ^l = \left( -1 \right) ^k \) が成り立つため、\( k \) と \( l \) の偶奇性は一致することがわかります。
置換 \( \sigma \) が偶数個の互換の積であるとき偶置換、奇数個の互換の積であるとき奇置換と呼びます。 また、記号 \( \rm sgn \ \it \sigma \) を置換 \( \sigma \) の符号と呼び、\( \sigma \) が偶置換のときは \( \rm sgn \ \it \sigma \rm = 1 \) 、奇置換のときは \( \rm sgn \ \it \sigma \rm = -1 \) とします。 置換の符号について、次の性質が成り立ちます。 \[ \begin{align} \rm sgn \ 1 \it _n \rm &= 1 \\\\ \rm sgn \ \it \sigma \rm ^{-1} &= \rm sgn \ \it \sigma \\\\ \rm sgn \ \it \sigma \tau &= \rm sgn \ \it \sigma \cdot \rm sgn \ \it \tau \end{align}\]
置換 \( \sigma \) が偶数個の互換の積であるとき偶置換、奇数個の互換の積であるとき奇置換と呼びます。 また、記号 \( \rm sgn \ \it \sigma \) を置換 \( \sigma \) の符号と呼び、\( \sigma \) が偶置換のときは \( \rm sgn \ \it \sigma \rm = 1 \) 、奇置換のときは \( \rm sgn \ \it \sigma \rm = -1 \) とします。 置換の符号について、次の性質が成り立ちます。 \[ \begin{align} \rm sgn \ 1 \it _n \rm &= 1 \\\\ \rm sgn \ \it \sigma \rm ^{-1} &= \rm sgn \ \it \sigma \\\\ \rm sgn \ \it \sigma \tau &= \rm sgn \ \it \sigma \cdot \rm sgn \ \it \tau \end{align}\]
参考:
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行