第32話  内積・ノルム

この記事を読む助けになる数学の記事
・数値計算：1話、 5話、 26話、 30話

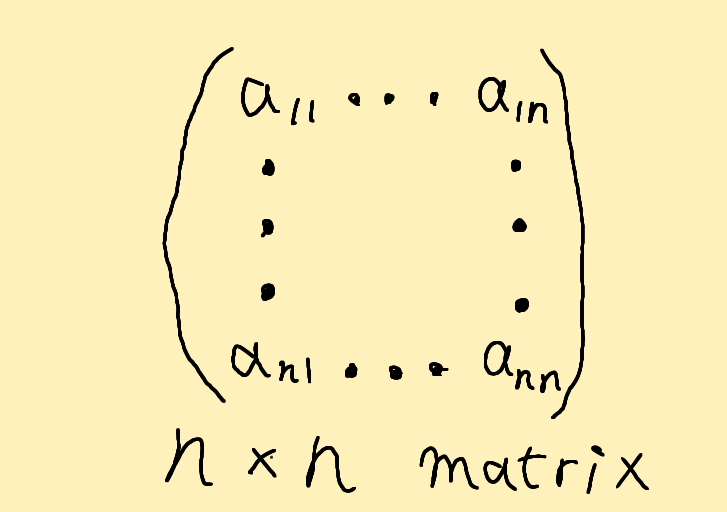
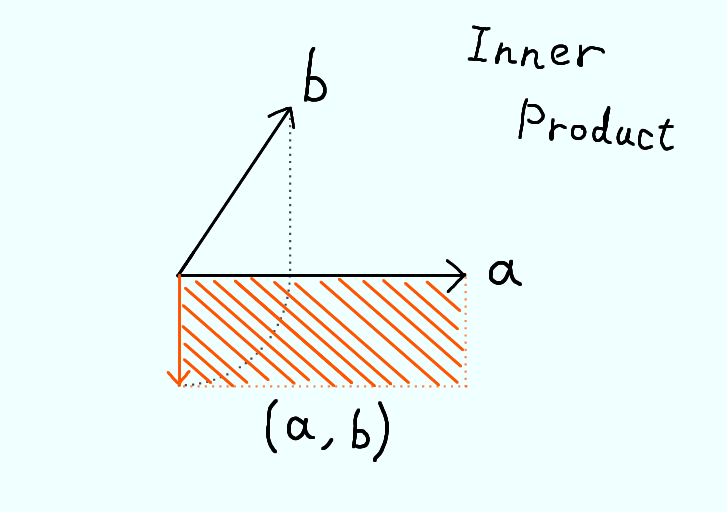
　内積について、共軛線型性と呼ばれる次の性質が成り立ちます。

　また、同一の \( n \) 項列ベクトル同士の内積 \( \left( \boldsymbol x , \boldsymbol x \right) \) は 0 または正の実数であり、 \[ \left( \boldsymbol x , \boldsymbol x \right) = 0 \] となるのは、\( \boldsymbol x \) の成分がすべて 0 である場合に限ります。 これは、内積の正値性と呼ばれています。

　さらに、\( \left( \boldsymbol x , \boldsymbol y \right) = 0 \) のとき、\( \boldsymbol x \) と \( \boldsymbol y \) は直交するといいます。

　ノルムについて、次の二つの不等式が成り立ちます。

　この二つの不等式を証明するために、まずは準備として次の定理を証明します。

　ピタゴラスの定理の証明は次の式変形によります。 \[ \begin{align} \| \boldsymbol{x} + \boldsymbol{y} \| ^2 &= \left( \boldsymbol x + \boldsymbol y, \boldsymbol x + \boldsymbol y \right) \\\\ &= \left( \boldsymbol x , \boldsymbol x + \boldsymbol y \right) + \left( \boldsymbol y, \boldsymbol x + \boldsymbol y \right) \\\\ &= \left( \boldsymbol x , \boldsymbol x \right) + \left( \boldsymbol x , \boldsymbol y \right) + \left( \boldsymbol y, \boldsymbol x \right) + \left( \boldsymbol y, \boldsymbol y \right) \\\\ &= \| \boldsymbol{x} \| ^2 + \left( \boldsymbol x , \boldsymbol y \right) + \left( \boldsymbol x, \boldsymbol y \right) ^* + \| \boldsymbol{y} \| ^2 \\\\ &= \| \boldsymbol{x} \| ^2 + \rm 2 Re \left( \it \boldsymbol x , \boldsymbol y \rm \right) + \| \it \boldsymbol{y} \rm \| ^2 \end{align}\] ここで、直交条件より \( \left( \boldsymbol x , \boldsymbol y \right) = 0 \) であるため、ピタゴラスの定理が成り立ちます。

　続いて、シュヴァルツの不等式を証明します。 \( \boldsymbol x \) の成分がすべて 0 である場合、シュヴァルツの不等式の両辺は 0 となるため、この不等式は成り立ちます。 そこで、\( \boldsymbol x \) の成分がすべて 0 でない場合、つまり \( \| \boldsymbol{x} \| \neq 0 \) である場合について考えます。 まずは、\( \boldsymbol y \) を次の 2 つの \( n \) 項列ベクトルに分解します。 \[ \begin{align} \boldsymbol y_1 &= \boldsymbol y - \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \| ^2} \\\\ \boldsymbol y_2 &= \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \| ^2} \end{align}\] 以下の計算から、\( \boldsymbol y_1 \) と \( \boldsymbol y_2 \) は直交することがわかります。 \[ \begin{align} \left( \boldsymbol y_1 , \boldsymbol y_2 \right) &= \left( \boldsymbol y - \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \|^2} , \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \|^2} \right) \\\\ &= \left( \boldsymbol y , \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \|^2} \right) - \left( \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \|^2}, \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \|^2} \right) \\\\ &= \frac{\left( \boldsymbol x , \boldsymbol y \right) }{\| \boldsymbol{x} \|^2} \left( \boldsymbol y , \boldsymbol x \right) - \frac{\left( \boldsymbol y , \boldsymbol x \right) }{\| \boldsymbol{x} \|^2} \left( \boldsymbol x, \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \|^2} \right) \\\\ &= \frac{\left( \boldsymbol x , \boldsymbol y \right) }{\| \boldsymbol{x} \|^2} \left( \boldsymbol y , \boldsymbol x \right) - \frac{\left( \boldsymbol y , \boldsymbol x \right) }{\| \boldsymbol{x} \|^2} \frac{\left( \boldsymbol x , \boldsymbol y \right) }{\| \boldsymbol{x} \|^2} \left( \boldsymbol x, \boldsymbol x \right) \\\\ &= \frac{\left( \boldsymbol x , \boldsymbol y \right) }{\| \boldsymbol{x} \|^2} \left( \boldsymbol y , \boldsymbol x \right) - \frac{\left( \boldsymbol y , \boldsymbol x \right) }{\| \boldsymbol{x} \|^2} \left( \boldsymbol x , \boldsymbol y \right) = 0 \end{align}\] よって、ピタゴラスの定理より、 \[ \begin{align} \| \boldsymbol{y} \|^2 &= \| \boldsymbol{y} _1 + \boldsymbol{y} _2 \|^2 \\\\ &= \| \boldsymbol{y} _1 \|^2 + \| \boldsymbol{y} _2 \|^2 \\\\ & \geq \| \boldsymbol{y} _2 \|^2 \\\\ &= \left\| \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \| ^2} \right\|^2 \\\\ &= \left( \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \| ^2} , \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \| ^2} \right) \\\\ &= \frac{\left( \boldsymbol y , \boldsymbol x \right) }{\| \boldsymbol{x} \| ^2} \left( \boldsymbol x , \frac{\left( \boldsymbol y , \boldsymbol x \right) \boldsymbol x}{\| \boldsymbol{x} \| ^2} \right) \\\\ &= \frac{\left( \boldsymbol y , \boldsymbol x \right) }{\| \boldsymbol{x} \| ^2} \frac{\left( \boldsymbol x , \boldsymbol y \right) }{\| \boldsymbol{x} \| ^2} \left( \boldsymbol x , \boldsymbol x \right) \\\\ &= \frac{\left( \boldsymbol y , \boldsymbol x \right) \left( \boldsymbol x , \boldsymbol y \right)}{\| \boldsymbol{x} \| ^2} \\\\ &= \frac{ \left| \left( \boldsymbol x , \boldsymbol y \right) \right| ^2}{\| \boldsymbol{x} \| ^2} \\\\ \| \boldsymbol{x} \| ^2 \| \boldsymbol{y} \|^2 & \geq \left| \left( \boldsymbol x , \boldsymbol y \right) \right| ^2 \\\\ \| \boldsymbol{x} \| \| \boldsymbol{y} \| & \geq \left| \left( \boldsymbol x , \boldsymbol y \right) \right| \end{align}\] よって、任意の \( n \) 項列ベクトル \( \boldsymbol{x} \) および \( \boldsymbol{y} \) について、シュヴァルツの不等式が成り立ちます。

　三角不等式については、ピタゴラスの定理の証明に用いた立式にシュヴァルツの不等式を適用することで以下のように証明できます。 \[ \begin{align} \| \boldsymbol{x} + \boldsymbol{y} \| ^2 &= \| \boldsymbol{x} \| ^2 + \rm 2 Re \left( \it \boldsymbol x , \boldsymbol y \rm \right) + \| \it \boldsymbol{y} \rm \| ^2 \\\\ & \leq \| \boldsymbol{x} \| ^2 + 2 \left| \left( \boldsymbol x , \boldsymbol y \right) \right| + \| \it \boldsymbol{y} \rm \| ^2 \\\\ & \leq \| \boldsymbol{x} \| ^2 + 2 \| \boldsymbol{x} \| \| \boldsymbol{y} \| + \| \it \boldsymbol{y} \rm \| ^2 \\\\ &= \left( \| \boldsymbol{x} \| + \| \boldsymbol{y} \| \right) ^2 \\\\ \| \boldsymbol{x} + \boldsymbol{y} \| & \leq \| \boldsymbol{x} \| + \| \boldsymbol{y} \| \end{align}\]
　シュヴァルツの不等式に名前が付けられているカール・ヘルマン・アマンドゥス・シュヴァルツは19世紀に活躍したドイツの数学者です。 主に複素解析や微分幾何学の分野に業績を残しました。