目次
・余因子
・余因子展開
・余因子行列
カヤ
今回は余因子について解説する。
余因子
\[ 余因子\]
\( n \) 次正方行列 \( A \) の第 \( i \) 行、第 \( j \) 列を除いてできる \( n-1 \) 次正方行列の行列式を \( A \) の第 \( \left( i, j
\right) \) 小行列式と呼び、
これに \( \left( -1 \right) ^{i+j}\) をかけたものを \( A \) の第 \( \left( i, j \right) \) 余因子と呼ぶ。
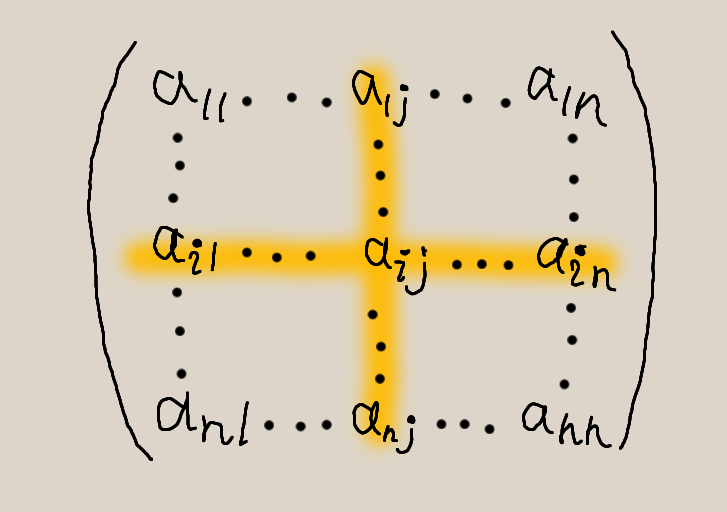
\( n \) 次正方行列が
\[ \begin{align}
A = \left( a_{ij} \right) = \left(
\begin{array}{cccc}
a_{11} & \ldots & a_{1j} & \ldots & a_{1n} \\
\vdots & & \vdots & & \vdots \\
a_{i1} & \ldots & a_{ij} & \ldots & a_{in} \\
\vdots & & \vdots & & \vdots \\
a_{n1} & \ldots & a_{nj} & \ldots & a_{nn}
\end{array}
\right)
\end{align}\]
と表されているとき、この行列の第 \( i \) 行、第 \( j \) 列を除いてできる \( n-1 \) 次正方行列は
\[ \begin{align}
\left(
\begin{array}{cccc}
a_{11} & \ldots & a_{1j-1} & a_{1j+1} & \ldots & a_{1n} \\
\vdots & & \vdots & & \vdots \\
a_{i-11} & \ldots & a_{i-1j-1} & a_{i-1j+1} & \ldots & a_{i-1n} \\
a_{i+11} & \ldots & a_{i+1j-1} & a_{i+1j+1} & \ldots & a_{i+1n} \\
\vdots & & \vdots & & \vdots \\
a_{n1} & \ldots & a_{nj-1} & a_{nj+1} & \ldots & a_{nn}
\end{array}
\right)
\end{align}\]
となり、この行列の行列式を\( A \) の第 \( \left( i, j
\right) \) 小行列式と呼んでいます。
ナユミ
十字型をくり抜くのね。
カヤ
そういう感じだな。続いて、余因子を用いた行列式の展開式について見ていこう。
余因子展開
\[ 余因子展開\]
\( n \) 次行列 \( A = \left( a_{ij} \right) \) の第 \( \left( i,j \right) \) 余因子を \( \tilde{a} _{ij} \)
で表すとき、次の展開式が成り立つ。
\[ \begin{align}
\left| A \right| &= a_{1j} \tilde{a} _{1j} + a _{2j} \tilde{a} _{2j} + \cdots + a _{nj} \tilde{a}
_{nj} \ \ \ \left( j = 1,2, \cdots , n \right) \ \ \ldots \left( 1 \right) \\\\
\left| A \right| &= a_{i1} \tilde{a} _{i1} + a _{i2} \tilde{a} _{i2} + \cdots + a _{in} \tilde{a}
_{in} \ \ \ \left( i = 1,2, \cdots , n \right) \ \ \ldots \left( 2 \right) \\\\
\end{align}\]
\( \left( 1 \right) \) 、\( \left( 2 \right) \) を、それぞれ第 \( j \) 列、第 \( i \) 行に関する行列式の展開と呼ぶ。
行列式についての性質で、列について成り立つ性質は行についても成り立つため、余因子展開については \( \left( 1 \right) \) だけ証明すれば十分です。
\( \left( 1 \right) \) の証明に入る前に、次の補題を証明しておきます。
\[ 補題\]
\[ \begin{align}
\left|
\begin{array}{cccc}
a_{11} & a_{12} & \ldots & a_{1n} \\
0 & a_{22} & \ldots & a_{2n} \\
\vdots & \vdots & & \vdots \\
0 & a_{n2} & \ldots & a_{nn}
\end{array}
\right| = a_{11} \cdot
\left|
\begin{array}{cccc}
a_{22} & \ldots & a_{2n} \\
\vdots & & \vdots \\
a_{n2} & \ldots & a_{nn}
\end{array}
\right|
\end{align}\]
この補題は、行列式の定義
\[ \begin{align}
\sum _{\sigma \in S_n } \rm sgn \ \sigma \cdot \it a_{\rm 1 \it \sigma \rm \left( 1 \right)} \it
a_{\rm 2 \it \sigma \rm \left( 2 \right)} \cdots \it a_{n \sigma \rm \left( \it n \rm \right)}
\end{align}\]
に現れる項 \( a_{\rm 1 \it \sigma \rm \left( 1 \right)} \) について、補題の左辺の行列式の元になる行列を考えると、
\[ \begin{align}
\sigma \left( 1 \right) \neq 1 \ \ ならば \ \ a_{\rm 1 \it \sigma \rm \left( 1 \right)} = 0
\end{align}\]
であることから、行列式の和に現れるのは \( \sigma \left( 1 \right) = 1 \) となる項のみとしてよく、
この場合は \( n-1 \) 文字の置換と考えてよいため、
\[ \begin{align}
\sum _{\sigma \in S_n } \rm sgn \ \sigma \cdot \it a_{\rm 1 \it \sigma \rm \left( 1 \right)} \it
a_{\rm 2 \it \sigma \rm \left( 2 \right)} \cdots \it a_{n \sigma \rm \left( \it n \rm \right)}
= a_{\rm 11} \sum _{\sigma \in S_{n \rm -1} } \rm sgn \ \sigma \cdot \it
a_{\rm 2 \it \sigma \rm \left( 2 \right)} \cdots \it a_{n \sigma \rm \left( \it n \rm \right)}
\end{align}\]
となり補題の式が成り立ちます。
続いて、\( \left( 1 \right) \) の証明に入ります。 なお、以下の証明では、\( A \) の第 \( \left( i, j \right) \) 小行列式を \( \Delta _{ij} \) で表します。
まず、\( j=1 \) の場合を調べます。行列式の列に関する \( n \) 重線型性より、 \[ \begin{align} \left| A \right| = \left| \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| &+ \left| \begin{array}{cccc} 0 & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| + \cdots \\\\ & \cdots + \left| \begin{array}{cccc} 0 & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{array} \right| \end{align}\] この式の右辺の \( i \) 番目の項の行列式について、第 \( i \) 行を互換の繰り返しによって \( 1 \) 行目まで持って行くと、 行列式の交代性により、 \[ \begin{align} \left| A \right| = \left| \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| &- \left| \begin{array}{cccc} a_{21} & a_{22} & \ldots & a_{2n} \\ 0 & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| + \cdots \\\\ & \cdots + \left( -1 \right) ^{n-1} \left| \begin{array}{cccc} a_{n1} & a_{n2} & \ldots & a_{nn} \\ 0 & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n-1,2} & \ldots & a_{n-1,n} \end{array} \right| \end{align}\] ここで、先ほどの補題より、 \[ \begin{align} \left| A \right| = a_{11} \left| \begin{array}{cccc} a_{22} & \ldots & a_{2n} \\ \vdots & & \vdots \\ a_{n2} & \ldots & a_{nn} \end{array} \right| &- a_{21} \left| \begin{array}{cccc} a_{12} & \ldots & a_{1n} \\ \vdots & & \vdots \\ a_{n2} & \ldots & a_{nn} \end{array} \right| + \cdots \\\\ & \cdots + \left( -1 \right) ^{n-1} a_{n1} \left| \begin{array}{cccc} a_{12} & \ldots & a_{1n} \\ \vdots & & \vdots \\ a_{n-1,2} & \ldots & a_{n-1,n} \end{array} \right| \end{align}\] よって、 \[ \begin{align} \left| A \right| &= a_{11} \Delta _{11} - a_{21} \Delta _{21} + \cdots + \left( -1 \right) ^{n-1} a_{n1} \Delta _{n1} \\\\ &= a_{11} \tilde{a} _{11} + a_{21} \tilde{a} _{21} + \cdots + a_{n1} \tilde{a} _{n1} \end{align}\] となり、\( j=1 \) の場合について \( \left( 1 \right) \) が証明されました。
一般の \( j \) に対しては、行列式の第 \( j \) 列を互換の繰り返しにより 1 列目まで持ってくると、 行列式は \( \left( -1 \right) ^{j-1} = \left( -1 \right) ^{j+1}\) 倍されるため、\( j=1 \) のときの結果より、 \[ \begin{align} \left( -1 \right) ^{j+1} \left| A \right| &= a_{1j} \Delta _{1j} - a_{2j} \Delta _{2j} + \cdots + \left( -1 \right) ^{n-1} a_{nj} \Delta _{nj} \\\\ &= \left( -1 \right) ^{-j-1} \cdot \left( -1 \right) ^{j+1} \left\{ a_{1j} \Delta _{1j} - a_{2j} \Delta _{2j} + \cdots + \left( -1 \right) ^{n-1} a_{nj} \Delta _{nj} \right\} \\\\ &= \left( -1 \right) ^{-j-1} \left( a_{1j} \tilde{a} _{1j} + a_{2j} \tilde{a} _{2j} + \cdots + a_{nj} \tilde{a} _{nj} \right) \\\\ \left| A \right| &= \left( -1 \right) ^{-2 \left( j + 1\right) } \left( a_{1j} \tilde{a} _{1j} + a_{2j} \tilde{a} _{2j} + \cdots + a_{nj} \tilde{a} _{nj} \right) \\\\ &= a_{1j} \tilde{a} _{1j} + a_{2j} \tilde{a} _{2j} + \cdots + a_{nj} \tilde{a} _{nj} \end{align}\] となり、一般の \( j \) についても \( \left( 1 \right) \) が証明されたことになります。
次に、余因子展開を少し拡張した定理を見ておきます。
続いて、\( \left( 1 \right) \) の証明に入ります。 なお、以下の証明では、\( A \) の第 \( \left( i, j \right) \) 小行列式を \( \Delta _{ij} \) で表します。
まず、\( j=1 \) の場合を調べます。行列式の列に関する \( n \) 重線型性より、 \[ \begin{align} \left| A \right| = \left| \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| &+ \left| \begin{array}{cccc} 0 & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| + \cdots \\\\ & \cdots + \left| \begin{array}{cccc} 0 & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{array} \right| \end{align}\] この式の右辺の \( i \) 番目の項の行列式について、第 \( i \) 行を互換の繰り返しによって \( 1 \) 行目まで持って行くと、 行列式の交代性により、 \[ \begin{align} \left| A \right| = \left| \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ 0 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| &- \left| \begin{array}{cccc} a_{21} & a_{22} & \ldots & a_{2n} \\ 0 & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n2} & \ldots & a_{nn} \end{array} \right| + \cdots \\\\ & \cdots + \left( -1 \right) ^{n-1} \left| \begin{array}{cccc} a_{n1} & a_{n2} & \ldots & a_{nn} \\ 0 & a_{12} & \ldots & a_{1n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{n-1,2} & \ldots & a_{n-1,n} \end{array} \right| \end{align}\] ここで、先ほどの補題より、 \[ \begin{align} \left| A \right| = a_{11} \left| \begin{array}{cccc} a_{22} & \ldots & a_{2n} \\ \vdots & & \vdots \\ a_{n2} & \ldots & a_{nn} \end{array} \right| &- a_{21} \left| \begin{array}{cccc} a_{12} & \ldots & a_{1n} \\ \vdots & & \vdots \\ a_{n2} & \ldots & a_{nn} \end{array} \right| + \cdots \\\\ & \cdots + \left( -1 \right) ^{n-1} a_{n1} \left| \begin{array}{cccc} a_{12} & \ldots & a_{1n} \\ \vdots & & \vdots \\ a_{n-1,2} & \ldots & a_{n-1,n} \end{array} \right| \end{align}\] よって、 \[ \begin{align} \left| A \right| &= a_{11} \Delta _{11} - a_{21} \Delta _{21} + \cdots + \left( -1 \right) ^{n-1} a_{n1} \Delta _{n1} \\\\ &= a_{11} \tilde{a} _{11} + a_{21} \tilde{a} _{21} + \cdots + a_{n1} \tilde{a} _{n1} \end{align}\] となり、\( j=1 \) の場合について \( \left( 1 \right) \) が証明されました。
一般の \( j \) に対しては、行列式の第 \( j \) 列を互換の繰り返しにより 1 列目まで持ってくると、 行列式は \( \left( -1 \right) ^{j-1} = \left( -1 \right) ^{j+1}\) 倍されるため、\( j=1 \) のときの結果より、 \[ \begin{align} \left( -1 \right) ^{j+1} \left| A \right| &= a_{1j} \Delta _{1j} - a_{2j} \Delta _{2j} + \cdots + \left( -1 \right) ^{n-1} a_{nj} \Delta _{nj} \\\\ &= \left( -1 \right) ^{-j-1} \cdot \left( -1 \right) ^{j+1} \left\{ a_{1j} \Delta _{1j} - a_{2j} \Delta _{2j} + \cdots + \left( -1 \right) ^{n-1} a_{nj} \Delta _{nj} \right\} \\\\ &= \left( -1 \right) ^{-j-1} \left( a_{1j} \tilde{a} _{1j} + a_{2j} \tilde{a} _{2j} + \cdots + a_{nj} \tilde{a} _{nj} \right) \\\\ \left| A \right| &= \left( -1 \right) ^{-2 \left( j + 1\right) } \left( a_{1j} \tilde{a} _{1j} + a_{2j} \tilde{a} _{2j} + \cdots + a_{nj} \tilde{a} _{nj} \right) \\\\ &= a_{1j} \tilde{a} _{1j} + a_{2j} \tilde{a} _{2j} + \cdots + a_{nj} \tilde{a} _{nj} \end{align}\] となり、一般の \( j \) についても \( \left( 1 \right) \) が証明されたことになります。
次に、余因子展開を少し拡張した定理を見ておきます。
\[ 余因子展開の拡張\]
\[ \begin{align}
\delta _{jl} \left| A \right| &= a_{1j} \tilde{a} _{1l} + a _{2j} \tilde{a} _{2l} + \cdots + a _{nj}
\tilde{a}
_{nl} \ \ \ \left( j,l = 1,2, \cdots , n \right) \ \ \ldots \left( 3 \right) \\\\
\delta _{ik} \left| A \right| &= a_{i1} \tilde{a} _{k1} + a _{i2} \tilde{a} _{k2} + \cdots + a _{in}
\tilde{a}
_{kn} \ \ \ \left( i,k = 1,2, \cdots , n \right) \ \ \ldots \left( 4 \right) \\\\
\end{align}\]
ただし、
\[ \begin{align}
\delta _{IJ} =
\begin{cases}
1 \ \ \left( I = J \right) \\
0 \ \ \left( I \neq J \right)
\end{cases}
\end{align}\]
である。
\( \left( 3 \right) \) のみ証明します。
\( j=l \) の場合、先ほどの定理の \( \left( 1 \right) \) となります。
\( j \neq l \) の場合、\( \left( 3 \right) \) の右辺は、\( A \) の第 \( l \) 列を第 \( j \) 列で置き換えた行列の第 \( l \)
列に関する展開式になります。
この行列は、第 \( l \) 列と第 \( j \) 列が等しいため、行列式の値は \( 0 \) となります。以上より、\( \left( 3 \right) \) が成り立ちます。
カヤ
あとは、逆行列との関係が深い余因子行列というものを見ておこう。
余因子行列
\[ 余因子行列\]
\( \tilde{a} _{ji} \) を \( \left( i,j \right) \) 成分とする \( n \) 次行列を \( A \) の余因子行列と呼び、\(
\tilde{A} \) で表す。すなわち、
\[ \begin{align}
\tilde{A} = \left(
\begin{array}{cccc}
\tilde{a}_{11} & \tilde{a}_{21} & \ldots & \tilde{a}_{n1} \\
\tilde{a}_{12} & \tilde{a}_{22} & \ldots & \tilde{a}_{n2} \\
\vdots & \vdots & & \vdots \\
\tilde{a}_{1n} & \tilde{a}_{2n} & \ldots & \tilde{a}_{nn}
\end{array}
\right)
\end{align}\]
である。余因子行列について、次が成り立つ。
\[ \begin{align}
\tilde{A} A = A \tilde{A} = \left| A \right| \cdot E_n \ \ldots \left( 5 \right)
\end{align}\]
\( \left( 3 \right) \) 式と \( \left( 4 \right) \) 式の左辺は、それぞれ行列 \( \tilde{A}A \) の \( \left( l,j\right) \) 成分
および行列 \( A \tilde{A} \) の \( \left( i,k \right) \) 成分を表しています。
一方、\( \left( 3 \right) \) 式と \( \left( 4 \right) \) 式の右辺は行列 \( \left| A \right| \cdot E_n \) の \( \left( l,j
\right) \) 成分および \( \left( i,k \right) \) 成分であるため、\( \left( 5 \right) \) 式が成り立ちます。
\( \left( 5 \right) \) 式より、逆行列の表式を与える次の定理が成り立ちます。
\( \left( 5 \right) \) 式より、逆行列の表式を与える次の定理が成り立ちます。
\( n \) 次行列 \( A \) が正則であるためには、\( \left| A \right| \neq 0 \) が必要十分条件である。
このとき、逆行列は
\[ \begin{align}
A^{-1} = \frac{1}{\left| A \right|} \tilde{A}
\end{align}\]
で与えられる。
カヤ
次回は上の定理を使って連立一次方程式について考察していこう。
参考：
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行
前の記事
第34話
行列式
行列式
次の記事
第36話
クラメルの公式
クラメルの公式