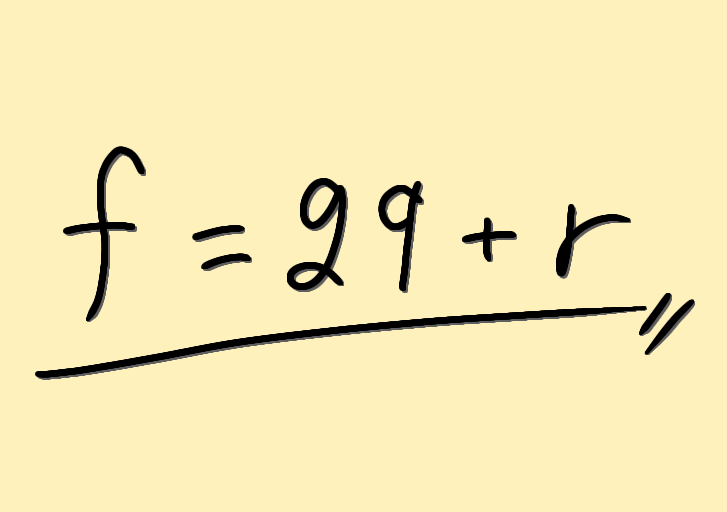
目次
・\( x \)-行列
・単因子
・\( n \) 次 \( x \)-行列の商と余り
・特性 \( x \)-行列
\( x \)-行列
以下では、一変数 \( x \) の \( \mathbb C \) -係数多項式を成分とする行列を \( x \)-行列と呼び、\( A(x) \) などと表します。
\( \mathbb C \) の元、すなわち複素数は 0 次多項式であるため、通常の行列は \( x \)-行列とみなせます。
2 つの \( x \)-行列の和、積は通常の行列同様に定義されて、それらは \( x \)-行列となり、同様の演算法則が成り立ちます。 \( n \) 次 \( x \)-行列については、行列式も同様に定義され、\( x \) の多項式になります。
\( n \) 次 \( x \)-行列 \( A(x) \) について、 \[ \begin{align} X(x) A(x) = A(x) X(x) = E \end{align}\] を満たす \( n \) 次 \( x \)-行列 \( X(x) \) が存在するとき、\( A(x) \) を可逆行列と呼びます。 \( A(x) \) が可逆行列なら、上の式を満たす \( X(x) \) はただ一つしかなく、これを \( A(x) \) の逆行列と呼び、\( A(x) ^{-1} \) で表します。
可逆行列について、次の定理が成り立ちます。
\( \mathbb C \) の元、すなわち複素数は 0 次多項式であるため、通常の行列は \( x \)-行列とみなせます。
2 つの \( x \)-行列の和、積は通常の行列同様に定義されて、それらは \( x \)-行列となり、同様の演算法則が成り立ちます。 \( n \) 次 \( x \)-行列については、行列式も同様に定義され、\( x \) の多項式になります。
\( n \) 次 \( x \)-行列 \( A(x) \) について、 \[ \begin{align} X(x) A(x) = A(x) X(x) = E \end{align}\] を満たす \( n \) 次 \( x \)-行列 \( X(x) \) が存在するとき、\( A(x) \) を可逆行列と呼びます。 \( A(x) \) が可逆行列なら、上の式を満たす \( X(x) \) はただ一つしかなく、これを \( A(x) \) の逆行列と呼び、\( A(x) ^{-1} \) で表します。
可逆行列について、次の定理が成り立ちます。
\[ \begin{align}
可逆行列の同値条件
\end{align}\]
\( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であることは、行列式 \( | A(x) | \) が \( \mathbb C \) の 0
でない元であることの必要十分条件である。
\( A(x) \) が可逆行列であれば、逆行列 \( A(x)^{-1} \) が存在します。よって、
\[ \begin{align}
\left| A(x) \right| \left| A(x) ^{-1} \right| = \left| A(x) A(x) ^{-1} \right| = |E| = 1
\end{align}\]
が成り立ちます。ここで、\( \left| A(x) \right| \) も \( \left| A(x) ^{-1} \right| \) も \( x \) の多項式であるため、これらを掛けあわせたものが 0
でない \( \mathbb C \) の元であるなら、次が成り立ちます。
\[ \begin{align}
| A(x) | \in \mathbb C \ \text{かつ} \ | A(x) | \neq 0
\end{align}\]
今、\( \left| A(x) \right| \left| A(x) ^{-1} \right| = 1 \) であるため、この条件は成り立ちます。
逆に、\( |A(x)| \) が \( \mathbb C \) の 0 でない元であれば、\( A(x) \) の余因子行列を\( \tilde{A} (x) \) とすれば、 \[ \begin{align} \tilde{A} (x) A(x) = A(x) \tilde{A} (x) = | A(x) | \cdot E \end{align}\] が成り立つため、\( A(x) \) は \( \tilde{A} (x) / |A(x)| \) を逆行列とする可逆行列になります。
なお、ここで正則行列ではなく可逆行列という言葉を用いているのは、\( n \) 次 \( x \)-行列においては、通常の行列のように逆行列の存在を他の様々な定理の同値条件と扱えないことによります。 例えば、次の 2 次 \( x \)-行列 \[ \begin{align} A(x) = \left( \begin{array}{cc} 1 & 0 \\ 0 & x \end{array} \right) \end{align}\] を考えます。この行列の線形独立な列ベクトルの最大数は 2 であり、これは通常の行列であれば逆行列の存在を示す条件です。 ところが、 \[ \begin{align} \left( \begin{array}{cc} 1 & 0 \\ 0 & x \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & \frac{1}{x} \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \end{align}\] であるため、\( A(x) \) の逆行列となり得る行列は 2 次 \( x \)-行列ではなく(\( 1/x \) は多項式ではない)、逆行列は存在しないことになります。
逆に、\( |A(x)| \) が \( \mathbb C \) の 0 でない元であれば、\( A(x) \) の余因子行列を\( \tilde{A} (x) \) とすれば、 \[ \begin{align} \tilde{A} (x) A(x) = A(x) \tilde{A} (x) = | A(x) | \cdot E \end{align}\] が成り立つため、\( A(x) \) は \( \tilde{A} (x) / |A(x)| \) を逆行列とする可逆行列になります。
なお、ここで正則行列ではなく可逆行列という言葉を用いているのは、\( n \) 次 \( x \)-行列においては、通常の行列のように逆行列の存在を他の様々な定理の同値条件と扱えないことによります。 例えば、次の 2 次 \( x \)-行列 \[ \begin{align} A(x) = \left( \begin{array}{cc} 1 & 0 \\ 0 & x \end{array} \right) \end{align}\] を考えます。この行列の線形独立な列ベクトルの最大数は 2 であり、これは通常の行列であれば逆行列の存在を示す条件です。 ところが、 \[ \begin{align} \left( \begin{array}{cc} 1 & 0 \\ 0 & x \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & \frac{1}{x} \end{array} \right) = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) \end{align}\] であるため、\( A(x) \) の逆行列となり得る行列は 2 次 \( x \)-行列ではなく(\( 1/x \) は多項式ではない)、逆行列は存在しないことになります。
単因子
3 種類の基本行列 \( P_n \left( i , j \right) \) 、\( Q_n \left( i ; \ c \right) \) 、\( R_n \left( i,j ; \ c
\right) \) の内、\( R_n \left( i,j ; \ c \right) \) の数 \( c \) の代わりに \( x \) の多項式 \( c(x) \) を入れたものを \( R_n
\left( i,j ; \ c(x) \right) \) で表し、これも基本行列と呼ぶことにします。
\( R_n \left( i,j ; \ c(x) \right) \) の逆行列は \( R_n \left( i,j ; \ -c(x) \right) \) です。
2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が、何回かの基本変形によって移り合うとき、\( A(x) \) と \( B(x) \) は対等であると言います。
以上の条件のもとで、次の定理が成り立ちます。
2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が、何回かの基本変形によって移り合うとき、\( A(x) \) と \( B(x) \) は対等であると言います。
以上の条件のもとで、次の定理が成り立ちます。
\[ \begin{align}
スミス標準形
\end{align}\]
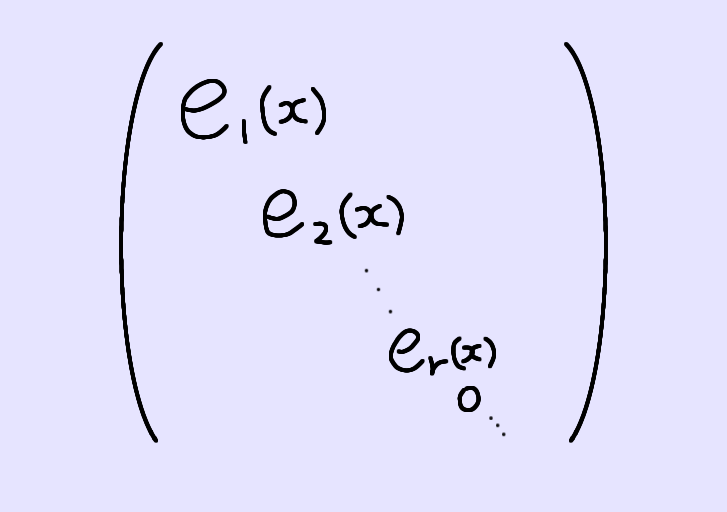
任意の \( n \) 次 \( x \)-行列 \( A(x) \) は次のスミス標準形と呼ばれる対角行列と対等である。
\[ \begin{align}
\left(
\begin{array}{ccccc}
e_1 (x) & & & & & & \\
& e_2 (x) & & & & & \\
& & \ddots & & & & \\
& & & e_r (x) & & & \\
& & & & 0 & & \\
& & & & & \ddots & \\
& & & & & & 0
\end{array}
\right)
\end{align}\]
ここで、\( e_1 (x), e_2 (x) , \cdots , e_r (x) \) は次の条件を満たす:
[1] \( e_i (x) \ \left( i = 1,2, \cdots, r \right) \) は最高次係数が 1 の多項式である。
[2] \( e_i (x) \) は \( e_{i-1} (x) \) で割り切れる \( \left( i = 2,3, \cdots , r \right) \)
また、スミス標準形は \( A(x) \) により一意的に定まる。
[1] \( e_i (x) \ \left( i = 1,2, \cdots, r \right) \) は最高次係数が 1 の多項式である。
[2] \( e_i (x) \) は \( e_{i-1} (x) \) で割り切れる \( \left( i = 2,3, \cdots , r \right) \)
また、スミス標準形は \( A(x) \) により一意的に定まる。
\( A(x) \) によって決まる数 \( r \) を \( A(x) \) の階数と呼び、\( r \) 個の多項式
\[ e_1 (x), e_2 (x) , \cdots , e_r (x) \]
を \( A(x) \) の単因子と呼びます。
これらは、成分が複素数である通常の行列に対して定義された階数の拡張になっています。
実際、\( e_i (x) \ \left( i = 1,2, \cdots, r \right) \) がすべて 0 次の多項式であるなら、[1] の条件より単因子はすべて 1 に等しく、スミス標準形は
\[ \begin{align}
F_{n, \ n} \left( r \right) &=
\left(
\begin{array}{cc}
E_{r} & O_{r, \ n-r} \\
O_{n-r, \ r} & O_{n-r, \ n-r}
\end{array}
\right)
\end{align}\]
となります。
ここから、上の定理を証明していきます。 まず、任意の \( n \) 次 \( x \)-行列 \( A(x) \) はスミス標準形と対等であることを数学的帰納法により示します。
1) \( n=1 \) のとき
\( A(x) \) の \( \left( 1,1 \right) \) 成分の最高次係数で \( A(x) \) を割れば、これはスミス標準形です。
2) \( n=k \gt 1\) とし、任意の \( k - 1 \) 次 \( x \)-行列はスミス標準形と対等であると仮定
\( A(x) = O \) なら、これはスミス標準形であるため、\( A(x) \neq O \) とします。 \( A(x) \neq O \) であるため、\( A(x) \) と対等な行列で、\( \left( 1,1 \right) \) 成分が 0 でないものが少なくとも一つ存在します。 このような行列全体の中で、\( \left( 1,1 \right) \) 成分の次数が最低であるようなものの一つを取ります。 この行列の第 1 行を \( \left( 1,1 \right) \) 成分の最高次係数で割ると、\( A(x) \) と対等な行列 \[ \begin{align} B \left( x \right) &= \left( \begin{array}{cccc} e_1 (x) & b_{12} (x) & \cdots & b_{1k} (x) \\ b_{21} (x) & b_{22} (x) & \cdots & b_{2k} (x) \\ \vdots & \vdots & & \vdots \\ b_{k1} (x) & b_{k2} (x) & \cdots & b_{kk} (x) \end{array} \right) \end{align}\] が得られます。ここで、\( e_1 (x) \) の最高次係数は 1 となっていることに注意します。
次に、\( B(x) \) の第 1 行および第 1 列の成分はすべて \( e_1 (x) \) で割り切れることを示します。 もし、\( b_{1j} (x) \ \left( j \neq 1 \right) \) が \( e_1 (x) \) で割り切れないなら、 \[ \begin{align} b_{1j} (x) = e_1 (x) q(x) + r(x) \end{align}\] が成り立つような多項式 \( q(x) \) と、\( e_1 (x) \) より次数の低い多項式 \( r(x) \) が存在します。 このとき、\( B(x) \) の第 \( j \) 列から第 1 列の \( q(x) \) 倍を引き、その後第 1 列と第 \( j \) 列を交換すると、\( \left( 1,1 \right) \) 成分が \( r(x) \) であり、\( A(x) \) と対等な行列が得られます。 しかし、\( \left( 1,1 \right) \) 成分 \( r(x) \) の次数が \( e_1 (x) \) より低いことは、\( B(x) \) の作り方に反しています。 よって、\( b_{1j} (x) \ \left( j \neq 1 \right) \) は \( e_1 (x) \) で割り切れます。
\( b_{i1} (x) \ \left( i \neq 1 \right) \) が \( e_1 (x) \) で割り切れることも同様に示せます。
よって、\( b_{1j} (x) = e_1 (x) q_j (x) \) 、\( b_{i1} (x) = e_1 (x) q_i (x) \) と置くことができ、\( B(x) \) の第 \( j \) 列から第 1 列の \( q_j (x) \) 倍を引き、第 \( i \) 行から第 1 行の \( q_i (x) \) 倍を引くと、 \[ \begin{align} C \left( x \right) &= \left( \begin{array}{cccc} e_1 (x) & 0 & \cdots & 0 \\ 0 & c_{22} (x) & \cdots & c_{2k} (x) \\ \vdots & \vdots & & \vdots \\ 0 & c_{k2} (x) & \cdots & c_{kk} (x) \end{array} \right) \end{align}\] が得られます。ここで、\( k-1 \) 次行列 \[ \begin{align} \left( \begin{array}{ccc} c_{22} (x) & \cdots & c_{2k} (x) \\ \vdots & & \vdots \\ c_{k2} (x) & \cdots & c_{kk} (x) \end{array} \right) \end{align}\] は、数学的帰納法の仮定により、何回かの基本変形により、スミス標準形 \[ \begin{align} \left( \begin{array}{cccccc} e_{2} (x) & & & & & \\ & \ddots & & & & \\ & & e_{r} (x) & & & \\ & & & 0 & & \\ & & & & \ddots & \\ & & & & & 0 \end{array} \right) \end{align}\] に移ります。これと同じ基本変形を \( C(x) \) に施すと、\( A(x) \) と対等な行列 \[ \begin{align} D \left( x \right) &= \left( \begin{array}{ccccccc} e_{1} (x) & & & & & & \\ & e_{2} (x) & & & & & \\ & & \ddots & & & & \\ & & & e_{r} (x) & & & \\ & & & & 0 & & \\ & & & & & \ddots & \\ & & & & & & 0 \end{array} \right) \end{align}\] が得られます。
続いて、\( e_2 (x) \) が \( e_1 (x) \) により割り切れることを示します。 もし、\( e_2 (x) \) が \( e_1 (x) \) により割り切れないとすると、 \[ \begin{align} e_{2} (x) = e_1 (x) q(x) + r(x) \end{align}\] が成り立つような多項式 \( q(x) \) と、\( e_1 (x) \) より次数の低い多項式 \( r(x) \) が存在します。 このとき、\( D (x) \) の第 2 列に第 1 列の \( q(x) \) 倍を加え、その後第 2 行から第 1 行を引くと、\( \left( 2, 2 \right) \) 成分は \( r(x) \) になります。 この \( r(x) \) は基本変形によって \( \left( 1, 1 \right) \) 成分に移すことができますが、これは \( B(x) \) の作り方に反しています。
よって、\( e_2 (x) \) は \( e_1 (x) \) により割り切れ、\( D(x) \) はスミス標準形になります。
1)、2)より、任意の \( n \) 次 \( x \)-行列 \( A(x) \) はスミス標準形と対等であることが示せました。
ここから、上の定理を証明していきます。 まず、任意の \( n \) 次 \( x \)-行列 \( A(x) \) はスミス標準形と対等であることを数学的帰納法により示します。
1) \( n=1 \) のとき
\( A(x) \) の \( \left( 1,1 \right) \) 成分の最高次係数で \( A(x) \) を割れば、これはスミス標準形です。
2) \( n=k \gt 1\) とし、任意の \( k - 1 \) 次 \( x \)-行列はスミス標準形と対等であると仮定
\( A(x) = O \) なら、これはスミス標準形であるため、\( A(x) \neq O \) とします。 \( A(x) \neq O \) であるため、\( A(x) \) と対等な行列で、\( \left( 1,1 \right) \) 成分が 0 でないものが少なくとも一つ存在します。 このような行列全体の中で、\( \left( 1,1 \right) \) 成分の次数が最低であるようなものの一つを取ります。 この行列の第 1 行を \( \left( 1,1 \right) \) 成分の最高次係数で割ると、\( A(x) \) と対等な行列 \[ \begin{align} B \left( x \right) &= \left( \begin{array}{cccc} e_1 (x) & b_{12} (x) & \cdots & b_{1k} (x) \\ b_{21} (x) & b_{22} (x) & \cdots & b_{2k} (x) \\ \vdots & \vdots & & \vdots \\ b_{k1} (x) & b_{k2} (x) & \cdots & b_{kk} (x) \end{array} \right) \end{align}\] が得られます。ここで、\( e_1 (x) \) の最高次係数は 1 となっていることに注意します。
次に、\( B(x) \) の第 1 行および第 1 列の成分はすべて \( e_1 (x) \) で割り切れることを示します。 もし、\( b_{1j} (x) \ \left( j \neq 1 \right) \) が \( e_1 (x) \) で割り切れないなら、 \[ \begin{align} b_{1j} (x) = e_1 (x) q(x) + r(x) \end{align}\] が成り立つような多項式 \( q(x) \) と、\( e_1 (x) \) より次数の低い多項式 \( r(x) \) が存在します。 このとき、\( B(x) \) の第 \( j \) 列から第 1 列の \( q(x) \) 倍を引き、その後第 1 列と第 \( j \) 列を交換すると、\( \left( 1,1 \right) \) 成分が \( r(x) \) であり、\( A(x) \) と対等な行列が得られます。 しかし、\( \left( 1,1 \right) \) 成分 \( r(x) \) の次数が \( e_1 (x) \) より低いことは、\( B(x) \) の作り方に反しています。 よって、\( b_{1j} (x) \ \left( j \neq 1 \right) \) は \( e_1 (x) \) で割り切れます。
\( b_{i1} (x) \ \left( i \neq 1 \right) \) が \( e_1 (x) \) で割り切れることも同様に示せます。
よって、\( b_{1j} (x) = e_1 (x) q_j (x) \) 、\( b_{i1} (x) = e_1 (x) q_i (x) \) と置くことができ、\( B(x) \) の第 \( j \) 列から第 1 列の \( q_j (x) \) 倍を引き、第 \( i \) 行から第 1 行の \( q_i (x) \) 倍を引くと、 \[ \begin{align} C \left( x \right) &= \left( \begin{array}{cccc} e_1 (x) & 0 & \cdots & 0 \\ 0 & c_{22} (x) & \cdots & c_{2k} (x) \\ \vdots & \vdots & & \vdots \\ 0 & c_{k2} (x) & \cdots & c_{kk} (x) \end{array} \right) \end{align}\] が得られます。ここで、\( k-1 \) 次行列 \[ \begin{align} \left( \begin{array}{ccc} c_{22} (x) & \cdots & c_{2k} (x) \\ \vdots & & \vdots \\ c_{k2} (x) & \cdots & c_{kk} (x) \end{array} \right) \end{align}\] は、数学的帰納法の仮定により、何回かの基本変形により、スミス標準形 \[ \begin{align} \left( \begin{array}{cccccc} e_{2} (x) & & & & & \\ & \ddots & & & & \\ & & e_{r} (x) & & & \\ & & & 0 & & \\ & & & & \ddots & \\ & & & & & 0 \end{array} \right) \end{align}\] に移ります。これと同じ基本変形を \( C(x) \) に施すと、\( A(x) \) と対等な行列 \[ \begin{align} D \left( x \right) &= \left( \begin{array}{ccccccc} e_{1} (x) & & & & & & \\ & e_{2} (x) & & & & & \\ & & \ddots & & & & \\ & & & e_{r} (x) & & & \\ & & & & 0 & & \\ & & & & & \ddots & \\ & & & & & & 0 \end{array} \right) \end{align}\] が得られます。
続いて、\( e_2 (x) \) が \( e_1 (x) \) により割り切れることを示します。 もし、\( e_2 (x) \) が \( e_1 (x) \) により割り切れないとすると、 \[ \begin{align} e_{2} (x) = e_1 (x) q(x) + r(x) \end{align}\] が成り立つような多項式 \( q(x) \) と、\( e_1 (x) \) より次数の低い多項式 \( r(x) \) が存在します。 このとき、\( D (x) \) の第 2 列に第 1 列の \( q(x) \) 倍を加え、その後第 2 行から第 1 行を引くと、\( \left( 2, 2 \right) \) 成分は \( r(x) \) になります。 この \( r(x) \) は基本変形によって \( \left( 1, 1 \right) \) 成分に移すことができますが、これは \( B(x) \) の作り方に反しています。
よって、\( e_2 (x) \) は \( e_1 (x) \) により割り切れ、\( D(x) \) はスミス標準形になります。
1)、2)より、任意の \( n \) 次 \( x \)-行列 \( A(x) \) はスミス標準形と対等であることが示せました。
次に、スミス標準形が \( A(x) \) により一意的に定まることを示します。準備として、いくつかの用語を定義します。
\[ \begin{align}
k \ \text{次小行列式}
\end{align}\]
\( \left( m, n \right) \) 型 \( x \)-行列 \( A(x) \) から勝手に \( k \) 個 \( \left( k \leq m \ \text{かつ}\ k
\leq n
\right) \) の行と列
\[ \begin{align}
i_1, i_2, \cdots , i_k \ \left( 1 \leq i_1 \lt i_2 \lt \cdots \lt i_k \leq m \right) \\\\
j_1, j_2, \cdots , j_k \ \left( 1 \leq j_1 \lt j_2 \lt \cdots \lt j_k \leq n \right)
\end{align}\]
を選び作った \( k \) 次 \( x \)-行列の行列式
\[ \begin{align}
\left|
\begin{array}{cccc}
a_{i_1 j_1} & a_{i_1 j_2} & \ldots & a_{i_1 j_k} \\
a_{i_2 j_1} & a_{i_2 j_2} & \ldots & a_{i_2 j_k} \\
\vdots & \vdots & & \vdots \\
a_{i_k j_1} & a_{i_k j_2} & \ldots & a_{i_k j_k}
\end{array}
\right|
\end{align}\]
を、\( A(x) \) の \( k \) 次小行列式と呼ぶ。
続いて、\( k \) 次小行列式を用いて、行列式因子を定義します。
\[ \begin{align}
k \ \text{次行列式因子}
\end{align}\]
\( n \) 次 \( x \)-行列 \( A(x) \) のすべての \( k \) 次小行列式の最大公約数(ただし、最高次係数は 1 とする)を、\( A(x) \) の \( k \)
次行列式因子と呼び、\( d_k (x) \) で表す。
もし、\( k \) 次小行列式がすべて 0 のときは、\( d_k (x) = 0 \) とする。
それでは、一意性を示すために必要な次の定理を証明します。
\[ \begin{align}
行列式因子の不変性
\end{align}\]
互いに対等な \( n \) 次 \( x \)-行列の \( n \) 個の行列式因子は一致する。
互いに対等な \( x \)-行列は何回かの基本変形により移り合うため、\( n \) 次 \( x \)-行列 \( A(x) \)
に基本変形を施したときに、行列式因子が変わらないことを示せば、上の定理を証明したことになります。
3 種類の基本変形の内、行または列の交換を施した場合、交換された行または列を含む小行列式の値は \( -1 \) 倍されます(互換の符号が \( -1 \) であることを思い出してください)。 しかし、これによって \( k \) 次小行列式の最大公約数が変わることはありません。
また、ある行または列に 0 でない複素数 \( c \) をかけた場合、かけられた行または列を含む小行列式の値は \( c \) 倍されますが、これによって \( k \) 次小行列式の最大公約数が変わることもありません。
よって、行または列の交換および、ある行または列に 0 でない複素数 \( c \) をかけるという 2 種類の基本変形については行列式因子を変えないことが示せました。
そこで、残る 1 種類の基本変形、すなわち、 \( A(x) \) の第 \( i \) 行(あるいは列)に第 \( j \) 行(あるいは列) \( \left( i \neq j \right) \) の \( c(x) \) 倍を加える操作について考えます。 この操作で得られる行列を \( A ^{\blacktriangledown} (x) \) とし、\( A ^{\blacktriangledown} (x) \) の \( k \) 次行列式因子を \( d_k ^ {\blacktriangledown} (x)\) とします。 行列式の性質で行に関して成り立つものは列についても成り立つので、以下では行についての操作を考えます。
\( A(x) \) の \( k \) 次小行列式のうち、第 \( i \) 行を含まないものはこの操作では変わりません。 また、第 \( i \) 行と第 \( j \) 行をどちらも含むものもこの操作では変わりません。
そこで、\( A(x) \) の \( k \) 次小行列式 \( \Delta (x) \) が第 \( i \) 行を含み、第 \( j \) 行を含まないとします。 \( \Delta (x) \) と対応する行列 \( A ^{\blacktriangledown} (x) \) における小行列式を \( \Delta ^{\blacktriangledown} (x) \) とします。 また、\( \Delta (x) \) に含まれる \( A(x) \) の第 \( i \) 行を第 \( j \) 行で置き換えたものを \( \Delta _1 (x) \) とします。 すると、次式が成り立ちます。 \[ \begin{align} \Delta ^{\blacktriangledown} (x) = \Delta (x) + c(x) \Delta _1 (x) \end{align}\] \( \Delta (x) \) と \( \Delta _1 (x) \) はいずれも \( A(x) \) の小行列式であるため、これらは \( d_k (x) \) で割り切れます。 従って、\( \Delta ^{\blacktriangledown} (x) \) も \( d_k (x) \) で割り切れます。
以上より、\( A ^{\blacktriangledown} (x) \) のすべての \( k \) 次小行列式は \( d_k (x) \) で割り切れるため、その最大公約数 \( d_k ^ {\blacktriangledown} (x) \) は \( d_k (x) \) で割り切れます。 つまり、 \[ \begin{align} d_k ^ {\blacktriangledown} (x) = d_k (x) q_1 (x) \end{align}\] を満たす \( \mathbb C \)-係数多項式 \( q_1 (x) \) が存在します。
また、基本行列はいずれも正則行列であるため、逆行列が存在します。よって、以上の考察は \( A ^{\blacktriangledown} (x) \) を \( A (x) \) へ移すときにも成り立ちます。 そのため、\( d_k (x) \) は \( d_k ^ {\blacktriangledown} (x) \) で割り切れます。 ゆえに、 \[ \begin{align} d_k (x) = d_k ^ {\blacktriangledown} (x) q_2 (x) \end{align}\] を満たす \( \mathbb C \)-係数多項式 \( q_2 (x) \) が存在します。従って、 \[ \begin{align} d_k (x) &= d_k ^ {\blacktriangledown} (x) q_2 (x) \\\\ &= d_k (x) q_1 (x) q_2 (x) \\\\ q_1 (x) q_2 (x) &= 1 \end{align}\] が成り立ちます。よって、\( q_1 (x) \) と \( q_2 (x) \) はいずれも 0 次多項式、つまり複素数となりますが、\( d_k (x) \) と \( d_k ^ {\blacktriangledown} (x) \) の最高次係数はいずれも 1 であるため、\( q_1 (x) = q_2 (x) = 1 \) が成り立ちます。 よって、\( d_k (x) = d_k ^ {\blacktriangledown} (x) \) が成り立ち、\( n \) 次 \( x \)-行列 \( A(x) \) に基本変形を施したときに、行列式因子が変わらないことが示せました。
それでは、スミス標準形の一意性を証明します。 \( n \) 次 \( x \)-行列 \( A(x) \) およびそのスミス標準形 \( D(x) \) の行列式因子を \( d_1 (x), d_2 (x) , \cdots , d_n (x) \) とします。
まず、\( k \leq r \) のときを考えます。 対角行列の行列式は、その対角成分の積に等しいことを思い出すと、\( D(x) \) の \( k \) 次小行列式は 0 であるか、\( A(x) \) の単因子 \( e_1 (x), e_2 (x) , \cdots , e_r (x) \) から重複なしで任意に選んだ \( k \) 個の積になります。 0 は任意の多項式で割り切れることと、\( e_i (x) \) は \( e_{i-1} (x) \) で割り切れる \( \left( i = 2,3, \cdots , r \right) \) という単因子の性質より、 \[ \begin{align} d_k (x) &= e_1 (x) e_2 (x) \cdots e_r (x) \ \ \ \left( k \leq r \right) \end{align}\] が成り立ちます。この式より、 \[ \begin{align} e_k (x) = \frac{d_k (x)}{d_{k-1} (x)} \ \ \ \left( k \leq r \right) \end{align}\] が成り立つため、単因子は行列式因子により定まります。従って、行列式因子の不変性より、単因子は \( A(x) \) により一意的に定まります。
一方、\( k \gt r \) のときは、少なくとも一つは成分がすべて 0 である行および列を選んで小行列式を作ることになるため、 \[ \begin{align} d_k (x) &= 0 \ \ \ \left( k \gt r \right) \end{align}\] となります。よって、行列式因子の不変性より、\( A(x) \) の 0 でない小行列式の最大次数として、\( r \) は \( A(x) \) により一意的に定まります。
以上より、スミス標準形は \( A(x) \) により一意的に定まることが示せました。
3 種類の基本変形の内、行または列の交換を施した場合、交換された行または列を含む小行列式の値は \( -1 \) 倍されます(互換の符号が \( -1 \) であることを思い出してください)。 しかし、これによって \( k \) 次小行列式の最大公約数が変わることはありません。
また、ある行または列に 0 でない複素数 \( c \) をかけた場合、かけられた行または列を含む小行列式の値は \( c \) 倍されますが、これによって \( k \) 次小行列式の最大公約数が変わることもありません。
よって、行または列の交換および、ある行または列に 0 でない複素数 \( c \) をかけるという 2 種類の基本変形については行列式因子を変えないことが示せました。
そこで、残る 1 種類の基本変形、すなわち、 \( A(x) \) の第 \( i \) 行(あるいは列)に第 \( j \) 行(あるいは列) \( \left( i \neq j \right) \) の \( c(x) \) 倍を加える操作について考えます。 この操作で得られる行列を \( A ^{\blacktriangledown} (x) \) とし、\( A ^{\blacktriangledown} (x) \) の \( k \) 次行列式因子を \( d_k ^ {\blacktriangledown} (x)\) とします。 行列式の性質で行に関して成り立つものは列についても成り立つので、以下では行についての操作を考えます。
\( A(x) \) の \( k \) 次小行列式のうち、第 \( i \) 行を含まないものはこの操作では変わりません。 また、第 \( i \) 行と第 \( j \) 行をどちらも含むものもこの操作では変わりません。
そこで、\( A(x) \) の \( k \) 次小行列式 \( \Delta (x) \) が第 \( i \) 行を含み、第 \( j \) 行を含まないとします。 \( \Delta (x) \) と対応する行列 \( A ^{\blacktriangledown} (x) \) における小行列式を \( \Delta ^{\blacktriangledown} (x) \) とします。 また、\( \Delta (x) \) に含まれる \( A(x) \) の第 \( i \) 行を第 \( j \) 行で置き換えたものを \( \Delta _1 (x) \) とします。 すると、次式が成り立ちます。 \[ \begin{align} \Delta ^{\blacktriangledown} (x) = \Delta (x) + c(x) \Delta _1 (x) \end{align}\] \( \Delta (x) \) と \( \Delta _1 (x) \) はいずれも \( A(x) \) の小行列式であるため、これらは \( d_k (x) \) で割り切れます。 従って、\( \Delta ^{\blacktriangledown} (x) \) も \( d_k (x) \) で割り切れます。
以上より、\( A ^{\blacktriangledown} (x) \) のすべての \( k \) 次小行列式は \( d_k (x) \) で割り切れるため、その最大公約数 \( d_k ^ {\blacktriangledown} (x) \) は \( d_k (x) \) で割り切れます。 つまり、 \[ \begin{align} d_k ^ {\blacktriangledown} (x) = d_k (x) q_1 (x) \end{align}\] を満たす \( \mathbb C \)-係数多項式 \( q_1 (x) \) が存在します。
また、基本行列はいずれも正則行列であるため、逆行列が存在します。よって、以上の考察は \( A ^{\blacktriangledown} (x) \) を \( A (x) \) へ移すときにも成り立ちます。 そのため、\( d_k (x) \) は \( d_k ^ {\blacktriangledown} (x) \) で割り切れます。 ゆえに、 \[ \begin{align} d_k (x) = d_k ^ {\blacktriangledown} (x) q_2 (x) \end{align}\] を満たす \( \mathbb C \)-係数多項式 \( q_2 (x) \) が存在します。従って、 \[ \begin{align} d_k (x) &= d_k ^ {\blacktriangledown} (x) q_2 (x) \\\\ &= d_k (x) q_1 (x) q_2 (x) \\\\ q_1 (x) q_2 (x) &= 1 \end{align}\] が成り立ちます。よって、\( q_1 (x) \) と \( q_2 (x) \) はいずれも 0 次多項式、つまり複素数となりますが、\( d_k (x) \) と \( d_k ^ {\blacktriangledown} (x) \) の最高次係数はいずれも 1 であるため、\( q_1 (x) = q_2 (x) = 1 \) が成り立ちます。 よって、\( d_k (x) = d_k ^ {\blacktriangledown} (x) \) が成り立ち、\( n \) 次 \( x \)-行列 \( A(x) \) に基本変形を施したときに、行列式因子が変わらないことが示せました。
それでは、スミス標準形の一意性を証明します。 \( n \) 次 \( x \)-行列 \( A(x) \) およびそのスミス標準形 \( D(x) \) の行列式因子を \( d_1 (x), d_2 (x) , \cdots , d_n (x) \) とします。
まず、\( k \leq r \) のときを考えます。 対角行列の行列式は、その対角成分の積に等しいことを思い出すと、\( D(x) \) の \( k \) 次小行列式は 0 であるか、\( A(x) \) の単因子 \( e_1 (x), e_2 (x) , \cdots , e_r (x) \) から重複なしで任意に選んだ \( k \) 個の積になります。 0 は任意の多項式で割り切れることと、\( e_i (x) \) は \( e_{i-1} (x) \) で割り切れる \( \left( i = 2,3, \cdots , r \right) \) という単因子の性質より、 \[ \begin{align} d_k (x) &= e_1 (x) e_2 (x) \cdots e_r (x) \ \ \ \left( k \leq r \right) \end{align}\] が成り立ちます。この式より、 \[ \begin{align} e_k (x) = \frac{d_k (x)}{d_{k-1} (x)} \ \ \ \left( k \leq r \right) \end{align}\] が成り立つため、単因子は行列式因子により定まります。従って、行列式因子の不変性より、単因子は \( A(x) \) により一意的に定まります。
一方、\( k \gt r \) のときは、少なくとも一つは成分がすべて 0 である行および列を選んで小行列式を作ることになるため、 \[ \begin{align} d_k (x) &= 0 \ \ \ \left( k \gt r \right) \end{align}\] となります。よって、行列式因子の不変性より、\( A(x) \) の 0 でない小行列式の最大次数として、\( r \) は \( A(x) \) により一意的に定まります。
以上より、スミス標準形は \( A(x) \) により一意的に定まることが示せました。
ここまでの議論より、次の 5 つの定理が成り立ちます。
[1] 2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であることは、それらの階数および単因子が一致することの必要十分条件である。
[2] \( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であることは、\( A (x) \) が単位行列に対等であることの必要十分条件である。
[3] 任意の可逆行列は基本行列の積として表される。
[4] 可逆行列は左(右)基本変形のみによって単位行列に変形される。
[5] 2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であることは、 \[ B(x) = P(x) A(x) Q(x) \] となるような二つの可逆行列 \( P(x) \) 、\( Q(x) \) が存在することの必要十分条件である。
[2] \( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であることは、\( A (x) \) が単位行列に対等であることの必要十分条件である。
[3] 任意の可逆行列は基本行列の積として表される。
[4] 可逆行列は左(右)基本変形のみによって単位行列に変形される。
[5] 2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であることは、 \[ B(x) = P(x) A(x) Q(x) \] となるような二つの可逆行列 \( P(x) \) 、\( Q(x) \) が存在することの必要十分条件である。
上の 5 つの定理を順に証明していきます。
[1] の証明
2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であるとします。 \( A(x) \) のスミス標準形を \( A_s (x) \) とすると、何回かの基本変形のみにより \[ B(x) \to A(x) \to A_s(x) \] という変形ができます。ここで、\( \to \) はこの記号の左側の行列から右側の行列へと何回かの基本変形のみにより移れることを意味しています。ゆえに、\( A_s(x) \) は \( B(x) \) のスミス標準形となります。 よって、\( A(x) \) と \( B(x) \) のスミス標準形は一致するため、それらの階数および単因子も一致します。
逆に、\( A(x) \) と \( B(x) \) の階数および単因子が一致しているとします。 この場合、\( A(x) \) と \( B(x) \) のスミス標準形は一致し、これを \( A_s (x) \) とすると、何回かの基本変形のみにより、 \[ B(x) \leftrightarrow A_s(x) \leftrightarrow A(x) \] と変形できるため、\( A(x) \) と \( B(x) \) は対等です。ここで、\( \leftrightarrow \) はこの記号の両側の行列が何回かの基本変形のみにより、互いに移り合うことを意味しています。
[2] の証明
\( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であるとします。 \( | A(x) | \) は \( \mathbb C \) の 0 でない元であるため、\( A(x) \) の \( n \) 次行列式因子 \( d_n (x) \) は 1 となります。 よって、\( A(x) \) の単因子を \( e_1 (x) , e_2 (x) , \cdots , e_n (x) \) とすると、 \[ d_n (x) = e_1 (x) e_2 (x) \cdots e_n (x) = 1\] となります。単因子は最高次係数が 1 の多項式であるため、上の式より \[ e_1 (x) = e_2 (x) = \cdots = e_n (x) = 1\] となり、\( A(x) \) のスミス標準形は単位行列になります。よって、\( A(x) \) は単位行列に対等です。
逆に、\( A(x) \) が単位行列に対等であるとします。\( P(x) \) と \( Q(x) \) をある基本行列の積とすれば、 \[ \begin{align} P(x) A(x) Q(x) &= E \\\\ A(x) &= P(x) ^{-1} Q(x) ^{-1} \\\\ A(x) Q(x) P(x) &= Q(x) P(x) A(x) = E \end{align}\] が成り立ちます。よって、\( A(x) \) は可逆行列であり、逆行列は \( Q(x) P(x) \) となります。
[3] の証明
\( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であるとします。 [2] より \( A(x) \) は単位行列に対等なので、[2] の証明の後半部分より、 \[ \begin{align} A(x) &= P(x) ^{-1} Q(x) ^{-1} \end{align}\] と表すことができます。\( P(x) ^{-1} Q(x) ^{-1} \) は基本行列の積なので、[3] が成り立つと言えます。
[4] については、[2] の証明の後半部分より、 \[ \begin{align} A(x) Q(x) P(x) &= Q(x) P(x) A(x) = E \end{align}\] となるため、成り立ちます。
[5] の証明
2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であるとします。 \( P(x) \) と \( Q(x) \) をある基本行列の積とすれば、 \[ \begin{align} B(x) = P(x) A(x) Q(x) \end{align}\] が成り立ちます。基本行列の積は可逆行列です。
逆に、二つの可逆行列 \( P(x) \) 、\( Q(x) \) が存在し、 \[ \begin{align} B(x) = P(x) A(x) Q(x) \end{align}\] を満たすとします。[3] より、\( P(x) \) と \( Q(x) \) は基本行列の積として表すことができるため、\( A(x) \) と \( B(x) \) は対等です。
[1] の証明
2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であるとします。 \( A(x) \) のスミス標準形を \( A_s (x) \) とすると、何回かの基本変形のみにより \[ B(x) \to A(x) \to A_s(x) \] という変形ができます。ここで、\( \to \) はこの記号の左側の行列から右側の行列へと何回かの基本変形のみにより移れることを意味しています。ゆえに、\( A_s(x) \) は \( B(x) \) のスミス標準形となります。 よって、\( A(x) \) と \( B(x) \) のスミス標準形は一致するため、それらの階数および単因子も一致します。
逆に、\( A(x) \) と \( B(x) \) の階数および単因子が一致しているとします。 この場合、\( A(x) \) と \( B(x) \) のスミス標準形は一致し、これを \( A_s (x) \) とすると、何回かの基本変形のみにより、 \[ B(x) \leftrightarrow A_s(x) \leftrightarrow A(x) \] と変形できるため、\( A(x) \) と \( B(x) \) は対等です。ここで、\( \leftrightarrow \) はこの記号の両側の行列が何回かの基本変形のみにより、互いに移り合うことを意味しています。
[2] の証明
\( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であるとします。 \( | A(x) | \) は \( \mathbb C \) の 0 でない元であるため、\( A(x) \) の \( n \) 次行列式因子 \( d_n (x) \) は 1 となります。 よって、\( A(x) \) の単因子を \( e_1 (x) , e_2 (x) , \cdots , e_n (x) \) とすると、 \[ d_n (x) = e_1 (x) e_2 (x) \cdots e_n (x) = 1\] となります。単因子は最高次係数が 1 の多項式であるため、上の式より \[ e_1 (x) = e_2 (x) = \cdots = e_n (x) = 1\] となり、\( A(x) \) のスミス標準形は単位行列になります。よって、\( A(x) \) は単位行列に対等です。
逆に、\( A(x) \) が単位行列に対等であるとします。\( P(x) \) と \( Q(x) \) をある基本行列の積とすれば、 \[ \begin{align} P(x) A(x) Q(x) &= E \\\\ A(x) &= P(x) ^{-1} Q(x) ^{-1} \\\\ A(x) Q(x) P(x) &= Q(x) P(x) A(x) = E \end{align}\] が成り立ちます。よって、\( A(x) \) は可逆行列であり、逆行列は \( Q(x) P(x) \) となります。
[3] の証明
\( n \) 次 \( x \)-行列 \( A(x) \) が可逆行列であるとします。 [2] より \( A(x) \) は単位行列に対等なので、[2] の証明の後半部分より、 \[ \begin{align} A(x) &= P(x) ^{-1} Q(x) ^{-1} \end{align}\] と表すことができます。\( P(x) ^{-1} Q(x) ^{-1} \) は基本行列の積なので、[3] が成り立つと言えます。
[4] については、[2] の証明の後半部分より、 \[ \begin{align} A(x) Q(x) P(x) &= Q(x) P(x) A(x) = E \end{align}\] となるため、成り立ちます。
[5] の証明
2 つの \( n \) 次 \( x \)-行列 \( A(x) \) と \( B(x) \) が対等であるとします。 \( P(x) \) と \( Q(x) \) をある基本行列の積とすれば、 \[ \begin{align} B(x) = P(x) A(x) Q(x) \end{align}\] が成り立ちます。基本行列の積は可逆行列です。
逆に、二つの可逆行列 \( P(x) \) 、\( Q(x) \) が存在し、 \[ \begin{align} B(x) = P(x) A(x) Q(x) \end{align}\] を満たすとします。[3] より、\( P(x) \) と \( Q(x) \) は基本行列の積として表すことができるため、\( A(x) \) と \( B(x) \) は対等です。
\( n \) 次 \( x \)-行列の商と余り
\( n \) 次 \( x \)-行列を \( x \) の多項式のようにみなして、
\[ \begin{align}
A(x) = A_0 + A_1 x + \cdots + A_k x^k, \ A_k \neq 0
\end{align}\]
と表すとします。
ここで、\( A_0, A_1, \cdots , A_k \) は \( \mathbb C \) の元を成分とする行列とします。
また、\( k \) を \( A(x) \) のべき次数と呼びます。
以上の条件のもとで、次の定理が成り立ちます。
以上の条件のもとで、次の定理が成り立ちます。
\[ \begin{align}
n \ \text{次} \ x \text{-行列における商と余り}
\end{align}\]
二つの \( n \) 次 \( x \)-行列、
\[ \begin{align}
A(x) &= A_0 + A_1 x + \cdots + A_k x^k, \ A_k \neq 0 \ \ldots (1) \\\\
B(x) &= B_0 + B_1 x + \cdots + B_l x^{l}, \ B_l \neq 0 \ \ldots (2)
\end{align}\]
において、\( B(x) \) の最高次係数行列 \( B_l \) が正則なら、
\[ \begin{align}
A(x) = B(x) Q_1(x) + R_1 (x) \ \ldots (3)
\end{align}\]
を満たす二つの \( n \) 次 \( x \)-行列 \( Q_1 (x) \) 、\( R_1 (x) \) がただ一組存在する。
ただし、\( R_1 (x) \) は零行列であるか、またはそのべき次数が \( B(x) \) のべき次数よりも小さい。
また、 \[ \begin{align} A(x) = Q_2(x) B(x) + R_2 (x) \ \ldots (4) \end{align}\] を満たす二つの \( n \) 次 \( x \)-行列 \( Q_2 (x) \) 、\( R_2 (x) \) がただ一組存在する。 ただし、\( R_2 (x) \) は零行列であるか、またはそのべき次数が \( B(x) \) のべき次数よりも小さい。
また、 \[ \begin{align} A(x) = Q_2(x) B(x) + R_2 (x) \ \ldots (4) \end{align}\] を満たす二つの \( n \) 次 \( x \)-行列 \( Q_2 (x) \) 、\( R_2 (x) \) がただ一組存在する。 ただし、\( R_2 (x) \) は零行列であるか、またはそのべき次数が \( B(x) \) のべき次数よりも小さい。
まず、\( A(x) \) のべき次数 \( k \) についての数学的帰納法により、\( (3) \) 式を満たす \( Q_1 (x) \) と \( R_1 (x) \) の存在を証明します。
[1] \( k = 0 \) のとき
\( l \gt 0 \) なら、\( Q_1 (x) = O \) 、\( R_1 (x) = A(x) = A_0 \) と置けばよいです。 \( l=0 \) なら、\( B(x) = B_0 \) なので、\( Q_1 (x) = B_0 ^{-1} A(x) \) 、\( R_1 (x) = O \) と置けばよいです。
[2] \( k = n + 1 \) とし、\( k \leq n \) を満たすすべての \( k \) について定理が成り立つと仮定
\( n + 1 \lt l \) なら、\( Q_1 (x) = O \) 、\( R_1 (x) = A(x) \) と置けばよいです。
\( n + 1 \geq l \) の場合、 \[ \begin{align} A ^ {\Diamond} (x) = A(x) - B(x) B_l ^{-1} A_{n+1} x^{n+1-l} \end{align}\] とします。すると、 \[ \begin{align} A ^ {\Diamond} (x) &= A(x) - \left( B_0 + B_1 x + \cdots + B_l x^{l} \right) B_l ^{-1} A_{n+1} x^{n+1-l} \\\\ &= A(x) - \left\{ \left( B_0 + B_1 x + \cdots + B_{l-1} x^{l-1} \right) B_l ^{-1} A_{n+1} x^{n+1-l} + A_{n+1} x^{n+1} \right\} \end{align}\] となるため、\( A ^ {\Diamond} (x) \) のべき次数は \( n \) 以下となります。 よって、仮定より、 \[ \begin{align} A ^ {\Diamond} (x) = B(x) Q ^ {\Diamond} (x) + R_1 (x) \end{align}\] がを満たす \( Q ^ {\Diamond} (x) \) および \( R_1 (x) \) が存在します。 ただし、\( R_1 (x) \) は零行列であるか、そのべき指数が \( l \) より小さいとします。 そこで、 \[ \begin{align} Q_1 (x) = B_l ^{-1} A_{n+1} x^{n+1-l} + Q ^ {\Diamond} (x) \end{align}\] とおくと、 \[ \begin{align} B(x) Q_1 (x) + R_1 (x) &= B(x) \left\{ B_l ^{-1} A_{n+1} x^{n+1-l} + Q ^ {\Diamond} (x) \right\} + R_1 (x) \\\\ &= B(x) B_l ^{-1} A_{n+1} x^{n+1-l} + B(x) Q ^ {\Diamond} (x) + R_1 (x) \\\\ &= B(x) B_l ^{-1} A_{n+1} x^{n+1-l} + A ^ {\Diamond} (x) \\\\ &= B(x) B_l ^{-1} A_{n+1} x^{n+1-l} + A(x) - B(x) B_l ^{-1} A_{n+1} x^{n+1-l} \\\\ &= A(x) \end{align}\] が成り立ちます。 よって、\( k = n+1 \) のときも \( (3) \) 式を満たす \( Q_1 (x) \) と \( R_1 (x) \) が存在します。
[1] と [2] より、すべての \( k \) について、\( (3) \) 式を満たす \( Q_1 (x) \) と \( R_1 (x) \) が存在します。
続いて、一意性を示します。もう一組の \( Q_1 ^{\blacktriangle} (x) \) 、\( R_1 ^{\blacktriangle} (x) \) が条件を満たすとすると、 \[ \begin{align} B (x) Q_1 (x) + R_1 (x) &= B(x) Q_1 ^{\blacktriangle} (x) + R_1 ^{\blacktriangle} (x) \\\\ B(x) \left\{ Q_1 (x) - Q_1 ^{\blacktriangle} (x) \right\} &= R_1 ^{\blacktriangle} (x) - R_1 (x) \end{align}\] となります。 もし、\( Q_1 (x) \neq Q_1 ^{\blacktriangle} (x) \) であれば、左辺のべき次数は \( B(x) \) のべき次数以上となります。 一方、\( R_1 (x) \) と \( R_1 ^{\blacktriangle} (x) \) はいずれもそのべき次数が \( B(x) \) のべき次数より小さいため、右辺のべき次数も \( B(x) \) のべき次数より小さくなりますが、これは右辺と左辺のべき次数が一致しないことを示します。 よって、\( Q_1 (x) = Q_1 ^{\blacktriangle} (x) \) であり、左辺が \( O \) となるため、\( R_1 (x) = R_1 ^{\blacktriangle} (x) \) も成り立ちます。
\( (4) \) 式を満たすただ一組の \( Q_2 (x) \) と \( R_2 (x) \) の存在も同様に証明されます。
[1] \( k = 0 \) のとき
\( l \gt 0 \) なら、\( Q_1 (x) = O \) 、\( R_1 (x) = A(x) = A_0 \) と置けばよいです。 \( l=0 \) なら、\( B(x) = B_0 \) なので、\( Q_1 (x) = B_0 ^{-1} A(x) \) 、\( R_1 (x) = O \) と置けばよいです。
[2] \( k = n + 1 \) とし、\( k \leq n \) を満たすすべての \( k \) について定理が成り立つと仮定
\( n + 1 \lt l \) なら、\( Q_1 (x) = O \) 、\( R_1 (x) = A(x) \) と置けばよいです。
\( n + 1 \geq l \) の場合、 \[ \begin{align} A ^ {\Diamond} (x) = A(x) - B(x) B_l ^{-1} A_{n+1} x^{n+1-l} \end{align}\] とします。すると、 \[ \begin{align} A ^ {\Diamond} (x) &= A(x) - \left( B_0 + B_1 x + \cdots + B_l x^{l} \right) B_l ^{-1} A_{n+1} x^{n+1-l} \\\\ &= A(x) - \left\{ \left( B_0 + B_1 x + \cdots + B_{l-1} x^{l-1} \right) B_l ^{-1} A_{n+1} x^{n+1-l} + A_{n+1} x^{n+1} \right\} \end{align}\] となるため、\( A ^ {\Diamond} (x) \) のべき次数は \( n \) 以下となります。 よって、仮定より、 \[ \begin{align} A ^ {\Diamond} (x) = B(x) Q ^ {\Diamond} (x) + R_1 (x) \end{align}\] がを満たす \( Q ^ {\Diamond} (x) \) および \( R_1 (x) \) が存在します。 ただし、\( R_1 (x) \) は零行列であるか、そのべき指数が \( l \) より小さいとします。 そこで、 \[ \begin{align} Q_1 (x) = B_l ^{-1} A_{n+1} x^{n+1-l} + Q ^ {\Diamond} (x) \end{align}\] とおくと、 \[ \begin{align} B(x) Q_1 (x) + R_1 (x) &= B(x) \left\{ B_l ^{-1} A_{n+1} x^{n+1-l} + Q ^ {\Diamond} (x) \right\} + R_1 (x) \\\\ &= B(x) B_l ^{-1} A_{n+1} x^{n+1-l} + B(x) Q ^ {\Diamond} (x) + R_1 (x) \\\\ &= B(x) B_l ^{-1} A_{n+1} x^{n+1-l} + A ^ {\Diamond} (x) \\\\ &= B(x) B_l ^{-1} A_{n+1} x^{n+1-l} + A(x) - B(x) B_l ^{-1} A_{n+1} x^{n+1-l} \\\\ &= A(x) \end{align}\] が成り立ちます。 よって、\( k = n+1 \) のときも \( (3) \) 式を満たす \( Q_1 (x) \) と \( R_1 (x) \) が存在します。
[1] と [2] より、すべての \( k \) について、\( (3) \) 式を満たす \( Q_1 (x) \) と \( R_1 (x) \) が存在します。
続いて、一意性を示します。もう一組の \( Q_1 ^{\blacktriangle} (x) \) 、\( R_1 ^{\blacktriangle} (x) \) が条件を満たすとすると、 \[ \begin{align} B (x) Q_1 (x) + R_1 (x) &= B(x) Q_1 ^{\blacktriangle} (x) + R_1 ^{\blacktriangle} (x) \\\\ B(x) \left\{ Q_1 (x) - Q_1 ^{\blacktriangle} (x) \right\} &= R_1 ^{\blacktriangle} (x) - R_1 (x) \end{align}\] となります。 もし、\( Q_1 (x) \neq Q_1 ^{\blacktriangle} (x) \) であれば、左辺のべき次数は \( B(x) \) のべき次数以上となります。 一方、\( R_1 (x) \) と \( R_1 ^{\blacktriangle} (x) \) はいずれもそのべき次数が \( B(x) \) のべき次数より小さいため、右辺のべき次数も \( B(x) \) のべき次数より小さくなりますが、これは右辺と左辺のべき次数が一致しないことを示します。 よって、\( Q_1 (x) = Q_1 ^{\blacktriangle} (x) \) であり、左辺が \( O \) となるため、\( R_1 (x) = R_1 ^{\blacktriangle} (x) \) も成り立ちます。
\( (4) \) 式を満たすただ一組の \( Q_2 (x) \) と \( R_2 (x) \) の存在も同様に証明されます。
特性 \( x \)-行列
\( \mathbb C \) の元を成分とする \( n \) 次行列 \( A \) に対し、\( n \) 次 \( x \)-行列 \( xE - A \) を \( A \) の特性 \( x
\)-行列と言います。
特性 \( x \)-行列について、次の定理が成り立ちます。
\[ \text{特性} \ x \text{-行列による相似判定定理} \]
\( \mathbb C \) の元を成分とする二つの \( n \) 次行列 \( A \) と \( B \) について、\( B = P^{-1} A P \) となる正則行列 \( P \)
が存在することは、それらの特性 \( x \)-行列 \( xE - A \) 、\( xE - B \) が対等であることの必要十分条件である。
\( B = P^{-1} A P \) が成り立つとすると、
\[ \begin{align}
xE - B &= xE - P^{-1} A P \\\\
&= P^{-1} \left( xE - A \right) P
\end{align}\]
となります。\( P \) は可逆行列であり、これは基本行列の積として表されます。
よって、\( xE - A \) と \( xE - B \) は対等です。
逆に、\( xE - A \) と \( xE - B \) が対等であるとすると、 \[ \begin{align} \left( xE - A \right) P(x) = Q(x) \left( xE - B \right) \ \ldots (5) \end{align}\] となる可逆行列 \( P(x) \) 、\( Q(x) \) が存在します。 \( xE - A \) と \( xE - B \) の最高次係数行列はいずれも \( E \) であり、これは正則です。 また、これらのべき次数はいずれも 1 です。よって、\( n \) 次 \( x \)-行列における商と余りの定理より、 \[ \begin{align} P(x) &= P_1 (x) \left( xE - B \right) + P \\\\ Q(x) &= \left( xE - A \right) Q_1 (x) + Q \end{align}\] を満たす \( x \)-行列 \( P_1 (x) \) 、\( Q_1 (x) \) 、および、\( \mathbb C \) の元を成分とする二つの \( n \) 次行列 \( P \) と \( Q \) が存在します。 これらを、\( (5) \) 式に代入すると、 \[ \begin{align} \left( xE - A \right) \left\{ P_1 (x) \left( xE - B \right) + P \right\} &= \left\{ \left( xE - A \right) Q_1 (x) + Q \right\} \left( xE - B \right) \\\\ \left( xE - A \right) \left\{ P_1 (x) - Q_1 (x) \right\} \left( xE - B \right) &= Q \left( xE - B \right) - \left( xE - A \right) P \ \ldots (6) \end{align}\] \( P_1 (x) \neq Q_1(x) \) の場合、\( (6) \) 式の左辺のべき次数は 2 以上、右辺のべき次数は 1 以下であるか、次数なしのため、両辺のべき次数は一致しません。 よって、\( P_1 (x) = Q_1(x) \) が成り立ち、従って、 \[ \begin{align} Q \left( xE - B \right) &= \left( xE - A \right) P \\\\ \left( P - Q \right) x &= AP - QB \end{align}\] も成り立ちます。上の式において、\( P \neq Q \) とすると、左辺のべき次数は 1 、右辺のべき次数は 0 となり、両辺のべき次数が一致しません。 よって、次が成り立ちます。 \[ \begin{align} P = Q, \ AP=QB=PB \ \ldots (7) \end{align}\] 続いて、\( P \) が正則であることを示します。 \( P(x) \) は可逆行列であるため、\( P (x) ^{-1}\) が存在し、\( n \) 次 \( x \)-行列における商と余りの定理より、 \[ \begin{align} P(x)^{-1} &= R(x) \left( xE - A \right) + R \end{align}\] を満たす \( x \)-行列 \( R (x) \) 、および、\( \mathbb C \) の元を成分とする \( n \) 次行列 \( R \) が存在します。 よって、 \[ \begin{align} E &= P(x)^{-1} P(x) \\\\ &= \left\{ R(x) \left( xE - A \right) + R \right\} \left\{ P_1 (x) \left( xE - B \right) + P \right\} \\\\ &= \left\{ R(x) \left( xE - A \right) + R \right\} P_1 (x) \left( xE - B \right) + R(x) \left( xE - A \right) P + RP \\\\ &= \left\{ R(x) \left( xE - A \right) + R \right\} P_1 (x) \left( xE - B \right) + R(x) Q \left( xE - B \right) + RP \\\\ &= \left[ \left\{ R(x) \left( xE - A \right) + R \right\} P_1 (x) + R(x) Q \right] \left( xE - B \right) + RP \\\\ \end{align}\] 右辺第 1 項の \( [\ ] \) 内が零行列でない場合、右辺のべき次数は 1 以上になります。 一方、左辺のべき次数は 0 なので、右辺第 1 項の \( [\ ] \) 内は零行列であり、\( RP=E \) となります。 よって、\( P \) には左逆行列 \( R \) が存在するので、\( P \) は正則行列です。 従って、\( (7) \) 式より、\( B = P^{-1} A P \) が成り立ちます。
逆に、\( xE - A \) と \( xE - B \) が対等であるとすると、 \[ \begin{align} \left( xE - A \right) P(x) = Q(x) \left( xE - B \right) \ \ldots (5) \end{align}\] となる可逆行列 \( P(x) \) 、\( Q(x) \) が存在します。 \( xE - A \) と \( xE - B \) の最高次係数行列はいずれも \( E \) であり、これは正則です。 また、これらのべき次数はいずれも 1 です。よって、\( n \) 次 \( x \)-行列における商と余りの定理より、 \[ \begin{align} P(x) &= P_1 (x) \left( xE - B \right) + P \\\\ Q(x) &= \left( xE - A \right) Q_1 (x) + Q \end{align}\] を満たす \( x \)-行列 \( P_1 (x) \) 、\( Q_1 (x) \) 、および、\( \mathbb C \) の元を成分とする二つの \( n \) 次行列 \( P \) と \( Q \) が存在します。 これらを、\( (5) \) 式に代入すると、 \[ \begin{align} \left( xE - A \right) \left\{ P_1 (x) \left( xE - B \right) + P \right\} &= \left\{ \left( xE - A \right) Q_1 (x) + Q \right\} \left( xE - B \right) \\\\ \left( xE - A \right) \left\{ P_1 (x) - Q_1 (x) \right\} \left( xE - B \right) &= Q \left( xE - B \right) - \left( xE - A \right) P \ \ldots (6) \end{align}\] \( P_1 (x) \neq Q_1(x) \) の場合、\( (6) \) 式の左辺のべき次数は 2 以上、右辺のべき次数は 1 以下であるか、次数なしのため、両辺のべき次数は一致しません。 よって、\( P_1 (x) = Q_1(x) \) が成り立ち、従って、 \[ \begin{align} Q \left( xE - B \right) &= \left( xE - A \right) P \\\\ \left( P - Q \right) x &= AP - QB \end{align}\] も成り立ちます。上の式において、\( P \neq Q \) とすると、左辺のべき次数は 1 、右辺のべき次数は 0 となり、両辺のべき次数が一致しません。 よって、次が成り立ちます。 \[ \begin{align} P = Q, \ AP=QB=PB \ \ldots (7) \end{align}\] 続いて、\( P \) が正則であることを示します。 \( P(x) \) は可逆行列であるため、\( P (x) ^{-1}\) が存在し、\( n \) 次 \( x \)-行列における商と余りの定理より、 \[ \begin{align} P(x)^{-1} &= R(x) \left( xE - A \right) + R \end{align}\] を満たす \( x \)-行列 \( R (x) \) 、および、\( \mathbb C \) の元を成分とする \( n \) 次行列 \( R \) が存在します。 よって、 \[ \begin{align} E &= P(x)^{-1} P(x) \\\\ &= \left\{ R(x) \left( xE - A \right) + R \right\} \left\{ P_1 (x) \left( xE - B \right) + P \right\} \\\\ &= \left\{ R(x) \left( xE - A \right) + R \right\} P_1 (x) \left( xE - B \right) + R(x) \left( xE - A \right) P + RP \\\\ &= \left\{ R(x) \left( xE - A \right) + R \right\} P_1 (x) \left( xE - B \right) + R(x) Q \left( xE - B \right) + RP \\\\ &= \left[ \left\{ R(x) \left( xE - A \right) + R \right\} P_1 (x) + R(x) Q \right] \left( xE - B \right) + RP \\\\ \end{align}\] 右辺第 1 項の \( [\ ] \) 内が零行列でない場合、右辺のべき次数は 1 以上になります。 一方、左辺のべき次数は 0 なので、右辺第 1 項の \( [\ ] \) 内は零行列であり、\( RP=E \) となります。 よって、\( P \) には左逆行列 \( R \) が存在するので、\( P \) は正則行列です。 従って、\( (7) \) 式より、\( B = P^{-1} A P \) が成り立ちます。
おわりに、スミス標準形に名を残しているヘンリー・ジョン・スティーブン・スミスは19世紀に活躍したイギリスの数学者です。
スミス標準形以外にも、数論やリーマン積分の分野に業績を残しています。

ヘンリー・ジョン・スティーブン・スミス(1826-1883)
参考:
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行
[2] Wikipedia Henry John Stephen Smith、https://en.wikipedia.org/wiki/Henry_John_Stephen_Smith、2025年4月10日閲覧