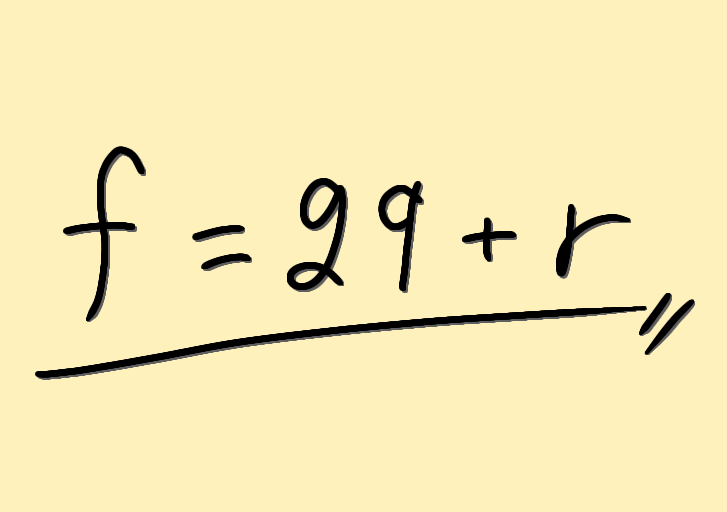
目次
・一変数多項式
・多項式の割り算
・公約数
一変数多項式
\[ 一変数多項式\]
複素数全体の集合を \( \mathbb C \) と表す。1 つの文字 \( x \) と、\( \mathbb C \) の元 \( a_0 , a_1 , \cdots , a_n \)
により作られる次の式を、文字 \( x \) の \( \mathbb C \) -係数多項式と呼ぶ。
\[ \sum _{i=0} ^n a_i x^i = a_0 + a_1 x + \cdots + a_n x^n \]
上の定義では、多項式の係数は複素数であるとしましたが、係数を実数全体の集合 \( \mathbb R \) の元に限るなら、その多項式は \( \mathbb R \) -係数多項式と呼ばれます。
以下では、多項式の係数は複素数全体 \( \mathbb C \) の元とします。
2 つの多項式 \[ \begin{align} f \left( x \right) = \sum _{i=0} ^n a_i x^i , \ \ g \left( x \right) = \sum _{i=0} ^n b_i x^i \end{align}\] について、 \[ \begin{align} a_i = b_i \ \ \left( i = 0, 1, \cdots , n \right) \end{align}\] が成り立つとき、\( f \left( x \right) \) と \( g \left( x \right) \) は等しいと言い、\( f \left( x \right) = g \left( x \right) \) と表します。 また、多項式同士の和 \( f \left( x \right) + g \left( x \right) \) と積 \( f \left( x \right) g \left( x \right) \) を \[ \begin{align} & f \left( x \right) + g \left( x \right) = \sum _{i=0} ^n \left( a_i + b_i \right) x^i \\\\ & f \left( x \right) g \left( x \right) = \sum _{i=0} ^{2n} c_i x^i , \ \ c_i = \sum _{j+k=i} a_j b_k \ \ \left( 0 \leq j \leq n \ \rm かつ \ 0 \leq \it k \rm \leq \it n \rm \right) \end{align}\] により定義します。これにより、\( \mathbb C \) -係数多項式全体の集合の中では加法、減法、乗法がいつでも行えて、結合法則、分配法則、交換法則も成り立ちます。
多項式 \( f \left( x \right) = \sum _{i=0} ^n a_i x^i \) において、\( x \) に複素数 \( \alpha \) を代入して得られる複素数 \( \sum _{i=0} ^n a_i \alpha ^i \) を、\( f \left( x \right) \) の \( \alpha \) での値と呼び、\( f \left( \alpha \right) \) で表します。
2 つの多項式 \[ \begin{align} f \left( x \right) = \sum _{i=0} ^n a_i x^i , \ \ g \left( x \right) = \sum _{i=0} ^n b_i x^i \end{align}\] について、 \[ \begin{align} a_i = b_i \ \ \left( i = 0, 1, \cdots , n \right) \end{align}\] が成り立つとき、\( f \left( x \right) \) と \( g \left( x \right) \) は等しいと言い、\( f \left( x \right) = g \left( x \right) \) と表します。 また、多項式同士の和 \( f \left( x \right) + g \left( x \right) \) と積 \( f \left( x \right) g \left( x \right) \) を \[ \begin{align} & f \left( x \right) + g \left( x \right) = \sum _{i=0} ^n \left( a_i + b_i \right) x^i \\\\ & f \left( x \right) g \left( x \right) = \sum _{i=0} ^{2n} c_i x^i , \ \ c_i = \sum _{j+k=i} a_j b_k \ \ \left( 0 \leq j \leq n \ \rm かつ \ 0 \leq \it k \rm \leq \it n \rm \right) \end{align}\] により定義します。これにより、\( \mathbb C \) -係数多項式全体の集合の中では加法、減法、乗法がいつでも行えて、結合法則、分配法則、交換法則も成り立ちます。
多項式 \( f \left( x \right) = \sum _{i=0} ^n a_i x^i \) において、\( x \) に複素数 \( \alpha \) を代入して得られる複素数 \( \sum _{i=0} ^n a_i \alpha ^i \) を、\( f \left( x \right) \) の \( \alpha \) での値と呼び、\( f \left( \alpha \right) \) で表します。
\( a_n \neq 0 \) のとき、\( n \) を多項式 \( f(x) \) の次数と言います。
ただし、\( \mathbb C \) の元 0 については次数を持たないものとします。
0 でない多項式 \( f(x) \) の次数を \( \rm deg \ \it f \rm \left( \it x \rm \right) \) と表すと、次式が成り立ちます。
\[ \begin{align}
& \rm deg \ \left( \it f \rm \left( \it x \rm \right) + \it g \rm \left( \it x \rm \right) \right) \leq
\max \left\{ \rm deg \ \it f \rm \left( \it x \rm \right) , \rm deg \ \it g \rm \left( \it x \rm \right)
\right\} \\\\
& \rm deg \ \left( \it f \rm \left( \it x \rm \right) \it g \rm \left( \it x \rm \right) \right) = \rm
deg \ \it f \rm \left( \it x \rm \right) + \rm deg \ \it g \rm \left( \it x \rm \right)
\end{align}\]
ここで、\( \max \left\{ X,Y \right\} \) は \( X \) と \( Y \) の大きい方の値を意味します。
多項式の割り算
\( \mathbb C \) -係数多項式 \( f(x) \) 、\( g(x) \) に対して、
\[ \begin{align}
f(x) = g(x)q(x)
\end{align}\]
となる \( \mathbb C \) -係数多項式 \( q(x) \) が存在するとき、\( f(x) \) は \( g(x) \) で割り切れる、または \( g(x) \) は \( f(x)
\) を割り切ると言います。
また、\( g(x) \) を \( f(x) \) の約数、\( f(x) \) を \( g(x) \) の倍数と呼びます。
\( f(x) \) の約数が \( f(x) \) の定数倍および 0 次多項式のみのとき、\( f(x) \) は既約であると言います。
多項式同士の割り算について、次の定理が成り立ちます。
\( f(x) \) の約数が \( f(x) \) の定数倍および 0 次多項式のみのとき、\( f(x) \) は既約であると言います。
多項式同士の割り算について、次の定理が成り立ちます。
\[ 商と余り \]
\( f(x) \) を \( \mathbb C \) -係数多項式、\( g(x) \) を 0 でない \( \mathbb C \) -係数多項式とする。
このとき、
\[ f(x) = g(x)q(x) + r(x) \]
となる \( \mathbb C \) -係数多項式 \( q(x) \) および \( r(x) \) がただ一組存在する。
ただし、\( r(x) \) は 0 であるか、あるいは \( g(x) \) より低次の多項式である。
なお、\( q(x) \) を、\( f(x) \) を \( g(x) \) で割ったときの商と呼び、\( r(x) \) を余りと呼ぶ。
まず、商と余りの一意性を示します。
\( q_1 (x) \) 、\( r_1 (x) \) および \( q_2 (x) \) 、\( r_2 (x) \) がともに上の定理の条件を満たすならば、
\[ \begin{align}
g(x) q_1 (x) + r_1 (x) = g(x) q_2 (x) + r_2 (x)
\end{align}\]
よって、
\[ \begin{align}
g(x) \left( q_1 (x) - q_2 (x) \right) = r_2 (x) - r_1 (x)
\end{align}\]
が成り立ちます。
もし、\( q_1 (x) \neq q_2 (x) \) なら、左辺の次数は \( \rm deg \it \ g \rm( \it x \rm ) \) 以上になります。
ところが、\( r_1 (x) \) と \( r_2 (x) \) はいずれも \( g(x) \) より低次の多項式であるため、右辺の次数は \( \rm deg \it \ g \rm( \it x \rm )
\) より小さいです。
よって、\( q_1 (x) = q_2 (x) \) となり、これにより \( r_1 (x) = r_2 (x) \) が成り立ちます。
続いて、定理の条件を満たす \( q(x) \) と \( r(x) \) の存在を示します。 もし、\( f(x) = 0 \) であるなら、\( q(x) = r(x) = 0 \) とすれば条件を満たします。 そこで、\( f(x) \neq 0 \) とし、\( \rm deg \it \ f \rm( \it x \rm ) \) についての数学的帰納法を使って証明していきます。
[1] \( \rm deg \it \ f \rm( \it x \rm ) = 0 \) のとき
\( \rm deg \it \ g \rm( \it x \rm ) = 0 \) なら、\( q(x) = f(x) / g(x) \) 、\( r(x) = 0 \) とすれば条件を満たします。 \( \rm deg \it \ g \rm( \it x \rm ) \gt 0 \) なら、\( q(x) = 0 \) 、\( r(x) = f(x) \) とすればよいです。
[2] \( \rm deg \it \ f \rm( \it x \rm ) = \it n \rm + 1 \) とし、\( n \) 次以下の多項式 \( f(x) \) に対して定理が成り立つと仮定 \[ \begin{align} f(x) &= a_{n+1} x^{n+1} + a_n x^{n} + \cdots + a_1 x + a_{0} , \ \ a_{n+1} \neq 0 \\\\ g(x) &= b_{m+1} x^{m+1} + b_m x^{m} + \cdots + b_1 x + b_{0} , \ \ b_{m+1} \neq 0 \end{align}\] とします。\( n \lt m \) なら、\( q(x) = 0 \) 、\( r(x) = f(x) \) とすればよいです。
\( n \geq m \) なら、 \[ \begin{align} f_1 (x) = f(x) - \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) \end{align}\] とすると、\( f_1 (x) \) は \( n \) 次以下の多項式です。そのため、数学的帰納法の仮定より、 \[ \begin{align} f_1 (x) = g(x)q_1 (x) + r(x) \end{align}\] を満たす多項式 \( q_1 (x) \) および \( m \) 次以下の多項式、または 0 となる \( r(x) \) が存在します。 そこで、 \[ \begin{align} q(x) = \frac{a_{n+1}}{b_{m+1}} x^{n-m} + q_1 (x) \end{align}\] とすると、 \[ \begin{align} g(x) q(x) + r(x) &= g(x) \left( \frac{a_{n+1}}{b_{m+1}} x^{n-m} + q_1 (x) \right) + r(x) \\\\ &= \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) + g(x) q_1 (x) + r(x) \\\\ &= \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) + f_1 (x) \\\\ &= \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) + f(x) - \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) \\\\ &= f(x) \end{align}\] となり、上の定理が成り立ちます。
[1] と [2] より、\( f(x) \neq 0 \) のときも上の定理が成り立つことが示せました。 よって、任意の多項式 \( f(x) \) について上の定理は成り立つと言えます。
上の定理からただちに次の定理が従います。
続いて、定理の条件を満たす \( q(x) \) と \( r(x) \) の存在を示します。 もし、\( f(x) = 0 \) であるなら、\( q(x) = r(x) = 0 \) とすれば条件を満たします。 そこで、\( f(x) \neq 0 \) とし、\( \rm deg \it \ f \rm( \it x \rm ) \) についての数学的帰納法を使って証明していきます。
[1] \( \rm deg \it \ f \rm( \it x \rm ) = 0 \) のとき
\( \rm deg \it \ g \rm( \it x \rm ) = 0 \) なら、\( q(x) = f(x) / g(x) \) 、\( r(x) = 0 \) とすれば条件を満たします。 \( \rm deg \it \ g \rm( \it x \rm ) \gt 0 \) なら、\( q(x) = 0 \) 、\( r(x) = f(x) \) とすればよいです。
[2] \( \rm deg \it \ f \rm( \it x \rm ) = \it n \rm + 1 \) とし、\( n \) 次以下の多項式 \( f(x) \) に対して定理が成り立つと仮定 \[ \begin{align} f(x) &= a_{n+1} x^{n+1} + a_n x^{n} + \cdots + a_1 x + a_{0} , \ \ a_{n+1} \neq 0 \\\\ g(x) &= b_{m+1} x^{m+1} + b_m x^{m} + \cdots + b_1 x + b_{0} , \ \ b_{m+1} \neq 0 \end{align}\] とします。\( n \lt m \) なら、\( q(x) = 0 \) 、\( r(x) = f(x) \) とすればよいです。
\( n \geq m \) なら、 \[ \begin{align} f_1 (x) = f(x) - \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) \end{align}\] とすると、\( f_1 (x) \) は \( n \) 次以下の多項式です。そのため、数学的帰納法の仮定より、 \[ \begin{align} f_1 (x) = g(x)q_1 (x) + r(x) \end{align}\] を満たす多項式 \( q_1 (x) \) および \( m \) 次以下の多項式、または 0 となる \( r(x) \) が存在します。 そこで、 \[ \begin{align} q(x) = \frac{a_{n+1}}{b_{m+1}} x^{n-m} + q_1 (x) \end{align}\] とすると、 \[ \begin{align} g(x) q(x) + r(x) &= g(x) \left( \frac{a_{n+1}}{b_{m+1}} x^{n-m} + q_1 (x) \right) + r(x) \\\\ &= \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) + g(x) q_1 (x) + r(x) \\\\ &= \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) + f_1 (x) \\\\ &= \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) + f(x) - \frac{a_{n+1}}{b_{m+1}} x^{n-m} g(x) \\\\ &= f(x) \end{align}\] となり、上の定理が成り立ちます。
[1] と [2] より、\( f(x) \neq 0 \) のときも上の定理が成り立つことが示せました。 よって、任意の多項式 \( f(x) \) について上の定理は成り立つと言えます。
上の定理からただちに次の定理が従います。
\[ \begin{align}
剰余定理
\end{align}\]
\( f(x) \) を \( x- \alpha \ \left( \alpha \in \mathbb C \right) \) で割ったときの余りは \( f \left( \alpha
\right) \) である。
公約数
\( h(x) \) が \( f_1 (x), f_2 (x), \cdots , f_m (x) \) の各々を割り切るとき、\( h(x) \) は \( f_1 (x), f_2 (x), \cdots ,
f_m (x) \) の公約数であると言います。
また、次数の最も高い公約数を最大公約数と言います。
最大公約数について、次の定理が成り立ちます。
最大公約数について、次の定理が成り立ちます。
\[ \begin{align}
ベズーの等式
\end{align}\]
\( d(x) \) が \( f_1 (x), f_2 (x), \cdots , f_m (x) \) の最大公約数なら、
\[ \begin{align}
f_1 (x) u_1 (x) + f_2 (x) u_2 (x) + \cdots + f_m (x) u_m (x) = d(x) \ \ldots (*)
\end{align}\]
となるような多項式 \( u_1 (x), u_2 (x), \cdots , u_m (x) \) が存在する。
ベズーの等式を証明します。任意の多項式 \( u_1 (x), u_2 (x), \cdots , u_m (x) \) によって \( (*) \) の左辺の形で表せる多項式全体の集合を \( A \)
とします。
\( A \) の元のうち、次数の最低のもの \( \phi (x) \) を取り、
\[ \begin{align}
\phi (x) = \sum _{i=1} ^m f_i (x) u_i (x)
\end{align}\]
とします。次に、\( f_i (x) \) を \( \phi (x) \) で割って、
\[ \begin{align}
f_i (x) = \phi (x) q_i (x) + r_i (x)
\end{align}\]
とします。ただし、\( \rm deg \ \it r_i \rm ( \it x \rm ) \lt deg \ \phi ( \it x \rm ) \) または \( r_i (x) = 0 \) とします。
\[ \begin{align}
r_i (x) &= f_i (x) - \phi (x) q_i (x) \\\\
&= f_i (x) \left\{ 1 - u_i (x) q_i (x) \right\} - \sum _{j \neq i} f_j (x) u_j (x) q_i (x)
\end{align}\]
であるため、\( r_i (x) \in A \) が成り立ちます。
よって、もし \( r_i (x) \neq 0 \) であれば \( \rm deg \ \it r_i \rm ( \it x \rm ) \lt deg \ \phi ( \it x \rm ) \)
が成立つことにより、\( r_i (x) \) は \( \phi (x) \) より次数の低い \( A \) の元となりますが、これは仮定に反します。
ゆえに、\( r_i (x) = 0 \) となります。
従って、\( \phi (x) \) は \( f_1 (x), f_2 (x), \cdots , f_m (x) \) の公約数となります。
よって、\( \rm deg \ \it \phi \rm ( \it x \rm ) \leq deg \ \it d \rm ( \it x \rm ) \) が成り立ちます。
一方、\( \phi (x) \) の式の形から、\( \phi (x) \) は \( d (x) \) で割り切れます。このことと、\( d(x) \) が最大公約数であることより、
\[ \begin{align}
\phi (x) = c d (x) \ \ \left( c \in \mathbb C , \ c \neq 0 \right)
\end{align}\]
となります。ゆえに、
\[ \begin{align}
d (x) &= \frac{1}{c} \phi (x) \\\\
&= \sum _{i=1} ^m f_i (x) \frac{u_i (x)}{c} \ \ \left( c \in \mathbb C , \ c \neq 0 \right)
\end{align}\]
が成り立ちます。
よって、\( u_i (x) / c = v_i (x) \ \left( i = 1, 2, \cdots , m \right) \) と置けば、これは \( (*) \)
を満たす多項式となり、ベズーの等式が成り立ちます。
参考:
[1] 齋藤正彦、線型代数入門、東京大学出版会、1966年3月31日発行
[2] Wikipedia Bézout's identity、https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity#For_polynomials、2025年2月20日閲覧