目次
・チェビシェフの不等式
カヤ
今回は確率変数の期待値からのズレを評価するチェビシェフの不等式を解説しよう。
チェビシェフの不等式
ナユミ
チェビシェフって何だか面白い響きだけど、人の名前よね？
パフヌーティー・チェビシェフは19世紀に活躍したロシアの数学者です。
彼は確率論、統計学および数論の分野で業績を残しました。
彼が指導した数学者も多く、ロシアの数学の父とも呼ばれています。
彼の功績を称えて、月面にはチェビシェフという名前のクレーターがあり、
チェビシェフという名前の小惑星もあります。
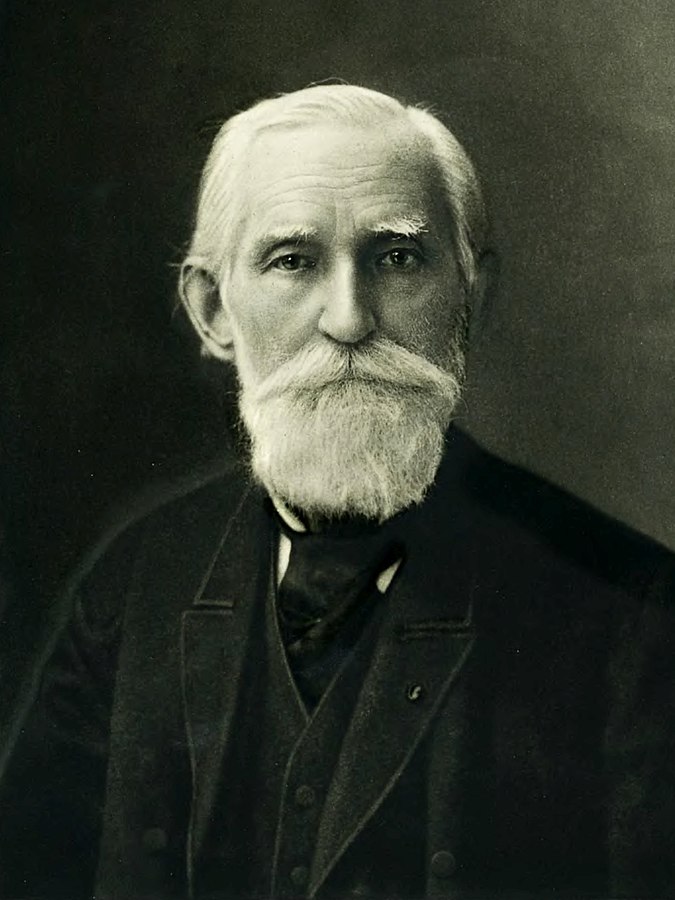
パフヌーティー・チェビシェフ(1821-1894)
ナユミ
すごい数学者なのね。そういえば、確率の公理を導入した人もロシアの数学者じゃなかったっけ？
カヤ
そう、確率の公理を導入したアンドレイ・コルモゴロフもロシアの数学者だ。19世紀から20世紀にかけての確率論の発展に貢献したロシアの著名な数学者には、他にアンドレイ・マルコフとアレクサンドル・リアプノフがいるな。
ナユミ
同じ時代に活躍したロシアの数学者の人が多いのね。それで、チェビシェフの不等式というのはどういうものなのかしら？
カヤ
そうだな、チェビシェフの不等式を説明する前に、この不等式を一般化したものを先に紹介しておこう。
\[ 期待値に関する不等式\]
\( f(x) \) は実区間 \( I \) で定義された非負の単調増加関数とする。\( X \) を確率変数とすると、定数 \( \alpha \in I \ (ただし、f( \alpha ) \neq 0 )\) に対して次の不等式が成り立つ。
\[ P \left( X \geq \alpha \right) \leq \frac{E \left( f(X) \right)}{f( \alpha )}\]
同様に、\( g(x) \) を実区間 \( J \) で定義された非負の単調減少関数とすれば、定数 \( \beta \in J \ (ただし、g( \beta ) \neq 0 )\) に対して次の不等式が成り立つ。
\[ P \left( X \leq \beta \right) \leq \frac{E \left( g(X) \right)}{g( \beta )}\]
カヤ
まずは、確率変数が有限個の値を取る場合に、非負の単調増加関数 \( f(x) \) について成り立つ不等式を証明しよう。
確率変数 \( X \) が、
\[ X = \left\{ X_1 , \ X_2, \cdots ,\ X_n \right\}\]
と表されており、
\[ X_i \leq X_{i+1} \]
\[ i \geq k \ ならば \ X_i \geq \alpha \]
\[ i \lt k \ ならば \ X_i \lt \alpha \]
が成り立つとする。このとき、
\[ \begin{align}
E \left( f(X) \right) &= \sum _{i=1} ^n f(X_i) \cdot P \left( X = X_i \right) \\\\
& \geq \sum _{i=k} ^n f(X_i) \cdot P \left( X = X_i \right) \\\\
& \geq f( \alpha ) \sum _{i=k} ^n P \left( X = X_i \right) \\\\
&= f( \alpha ) \cdot P \left( X \geq \alpha \right) \\\\
P \left( X \geq \alpha \right) & \leq \frac{E \left( f(X) \right)}{f( \alpha )}
\end{align}\]
ナユミ
次は単調減少関数のときね。
確率変数 \( X \) が、
\[ X = \left\{ X_1 , \ X_2, \cdots ,\ X_n \right\}\]
と表されており、
\[ X_i \leq X_{i+1} \]
\[ i \gt k \ ならば \ X_i \gt \beta \]
\[ i \leq k \ ならば \ X_i \leq \beta \]
が成り立つとする。このとき、
\[ \begin{align}
E \left( g(X) \right) &= \sum _{i=1} ^n g(X_i) \cdot P \left( X = X_i \right) \\\\
& \geq \sum _{i=1} ^k g(X_i) \cdot P \left( X = X_i \right) \\\\
& \geq g( \beta ) \sum _{i=1} ^k P \left( X = X_i \right) \\\\
&= g( \beta ) \cdot P \left( X \leq \beta \right) \\\\
P \left( X \leq \beta \right) & \leq \frac{E \left( g(X) \right)}{g( \beta )}
\end{align}\]
カヤ
次は、これらを確率変数 \( X \) が連続な値をとるときに証明してみよう。
確率変数 \( X \) が、\( - \infty \leq a \leq X \leq b \leq \infty \) を満たす実数値をとるとする。
また、\( X \) の確率密度関数を \( h(x) \) とすると、
\[ \begin{align}
E \left( f(X) \right) &= \int _a ^b f(x)h(x) dx \\\\
& \geq \int _{\alpha} ^b f(x)h(x) dx \\\\
& \geq f( \alpha ) \int _{\alpha} ^b h(x) dx \\\\
&= f( \alpha ) \cdot P \left( X \geq \alpha \right) \\\\
P \left( X \geq \alpha \right) & \leq \frac{E \left( f(X) \right)}{f( \alpha )}
\end{align}\]
ナユミ
\( \sum \) が \( \int \) に変わっただけね。\( a \) と \( \alpha \) が小さいと紛らわしいわね…
カヤ
見間違えないようにしてくれよな。次は、単調減少の方。
確率変数 \( X \) が、\( - \infty \leq a \leq X \leq b \leq \infty \) を満たす実数値をとるとする。
また、\( X \) の確率密度関数を \( h(x) \) とすると、
\[ \begin{align}
E \left( g(X) \right) &= \int _a ^b g(x)h(x) dx \\\\
& \geq \int _{a} ^{\beta} g(x)h(x) dx \\\\
& \geq g( \beta ) \int _{a} ^{\beta} h(x) dx \\\\
&= g( \beta ) \cdot P \left( X \leq \beta \right) \\\\
P \left( X \leq \beta \right) & \leq \frac{E \left( g(X) \right)}{g( \beta )}
\end{align}\]
ナユミ
これも一緒ね。
カヤ
そうだな。じゃあ、これらの不等式を使って、次のチェビシェフの不等式を証明しよう。
\[ チェビシェフの不等式\]
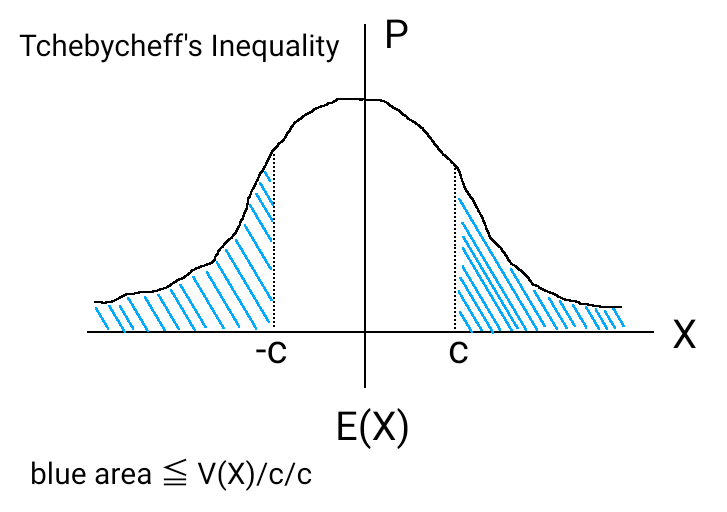
定数 \( c \gt 0 \) に対して、次の不等式が成り立つ。
\[ P \left( |X - E(X)| \geq c \right) \leq \frac{E \left( \left( X - E(X) \right) ^2 \right)}{c^2} = \frac{V(X)}{c^2} \]
この不等式の意味は「確率変数と期待値との差の絶対値が \( c \) 以上になる確率は、分散を \( c^2 \) で割ったもの以下である」ということです。
例えば、この不等式の定数に \( c = qE(X) \) と代入すれば、確率変数と期待値との差の絶対値が期待値の \( q \) 倍以上になる確率の上限値を評価することができます。
ナユミ
この不等式の証明はどうするのかしら？
カヤ
さっきの不等式が使えるように変形すればいいな。まずは確率変数 \( X \) が有限個の値を取る場合から。
確率変数 \( X \) が、
\[ X = \left\{ X_1 , \ X_2, \cdots ,\ X_n \right\}\]
と表されており、
\[ X_i \leq X_{i+1} \]
\[ i \leq k \ \ ならば \ \ X_i - E(X) \leq -c \]
\[ k \lt i \lt l \ \ ならば \ \ -c \lt X_i - E(X) \lt c \]
\[ i \geq l \ \ ならば \ \ X_i - E(X) \geq c \]
が成り立つとする。このとき、
\[ \begin{align}
E \left( \left( X - E(X) \right) ^2 \right) &= \sum _{i=1} ^n \left( x_i - E(X) \right) ^2 \cdot P \left( X = X_i \right) \\\\
& \geq \sum _{i=1} ^{k} \left( x_i - E(X) \right) ^2 \cdot P \left( X = X_i \right) \\\\
& \ \ \ \ + \sum _{i=l} ^{n} \left( x_i - E(X) \right) ^2 \cdot P \left( X = X_i \right) \\\\
& \geq c^2 \left\{ \sum _{i=1} ^{k} P \left( X = X_i \right) + \sum _{i=l} ^{n} P \left( X = X_i \right) \right\} \\\\
&= c^2 P \left( |X - E(X)| \geq c \right) \\\\
P \left( |X - E(X)| \geq c \right) & \leq \frac{E \left( \left( X - E(X) \right) ^2 \right)}{c^2} = \frac{V(X)}{c^2}
\end{align}\]
ナユミ
うーんと、条件設定のところがごちゃごちゃしてるけど、要は \( k \lt i \lt l \) の部分をくり抜こうとしてるのね。
カヤ
そういうこと。\( \left( x_i - E(X) \right) ^2 \) は2乗の中身が負のところでは単調減少、正のところでは単調増加だから、それぞれの部分でさっきの不等式を使ったんだ。
ナユミ
確率変数が連続の場合も同じように証明できそうね。
カヤ
ああ。連続の場合はこうなる。
確率変数 \( X \) が、\( - \infty \leq a \leq X \leq b \leq \infty \) を満たす実数値をとるとする。
また、\( X \) の確率密度関数を \( h(x) \) とすると、
\[ \begin{align}
E \left( \left( X - E(X) \right) ^2 \right) &= \int _{a} ^b \left( x - E(X) \right) ^2 h(x) dx \\\\
& \geq \int _{a} ^{-c + E(X)} \left( x - E(X) \right) ^2 h(x) dx \\\\
& \ \ \ \ + \int _{c + E(X)} ^{b} \left( x - E(X) \right) ^2 h(x) dx \\\\
& \geq c^2 \left\{ \int _{a} ^{-c + E(X)} h(x) dx + \int _{c + E(X)} ^{b} h(x) dx \right\} \\\\
&= c^2 P \left( |X - E(X)| \geq c \right) \\\\
P \left( |X - E(X)| \geq c \right) & \leq \frac{E \left( \left( X - E(X) \right) ^2 \right)}{c^2} = \frac{V(X)}{c^2}
\end{align}\]
ナユミ
ふむふむ、\( |X - E(X)| \geq c \) は \( -c \leq X - E(X) \leq c \) 、つまり、
\[ -c + E(X) \leq X \leq c + E(X) \]
のことだから、この条件で積分区間を分けているのね。
カヤ
そういうことだな。じゃあ、今回はここまでにしよう。
参考：
[1] Wikipedia Pafnuty Chebyshev、https://en.wikipedia.org/wiki/Pafnuty_Chebyshev、2023年10月6日閲覧
[2] A.N.Kolmogorov 著、Nathan Morrison 英訳、FOUNDATIONS OF THE THEORY OF PROBABILITY、CHELSEA PUBLISHING COMPANY NEW YORK、1950年
前の記事
第18話
確率分布・確率密度
・期待値・分散
確率分布・確率密度
・期待値・分散
次の記事
第20話
大数の弱法則
大数の弱法則