ある日、ある電気屋にて…

ナユミ
玄関の電球と、ついでに切らしてた乾電池、と。よし、要るものは買ったわね。カヤちゃんは…、あ、居た。

カヤ
うーん、家のテレビも壊れたら次は4Kにするかなあ。

ナユミ
買い物終わったよ!カヤちゃんテレビ見てるの?最近のテレビは高画質で綺麗だよね。

カヤ
そうだなあ。まあでもゲームでもしない限りそこまで気にならないけどな。

ナユミ
そう?私は小3ぐらいのときに家のテレビがブラウン管から液晶に変わって感動したんだけどな。

カヤ
カヤは家のテレビはずっと液晶だったからな。ブラウン管テレビは社会の資料集で初めて見たな。

ナユミ
この現代っ子め…。まあでも、今じゃあ液晶テレビは当たり前よね。有機ELとかも広まってるし、ブラウン管じゃない薄型のテレビっていつ頃から広まってたんだろ?

カヤ
じゃあ、家に帰ってから薄型テレビの歴史を振り返りながら、技術の普及のモデルの話でもするかな。
薄型テレビの歴史

ナユミ
液晶テレビっていつ頃から出始めたのかしら?
液晶テレビは画面の小さなポケットサイズのものであれば、1984年には登場していました。
リビングに置いて見るようなサイズのものは1995年に発売されましたが、
実際に一般家庭に普及し始めたのは2001年頃からです。
このころシャープからAQUOSが発売されています。
同じ時期に、液晶テレビと並んでプラズマテレビも一般家庭に普及し始めました。
プラズマテレビはスポーツなどの動きが激しい映像でも見やすく、画面のコントラストが高く立体的な映像を見ることができるという特徴があります。
また、2000年代前半は画面サイズが大きな液晶テレビが技術的に生産可能ではなかったため、大きな画面サイズも用意できるプラズマテレビは高級モデルとして人気がありました。
ところが、2010年前後あたりで液晶テレビの大型化が進み、プラズマテレビの売りであった大画面という魅力に陰りが出始めます。
液晶テレビの価格もプラズマテレビと同程度にまで下がり、さらにプラズマテレビの欠点である電力消費の激しさと重量が大きいという点を液晶テレビはクリアしていたため、プラズマテレビの売りが見当たらなくなってしまいます。
結局、プラズマテレビは2014年3月を最後に店頭から消えることになりました。
現在、店頭に並んでいるのは液晶テレビと有機ELになります。
有機ELディスプレイのテレビは2007年に始めて発売されました。
有機ELは価格が高いものの、画質はプラズマテレビや液晶テレビより優れており、プラズマテレビほどの電力消費は無く、重量に関しては液晶テレビよりも軽くすることができます。
また、視野角がほぼ180°あるという点も魅力であり、大型の高級モデルとして液晶テレビと共存し続けています。
続いて、日本の二人以上の世帯についての液晶・プラズマ・有機EL、3種からなる薄型テレビの普及率を見てみます。
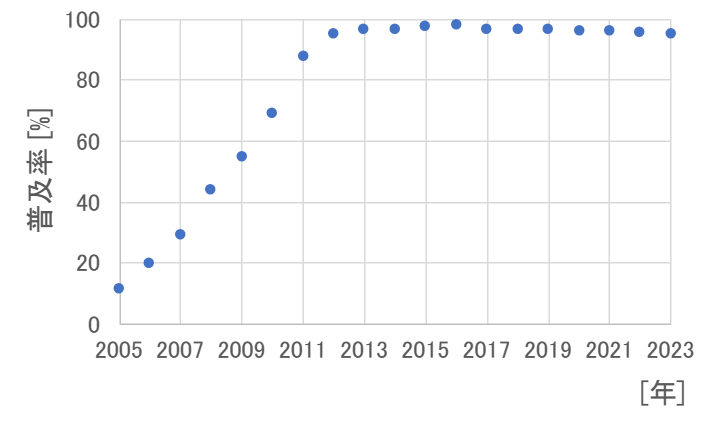
「消費動向調査 長期時系列表 1-3 二人以上の世帯(主要耐久消費財等) 主要耐久消費財の普及率の推移 カラーテレビ_薄型(液晶、プラズマ等)」より作成
2005年以降、薄型テレビの普及は二人以上の世帯で年に約10%強の増加率で進み、8年後の2013年には普及率はほぼ100%になっています。

カヤ
ここからは、この普及率の変化を微分方程式で表現することを考えてみよう。

ナユミ
今からモデル化が始まるのね…。
技術の普及

カヤ
今回は、人から聞くうわさ話と広告、これらを考慮して技術や製品が広まっていく過程をモデル化してみよう。
最終的に普及「率」を求めたいので、「製品を買ったグループ」と「製品をまだ買っていないグループ」の二つがまずは必要となります。
また、状況を単純化して、「製品を買ったグループ」と「製品をまだ買っていないグループ」の合計は変わらないとします。
これは、今の例だと、日本の二人以上の世帯数がモデル化を考えている期間で一定であると仮定することになります。
実際、次のグラフの通り、薄型テレビが普及し始めた2001年以降、二人以上の世帯数にそれほど大きな変動はありません。
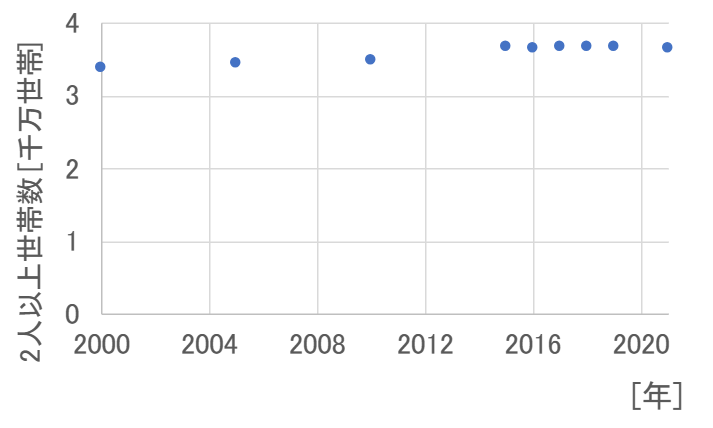
2000年、2005年、2010年のデータは「平成27年国勢調査 世帯構造等基本集計結果 結果の概要 表Ⅰ-1 総世帯数,一般世帯数及び施設等の世帯数の推移-全国(平成 12 年~27 年)」より作成。
2015年以降のデータは「厚生労働省HP 統計情報・白書 > 各種統計調査結果 > 統計要覧 > 厚生統計要覧(令和4年度) > 第1編 人口・世帯 第3章 世帯 第1-46表 世帯数・構成割合,世帯構造×年次別」より作成。
実際には、この世帯数の中でも新しい世帯と無くなった世帯が入れ替わっていますが、今回は単純化のため考える期間では世帯数は一定で世帯の入れ替わりも無いと仮定します。
このように仮定すると、「製品を買ったグループ」と「製品をまだ買っていないグループ」を次のように表すことができます。
\( N \) :すべてのグループ
\( x \) :製品を買ったグループ
\( N - x \) :製品をまだ買っていないグループ
次に、うわさ話の効果を表現するため、「製品を買った人の製品についての評価は買ってないすべての人に伝わる」という仮定をします。
この仮定からさらに、うわさ話の効果は「製品を買った人と買ってない人のペアの数」に比例すると仮定します。
すると、ペアの数は「製品を買った人数」と「製品を買ってない人の人数」のかけ算で表せるので、次の式を考えることができます。
短い時間区間 \( \Delta t \) の間の製品を買ったグループの増加数 \( \Delta x \) は、「製品を買った人と買ってない人のペアの数」に比例する。すなわち、
\[ \Delta x = ax \left( N - x \right) \Delta t \]
ここで、\( a \) は製品を買った人の製品に対する評価を表す定数である。
一方、広告の方は単純に、製品を買ってない人は全員、製品の広告を見ていると仮定して、次の数式を立てます。
短い時間区間 \( \Delta t \) の間の製品を買ったグループの増加数 \( \Delta x \) は、「製品を買ってない人の数」に比例する。すなわち、
\[ \Delta x = b \left( N - x \right) \Delta t \]
ここで、\( b \) は広告の効果を表す定数である。
これでうわさ話と広告、どちらも数式で表せたので両方の効果を足し算して一つにまとめます。
短い時間区間 \( \Delta t \) の間の製品を買ったグループの増加数 \( \Delta x \) は次式で表される。
\[ \Delta x = ax \left( N - x \right) \Delta t + b \left( N - x \right) \Delta t \]
ここで、\( a \) は製品を買った人の製品に対する評価を表す定数、\( b \) は広告の効果を表す定数である。
続いて、この式を微分方程式の形に直していきます。
\[ \begin{align}
\Delta x &= ax \left( N - x \right) \Delta t + b \left( N - x \right) \Delta t \\\\
\frac{\Delta x}{\Delta t} &= ax \left( N - x \right) + b \left( N - x \right)
\end{align} \]
ここで、\( x = x(t) \) とし、
\[ \Delta x = x(t + h) - x(t) \]
\[ \Delta t = (t + h) - t = h \]
とすれば、
\[ \begin{align}
\frac{\Delta x}{\Delta t} &= ax \left( N - x \right) + b \left( N - x \right) \\\\
\frac{x(t + h) - x(t)}{h} &= ax \left( N - x \right) + b \left( N - x \right)
\end{align} \]
\( h \to 0 \) の極限をとると、
\[ \begin{align}
\lim _{h \to 0} \frac{x(t + h) - x(t)}{h} &= \lim _{h \to 0} \left\{ ax \left( N - x \right) + b \left( N - x \right) \right\} \\\\
\frac{dx}{dt} &= ax \left( N - x \right) + b \left( N - x \right) \\\\
\frac{dx}{dt} &= \left(ax + b \right) \left( N - x \right)
\end{align} \]
この微分方程式は変数分離法で解くことができます。
\[ \begin{align}
\frac{dx}{dt} &= \left(ax + b \right) \left( N - x \right) \\\\
\frac{1}{\left(ax + b \right) \left( N - x \right)} \frac{dx}{dt} &= 1 \\\\
\int \frac{1}{\left(ax + b \right) \left( N - x \right)} \frac{dx}{dt} dt &= \int 1 dt \\\\
\int \frac{1}{\left(ax + b \right) \left( N - x \right)} dx &= \int 1 dt \\\\
\int \frac{1}{aN+b} \left( \frac{a}{ax+b} + \frac{1}{N-x} \right) dx &= \int 1 dt \\\\
\int \left( \frac{a}{ax+b} + \frac{1}{N-x} \right) dx &= \left( aN + b \right) \int 1 dt \\\\
\int \frac{a}{ax+b} dx + \int \frac{1}{N-x} dx &= \left( aN + b \right) \int 1 dt \\\\
\ln \left( ax+b \right) - \ln \left( N-x \right) &= \left( aN + b \right) t + C \\\\
\ln \frac{ax+b}{N-x} &= \left( aN + b \right) t + C \\\\
\end{align} \]
初期値は \( t = 0 \) において \( x = x_0 \) とすると、積分定数は
\[ C = \ln \frac{ax_0+b}{N-x_0}\]
と求まります。これを先ほどの式に代入します。
\[ \begin{align}
\ln \frac{ax+b}{N-x} &= \left( aN + b \right) t + \ln \frac{ax_0+b}{N-x_0} \\\\
\ln \frac{ax+b}{N-x} &= \ln e^{\left( aN + b \right) t} + \ln \frac{ax_0+b}{N-x_0} \\\\
\ln \frac{ax+b}{N-x} &= \ln \left\{ e^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0} \right\} \\\\
\frac{ax+b}{N-x} &= e^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0} \\\\
ax+b &= \left( N-x \right) \cdot e^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0} \\\\
x \left\{ a + e^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0} \right\} &= Ne^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0} - b \\\\
x &= \frac{Ne^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0} - b}{a + e^{\left( aN + b \right) t} \cdot \frac{ax_0+b}{N-x_0}} \\\\
x &= \frac{\left( ax_0+b \right) N e^{\left( aN + b \right) t} - b \left( N-x_0 \right)}{a \left( N-x_0 \right) + \left( ax_0+b \right) e^{\left( aN + b \right) t}}
\end{align} \]
最後の式が製品を買ったグループを表しています。
実際に普及率 [%] を計算する際は最後の式をすべてのグループ \( N \) で割って100をかけます。
先ほどの薄型テレビの普及率のデータにモデルを合わせてみます。
まずは1世帯が薄型テレビを購入したと仮定して、\( x_0 = 1 \) とします。
すべてのグループにあたるのは今回の場合二人以上の世帯数なので、3.5千万世帯、つまり \( N = 3.5 \times 10^7 \) とします。
また、薄型テレビが日本に普及し始めたのは2001年頃なので、2001年を時刻 \( t = 0 \) にあたる年とします。
この条件で、\( a = 1.7 \times 10^{-8} \) 、\( b = 0.008 \) としてモデルと実測値を比較したのが次のグラフになります。
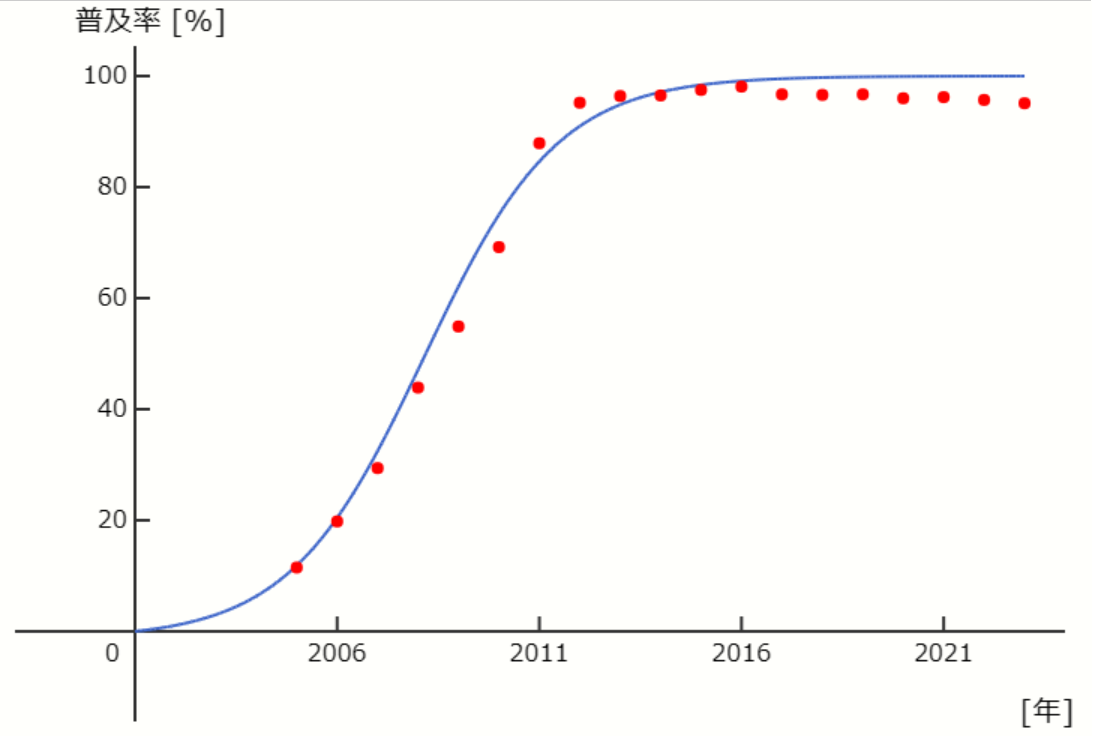

ナユミ
実際のデータをうまく再現できているわね。

カヤ
そうだな。これと合わせて、うわさ話と広告が普及率の増加速度にそれぞれ与える影響の大きさを見てみよう。
次のグラフは、モデルの微分方程式
\[ \frac{dx}{dt} = ax \left( N - x \right) + b \left( N - x \right) \]
の右辺第1項をうわさ話の効果、第2項を広告の効果として、先ほどの薄型テレビの普及率を再現したモデルのパラメータと同じ値をつかってグラフを書いたものです。
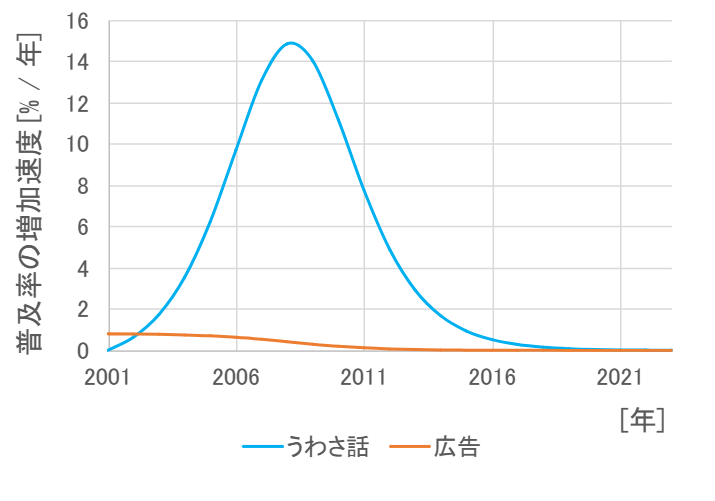
始めの1年くらいは広告の影響が大きいですが、その後はほとんどうわさ話の影響で普及率は増えていることがわかります。
新商品を売るときは認知度の低い売り始めにこそ、継続的な広告を行う必要があるということだと思います。

ナユミ
人のうわさって恐ろしいわね。

カヤ
いいね!や高評価を気にする人が多いのも、こういうところに理由があるのかもな。

ナユミ
うわさに振り回されすぎないように気を付けないとね。

カヤ
そうだな。
参考:
[1] David Burghes/Morag Borrie 著、 垣田高夫/大町久佐栄 訳、微分方程式で数学モデルを作ろう、日本評論社、1990年4月28日発行
[2] 消費動向調査 長期時系列表 1-3 二人以上の世帯(主要耐久消費財等) 主要耐久消費財の普及率の推移、https://www.e-stat.go.jp/stat-search/file-download?statInfId=000040046130&fileKind=0、2023年8月22日閲覧
[3] 厚生労働省HP 統計情報・白書 > 各種統計調査結果 > 統計要覧 > 厚生統計要覧(令和4年度) > 第1編 人口・世帯 第3章 世帯 第1-46表 世帯数・構成割合,世帯構造×年次別、https://www.mhlw.go.jp/toukei/youran/datar04k/1-46.xlsx、2023年8月22日閲覧
[4] プラズマテレビはなぜ衰退したか--旗振り役パナソニック会長退任へ、https://japan.cnet.com/article/35030396/、2023年8月23日閲覧
[5] プラズマテレビの魅力とは?なぜ希少価値があるのか?、https://dorekau.com/58006、2023年8月23日閲覧
[6] 【特別企画】パナソニック プラズマ事業終息に寄せて、https://av.watch.impress.co.jp/docs/topic/621839.html、2023年8月23日閲覧
[7] 液晶テレビはどのように発展してきたのか?液晶の歴史でおさえておきたいポイント7選、https://pentabu.it-kaden.com/液晶テレビはどのように発展してきたのか?液晶/、2023年8月23日閲覧
[8] Wikipedia 有機エレクトロルミネッセンス、https://ja.wikipedia.org/wiki/有機エレクトロルミネッセンス、2023年8月23日閲覧
[9] 有機ELテレビとは?液晶テレビと何が違うの?有機ELテレビの特徴やメリット、選び方や注意点も解説します!、https://www.japanet.co.jp/shopping/lcd-tv/lcd-tv_ole.html、2023年8月23日閲覧
[10] テレビの電気代を節約する方法5選!プラズマテレビは買い替えた方がいい?、https://www.setsuyakujutsu.com/entry/tv-setuyakujutu、2023年8月23日閲覧
[11] 平成27年国勢調査 世帯構造等基本集計結果 結果の概要、https://www.stat.go.jp/data/kokusei/2015/kekka/kihon3/pdf/gaiyou.pdf、2023年8月23日閲覧
前の記事
第5話
ロジスティック曲線
次の記事

第7話
フェルメールの贋作
~メーヘレンの事件~