
ナユミ
カヤちゃん、マルサスモデルについてちょっと聞きたいことがあるんだけど?

カヤ
なんだ?

ナユミ
マルサスモデルって人口がどこまでも増加していくじゃない。あれって、どこかで頭打ちになるようなモデルはないのかなあと思って。

カヤ
そういうモデルはいくつかあるが、一番有名なのはロジスティック曲線かな。
ロジスティック曲線
ロジスティック曲線は1837年にオランダの数理生物学者ヴェアフルストが発表しました。
彼はマルサスモデルが人口の際限のない増加を予測することに対する修正として、ロジスティック曲線を解とする微分方程式を提案しました。

ピエール=フランソワ・ヴェアフルスト
彼の提案した微分方程式は、人口の増加速度は人口に比例して増加すると同時に、人口の2乗に比例して減少するというものでした。ヴェアフルストが発表したものを少し整理したものが次の式です。
\[ \frac{dN}{dt} = rN \left( 1 - \frac{N}{N_{\infty}} \right) \]
\( N \) :人口、\( t \) :時刻、\( r \) :比例定数、\( N_{\infty} \) :環境収容力
環境収容力 \( N_{\infty} \) は人口の上限を与える定数です。
これは、上の微分方程式の右辺に \( N = N_{\infty} \) を代入すると \( \frac{dN}{dt} = 0 \) となることからもわかります。
この微分方程式はマルサスモデルと同じく変数分離法を使えば解くことができます。
\[ \begin{align}
\frac{dN}{dt} &= rN \left( 1 - \frac{N}{N_{\infty}} \right) \\\\
\frac{1}{N \left( 1 - \frac{N}{N_{\infty}} \right)} \cdot \frac{dN}{dt} &= r \\\\
\left\{ \frac{1}{N} + \frac{\frac{1}{N_{\infty}}}{1 - \frac{N}{N_{\infty}}} \right\} \cdot \frac{dN}{dt} &= r \\\\
\int \left\{ \frac{1}{N} + \frac{\frac{1}{N_{\infty}}}{1 - \frac{N}{N_{\infty}}} \right\} \cdot \frac{dN}{dt} dt &= \int r dt \\\\
\int \left\{ \frac{1}{N} + \frac{\frac{1}{N_{\infty}}}{1 - \frac{N}{N_{\infty}}} \right\} dN &= rt + C \\\\
\int \frac{1}{N} dN + \int \frac{\frac{1}{N_{\infty}}}{1 - \frac{N}{N_{\infty}}} dN &= rt + C \\\\
\ln N - \ln \left( 1 - \frac{N}{N_{\infty}} \right) &= rt + C \\\\
\ln \frac{N}{1 - \frac{N}{N_{\infty}}} &= rt + C \\\\
\end{align}\]
続いて、初期値を導入して積分定数 \( C \) を定め、特解を求めます。
\( t = 0 \) で \( N = N_0 \) とする。このとき、
\[ \begin{align}
\ln \frac{N}{1 - \frac{N}{N_{\infty}}} &= rt + C \\\\
\ln \frac{N_0}{1 - \frac{N_0}{N_{\infty}}} &= C \\
\end{align}\]
よって、
\[ \begin{align}
\ln \frac{N}{1 - \frac{N}{N_{\infty}}} &= rt + \ln \frac{N_0}{1 - \frac{N_0}{N_{\infty}}} \\\\
\ln \frac{N}{1 - \frac{N}{N_{\infty}}} &= \ln e^{rt} + \ln \frac{N_0}{1 - \frac{N_0}{N_{\infty}}} \\\\
\ln \frac{N}{1 - \frac{N}{N_{\infty}}} &= \ln \frac{N_0 e^{rt}}{1 - \frac{N_0}{N_{\infty}}} \\\\
\frac{N}{1 - \frac{N}{N_{\infty}}} &= \frac{N_0 e^{rt}}{1 - \frac{N_0}{N_{\infty}}} \\\\
\frac{N}{N_{\infty} - N} &= \frac{N_0 e^{rt}}{N_{\infty} - N_0} \\\\
\frac{N_{\infty} - N}{N} &= e^{-rt} \left( \frac{N_{\infty} - N_0}{N_0} \right) \\\\
\frac{N_{\infty}}{N} - 1 &= e^{-rt} \left( \frac{N_{\infty}}{N_0} - 1 \right) \\\\
\frac{N_{\infty}}{N} &= e^{-rt} \left( \frac{N_{\infty}}{N_0} - 1 \right) + 1 \\\\
\frac{N}{N_{\infty}} &= \frac{1}{\left\{ e^{-rt} \left( \frac{N_{\infty}}{N_0} - 1 \right) + 1 \right\}} \\\\
N &= \frac{N_{\infty}}{\left\{ e^{-rt} \left( \frac{N_{\infty}}{N_0} - 1 \right) + 1 \right\}} \\\\
\end{align}\]

ナユミ
長かったわね、最後の式がロジスティック曲線?

カヤ
そういうことだな。
\( N_0 = 1 \) 、\( N_{\infty} = 100 \) として、\( r \) の値を0.1、0.3、0.5でロジスティック曲線を比較したのが次のグラフです。
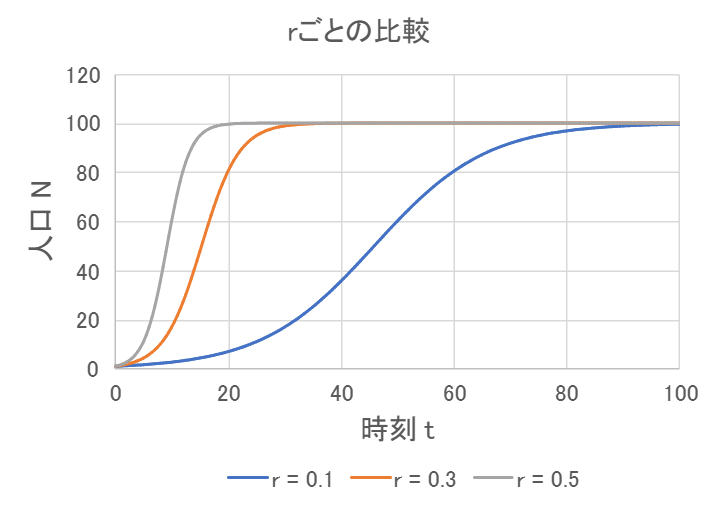
\( r \) の値が大きいほど、速く \( N \) が \( N_{\infty} \) に近づいています。
次に、\( N_0 = 1 \) 、\( r = 0.1 \) として、\( N_{\infty} \) の値を100、200、300でロジスティック曲線を比較しました。
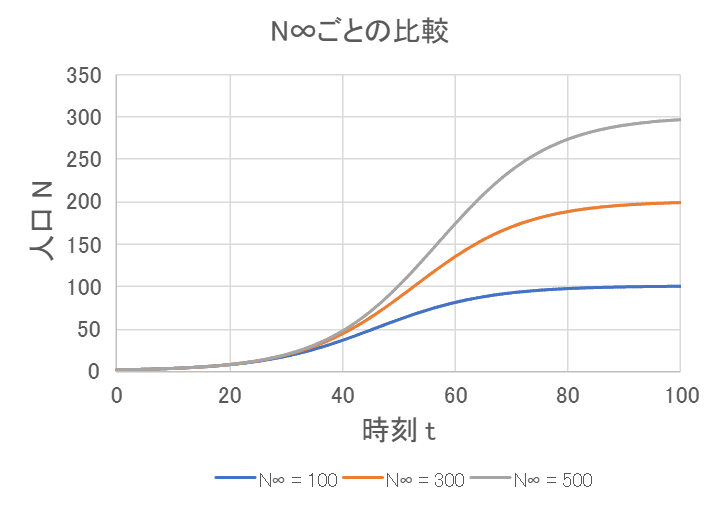
\( t = 30 \) くらいまでは3つの曲線にあまり差はありませんが、それより後はそれぞれの \( N_{\infty} \) に向けて増加していきます。
ガウゼの実験

ナユミ
ロジスティック曲線を実際のデータにあてはめた例はあるの?

カヤ
いろいろあるが、一つ有名なものとしてソ連・ロシアの生物学者ゲオルギー・ガウゼによる酵母の培養実験(1932)があるな。
ガウゼの実験では2種類の酵母を培養してその体積を測定しています。ここではその内の一つである \( Saccharomyces \ cerevisiae \) のデータとそれに対するロジスティック曲線の当てはめを紹介します。
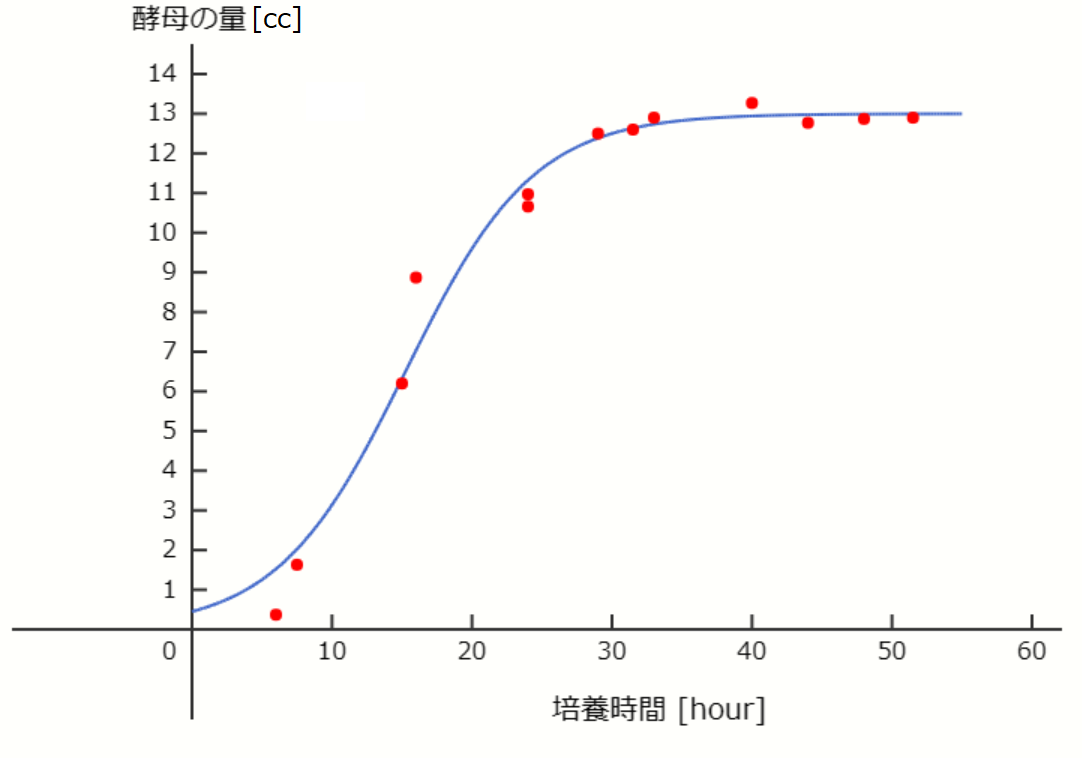
参考[3]のTableⅠより作成。赤丸が酵母の量の実測値、青線がロジスティック曲線。

ナユミ
ロジスティック曲線の上に実測値が綺麗に乗ってるわね。

カヤ
そうだよな。ロジスティック曲線は酵母の他にも、ゾウリムシやキイロショウジョウバエの増殖にもうまく適用できることが知られているぞ。

ナユミ
人口の予測には使えないの?

カヤ
元々は人口の予測のために生まれたモデルだが、残念ながら現在ではほとんど使われてないみたいだな。

ナユミ
やっぱり人口の予測は難しいのね。

カヤ
そうだな。生物の種類によって個体数の増加の様子は様々だからな。その都度適切なモデルを探っていく必要はあるだろうな。
参考:
[1] David Burghes/Morag Borrie 著、 垣田高夫/大町久佐栄 訳、微分方程式で数学モデルを作ろう、日本評論社、1990年4月28日発行
[2] Wikipedia ロジスティック方程式、https://ja.wikipedia.org/wiki/ロジスティック方程式、2023年8月21日閲覧
[3] G.F.GAUSE, EXPERIMENTAL STUDIES ON THE STRUGGLE FOR EXISTENCE Ⅰ. MIXED POPULATION OF TWO SPECIES OF YEAST, Journal of Experimental Biology, Volume 9, Issue 4, 1932
前の記事

第4話
カビの増殖
次の記事

第6話
技術の普及
~薄型テレビの普及率~






