第51話  複素関数の微分

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 6話、 22話、 26話、 47話、 50話

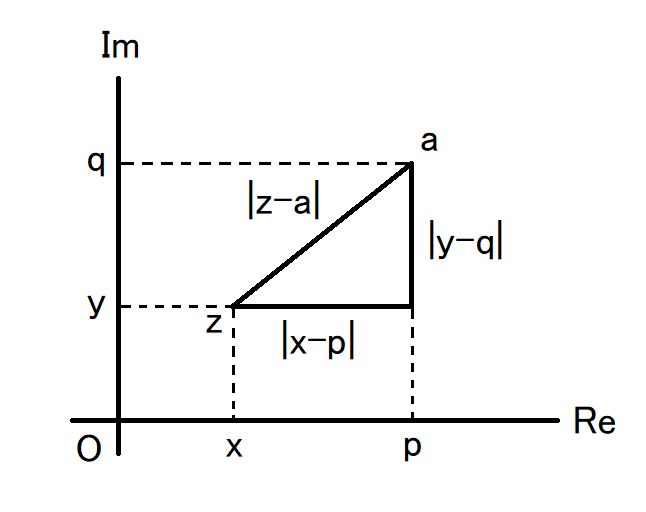
　上の定義における \( z \to a \) は、\( z = x + iy \) 、\( a = p + iq \) とするなら、\( \left( x,y \right) \to \left( p, q \right) \) と書き換えることができます。 これは、下図に示した複素平面内の直角三角形の辺の長さの大小関係を考えると、 \[ \begin{align} 0 \leq \left| x - p \right| \leq \left| z - a \right| \leq \left| x - p \right| + \left| y - q \right| \\\\ 0 \leq \left| y - q \right| \leq \left| z - a \right| \leq \left| x - p \right| + \left| y - q \right| \end{align}\] が成り立つことから、\( z \to a \) は \( \left( x,y \right) \to \left( p, q \right) \) と同値であることによります。

　同様に、\( f \left( z \right) \to b \) は、\( f \left( z \right) = u \left( x,y \right) + i v \left( x,y \right) \) 、\( b = s + i t \) と表されているとき、 \( \left( u \left( x,y \right), v \left( x,y \right) \right) \to \left( s,t \right) \) と書き換えることができます。

　導関数についても、実数変数関数の微分と同様の表記を用いて、次で定義します。

　\( f \left( z \right) \) が領域 \( D \) の各点で複素微分可能であり、かつ、導関数 \( f ' \left( z \right) \) が \( D \) で連続であるとき、\( f \left( z \right) \) は \( D \) で正則であると言います。

　また、微分可能と連続性についても、実数変数関数の場合と同じく、次が成り立ちます。

証明： \[ \begin{align} \lim _{z \to a} \left\{ f \left( z \right) - f \left( a \right) \right\} &= \lim _{z \to a} \frac{f \left( z \right) - f \left( a \right)}{z-a} \cdot \left( z-a \right) \\\\ &= f'(z) \cdot 0 = 0 \end{align}\]

　実数変数一変数関数の微分において成り立っていた「定数倍と和、差の微分公式」、「積と商の微分公式」、「合成関数の微分公式」は、いずれも複素微分においても同様の公式が成り立ちます。 証明は実数変数のものと同様なので、ここでは公式だけ示しておきます。

証明： \( f \left( z \right) \) が \( D \) で正則とする。 \( z = x + iy \) を \( D \) の一点とする。 また、\( z + h \in D \) を満たす、絶対値が十分小さい実数 \( h \) を取る。次の式、 \[ \begin{align} \frac{f \left( z + h \right) - f \left( z \right)}{h} = \frac{u \left( x+h, y \right) - u \left( x, y \right)}{h} + i \frac{v \left( x+h, y \right) - v \left( x, y \right)}{h} \end{align}\] において、\( h \to 0 \) とすると、左辺は \( f ' \left( z \right) \) に収束する。 よって、右辺の極限値も存在し、それは \( f ' \left( z \right) \) に等しい。従って、 \[ \begin{align} f ' \left( z \right) = \frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x} \ \ldots (1) \end{align}\] 同様に、\( z + ik \in D \) を満たす、絶対値が十分小さい実数 \( k \) を取る。次の式、 \[ \begin{align} \frac{f \left( z + ik \right) - f \left( z \right)}{ik} = \frac{1}{i} \left\{ \frac{u \left( x, y+k \right) - u \left( x, y \right)}{k} + i \frac{v \left( x, y+k \right) - v \left( x, y \right)}{k} \right\} \end{align}\] において、\( k \to 0 \) とすると、左辺は \( f ' \left( z \right) \) に収束する。 よって、右辺の極限値も存在し、それは \( f ' \left( z \right) \) に等しい。従って、 \[ \begin{align} f ' \left( z \right) &= \frac{1}{i} \left( \frac{\partial u}{\partial y} + i \frac{\partial v}{\partial y} \right) \\\\ &= \frac{\partial v}{\partial y} - i \frac{\partial u}{\partial y} \ \ldots (2) \end{align}\] \( (1) \) 、\( (2) \) と \( f ' \left( z \right) \) が \( D \) で連続であるという条件を合わせると、 \[ \begin{align} \frac{\partial u}{\partial x}, \ \frac{\partial u}{\partial y}, \ \frac{\partial v}{\partial x}, \ \frac{\partial v}{\partial y} \end{align}\] も \( D \) で連続となり、\( u \left( x, y \right) \) 、\( v \left( x, y \right) \) はともに \( D \) を定義域とする \( C^1 \) - 関数となる。 また、\( (1) \) 、\( (2) \) の実部と虚部をそれぞれ見比べることで、Cauchy-Riemann の関係式を得る。

　逆に、\( u \left( x, y \right) \) 、\( v \left( x, y \right) \) がともに \( D \) を定義域とする \( C^1 \) - 関数であり、Cauchy-Riemann の関係式が \( D \) の各点で成立すると仮定する。 \( z = x + iy \) を \( D \) の一点とする。 また、\( z + h + ik \in D \) を満たす、絶対値が十分小さい実数 \( h \) 、\( k \) を取り、 \[ \begin{align} \zeta = z + h + ik \end{align}\] とおく。2 変数平均値の定理および Cauchy-Riemann の関係式より、次式を満たす \( \theta _1 \) 、\( \theta _2 \)（ \( 0 \lt \theta _1 , \theta _2 \lt 1 \) ）が存在する。 \[ \begin{align} u \left( x+h, y+k \right) - u \left( x, y \right) &= h \frac{\partial u}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) + k \frac{\partial u}{\partial y} \left( x + \theta _1 h , y + \theta _1 k \right) \\\\ &= h \frac{\partial u}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) - k \frac{\partial v}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) \\\\ v \left( x+h, y+k \right) - v \left( x, y \right) &= h \frac{\partial v}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) + k \frac{\partial v}{\partial y} \left( x + \theta _2 h , y + \theta _2 k \right) \\\\ &= h \frac{\partial v}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) + k \frac{\partial u}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) \end{align}\] よって、 \[ \begin{align} \frac{f \left( \zeta \right) - f \left( z \right)}{\zeta - z} &= \frac{u \left( x+h, y+k \right) + i v \left( x+h, y+k \right) - u \left( x, y \right) - i v \left( x, y \right)}{h + ik} \\\\ &= \frac{1}{h+ik} \left\{ h \frac{\partial u}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) - k \frac{\partial v}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) \right\} \\\\ & \ \ \ \ \ + \frac{i}{h+ik} \left\{ h \frac{\partial v}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) + k \frac{\partial u}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) \right\} \\\\ &= \frac{\partial u}{\partial x} \left( x,y \right) + i \frac{\partial v}{\partial x} \left( x,y \right) \\\\ & \ \ \ \ \ + \frac{1}{h + ik} \left[ \left\{ \frac{\partial u}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) - \frac{\partial u}{\partial x} \left( x,y \right) \right\} h \right. \\\\ & \ \ \ \ \ \left. + i \left\{ \frac{\partial u}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) - \frac{\partial u}{\partial x} \left( x,y \right) \right\} k \right] \\\\ & \ \ \ \ \ + \frac{i}{h + ik} \left[ \left\{ \frac{\partial v}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) - \frac{\partial v}{\partial x} \left( x,y \right) \right\} h \right. \\\\ & \ \ \ \ \ \left. + i \left\{ \frac{\partial v}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) - \frac{\partial v}{\partial x} \left( x,y \right) \right\} k \right] \end{align}\] となる。\( \partial u / \partial x \) 、\( \partial v / \partial x \) がいずれも連続であることから、 \[ \begin{align} & \lim _{\zeta \to z} \frac{1}{h + ik} \left\{ \frac{\partial u}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) - \frac{\partial u}{\partial x} \left( x,y \right) \right\} h = 0 \\\\ & \lim _{\zeta \to z} \frac{i}{h + ik} \left\{ \frac{\partial u}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) - \frac{\partial u}{\partial x} \left( x,y \right) \right\} k = 0 \\\\ & \lim _{\zeta \to z} \frac{i}{h + ik} \left\{ \frac{\partial v}{\partial x} \left( x + \theta _2 h , y + \theta _2 k \right) - \frac{\partial v}{\partial x} \left( x,y \right) \right\} h = 0 \\\\ & \lim _{\zeta \to z} \frac{i^2}{h + ik} \left\{ \frac{\partial v}{\partial x} \left( x + \theta _1 h , y + \theta _1 k \right) - \frac{\partial v}{\partial x} \left( x,y \right) \right\} k = 0 \end{align}\] が成り立つため、 \[ \begin{align} f ' \left( z \right) = \lim _{\zeta \to z} \frac{f \left( \zeta \right) - f \left( z \right)}{\zeta - z} = \frac{\partial u}{\partial x} \left( x,y \right) + i \frac{\partial v}{\partial x} \left( x,y \right) \end{align}\] よって、\( f \left( z \right) \) は \( D \) の各点で複素微分可能であり、かつ、導関数 \( f ' \left( z \right) \) が \( D \) で連続であるため、\( f \left( z \right) \) は \( D \) で正則である。