目次
・曲線
・領域
・複素関数
カヤ
今回からしばらく一変数複素関数論について解説していく。
ナユミ
ほう。行列の話は前回のジョルダンの標準形で終わりってことかな？
カヤ
いや、最終的には行列の話にまた戻るつもりだが、一度ここで複素関数を取り扱わないと後で困るからな。
ナユミ
ふーん。そうなのね。わかったわ。
カヤ
じゃあまずは、曲線というものを定義しよう。
曲線
\[ 曲線\]
実区間 \( [a,b] \) を定義域とし、この実区間上で連続な実数値関数 \( x(t) \) 、\( y(t) \) により定義される複素数値関数
\[ \begin{align}
z(t) = x(t) + i y(t) \ \ \left( a \leq t \leq b \right) \ \ \ldots (1)
\end{align}\]
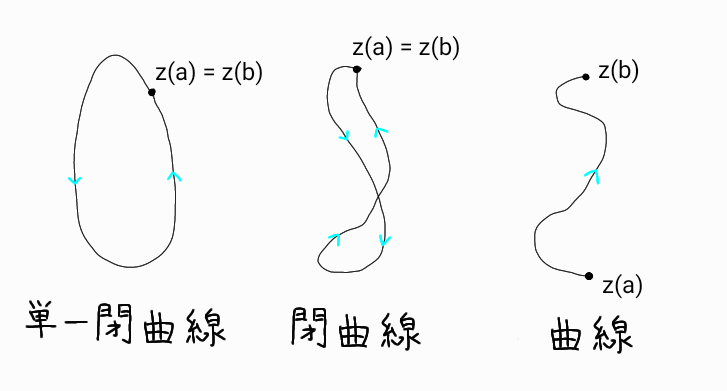
または、\( (1) \) を満たす複素平面上の点の集合 \( C \) を（連続）曲線と呼び、\( z(a) \) をその始点、\( z(b) \)
をその終点と呼ぶ。
特に、始点と終点が一致するとき、すなわち \( z(a) = z(b) \) が成り立つとき、その曲線を閉曲線と呼ぶ。
また、閉曲線において始点と終点以外に一致する 2 点が存在しないとき、その曲線は単一であると言う。
ナユミ
輪っかなら閉曲線。クロスしてない閉曲線は単一ね。
カヤ
そうだな。続いて、近傍、開集合、領域を定義しよう。
領域
\[ \begin{align}
近傍
\end{align}\]
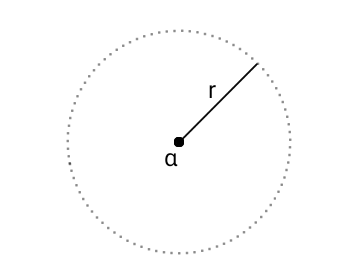
複素平面において、中心 \( \alpha \) 、半径 \( r \) の円の内部
\[ \begin{align}
U \left( \alpha , r \right) = \left\{ z | \left| z - \alpha \right| \lt r \right\}
\end{align}\]
を、点 \( \alpha \) の \( r \)-近傍と呼ぶ。
特に、半径を明記しない場合、単に点 \( \alpha \) の近傍と呼び、\( U \left( \alpha \right) \) と表す。
近傍は円の内部なので、円そのものは含みません。上の図では、円を破線で表すことでそのことを示しています。
続いて、開集合を次のように定義します。
続いて、開集合を次のように定義します。
\[ \begin{align}
開集合
\end{align}\]
複素平面における部分集合 \( D \) の任意の点 \( \alpha \) に対して、ある \( r \gt 0 \) が存在し、点 \( \alpha \) の \( r \)-近傍について
\[ \begin{align}
U \left( \alpha , r \right) \subset D
\end{align}\]
が成り立つとき、集合 \( D \) を開集合と呼ぶ。
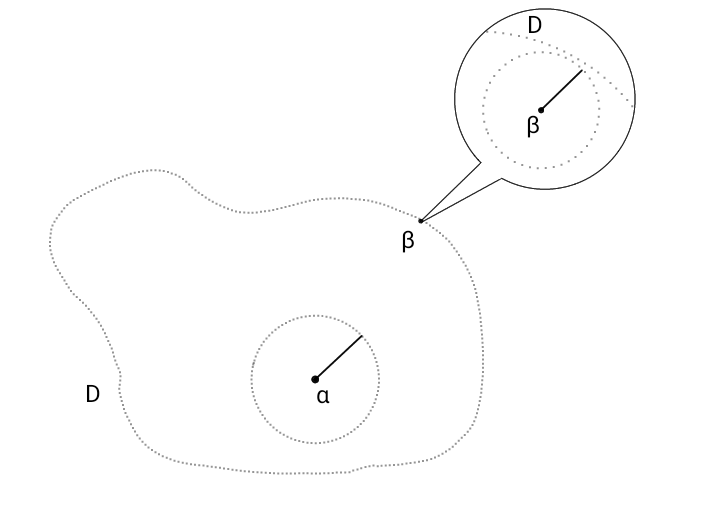
\( D \) が開集合であれば、\( D \) に含まれる任意の点は \( D \) に含まれる近傍を持つため、例えば上図の \( \beta \) のような \( D \)
の端にほとんど乗っているように見える点でも、拡大してみれば \( D \) に含まれる近傍があるということになります。
さらに言うと、開集合は境界を持たない集合とも言えます。
なぜなら、境界上の点を中心に円を描くと、どれだけ半径 \( r \) を小さく取っても、必ずどこかしらは \( D \) からはみ出す部分があるからです。
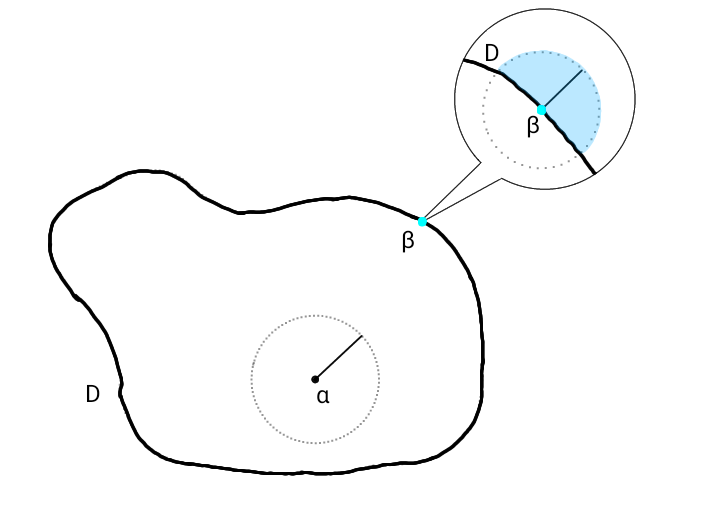
なお、複素平面 \( \mathbb C \) そのものは開集合です。
これは、任意の点 \( z_0 \in \mathbb C \) に対して、点 \( z_0 \) の \( r \)-近傍で
\[ \begin{align}
U \left( z_0 , r \right) \subset \mathbb C
\end{align}\]
を満たす \( r \) が存在するからです。
続いて、領域を次のように定義します。
続いて、領域を次のように定義します。
\[ \begin{align}
領域
\end{align}\]
複素平面における部分集合 \( D \) の任意の 2 点を \( D \) 内の連続曲線で結ぶことができるとき、\( D \) を弧状連結と呼ぶ。
弧状連結な開集合を領域と呼ぶ。
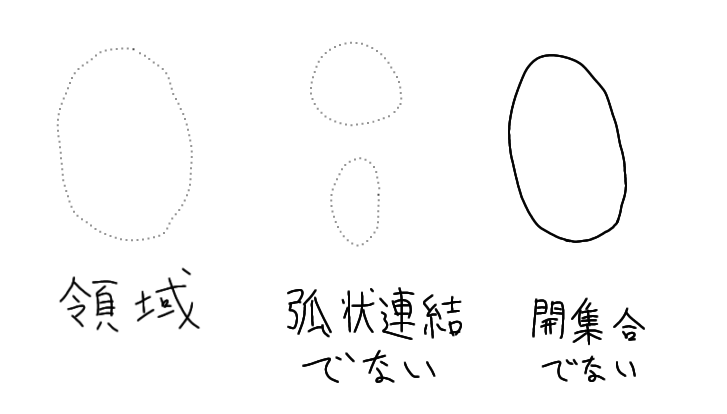
上図で領域と呼べるのは一番左の図だけです。
真ん中の図は弧状連結でないため領域ではなく、右端の図はそもそも開集合でないため領域ではありません。
ナユミ
話はわかったけど、何でこんな分類がいるの？
カヤ
それは、複素関数の正則性や複素積分に関わってくるが、まあ今はこういうものだと思っておいてくれ。
ナユミ
ふーん、まあ、そう思っておくわ。
カヤ
じゃあ最後に、複素関数を定義しよう。
複素関数
\[ \begin{align}
複素関数
\end{align}\]
複素平面における領域 \( D \) の各点 \( z \) に、複素数 \( w \) を対応させる関数
\[ \begin{align}
w = f(z) \ \ \left( z \in D \right)
\end{align}\]
を、\( D \) 上の複素関数と呼ぶ。
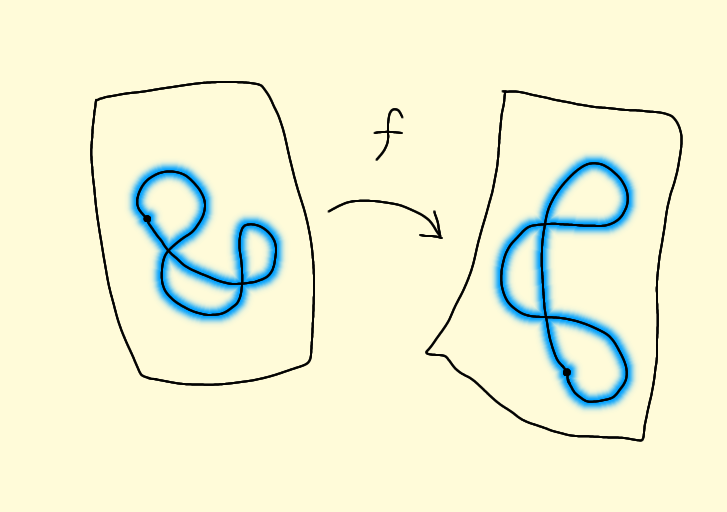
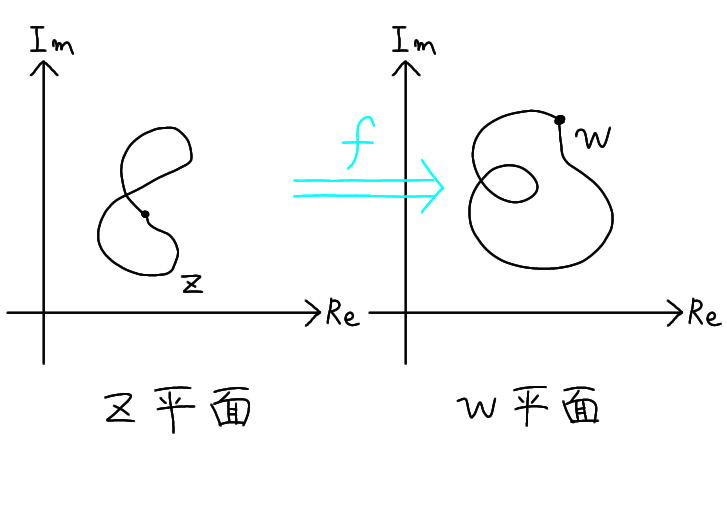
曲線 \( z \) が描かれる複素平面を \( z \) 平面、曲線 \( w \) が描かれる複素平面を \( w \) 平面と呼ぶことにすると、複素関数 \( w = f(z) \) は \( z \)
平面上の曲線 \( z \) を \( w \) 平面上の曲線 \( w \) に対応させる関数ともみなせます。
1 変数実数値関数と異なり、1 変数複素関数は \( z \) 平面上の実部と虚部の 2 つの値と、\( w \) 平面上の実部と虚部の 2 つの値を対応させることに注意します。
また、複素関数 \( w = f(z) \) は 2 変数実数値関数 \( u (x,y) \) 、\( v(x,y) \) を用いて、次のように実部と虚部に分けて表記することもあります。
\[ \begin{align}
z &= x + iy \\\\
w &= f(z) = u(x,y) + i v(x,y)
\end{align}\]
ナユミ
複素関数は 2 対 2 の対応なのね。
カヤ
そういうことだな。次回は具体的な複素関数を見ていく予定だ。
参考：
[1] 小寺 平治、テキスト複素解析、共立出版、2010年10月28日発行
前の記事
第46話
ジョルダンの標準形
ジョルダンの標準形
次の記事
第48話
複素関数の具体例
複素関数の具体例