目次
・一次分数関数
・複素指数関数
・三角関数
・対数関数
・指数関数
カヤ
今回は一変数複素関数の具体例について解説していく。が、各論に入る前に、一度手を動かしてグラフを描いてみよう。
\[ \begin{align}
T (z) = \frac{az+b}{cz+d} \quad \left( cz + d \neq 0 \right)
\end{align}\]
\[ \begin{align}
e^{z} = e^{x} \left( \cos y + i \sin y \right)
\end{align}\]
\[ \begin{align}
\cos z &= \frac{e^{iz} + e^{-iz}}{2}
\end{align}\]
\[ \begin{align}
\sin z &= \frac{e^{iz} - e^{-iz}}{2i}
\end{align}\]
\[ \begin{align}
\log z = \ln |z| + i \arg z \quad \left( z \neq 0 , \quad - \pi \lt \arg z \lt \pi \right)
\end{align}\]
\[ \begin{align}
a^z = e^{z \cdot \log a} = e^{z \cdot \left( \ln |a| + i \arg a \right)} \quad \left( a \neq 0 , \quad -
\pi \lt \arg a \lt \pi \right)
\end{align}\]
―説明書―
代表的な複素関数を描画するためのツールです。
初期設定では表示画面の左側に \( z \) 平面、右側に \( w \) 平面があります。 左側の \( z \) 平面上でマウスをドラックすると、\( z \) 平面上に曲線が描かれ、その曲線に対応した複素関数 \( w = f (z) \) の値が右側の \( w \) 平面上に描かれます。
\( z \) 平面の軸の最大値、および \( w \) 平面の軸の最大値を変更すると、それぞれの平面の軸の最大値が変わり、それに応じてグラフが拡大・縮小されます。
「関数」の設定を変えると、描画される複素関数の種類を変更できます。また、設定項目の4行目以降に選択した複素関数のパラメータの設定欄が表示され、その下には選択した複素関数の数式が表示されます。
\( z \) 平面プリセットでは、\( z \) 平面上に描く曲線のプリセットを選択できます。また、\( p \) を変更すると、プリセットで描く曲線の形状を変更できます。
グラフの種類を「|w|-arg w」に変えると、表示画面の左側に \( |w| \) が、右側に \( \arg w \) が表示されます。また、表示画面の下にはグラフの色と \( |w| \) および \( \arg w \) の値の対応図が表示されます。 ただし、\( -\pi \lt \arg w \lt \pi \) として表示しています。
代表的な複素関数を描画するためのツールです。
初期設定では表示画面の左側に \( z \) 平面、右側に \( w \) 平面があります。 左側の \( z \) 平面上でマウスをドラックすると、\( z \) 平面上に曲線が描かれ、その曲線に対応した複素関数 \( w = f (z) \) の値が右側の \( w \) 平面上に描かれます。
\( z \) 平面の軸の最大値、および \( w \) 平面の軸の最大値を変更すると、それぞれの平面の軸の最大値が変わり、それに応じてグラフが拡大・縮小されます。
「関数」の設定を変えると、描画される複素関数の種類を変更できます。また、設定項目の4行目以降に選択した複素関数のパラメータの設定欄が表示され、その下には選択した複素関数の数式が表示されます。
\( z \) 平面プリセットでは、\( z \) 平面上に描く曲線のプリセットを選択できます。また、\( p \) を変更すると、プリセットで描く曲線の形状を変更できます。
グラフの種類を「|w|-arg w」に変えると、表示画面の左側に \( |w| \) が、右側に \( \arg w \) が表示されます。また、表示画面の下にはグラフの色と \( |w| \) および \( \arg w \) の値の対応図が表示されます。 ただし、\( -\pi \lt \arg w \lt \pi \) として表示しています。
ナユミ
左に線を書くと、右にも対応する線が書かれるのね。でも、適当に書いててもなんだかよくわからないわ。
カヤ
複素関数のグラフを描くとはこういうものかと思ってもらえればまずは十分だよ。じゃあ、具体的にそれぞれの複素関数について見ていこう。
一次分数関数
以下では、\( x \) 、\( y \) を実数とし、\( i \) を虚数単位とします。
また、\( z = x + iy \) とし、\( z \) を独立変数とする複素関数を考えます。
なお、特別に記していない限り、定義域は \( z \in \mathbb C \) とします。
\[ \text{一次分数関数 } T (z) \]
\[ \begin{align}
T (z) = \frac{az+b}{cz+d} \quad \left( ad - bc \neq 0 \quad \text{かつ} \quad cz + d \neq 0 \right)
\end{align}\]
一次分数関数は一次変換またはメビウス変換とも呼ばれます。
\( ad - bc \neq 0 \) の条件は、\( T(z) \) が定数関数にならないためのもので、
\[ \begin{align}
T (z) = \frac{1}{c} \left( a - \frac{ad-bc}{cz+d} \right)
\end{align}\]
と変形したとき、かっこ内の第 2 項の分子が 0 にならないように指定されています。
定数 \( a \) 、\( b \) 、\( c \) 、\( d \) はいずれも複素数であるため、\( T(z) \) の実部と虚部を求めるには、次のように変形します。 \[ \begin{align} T(z) &= \frac{\left( \text{Re } a + i \cdot \text{Im } a \right) \left( x + iy \right) + \left( \text{Re } b + i \cdot \text{Im } b \right)}{\left( \text{Re } c + i \cdot \text{Im } c \right) \left( x + iy \right) + \left( \text{Re } d + i \cdot \text{Im } d \right)} \\\\ &= \frac{\left( x \cdot \text{Re } a - y \cdot \text{Im } a + \text{Re } b \right) + i \left( y \cdot \text{Re } a + x \cdot \text{Im } a + \text{Im } b \right)}{\left( x \cdot \text{Re } c - y \cdot \text{Im } c + \text{Re } d \right) + i \left( y \cdot \text{Re } c + x \cdot \text{Im } c + \text{Im } d \right)} \end{align}\] ここで、 \[ \begin{align} \alpha &= x \cdot \text{Re } a - y \cdot \text{Im } a + \text{Re } b \\\\ \beta &= y \cdot \text{Re } a + x \cdot \text{Im } a + \text{Im } b \\\\ \gamma &= x \cdot \text{Re } c - y \cdot \text{Im } c + \text{Re } d \\\\ \delta &= y \cdot \text{Re } c + x \cdot \text{Im } c + \text{Im } d \end{align}\] とおけば、 \[ \begin{align} T(z) &= \frac{\alpha + i \beta}{\gamma + i \delta} \\\\ &= \frac{\alpha \gamma + \beta \delta}{\gamma ^2 + \delta ^2} + i \frac{\beta \gamma - \alpha \delta}{\gamma ^2 + \delta ^2} \end{align}\] となり、\( T(z) \) の実部と虚部はいずれも \( \alpha \) 、\( \beta \) 、\( \gamma \) 、\( \delta \) を用いて表すことができます。
定数 \( a \) 、\( b \) 、\( c \) 、\( d \) はいずれも複素数であるため、\( T(z) \) の実部と虚部を求めるには、次のように変形します。 \[ \begin{align} T(z) &= \frac{\left( \text{Re } a + i \cdot \text{Im } a \right) \left( x + iy \right) + \left( \text{Re } b + i \cdot \text{Im } b \right)}{\left( \text{Re } c + i \cdot \text{Im } c \right) \left( x + iy \right) + \left( \text{Re } d + i \cdot \text{Im } d \right)} \\\\ &= \frac{\left( x \cdot \text{Re } a - y \cdot \text{Im } a + \text{Re } b \right) + i \left( y \cdot \text{Re } a + x \cdot \text{Im } a + \text{Im } b \right)}{\left( x \cdot \text{Re } c - y \cdot \text{Im } c + \text{Re } d \right) + i \left( y \cdot \text{Re } c + x \cdot \text{Im } c + \text{Im } d \right)} \end{align}\] ここで、 \[ \begin{align} \alpha &= x \cdot \text{Re } a - y \cdot \text{Im } a + \text{Re } b \\\\ \beta &= y \cdot \text{Re } a + x \cdot \text{Im } a + \text{Im } b \\\\ \gamma &= x \cdot \text{Re } c - y \cdot \text{Im } c + \text{Re } d \\\\ \delta &= y \cdot \text{Re } c + x \cdot \text{Im } c + \text{Im } d \end{align}\] とおけば、 \[ \begin{align} T(z) &= \frac{\alpha + i \beta}{\gamma + i \delta} \\\\ &= \frac{\alpha \gamma + \beta \delta}{\gamma ^2 + \delta ^2} + i \frac{\beta \gamma - \alpha \delta}{\gamma ^2 + \delta ^2} \end{align}\] となり、\( T(z) \) の実部と虚部はいずれも \( \alpha \) 、\( \beta \) 、\( \gamma \) 、\( \delta \) を用いて表すことができます。
ナユミ
うーん、この式の形からグラフの形を考えるのは難しいわね…
カヤ
そうだな。もう少し条件を簡単にして考えてみよう。
まずは、\( b = c = 0 \) 、\( d=1 \) の場合、つまり、
\[ \begin{align}
T(z) = az
\end{align}\]
について考えてみます。絶対値と偏角について、
\[ \begin{align}
& \left| T(z) \right| = |az| = |a||z| \\\\
& \arg T(z) = \arg \left( az \right) = \arg a + \arg z
\end{align}\]
が成り立つため、\( z \) 平面上の図形は \( w \) 平面上で \( |a| \) 倍に拡大され、\( \arg a \) だけ反時計回りに回転します。
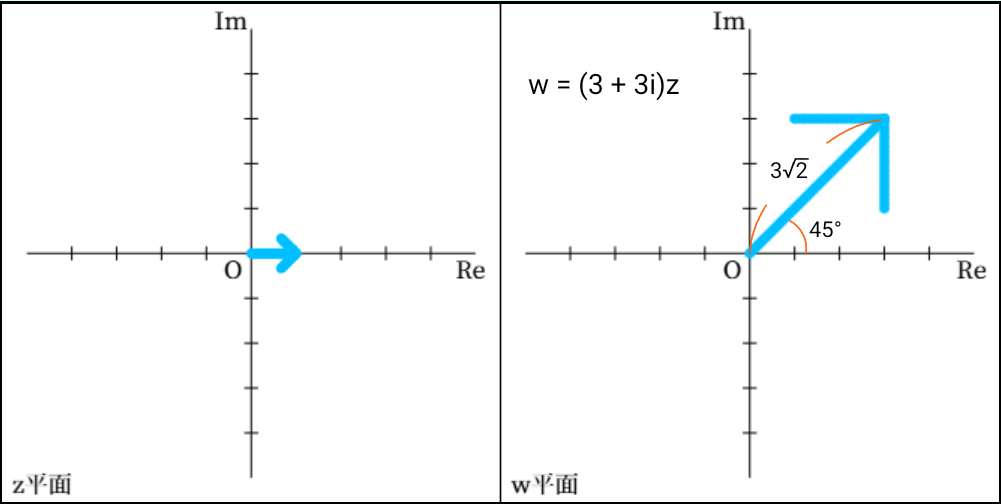
上の図は、\( z \) 平面上の原点から実軸上を右方向に 1 の長さだけ進んだ矢印が、複素関数
\[ \begin{align}
w = \left( 3 + 3i \right) z
\end{align}\]
によって \( w \) 平面上に写される様子を示しています。
\[ \begin{align}
& \left| 3 + 3i \right| = 3 \sqrt{2} \\\\
& \arg \left( 3 + 3i \right) = \frac{\pi}{4}
\end{align}\]
となることから、長さが \( 3 \sqrt{2} \) 倍された矢印が \( 45 ^ \circ \) 反時計回りに回転した形で写されています。
続いて、\( a = d = 1 \) 、\( c=0 \) の場合、つまり、 \[ \begin{align} T(z) = z + b \end{align}\] の場合を考えます。この場合、\( z \) 平面上の図形は実軸方向に \( \text{Re } b \) 、虚軸方向に \( \text{Im } b \) だけ平行移動した形で \( w \) 平面上に写されます。
最後に、\( b = c = 1 \) 、\( a=d=0 \) の場合、つまり、 \[ \begin{align} T(z) = \frac{1}{z} \end{align}\] の場合を考えます。絶対値と偏角について、 \[ \begin{align} & \left| T(z) \right| = \left|\frac{1}{z}\right| = \frac{1}{|z|} = \frac{|z|}{|z|^2} \\\\ & \arg T(z) = \arg \left( \frac{1}{z} \right) = \arg 1 - \arg z = - \arg z \end{align}\] が成り立つため、\( z \) 平面上の図形は \( w \) 平面上で \( 1/|z|^2 \) 倍に拡大され、\( \arg z \) だけ時計回りに回転します。
特別な場合の一例として、\( x = p \) のとき、\( T(z) = 1/z \) は \( w \) 平面上で半径 \( 1/2p \) 、中心 \( \left( 1/2p , 0 \right) \) の円を描きます。 下図は、\( x = 3/2 \) の場合を示しています。
続いて、\( a = d = 1 \) 、\( c=0 \) の場合、つまり、 \[ \begin{align} T(z) = z + b \end{align}\] の場合を考えます。この場合、\( z \) 平面上の図形は実軸方向に \( \text{Re } b \) 、虚軸方向に \( \text{Im } b \) だけ平行移動した形で \( w \) 平面上に写されます。
最後に、\( b = c = 1 \) 、\( a=d=0 \) の場合、つまり、 \[ \begin{align} T(z) = \frac{1}{z} \end{align}\] の場合を考えます。絶対値と偏角について、 \[ \begin{align} & \left| T(z) \right| = \left|\frac{1}{z}\right| = \frac{1}{|z|} = \frac{|z|}{|z|^2} \\\\ & \arg T(z) = \arg \left( \frac{1}{z} \right) = \arg 1 - \arg z = - \arg z \end{align}\] が成り立つため、\( z \) 平面上の図形は \( w \) 平面上で \( 1/|z|^2 \) 倍に拡大され、\( \arg z \) だけ時計回りに回転します。
特別な場合の一例として、\( x = p \) のとき、\( T(z) = 1/z \) は \( w \) 平面上で半径 \( 1/2p \) 、中心 \( \left( 1/2p , 0 \right) \) の円を描きます。 下図は、\( x = 3/2 \) の場合を示しています。
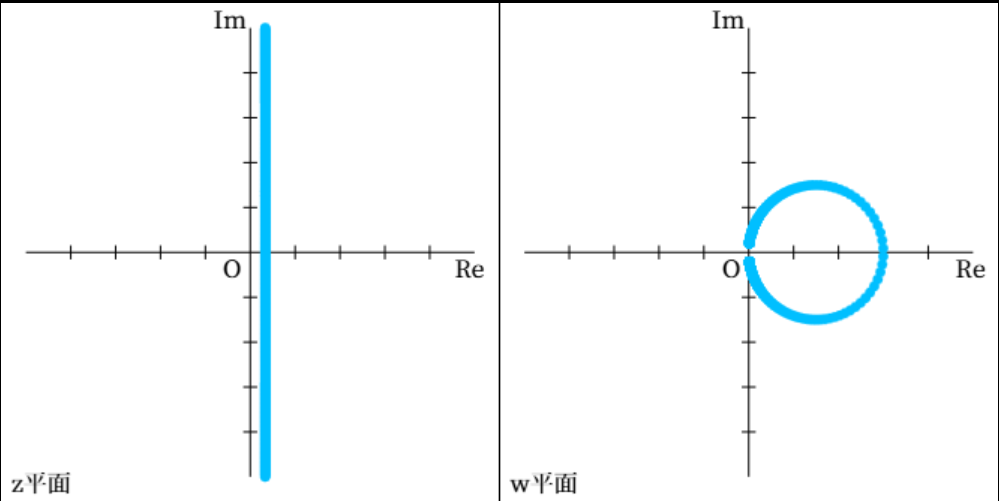
これが成り立つことを示すため、まず \( T(z) \) の実部と虚部を求めます。
\[ \begin{align}
T(z) &= \frac{1}{p + iy} \\\\
&= \frac{p - iy}{p^2 + y^2} \\\\
&= \frac{p}{p^2 + y^2} + i \frac{(-y)}{p^2 + y^2}
\end{align}\]
より、\( \text{Re } T(z) = u \) 、\( \text{Im } T(z) = v \) とすれば、
\[ \begin{align}
u &= \frac{p}{p^2 + y^2} \quad \ldots (1) \\\\
v &= - \frac{y}{p^2 + y^2} \quad \ldots (2)
\end{align}\]
となります。\( (2) \) 式より、
\[ \begin{align}
y^2 = - \frac{y}{v} - p^2
\end{align}\]
となるので、これを \( (1) \) 式に代入すると、
\[ \begin{align}
y = - \frac{pv}{u}
\end{align}\]
が得られます。これを \( (2) \) 式に代入すると、
\[ \begin{align}
v &= \frac{\left( pv/u \right)}{p^2 + \left( p^2 v^2/u^2 \right)} \\\\
p^2 + \frac{p^2 v^2}{u^2} &= \frac{p}{u} \\\\
p^2 u^2 + p^2 v^2 &= pu \\\\
p^2 u^2 - pu + p^2 v^2 &= 0 \\\\
u^2 - \frac{u}{p} + v^2 &= 0 \\\\
\left( u - \frac{1}{2p} \right) ^2 + v^2 &= \frac{1}{4p^2}
\end{align}\]
となります。最後の式は、\( w \) 平面上における半径 \( 1/2p \) 、中心 \( \left( 1/2p , 0
\right) \) の円の方程式を示しています。
よって、 \( x = p \) のとき、\( T(z) = 1/z \) は \( w \) 平面上で半径 \( 1/2p \) 、中心 \( \left( 1/2p , 0
\right) \) の円を描くことが示せました。
ナユミ
\( z \) 平面上の曲線によっては、見慣れた図形が出てきたりもするのね。
カヤ
そうだな。続いて、複素指数関数について見ていこう。
複素指数関数
\[ \begin{align}
\text{複素指数関数 } e^z
\end{align}\]
\[ \begin{align}
e^z = e^x \left( \cos y + i \sin y \right)
\end{align}\]
\( z \) が実数のときは \( e^z = e^x \) となり、複素指数関数は実数に対して定義された指数関数と一致します。
複素指数関数について、次の定理が成り立ちます。
\[ \begin{align}
&[1] \ e^{z_1} \cdot e^{z_2} = e^{z_1 + z_2} \\\\
&[2] \ \frac{e^{z_1}}{e^{z_2}} = e^{z_1 - z_2} \\\\
&[3] \ \left| e^z \right| = e^x, \quad \arg e^z = y \\\\
&[4] \ e^z \ \text{は周期 } 2 \pi i \ \text{の周期関数である。}
\end{align}\]
上記の 4 つの定理を順に証明していきます。
なお、以下の証明では、\( z_1 = x_1 + i y_1 \) 、\( z_2 = x_2 + i y_2 \) とします。
[1] の証明 \[ \begin{align} e^{z_1} \cdot e^{z_2} &= e^{x_1} \left( \cos y_1 + i \sin y_1 \right) \cdot e^{x_2} \left( \cos y_2 + i \sin y_2 \right) \\\\ &= e^{x_1 + x_2} \left\{ \cos y_1 \cos y_2 - \sin y_1 \sin y_2 + i \left( \sin y_1 \cos y_2 + \cos y_1 \sin y_2 \right) \right\} \\\\ &= e^{x_1 + x_2} \left\{ \cos \left( y_1 + y_2 \right) + i \sin \left( y_1 + y_2 \right) \right\} \\\\ &= e^{z_1 + z_2} \end{align}\]
[2] の証明
\[ \begin{align} \frac{e^{z_1}}{e^{z_2}} &= \frac{e^{x_1} \left( \cos y_1 + i \sin y_1 \right)}{e^{x_2} \left( \cos y_2 + i \sin y_2 \right)} \\\\ &= e^{x_1-x_2} \frac{\left( \cos y_1 + i \sin y_1 \right) \left( \cos y_2 - i \sin y_2 \right)}{\cos ^2 y_2 + \sin ^2 y_2} \\\\ &= e^{x_1-x_2} \left\{ \cos y_1 \cos y_2 + \sin y_1 \sin y_2 + i \left( \sin y_1 \cos y_2 - \cos y_1 \sin y_2 \right) \right\} \\\\ &= e^{x_1-x_2} \left\{ \cos \left( y_1 - y_2 \right) + i \sin \left( y_1 - y_2 \right) \right\} \\\\ &= e^{z_1-z_2} \end{align}\]
[3] の証明
\( e^z \) の極形式を考えればよいです。
[4] の証明
\[ \begin{align} e^{z+2 \pi i} &= e^z \cdot e^{2 \pi i} \\\\ &= e^z \cdot e^0 \left( \cos 2 \pi + i \sin 2 \pi \right) \\\\ &= e^z \end{align}\] 従って、\( e^z \) は周期 \( 2 \pi i \) の周期関数である。
\( x = p \) のとき、\( e^z \) が \( w \) 平面上に描く図形は、\( e^z \) の極形式を考えると \( \left| e^z \right| = e^p \) であることから、原点を中心とする半径 \( e^p \) の円になります。 また、\( y=p \) のときは、偏角が \( p \) となるため、原点から伸びた半直線になります。
[1] の証明 \[ \begin{align} e^{z_1} \cdot e^{z_2} &= e^{x_1} \left( \cos y_1 + i \sin y_1 \right) \cdot e^{x_2} \left( \cos y_2 + i \sin y_2 \right) \\\\ &= e^{x_1 + x_2} \left\{ \cos y_1 \cos y_2 - \sin y_1 \sin y_2 + i \left( \sin y_1 \cos y_2 + \cos y_1 \sin y_2 \right) \right\} \\\\ &= e^{x_1 + x_2} \left\{ \cos \left( y_1 + y_2 \right) + i \sin \left( y_1 + y_2 \right) \right\} \\\\ &= e^{z_1 + z_2} \end{align}\]
[2] の証明
\[ \begin{align} \frac{e^{z_1}}{e^{z_2}} &= \frac{e^{x_1} \left( \cos y_1 + i \sin y_1 \right)}{e^{x_2} \left( \cos y_2 + i \sin y_2 \right)} \\\\ &= e^{x_1-x_2} \frac{\left( \cos y_1 + i \sin y_1 \right) \left( \cos y_2 - i \sin y_2 \right)}{\cos ^2 y_2 + \sin ^2 y_2} \\\\ &= e^{x_1-x_2} \left\{ \cos y_1 \cos y_2 + \sin y_1 \sin y_2 + i \left( \sin y_1 \cos y_2 - \cos y_1 \sin y_2 \right) \right\} \\\\ &= e^{x_1-x_2} \left\{ \cos \left( y_1 - y_2 \right) + i \sin \left( y_1 - y_2 \right) \right\} \\\\ &= e^{z_1-z_2} \end{align}\]
[3] の証明
\( e^z \) の極形式を考えればよいです。
[4] の証明
\[ \begin{align} e^{z+2 \pi i} &= e^z \cdot e^{2 \pi i} \\\\ &= e^z \cdot e^0 \left( \cos 2 \pi + i \sin 2 \pi \right) \\\\ &= e^z \end{align}\] 従って、\( e^z \) は周期 \( 2 \pi i \) の周期関数である。
\( x = p \) のとき、\( e^z \) が \( w \) 平面上に描く図形は、\( e^z \) の極形式を考えると \( \left| e^z \right| = e^p \) であることから、原点を中心とする半径 \( e^p \) の円になります。 また、\( y=p \) のときは、偏角が \( p \) となるため、原点から伸びた半直線になります。
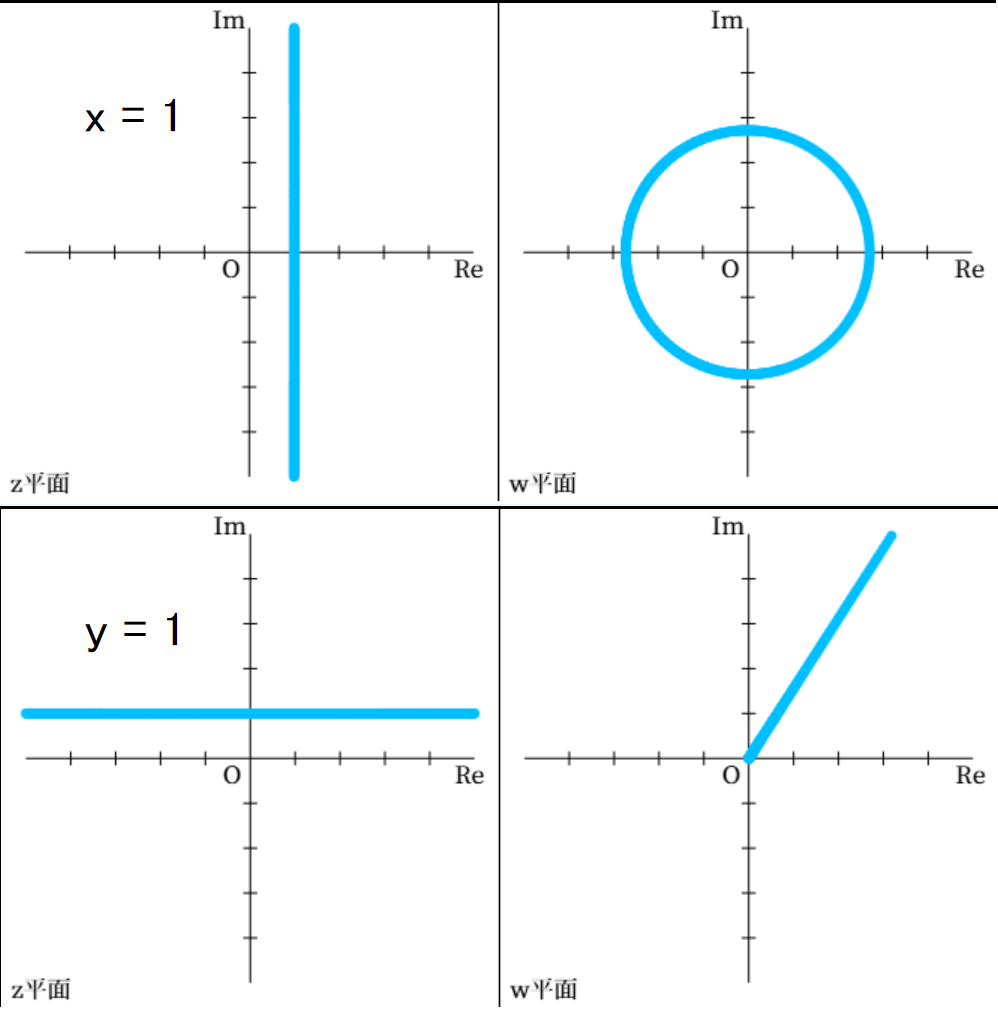
\( x=1 \) および \( y=1 \) のときの \( e^z \) による \( w \) 平面上のグラフ
ナユミ
普通の指数関数と似てるところもあるし、違うところもあるわね。
カヤ
混同しないように気を付けような。続いて、三角関数を見ていこう。
三角関数
\[ \begin{align}
三角関数
\end{align}\]
\[ \begin{align}
\cos z &= \frac{e^{iz} + e^{-iz}}{2} \\\\
\sin z &= \frac{e^{iz} - e^{-iz}}{2i}
\end{align}\]
実数を変数とする三角関数で成り立っていた公式の多くが上記の複素数を変数とする三角関数についても成り立ちます。
\[ \begin{align}
&[1] \sin ^2 z + \cos ^2 z = 1 \\\\
&[2] \sin \left( -z \right) = - \sin z , \quad \cos \left( -z \right) = \cos z \\\\
&[3] \sin \left( z_1 + z_2 \right) = \sin z_1 \cos z_2 + \cos z_1 \sin z_2 \\\\
&[4] \cos \left( z_1 + z_2 \right) = \cos z_1 \cos z_2 - \sin z_1 \sin z_2 \\\\
&[5] \cos z,\ \sin z \ \text{は周期 } 2 \pi \ \text{の周期関数である。}
\end{align}\]
上記の [1] ~ [5] の定理を順に証明していきます。
[1] の証明
\[ \begin{align} \sin ^2 z + \cos ^2 z &= \left( \frac{e^{iz} - e^{-iz}}{2i} \right) ^2 + \left( \frac{e^{iz} + e^{-iz}}{2} \right) ^2 \\\\ &= \frac{e^{2iz} -2 + e^{-2iz}}{4i^2} + \frac{e^{2iz} + 2 + e^{-2iz}}{4} \\\\ &= \frac{2 - e^{2iz} - e^{-2iz}}{4} + \frac{e^{2iz} + 2 + e^{-2iz}}{4} = 1 \end{align}\]
[2] の証明
\[ \begin{align} \sin \left( -z \right) &= \frac{e^{-iz} - e^{iz}}{2i} \\\\ &= - \left( \frac{e^{iz} - e^{-iz}}{2i} \right) = - \sin z \\\\\\ \cos \left( -z \right) &= \frac{e^{-iz} + e^{iz}}{2} = \cos z \end{align}\]
[3] の証明
\[ \begin{align} \sin z_1 \cos z_2 &= \frac{e^{iz_1} - e^{-iz_1}}{2i} \cdot \frac{e^{iz_2} + e^{-iz_2}}{2} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} + e^{i\left( z_1 - z_2\right)} - e^{i\left( z_2 - z_1\right)} - e^{-i\left( z_1 + z_2 \right)}}{4i} \\\\\\ \cos z_1 \sin z_2 &= \frac{e^{iz_1} + e^{-iz_1}}{2} \cdot \frac{e^{iz_2} - e^{-iz_2}}{2i} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} - e^{i\left( z_1 - z_2\right)} + e^{i\left( z_2 - z_1\right)} - e^{-i\left( z_1 + z_2 \right)}}{4i} \end{align}\] よって、 \[ \begin{align} \sin z_1 \cos z_2 + \cos z_1 \sin z_2 &= \frac{e^{i\left( z_1 + z_2 \right)} - e^{-i\left( z_1 + z_2 \right)}}{2i} \\\\ &= \sin \left( z_1 + z_2 \right) \end{align}\]
[4] の証明
\[ \begin{align} \cos z_1 \cos z_2 &= \frac{e^{iz_1} + e^{-iz_1}}{2} \cdot \frac{e^{iz_2} + e^{-iz_2}}{2} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} + e^{i\left( z_1 - z_2\right)} + e^{i\left( z_2 - z_1\right)} + e^{-i\left( z_1 + z_2 \right)}}{4} \\\\\\ \sin z_1 \sin z_2 &= \frac{e^{iz_1} - e^{-iz_1}}{2i} \cdot \frac{e^{iz_2} - e^{-iz_2}}{2i} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} - e^{i\left( z_1 - z_2\right)} - e^{i\left( z_2 - z_1\right)} + e^{-i\left( z_1 + z_2 \right)}}{4i^2} \\\\ &= \frac{-e^{i\left( z_1+z_2\right)} + e^{i\left( z_1 - z_2\right)} + e^{i\left( z_2 - z_1\right)} - e^{-i\left( z_1 + z_2 \right)}}{4} \end{align}\] よって、 \[ \begin{align} \cos z_1 \cos z_2 - \sin z_1 \sin z_2 &= \frac{e^{i\left( z_1 + z_2 \right)} + e^{-i\left( z_1 + z_2 \right)}}{2} \\\\ &= \cos \left( z_1 + z_2 \right) \end{align}\]
[5] の証明
\[ \begin{align} \cos \left( z + 2 \pi \right) &= \frac{e^{i\left( z + 2 \pi \right)} + e^{-i\left( z + 2 \pi \right)}}{2} \\\\ &= \frac{e^{iz} \cdot e^{2 \pi i} + e^{-iz} \cdot e^{-2 \pi i}}{2} \\\\ &= \frac{e^{iz} + e^{-iz}}{2} = \cos z \\\\\\ \sin \left( z + 2 \pi \right) &= \frac{e^{i\left( z + 2 \pi \right)} - e^{-i\left( z + 2 \pi \right)}}{2i} \\\\ &= \frac{e^{iz} \cdot e^{2 \pi i} - e^{-iz} \cdot e^{-2 \pi i}}{2i} \\\\ &= \frac{e^{iz} - e^{-iz}}{2i} = \sin z \end{align}\]
[1] の証明
\[ \begin{align} \sin ^2 z + \cos ^2 z &= \left( \frac{e^{iz} - e^{-iz}}{2i} \right) ^2 + \left( \frac{e^{iz} + e^{-iz}}{2} \right) ^2 \\\\ &= \frac{e^{2iz} -2 + e^{-2iz}}{4i^2} + \frac{e^{2iz} + 2 + e^{-2iz}}{4} \\\\ &= \frac{2 - e^{2iz} - e^{-2iz}}{4} + \frac{e^{2iz} + 2 + e^{-2iz}}{4} = 1 \end{align}\]
[2] の証明
\[ \begin{align} \sin \left( -z \right) &= \frac{e^{-iz} - e^{iz}}{2i} \\\\ &= - \left( \frac{e^{iz} - e^{-iz}}{2i} \right) = - \sin z \\\\\\ \cos \left( -z \right) &= \frac{e^{-iz} + e^{iz}}{2} = \cos z \end{align}\]
[3] の証明
\[ \begin{align} \sin z_1 \cos z_2 &= \frac{e^{iz_1} - e^{-iz_1}}{2i} \cdot \frac{e^{iz_2} + e^{-iz_2}}{2} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} + e^{i\left( z_1 - z_2\right)} - e^{i\left( z_2 - z_1\right)} - e^{-i\left( z_1 + z_2 \right)}}{4i} \\\\\\ \cos z_1 \sin z_2 &= \frac{e^{iz_1} + e^{-iz_1}}{2} \cdot \frac{e^{iz_2} - e^{-iz_2}}{2i} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} - e^{i\left( z_1 - z_2\right)} + e^{i\left( z_2 - z_1\right)} - e^{-i\left( z_1 + z_2 \right)}}{4i} \end{align}\] よって、 \[ \begin{align} \sin z_1 \cos z_2 + \cos z_1 \sin z_2 &= \frac{e^{i\left( z_1 + z_2 \right)} - e^{-i\left( z_1 + z_2 \right)}}{2i} \\\\ &= \sin \left( z_1 + z_2 \right) \end{align}\]
[4] の証明
\[ \begin{align} \cos z_1 \cos z_2 &= \frac{e^{iz_1} + e^{-iz_1}}{2} \cdot \frac{e^{iz_2} + e^{-iz_2}}{2} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} + e^{i\left( z_1 - z_2\right)} + e^{i\left( z_2 - z_1\right)} + e^{-i\left( z_1 + z_2 \right)}}{4} \\\\\\ \sin z_1 \sin z_2 &= \frac{e^{iz_1} - e^{-iz_1}}{2i} \cdot \frac{e^{iz_2} - e^{-iz_2}}{2i} \\\\ &= \frac{e^{i\left( z_1+z_2\right)} - e^{i\left( z_1 - z_2\right)} - e^{i\left( z_2 - z_1\right)} + e^{-i\left( z_1 + z_2 \right)}}{4i^2} \\\\ &= \frac{-e^{i\left( z_1+z_2\right)} + e^{i\left( z_1 - z_2\right)} + e^{i\left( z_2 - z_1\right)} - e^{-i\left( z_1 + z_2 \right)}}{4} \end{align}\] よって、 \[ \begin{align} \cos z_1 \cos z_2 - \sin z_1 \sin z_2 &= \frac{e^{i\left( z_1 + z_2 \right)} + e^{-i\left( z_1 + z_2 \right)}}{2} \\\\ &= \cos \left( z_1 + z_2 \right) \end{align}\]
[5] の証明
\[ \begin{align} \cos \left( z + 2 \pi \right) &= \frac{e^{i\left( z + 2 \pi \right)} + e^{-i\left( z + 2 \pi \right)}}{2} \\\\ &= \frac{e^{iz} \cdot e^{2 \pi i} + e^{-iz} \cdot e^{-2 \pi i}}{2} \\\\ &= \frac{e^{iz} + e^{-iz}}{2} = \cos z \\\\\\ \sin \left( z + 2 \pi \right) &= \frac{e^{i\left( z + 2 \pi \right)} - e^{-i\left( z + 2 \pi \right)}}{2i} \\\\ &= \frac{e^{iz} \cdot e^{2 \pi i} - e^{-iz} \cdot e^{-2 \pi i}}{2i} \\\\ &= \frac{e^{iz} - e^{-iz}}{2i} = \sin z \end{align}\]
ナユミ
加法定理とか、実変数よりこっちの方が証明楽なくらいね。
カヤ
指数法則で計算していけばいいだけだからな。あとは、特別な場合を見ておこう。
\( p \) を定数として、\( y = p \) であるとき、\( w = \cos z \) と \( w = \sin z \) はいずれも \( w \) 平面上に楕円を描きます。
ここでは、\( \cos z \) についてのみ、これを証明します。
\[ \begin{align} w = \cos z &= \cos \left( x + pi \right) \\\\ &= \cos x \cos pi - \sin x \sin pi \\\\ &= \cos x \cdot \frac{e^{-p} + e^{p}}{2} - \sin x \cdot \frac{e^{-p} - e^{p}}{2i} \\\\ &= \cos x \cdot \frac{e^{-p} + e^{p}}{2} + i \sin x \cdot \frac{e^{-p} - e^{p}}{2} \\\\ \end{align}\] よって、 \[ \begin{align} \text{Re } w = \cos x \cdot \frac{e^{-p} + e^{p}}{2} , \ \ \text{Im } w = \sin x \cdot \frac{e^{-p} - e^{p}}{2} \end{align}\] であり、 \[ \begin{align} \frac{\left( \text{Re } w \right)^2}{\left( \frac{e^{-p} + e^{p}}{2} \right)^2} + \frac{\left( \text{Im } w \right)^2}{\left( \frac{e^{-p} - e^{p}}{2} \right)^2} = \cos ^2 x + \sin ^2 x = 1 \end{align}\] が成り立ちます。これは、原点を中心とする楕円の式であるため、\( w \) 平面上には原点を中心とする楕円が描かれます。 この楕円と \( x \) 軸との交点の \( x \) 座標は \( \pm \left( e^{-p} + e^{p} \right) / 2 \) 、\( y \) 軸との交点の \( y \) 座標は \( \pm \left( e^{-p} - e^{p} \right)/2 \) です。
\[ \begin{align} w = \cos z &= \cos \left( x + pi \right) \\\\ &= \cos x \cos pi - \sin x \sin pi \\\\ &= \cos x \cdot \frac{e^{-p} + e^{p}}{2} - \sin x \cdot \frac{e^{-p} - e^{p}}{2i} \\\\ &= \cos x \cdot \frac{e^{-p} + e^{p}}{2} + i \sin x \cdot \frac{e^{-p} - e^{p}}{2} \\\\ \end{align}\] よって、 \[ \begin{align} \text{Re } w = \cos x \cdot \frac{e^{-p} + e^{p}}{2} , \ \ \text{Im } w = \sin x \cdot \frac{e^{-p} - e^{p}}{2} \end{align}\] であり、 \[ \begin{align} \frac{\left( \text{Re } w \right)^2}{\left( \frac{e^{-p} + e^{p}}{2} \right)^2} + \frac{\left( \text{Im } w \right)^2}{\left( \frac{e^{-p} - e^{p}}{2} \right)^2} = \cos ^2 x + \sin ^2 x = 1 \end{align}\] が成り立ちます。これは、原点を中心とする楕円の式であるため、\( w \) 平面上には原点を中心とする楕円が描かれます。 この楕円と \( x \) 軸との交点の \( x \) 座標は \( \pm \left( e^{-p} + e^{p} \right) / 2 \) 、\( y \) 軸との交点の \( y \) 座標は \( \pm \left( e^{-p} - e^{p} \right)/2 \) です。
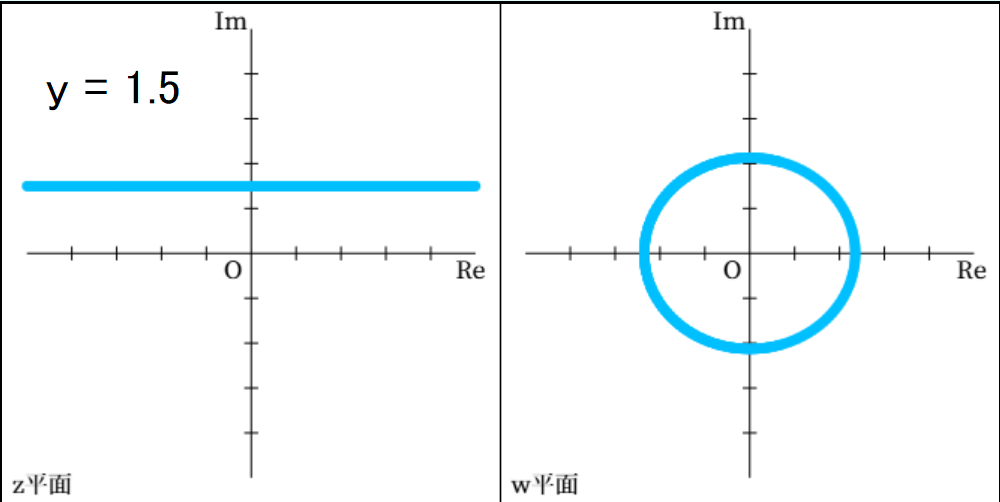
\( y=1.5 \) のときの \( \cos z \) による \( w \) 平面上のグラフ
一方、\( p \) を定数として、\( x = p \) であるとき、\( w = \cos z \) と \( w = \sin z \) はいずれも \( w \) 平面上に双曲線を描きます。
ここでは、\( \cos z \) についてのみ、これを証明します。
\[ \begin{align} w = \cos z &= \cos \left( p + iy \right) \\\\ &= \cos p \cos iy - \sin p \sin iy \\\\ &= \cos p \cdot \frac{e^{-y} + e^{y}}{2} - \sin p \cdot \frac{e^{-y} - e^{y}}{2i} \\\\ &= \cos p \cdot \frac{e^{-y} + e^{y}}{2} + i \sin p \cdot \frac{e^{-y} - e^{y}}{2} \\\\ \end{align}\] よって、 \[ \begin{align} \text{Re } w = \cos p \cdot \frac{e^{-y} + e^{y}}{2} , \ \ \text{Im } w = \sin p \cdot \frac{e^{-y} - e^{y}}{2} \end{align}\] であり、 \[ \begin{align} \frac{\left( \text{Re } w \right)^2}{\cos ^2 p} - \frac{\left( \text{Im } w \right)^2}{\sin ^2 p} &= \frac{\left( e^{-y} + e^{y} \right)^2}{4} - \frac{\left( e^{-y} - e^{y} \right)^2}{4} = 1 \end{align}\] が成り立ちます。これは、双曲線の式であるため、\( w \) 平面上には \( x \) 切片が \( \cos p \) である双曲線が描かれます。 ただし、\( \text{Re } w \) の符号は \( \cos p \) の符号で決まるため、双曲線は片側だけが描かれます。
\[ \begin{align} w = \cos z &= \cos \left( p + iy \right) \\\\ &= \cos p \cos iy - \sin p \sin iy \\\\ &= \cos p \cdot \frac{e^{-y} + e^{y}}{2} - \sin p \cdot \frac{e^{-y} - e^{y}}{2i} \\\\ &= \cos p \cdot \frac{e^{-y} + e^{y}}{2} + i \sin p \cdot \frac{e^{-y} - e^{y}}{2} \\\\ \end{align}\] よって、 \[ \begin{align} \text{Re } w = \cos p \cdot \frac{e^{-y} + e^{y}}{2} , \ \ \text{Im } w = \sin p \cdot \frac{e^{-y} - e^{y}}{2} \end{align}\] であり、 \[ \begin{align} \frac{\left( \text{Re } w \right)^2}{\cos ^2 p} - \frac{\left( \text{Im } w \right)^2}{\sin ^2 p} &= \frac{\left( e^{-y} + e^{y} \right)^2}{4} - \frac{\left( e^{-y} - e^{y} \right)^2}{4} = 1 \end{align}\] が成り立ちます。これは、双曲線の式であるため、\( w \) 平面上には \( x \) 切片が \( \cos p \) である双曲線が描かれます。 ただし、\( \text{Re } w \) の符号は \( \cos p \) の符号で決まるため、双曲線は片側だけが描かれます。
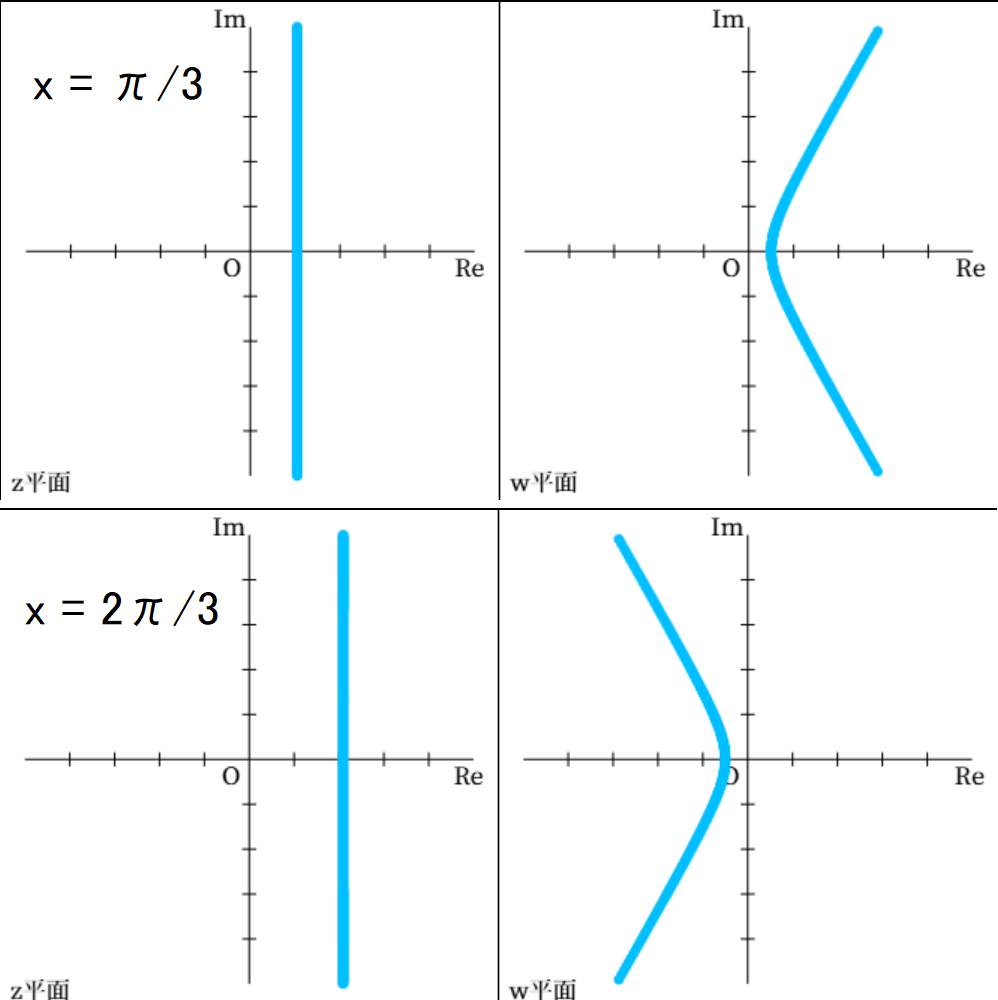
\( x= \pi / 3 , \ 2 \pi / 3 \) のときの \( \cos z \) による \( w \) 平面上のグラフ
ナユミ
二次曲線が現れるのね。
カヤ
そういうことだな。次は対数関数を見ていこう。
対数関数
\[ \begin{align}
対数関数
\end{align}\]
\[ \begin{align}
\log z = \ln |z| + i \arg z \quad \left( z \neq 0 , \quad - \pi \lt \arg z \lt \pi \right)
\end{align}\]
対数関数は複素指数関数 \( e^z \) の逆関数です。なぜなら、\( w = e^z = e^{x+iy}\) とすれば、
\[ \begin{align}
\ln |w| &= \ln e^x = x \\\\
\arg w &= y
\end{align}\]
となるため、
\[ \begin{align}
\log w = x + iy = z
\end{align}\]
を満たすからです。
ただし、\( w = e^z \) は周期関数であり、その周期は \( 2 \pi i \) です。
これは、\( \arg w \) が \( \pm 2 \pi\) されるごとに \( w \) は同じ値を返すことを意味します。
そのため、対数関数は一対一対応を保証するために、従属変数の偏角に制限を設けています。
特別な場合の一例として、\( z \) 平面上の原点中心の円 \[ \begin{align} z = r e^{i \theta} \ \ \left( r \ \text{は正の実数、} - \pi \lt \theta \lt \pi \right) \end{align}\] については、 \[ \begin{align} w = \log z = \ln r + i \theta \end{align}\] となるため、\( w \) 平面上に描かれる図形は実部が \( \ln r \) で固定され、虚部は \( - \pi \) から \( \pi \) まで動く直線となります。
特別な場合の一例として、\( z \) 平面上の原点中心の円 \[ \begin{align} z = r e^{i \theta} \ \ \left( r \ \text{は正の実数、} - \pi \lt \theta \lt \pi \right) \end{align}\] については、 \[ \begin{align} w = \log z = \ln r + i \theta \end{align}\] となるため、\( w \) 平面上に描かれる図形は実部が \( \ln r \) で固定され、虚部は \( - \pi \) から \( \pi \) まで動く直線となります。
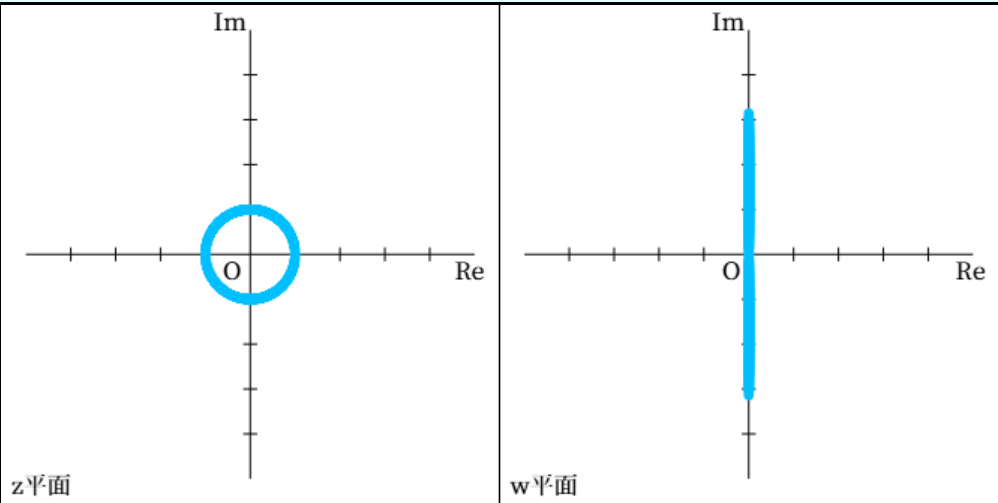
\( z = e^{i \theta} \) のときの \( \log z \) による \( w \) 平面上のグラフ
また、\( z \) 平面上の原点から伸びる半直線
\[ \begin{align}
z = \rho e^{i \phi} \ \ \left( \rho \gt 0 \ \text{、} \phi \ \text{は定数} \right)
\end{align}\]
については、
\[ \begin{align}
w = \log z = \ln \rho + i \phi
\end{align}\]
となります。\( w \) 平面上に描かれる図形は虚部が \( \phi \) で固定されるため、実軸に平行な直線になります。
カヤ
最後に、一般の指数関数を見ておこう。
指数関数
\[ 指数関数\]
\[ \begin{align}
a^z = e^{z \cdot \log a} = e^{z \cdot \left( \ln |a| + i \arg a \right)} \quad \left( a \neq 0 ,
\quad - \pi \lt \arg a \lt \pi \right)
\end{align}\]
指数関数は複素指数関数と対数関数を使って定義しています。
一対一対応を保証するために、底 \( a \) の偏角に制限を設けています。
また、
\[ \begin{align}
a^z &= e^{\left( x + iy \right) \left( \ln |a| + i \arg a \right)} \\\\
&= e^{\left( x \ln |a| - y \arg a \right) + i \left( y \ln |a| + x \arg a \right)}
\end{align}\]
と表せるため、
\[ \begin{align}
|a^z| &= e^{ x \ln |a| - y \arg a } \\\\
\arg a^z &= y \ln |a| + x \arg a
\end{align}\]
となります。
絶対値、偏角ともに \( x \) 、\( y \) に依存して変化しますが、\( x \) か \( y \) のいずれかを固定した場合、\( w \) 平面上には渦巻きが描かれます。
\( y \) を固定した場合、\( \ln |a| \) と \( \arg a \) が同符号であれば、中心から反時計回りに渦を巻きます。 一方、\( \ln |a| \) と \( \arg a \) が異符号であれば、中心から時計回りに渦を巻きます。
また、\( x \) を固定した場合、\( \ln |a| \) と \( \arg a \) が異符号であれば、中心から反時計回りに渦を巻きます。 一方、\( \ln |a| \) と \( \arg a \) が同符号であれば、中心から時計回りに渦を巻きます。
\( y \) を固定した場合、\( \ln |a| \) と \( \arg a \) が同符号であれば、中心から反時計回りに渦を巻きます。 一方、\( \ln |a| \) と \( \arg a \) が異符号であれば、中心から時計回りに渦を巻きます。
また、\( x \) を固定した場合、\( \ln |a| \) と \( \arg a \) が異符号であれば、中心から反時計回りに渦を巻きます。 一方、\( \ln |a| \) と \( \arg a \) が同符号であれば、中心から時計回りに渦を巻きます。
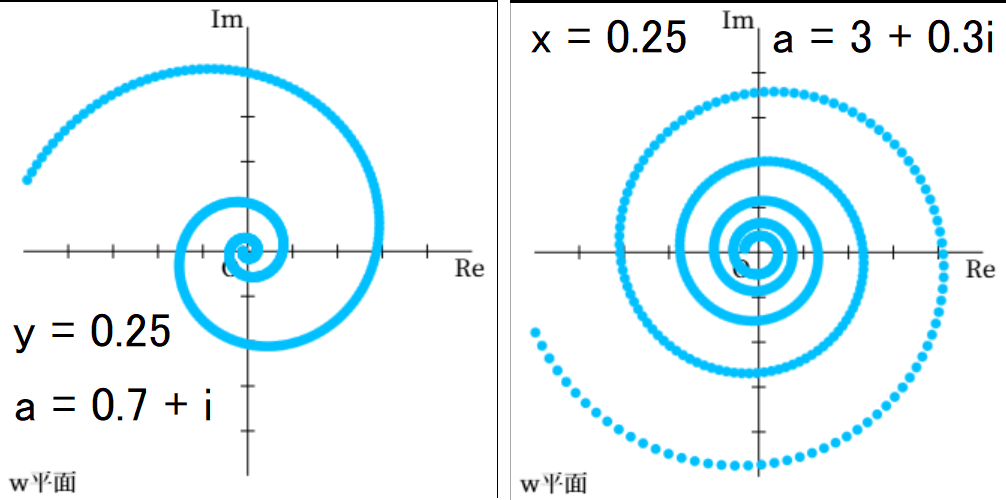
\( x \) あるいは \( y \) を定数としたときの \( a^z \) による \( w \) 平面上のグラフ
ナユミ
蚊取り線香みたいね。
カヤ
複素関数はいろいろな形のグラフが現れるからな。実際に描いてみるのが大事だな。
参考：
[1] 小寺 平治、テキスト複素解析、共立出版、2010年10月28日発行
[2] 岸 正倫・藤本担孝、複素関数論、学術図書出版社、1980年1月発行
前の記事
第47話
複素関数
複素関数
次の記事
第49話
ロルの定理・
平均値の定理
ロルの定理・
平均値の定理