第49話  ロルの定理・平均値の定理

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 6話

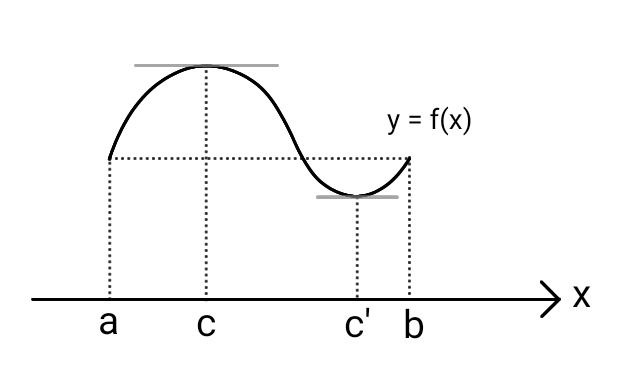
　ロルの定理、および次節で紹介する平均値の定理は「実数の連続性」と呼ばれる一連の命題の内の一つです。 これらの命題はいずれも同値であり、どれか一つを公理とすれば、他の命題はすべてそこから証明できるので、ここではロルの定理を公理としておきます。
　ロルの定理の主張は上図を見れば一目瞭然ですが、\( f'(c) = 0 \) を満たす \( c \) の個数は、\( f(x) \) の形によります。 ロルの定理が保証しているのは、\( f'(c) = 0 \) を満たす \( c \) が少なくとも一つある、つまり、\( f(x) \) の傾きが 0 になる箇所が少なくとも一つあるということだけで、いくつあるのか、どこにあるのかについては何も触れていない点には注意が必要です。

　以下、平均値の定理をロルの定理から証明していきます。

平均値の定理の証明： \[ \begin{align} A = \frac{f(b) - f(a)}{b-a} \end{align}\] として、次の関数 \[ \begin{align} g(x) = f(x) - Ax \end{align}\] を考えると、\( g(x) \) は \( [a,b] \) で連続、\( (a,b) \) で微分可能で、 \[ \begin{align} g(a) = g(b) = \frac{bf(a) - af(b)}{b-a} \end{align}\] を満たします。よって、ロルの定理より、 \[ \begin{align} g'(c) = f'(c) - A = 0 \end{align}\] となる点 \( c \ \left( a \lt c \lt b \right) \) が存在します。

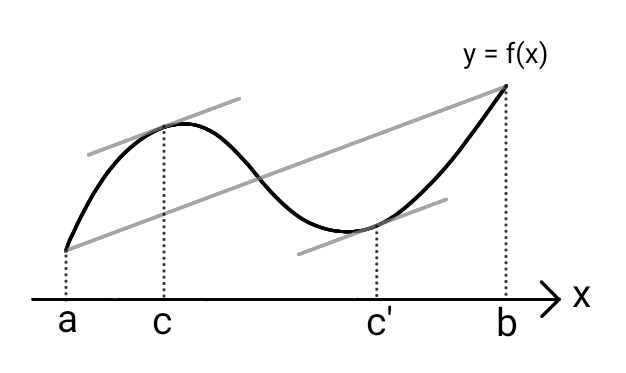
　平均値の定理もロルの定理と同じく、図で見たらわかりやすいです。

　また、平均値の定理を用いて、以前の記事で取り上げた次の定理を証明することができます。

証明： \( a \leq s \lt t \leq b \) となる \( s \) と \( t \) を任意に取ると、平均値の定理より、\( s \lt c \lt t \) を満たす \( c \) で、 \[ \begin{align} \frac{f(t)-f(s)}{t-s} = f'(c) = 0 \end{align}\] となるものが存在する。よって、\( f(t) = f(s) \) であり、\( s \) と \( t \) は任意であるから、\( f(x) \) は定数関数です。

証明：実数 \( r \) を次式が成り立つように定める： \[ \begin{align} f(b) = \sum _{k=0} ^{n-1} \frac{f^{\left( k \right)} (a)}{k!} \left( b-a \right)^{k} + \frac{r}{n!} \left( b-a \right)^n \end{align}\] 続いて、\( g(x) \) を次式で定義する。 \[ \begin{align} g(x) = f(b) - \left\{ \sum _{k=0} ^{n-1} \frac{f^{\left( k \right)} (x)}{k!} \left( b-x \right)^{k} + \frac{r}{n!} \left( b-x \right)^n \right\} \end{align}\] ここで、\( g(x) \) は \( \left[ a,b \right] \)（あるいは \( \left[ b,a \right] \) ）で連続で、\( \left( a,b \right) \)（あるいは \( \left( b,a \right) \) ）で微分可能であり、\( g(a) = g(b) \) を満たす。 よって、ロルの定理より、\( g'(c) = 0 \) となる \( c \)（ \( a \lt c \lt b \)（あるいは \( b \lt c \lt a \) ））が存在する。 上式より、積の微分公式および合成関数の微分公式を用いて \( g'(c) \) を計算すると、 \[ \begin{align} 0 &= g'(c) \\\\ &= - \sum _{k=0} ^{n-1} \frac{f^{\left( k +1 \right)} (c)}{k!} \left( b-c \right)^{k} + \left\{ \sum _{k=0} ^{n-2} \frac{f^{\left( k +1 \right)} (c)}{k!} \left( b-c \right)^{k} + \frac{r}{(n-1)!} \left( b-c \right)^{n-1} \right\} \\\\ &= - \frac{f^{\left( n \right)} (c)}{(n-1)!} \left( b-c \right)^{n-1} + \frac{r}{(n-1)!} \left( b-c \right)^{n-1} \end{align}\] ゆえに、\( r = f^{\left( n \right)} (c) \) が得られ、これを証明の始めの式に代入すればよい。


　テイラーの定理の式を、\( a=0 \) 、\( b = x \) 、\( c = \theta x \ \left( 0 \lt \theta \lt 1 \right)\) とおいて書き換えると、 \[ \begin{align} f(x) = \sum _{k=0} ^{n-1} \frac{f^{\left( k \right)} (0)}{k!} x^{k} + \frac{f^{\left( n \right)} (\theta x)}{n!} x^n \ \ldots (*) \end{align}\] となります。 \( a = 0 \) のときのテイラーの定理はマクローリンの定理と呼ばれることもあります。

　テイラーの定理およびマクローリンの定理の式にある、 \[ \begin{align} \frac{f^{\left( n \right)} (c)}{n!} \left( b-a \right)^n \ \ \ \text{または} \ \ \ \frac{f^{\left( n \right)} (\theta x)}{n!} x^n \end{align}\] の部分は、剰余項と呼びます。

★\( (1) \) の証明
　\( f(x) = e^x \) とすると、\( f ^{\left( n \right)} (x) = e^x \) であるから、\( f ^{\left( n \right)} (0) = e^0 = 1 \) となる。 これらをマクローリンの定理の式 \( (*) \) に代入すると、\( (1) \) 式を得る。


★\( (2) \) の証明
　\( f(x) = \sin x \) とすると、\( m = 0 , 1 , 2 , \ldots \) として、 \[ f ^{\left( n \right)} (x) = \begin{cases} \displaystyle \sin x & \left( n = 4m \right) \\[1em] \displaystyle \cos x & \left( n = 4m + 1 \right) \\[1em] \displaystyle - \sin x & \left( n = 4m + 2 \right) \\[1em] \displaystyle - \cos x & \left( n = 4m + 3 \right) \end{cases}\] となる。従って、 \[ f ^{\left( n \right)} (0) = \begin{cases} \displaystyle 0 & \left( n = 4m \right) \\[1em] \displaystyle 1 & \left( n = 4m + 1 \right) \\[1em] \displaystyle 0 & \left( n = 4m + 2 \right) \\[1em] \displaystyle -1 & \left( n = 4m + 3 \right) \end{cases}\] となり、\( n \) が偶数のとき、\( f ^{\left( n \right)} (0) = 0 \) である。 よって、マクローリンの定理の式 \( (*) \) に現れる \( n \) が偶数のときの項は無視してよく、\( k = 0 , 1 , 2 , \ldots \) として、 \[ \begin{align} f ^{\left( 2k+1 \right)} (x) &= \left( -1 \right)^k \cos x \\\\ f ^{\left( 2k+1 \right)} (0) &= \left( -1 \right)^k \end{align}\] と表せることから、\( (2) \) 式を得る。


★\( (3) \) の証明
　\( f(x) = \cos x \) とすると、\( m = 0 , 1 , 2 , \ldots \) として、 \[ f ^{\left( n \right)} (x) = \begin{cases} \displaystyle \cos x & \left( n = 4m \right) \\[1em] \displaystyle - \sin x & \left( n = 4m + 1 \right) \\[1em] \displaystyle - \cos x & \left( n = 4m + 2 \right) \\[1em] \displaystyle \sin x & \left( n = 4m + 3 \right) \end{cases}\] となる。従って、 \[ f ^{\left( n \right)} (0) = \begin{cases} \displaystyle 1 & \left( n = 4m \right) \\[1em] \displaystyle 0 & \left( n = 4m + 1 \right) \\[1em] \displaystyle -1 & \left( n = 4m + 2 \right) \\[1em] \displaystyle 0 & \left( n = 4m + 3 \right) \end{cases}\] となり、\( n \) が奇数のとき、\( f ^{\left( n \right)} (0) = 0 \) である。 よって、マクローリンの定理の式 \( (*) \) に現れる \( n \) が奇数のときの項は無視してよく、\( k = 0 , 1 , 2 , \ldots \) として、 \[ \begin{align} f ^{\left( 2k \right)} (x) &= \left( -1 \right)^k \cos x \\\\ f ^{\left( 2k \right)} (0) &= \left( -1 \right)^k \end{align}\] と表せることから、\( (3) \) 式を得る。


★\( (4) \) の証明
　\( f(x) = \ln (1+x) \) とすると、 \[ f ^{\left( n \right)} (x) = \begin{cases} \displaystyle \ln (1+x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( n = 0 \right) \\[1em] \displaystyle \left( -1 \right)^{n-1} \left( n-1 \right)! \left( \frac{1}{1+x} \right)^n \ \ \ \ \left( n \gt 0 \right) \end{cases}\] となる。従って、 \[ f ^{\left( n \right)} (0) = \begin{cases} \displaystyle 0 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( n = 0 \right) \\[1em] \displaystyle \left( -1 \right)^{n-1} \left( n-1 \right)! \ \ \ \ \left( n \gt 0 \right) \end{cases}\] となる。 これらをマクローリンの定理の式 \( (*) \) に代入すると、\( (4) \) 式を得る。


★\( (5) \) の証明
　\( f(x) = (1+x)^a \) とすると、 \[ f ^{\left( n \right)} (x) = \begin{cases} \displaystyle (1+x)^a \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( n = 0 \right) \\[1em] \displaystyle \left( \prod _{l=0} ^{n-1} (a-l) \right) \left( 1 + x \right)^{a-n} \ \ \ \ \left( n \gt 0 \right) \end{cases}\] となる。従って、 \[ f ^{\left( n \right)} (0) = \begin{cases} \displaystyle 1 \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( n = 0 \right) \\[1em] \displaystyle \prod _{l=0} ^{n-1} (a-l) \ \ \ \ \left( n \gt 0 \right) \end{cases}\] となる。 これらをマクローリンの定理の式 \( (*) \) に代入すると、\( (5) \) 式を得る。

証明： \( \sin x \) をマクローリンの定理により表すと、 \[ \begin{align} \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} + \cdots + (-1)^n \frac{\cos \theta x}{\left( 2n+1\right)!} x^{2n+1} \end{align}\] となる。よって、 \[ \begin{align} \frac{\sin x}{x} = 1 - \frac{x^2}{3!} + \frac{x^4}{5!} + \cdots + (-1)^n \frac{\cos \theta x}{\left( 2n+1\right)!} x^{2n} \end{align}\] ここで、剰余項については \( -1 \leq \cos \theta x \leq 1 \) であることにより、 \[ \begin{align} \lim _{x \to 0} \ (-1)^n \frac{\cos \theta x}{\left( 2n+1\right)!} x^{2n} = 0 \end{align}\] となる。従って、 \[ \begin{align} \lim _{x \to 0} \frac{\sin x}{x} = \lim _{x \to 0} \left\{ 1 - \frac{x^2}{3!} + \frac{x^4}{5!} + \cdots + (-1)^n \frac{\cos \theta x}{\left( 2n+1\right)!} x^{2n} \right\} = 1 \end{align}\] が成り立つ。