正弦波合成による楽音生成器

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 4話、 5話、 24話

―説明書―
　正弦波と余弦波を足し合わせて楽音を生成するシンセサイザです。
・表示画面下の設定項目について

　モード：「フリー」では表示画面上の鍵盤をクリックして音を鳴らせます。 「さくらさくら」ではさくらさくらを1回再生します。 「自動作曲」ではプログラムにより自動で作曲された曲が流れ続けます。

　音域：演奏される音の高さの範囲を選べます。

　音色：音色のプリセットを選べます。 音色は \( a_1 \) から \( a_{10} \) および \( b_1 \) から \( b_{10} \) のスライダーを動かしても変えられます。 スライダーの左端が -1 の値、右端が 1 の値、中央が 0 の値になっていて、0.02 ずつ値を変化させることができます。 表示画面左上の曲線は、音色の波形を示しています。

　包絡線：音圧の包絡線を選べます。 表示画面右上の曲線は、包絡線の形状を示しています。

　音はなんらかの媒質（固体、液体、気体）を伝わる波動で、これを音波と呼びます。 音波は通常下図のように、横軸に時間、縦軸に音圧をとったグラフで表されます。

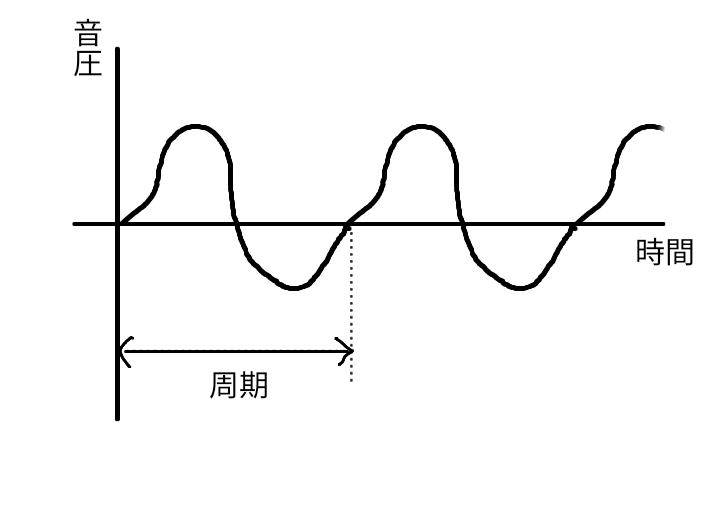
上図のように音波が明確な繰り返し構造を持つとき、1 回の繰り返しにかかる時間を周期と呼びます。 周期の逆数を振動数と呼び、ヘルツ（Hz）という単位をつけて表します。 ヒトの耳は 10 Hz - 20000 Hz までの音波を聴き取ることができるとされています。

　ピアノやギターなど、楽音の音波の形は様々ですが、 どんな形の音波であってもフーリエ級数を用いればそれを単純な正弦波（サイン）と余弦波（コサイン）の重ね合わせで表すことができます。 重ね合わさった音波のうち、最も振動数の低いものは基本振動数と呼ばれ、これが楽音の高さ（ピッチ）を決めています。 冒頭のシンセサイザでは次式で楽音の音波の形（音色）を決めています。 \[ \begin{align} \sum _{n=1} ^{10} \left( a_n \cos 2 \pi f n t + b_n \sin 2 \pi f n t \right) \ \ \ \ldots (*) \end{align}\] ただし、\( f \) は基本振動数です。 この式は 10 個の正弦波と 10 個の余弦波からなっていますが、フーリエ級数は無限個の正弦波および余弦波の足し合わせなので、この式であらゆる楽音の音波を表せるわけではないです。 足し合わせる正弦波と余弦波の個数を増やせばフーリエ級数により近づき、表せる波形の幅も広がりますが、無限個の足し合わせというのは実際にはできません。 そこで、何個足し合わせればいいのかという問題がありますが、これはヒトの耳が 20000 Hz までの音波を聴き取ることができると考えると、 \[ \begin{align} fn \leq 20000 \end{align}\] を満たす \( n \) までを取ればいいことになります。 例えば、基本振動数としてC3の音 \( \left( f = 130.813 \right) \) を取るなら、 \[ \begin{align} n \leq \frac{20000}{130.813} \cong 153 \end{align}\] となるので、正弦波と余弦波をそれぞれ 153 個足し合わせれば十分ということになります。 ただ、306 個のスライダーを操作するのは大変なので、上の式は 10 個ずつに留めてあるという次第です。

　三角関数の合成公式を用いると、\( (*) \) 式は次のように書き直せます。 \[ \begin{align} \sum _{n=1} ^{10} \sqrt{a_n ^2 + b_n ^2} \sin \left( 2 \pi f n t + \alpha _n \right) \ \ \ \ldots (*') \end{align}\] ただし、 \[ \begin{align} \cos \alpha _n &= \frac{a_n}{\sqrt{a_n ^2 + b_n ^2}} \\\\ \sin \alpha _n &= \frac{b_n}{\sqrt{a_n ^2 + b_n ^2}} \end{align}\] \( (*') \) 式から、フーリエ級数の式は正弦波のみの形にも書けるため、あらゆる音波は正弦波の重ね合わせで表現できるとも言うことができます。

　音色のプリセットには矩形波、三角波、鋸波という種類の波形がありますが、これらは元となる関数があってそれをフーリエ級数で表すことで得られます。 詳しい導出はここでは省略します。興味のある方は、数値実験 第21話にて解説している、偏微分方程式の初期条件からフーリエ係数を求めるところを参考にしてみてください。

　包絡線のパラメータは音圧の変化を制御するためのものです。 音が鳴っている間の音圧の変化は楽音の重要な構成要素で、例えばピアノ等の打鍵楽器は打鍵時に最大の音圧となり、その後速やかに音圧は減衰していきます。 シンセサイザの設定としては、右下がり 2 の設定が打鍵楽器をイメージしています。