TABLE OF CONTENTS
・About Radioactive Materials
・The Relationship Between Radioactivity and the Concentration of
Radioactive Materials
・Radiometric Dating

Nayumi
Hey, Kaya-chan. I saw on the news today that they're going to release treated water from the Fukushima
Daiichi nuclear plant into the ocean. Is that really safe?

Kaya
From what I’ve seen in the news, the concentration of radioactive substances is low enough that it
shouldn’t have much impact on people or marine life.

Nayumi
I see… But if they keep releasing the water over time, won’t the ocean eventually get filled with
radioactive stuff?

Kaya
You don’t need to worry about that. Radioactive materials break down over time, and their concentration
decreases. Let me explain a bit about how that works.
About Radioactive Materials

Kaya
First, let’s go over a few terms about radioactive materials.
\[ \text{Terms Related to Radioactive Materials}\]
Radiation: A general term for certain types of electromagnetic waves, atomic nuclei, and electrons
emitted during the decay of radioactive atoms.
Alpha \( ( \alpha ) \) radiation consists of helium nuclei.
Beta \( ( \beta ) \) radiation consists of electrons.
Gamma \( ( \gamma ) \) radiation is electromagnetic radiation with a wavelength between \( 10^{-14} \)
and \( 10^{-12} \) meters.
Radioactivity: The ability of a radioactive material to emit radiation. It is expressed in terms of the
number of radioactive atoms that decay per unit time. The standard unit is the becquerel (Bq), which
represents one decay per second.
Radioactive atom: An atom that possesses radioactivity.
Radioactive material: A substance that contains radioactive atoms.
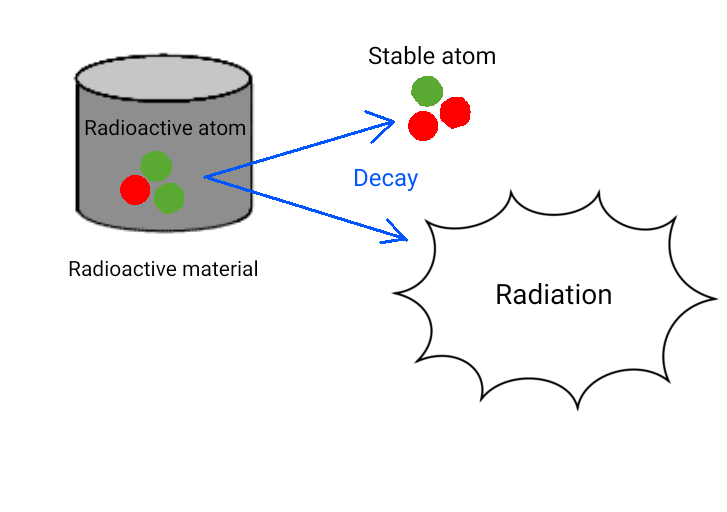
Radioactive atoms are unstable, so they decay in an attempt to become more stable atoms.
During this process, radiation is emitted.
Atoms are the basic particles that make up matter, consisting of a nucleus surrounded by electrons.
The nucleus itself is made up of protons and neutrons.
Different combinations of protons and neutrons give rise to different types of atoms. This can be
illustrated as follows:
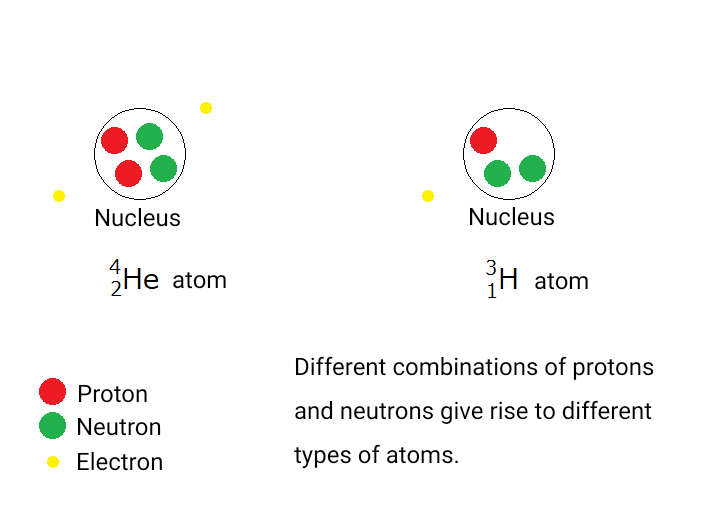
\( ^{4}_2 \rm He \) represents a helium atom, and \( ^{3}_{1} \rm H \) is tritium (also called hydrogen-3),
which is one of the substances found in the treated water released from the Fukushima nuclear plant.
\( \rm He \) is the chemical symbol for helium, and \( \rm H \) is the symbol for hydrogen.
Elements are categorized by the number of protons in their nuclei. Even when atoms have the same number of
protons, if they have different numbers of neutrons, they are called isotopes of the same element.
Among isotopes, those that possess radioactivity are called radioactive isotopes, or radioactive atoms.
For example, naturally occurring hydrogen has three isotopes, each with a different number of neutrons:
・Protium \( ^{1}_{1} \rm H \)
・Deuterium \( ^{2}_{1} \rm H \)
・Tritium \( ^{3}_{1} \rm H \)
Of these, tritium is a radioactive isotope.
Here, the number in the upper left of the element symbol indicates the total number of protons and neutrons
in the nucleus (called the mass number), while the number in the lower left indicates the number of protons
(the atomic number).

Nayumi
If we understand radioactivity, we might be able to figure out how long it takes for radioactive
materials to disappear.

Kaya
Exactly. Let's take a look at how we can use radioactivity to track changes in the concentration of
radioactive substances.
The Relationship Between Radioactivity and the Concentration of Radioactive Materials

Nayumi
What are the actual values of radioactivity like?

Kaya
Here’s a table showing the radioactivity levels of some radioactive isotopes released during the
Fukushima nuclear accident.
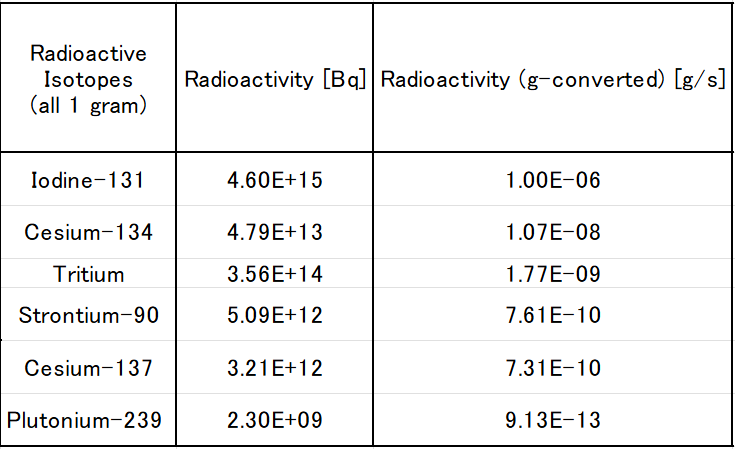
The values for radioactivity [Bq] are cited from the Wikipedia page “Comparison of radioactivity”(https://ja.wikipedia.org/wiki/放射能の比較).
The letter \( \rm E \) in the table represents scientific (exponential) notation.
・\( \rm E + \it x \) means \( \times 10^x \)
・\( \rm E - \it x \) means \( \times 10^{-x} \)
The values in the table show the radioactivity when exactly 1 gram of each radioactive isotope is present.
If the amount of the isotope is less than 1 gram due to decay over time, the actual radioactivity will also
be lower than the value listed.
The following equation expresses the relationship between radioactivity and the mass of the radioactive
isotope:
\[ ( \text{Radioactivity} ) = (\text{Decay constant}) \times (\text{Mass of the radioactive isotope}) \]
The decay constant is a value specific to each radioactive isotope.
When the mass of a radioactive isotope is exactly 1 gram, the decay constant is numerically equal to the
radioactivity, so the values in the previous table can also be interpreted as decay constants.
Radioactivity represents the number of radioactive atoms that decay per unit time.
This can also be understood as the decay rate of the radioactive isotope.
Therefore, the previous relationship can be rewritten as the following differential equation:
\[ \frac{dN}{dt} = - \lambda N\]
\( N \):Mass of the radioactive isotope、\( \lambda \):Decay constant、\( t \):Time
This is essentially the same as the differential equation in the Malthusian model, except for the negative
sign on the right-hand side.
Therefore, its solution is given as follows:
\[ N = N_0 e^{- \lambda t } \]
\( N_0 \):Initial mass
A graph of the radioactive isotopes from the earlier table would look like the one shown below.
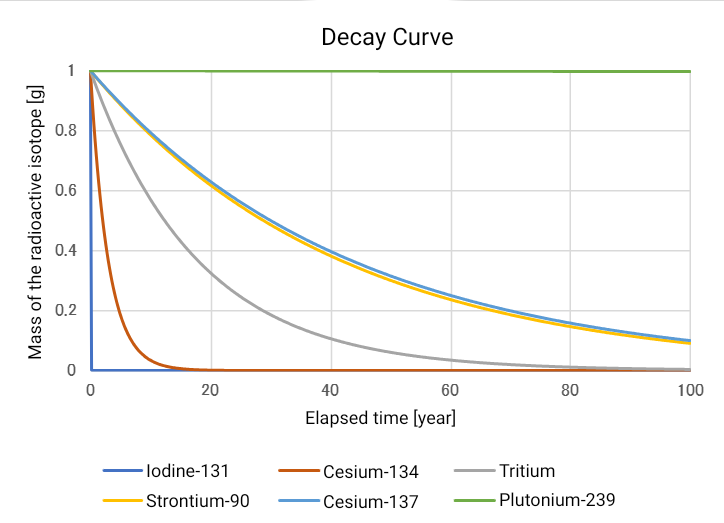
The decay of iodine-131 is rapid, and almost all of it disappears within a year.
However, this does not mean that any biological damage caused by the radiation emitted during its decay will
be repaired after one year.
What it means is that the substance iodine-131, which was released into the environment, will be nearly gone
after a year due to radioactive decay.
On the other hand, plutonium-239 decays extremely slowly — even after 100 years, most of it still
remains, so it requires long-term management and monitoring.
The decay constant determines how fast a radioactive isotope decays, but there is also a more intuitive
time-based indicator called the half-life.
The half-life is the time it takes for the mass of a radioactive isotope to decrease to half its original
amount due to decay.
For example:
・The half-life of iodine-131 is 8 days.
・The half-life of tritium (hydrogen-3) is 12.4 years.
The half-life can be calculated using the following formula:
Let \( T \) be the half-life, then
\[ \begin{align}
\frac{N_0}{2} &= N_0 e^{- \lambda T } \\\\
\frac{1}{2} &= e^{- \lambda T } \\\\
\ln \frac{1}{2} &= - \lambda T \\\\
- \ln 2 &= - \lambda T \\\\
T &= \frac{\lambda}{\ln 2}
\end{align}\]
As this equation shows, the half-life \( T \) is determined solely by the decay constant \( \lambda \) and
does not depend on the initial mass.
In other words, the half-life is a fixed value that depends on the type of radioactive isotope.
Among the radioactive isotopes released into the atmosphere during the Fukushima Daiichi nuclear
accident, cesium-137, which was released in relatively large quantities, has a half-life of approximately 30
years.
How much a radioactive substance must decay before people stop worrying about it may vary depending on the
individual,
but as long as we talk about a "half-life of 30 years," it is likely to be treated as a non-negligible issue
for at least that long.
In fact, even now—14 years after the accident—Japan’s Ministry of the Environment continues to monitor
radioactive substances annually in public water bodies and groundwater throughout the country.

Nayumi
Radioactive isotopes really are troublesome things...

Kaya
Yeah. From the perspective of pollution, the fact that some radioactive isotopes take a long time to
decay makes them a real problem. But that same property can actually be used in useful technologies.

Nayumi
Wait, really? There’s a technology like that?

Kaya
Yeah — it’s called radiometric dating.
Radiometric Dating

Nayumi
You mean like ruins and dinosaurs?

Kaya
Exactly — things like ancient ruins or dinosaurs.

Nayumi
How do they measure the age?

Kaya
There are different methods depending on what’s being measured, but for things like dinosaurs or
archaeological sites, radioactive carbon — \( ^{14} \rm C \), or carbon-14 — is often used.
\[ \text{Radiocarbon Dating Using} ^{14} \rm C \]
Living organisms, such as plants and animals, contain carbon \( \rm C \) in their bodies.
While they are alive, the ratio of radioactive carbon \( ^{14} \rm C \) to non-radioactive carbon \(
^{12} \rm C \) remains nearly constant.
This is because living organisms continuously exchange carbon with the environment through processes
like photosynthesis, respiration, eating, and excretion.
However, once an organism dies, this exchange stops. From that point on, the radioactive carbon \( ^{14}
\rm C \) inside its body begins to decay, while the amount of \( ^{12} \rm C \) remains unchanged.
As a result, the ratio of \( ^{14} \rm C \) to \( ^{12} \rm C \) gradually changes over time.
By measuring this changing ratio, scientists can determine how much time has passed since the
organism's death — in other words, they can estimate its age.
The chemist Willard Libby, who developed this dating method, was awarded the Nobel Prize in Chemistry in
1960 for his pioneering work.

Nayumi
That was a groundbreaking idea. So radioactive materials can actually be useful too.

Kaya
Yeah. And not just radioactive materials — we should remember that any chemical substance can bring
about good or harm, depending on how it's used.
References:
[1] 原子力百科事典 ATOMICA, https://atomica.jaea.go.jp/index.html, June 23,
2025
[2] 鵜沼英郎・尾形健明, 理工系基礎レクチャー 無機化学, 化学同人, April 1, 2007
[3] Wikipedia 放射能の比較, https://ja.wikipedia.org/wiki/放射能の比較, June 23, 2025
[4] 環境省HP 放射線による健康影響等に関する統一的な基礎資料(令和6年度版、 HTML形式) 第2章 放射線による被ばく 2.2 原子力災害, https://www.env.go.jp/chemi/rhm/current/02-02-04.html,
June 23, 2025
[5] 野口邦和, 放射性物質による生物及び人体への影響とその対応, 安全工学 Vol.50 No.6, 2011
[6] 環境省HP 放射性物質の常時監視 | 水環境における放射性物質の常時監視に関する評価検討会, https://www.env.go.jp/air/rmcm/conf_cm2.html,
June 23, 2025
[7] Wikipedia Radiocarbon dating, https://en.wikipedia.org/wiki/Radiocarbon_dating,
June 23, 2025
Previous

Ep. 1
Malthusian
Growth Model
Next
Ep. 3
Compound Interest






