TABLE OF CONTENTS
・The derivative of \( x^n \)
・The derivatives of trigonometric functions
・The derivatives of \( e^x \) and \( \ln x \)
・Logarithmic differentiation
・The derivatives of inverse trigonometric functions
・\( n \)th order derivative function
Mathematics articles that help in reading this article
・Numerical Computation： Ep. 1, Ep. 2, Ep. 4, Ep. 5, Ep. 6
・Numerical Computation： Ep. 1, Ep. 2, Ep. 4, Ep. 5, Ep. 6
Kaya
This time, let's introduce the differentiation of various functions. We'll start with the derivative of
\( x^n \) (where \( n \) is an integer).
The derivative of \( x^n \)
Nayumi
\( x^n \) means things like \( x \) or \( x^2 \)?
Kaya
That's the kind of function it is. Let's take a look at the formula first.
\[ \left( x^n \right) ' = n x^{n-1} \ \ ( n \ \text{is an integer,} \ x \ \text{is a real number} ) \]
The derivative of \( x^n \) is calculated by subtracting 1 from the exponent of \( x \) and then
multiplying by the original exponent.
To prove this formula, we first handle the case where \( n \gt 0 \), then move on to the case where \( n = 0
\).
Finally, we'll use these results to address the case where \( n \lt 0 \).
Let's start with the case where \( n \gt 0 \).
[1] When \( n = 1 \):
Since \( x^1 = x \), \[ \begin{align} (x)' &= \lim _{h \to 0} \frac{(x + h) - x}{h} \\\\ &= \lim _{h \to 0} \frac{h}{h} \\\\ &= \lim _{h \to 0} 1 \\\\ &= 1 \\\\ &= 1 \times x^{1-1} \\\\ \end{align} \] Therefore, when \( n = 1 \), the formula \( \left( x^n \right) ' = n x^{n-1} \) holds.
[2] Assume for any natural number \( k \), \[ \left( x^k \right) ' = k x^{k-1} \] holds. Then, for \( n = k+1 \) \[ \begin{align} (x^{k+1})' &= (x^k \times x)' \\\\ &= (x^k)' \times x + x^k \times (x)' \\\\ &= k x^{k-1} \times x + x^k \times 1 \\\\ &= k x^k + x^k \\\\ &= (k+1)x^k \\\\ &= (k+1)x^{(k+1)-1} \end{align} \] Thus, the formula \( \left( x^n \right) ' = n x^{n-1} \) also holds for \( n = k + 1\).
From [1] and [2], the formula \( \left( x^n \right) ' = n x^{n-1} \) holds for any natural number \( n \).
Since \( x^1 = x \), \[ \begin{align} (x)' &= \lim _{h \to 0} \frac{(x + h) - x}{h} \\\\ &= \lim _{h \to 0} \frac{h}{h} \\\\ &= \lim _{h \to 0} 1 \\\\ &= 1 \\\\ &= 1 \times x^{1-1} \\\\ \end{align} \] Therefore, when \( n = 1 \), the formula \( \left( x^n \right) ' = n x^{n-1} \) holds.
[2] Assume for any natural number \( k \), \[ \left( x^k \right) ' = k x^{k-1} \] holds. Then, for \( n = k+1 \) \[ \begin{align} (x^{k+1})' &= (x^k \times x)' \\\\ &= (x^k)' \times x + x^k \times (x)' \\\\ &= k x^{k-1} \times x + x^k \times 1 \\\\ &= k x^k + x^k \\\\ &= (k+1)x^k \\\\ &= (k+1)x^{(k+1)-1} \end{align} \] Thus, the formula \( \left( x^n \right) ' = n x^{n-1} \) also holds for \( n = k + 1\).
From [1] and [2], the formula \( \left( x^n \right) ' = n x^{n-1} \) holds for any natural number \( n \).
In [1], we showed that the formula holds when \( n = 1 \).
Next, in [2], we assumed the formula holds for \( n = k \) and then showed that it also holds for \( n = k +
1 \).
From this, we know the formula holds for \( n = 2 \) by combining [1] and [2]. Applying the same reasoning
again shows it holds for \( n = 3 \).
By continuing this process repeatedly, we can conclude that the formula holds for any natural number \( n
\).
This method of proof is generally called mathematical induction.
Nayumi
Now that we have proven the case for \( n \gt 0 \), next is the case when \( n = 0 \), right?
Kaya
That's right. The proof for \( n = 0 \) goes as follows.
When \( n = 0 \), \( x^0 = 1 \), then,
\[ \begin{align}
(1)' &= \lim _{h \to 0} \frac{1 - 1}{h} \\\\
&= \lim _{h \to 0} \frac{0}{h} \\\\
&= \lim _{h \to 0} 0 \\\\
&= 0 \\\\
&= 0 \times x^{0-1} \\\\
\end{align} \]
Therefore, when \( n = 0 \), the formula \( \left( x^n \right) ' = n x^{n-1} \) also holds.
The \( 1-1 \) in the numerator of the first line of the equation becomes easier to understand if you
consider the constant function \( f(x) = 1 \).
For this function, substituting \( x+h \) for the variable \( x \) still gives the value 1, so the numerator
of the derivative, \( f(x+h) - f(x) \), becomes \( 1-1 \).
At the end of the calculation, since multiplying zero by anything results in zero, we multiply by \( x^{0-1} \) to match the form of the formula.
At the end of the calculation, since multiplying zero by anything results in zero, we multiply by \( x^{0-1} \) to match the form of the formula.
Kaya
With this, we've proven the case for \( n \geq 0 \), so finally, let's prove the case where \( n \lt 0
\).
To prove that
\[ \left( x^n \right) ' = n x^{n-1} \]
holds for \( n \lt 0 \), it is sufficient to show that
\[ \left( x^{-m} \right) ' = -m x^{-m-1} \ \ \text{（} \ m \ \text{is a natural number）}\]
also holds.
\[ \begin{align}
\left( x^{-m} \right) ' &= \left( \frac{1}{x^m} \right) ' \\\\
&= \frac{(1)' \times x^{m} - 1 \times \left( x^m \right) '}{\left( x^m \right)^2} \\\\
&= \frac{0 \times x^{m} - 1 \times m x^{m-1}}{x^{2m}} \\\\
&= - \frac{m x^{m-1}}{x^{2m}} \\\\
&= - m x^{-m-1}
\end{align} \]
By substituting \( n = -m \), we can make use of the quotient rule for differentiation.
Nayumi
With this, we've proven that the derivative formula of \( x^n \) holds for all integers.
Kaya
That's right. Next, let's move on to the differentiation of trigonometric functions.
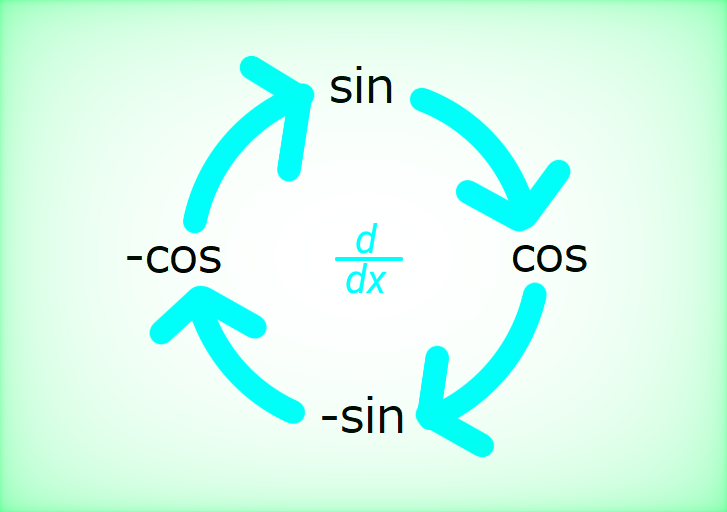
The derivatives of trigonometric functions
\[ \begin{align}
&\left( \sin x \right) ' = \cos x \ \ (x \ \rm is \ real.) \\\\
&\left( \cos x \right) ' = - \sin x \ \ (x \ \rm is \ real.) \\\\
&\left( \tan x \right) ' = \frac{1}{\cos ^2 x} \ \ (\rm Where \ \ \it x \ \ \rm is \ a \ real \ number \
except \ \frac{(2 \it n \rm -1) \pi}{2} \ \rm in \ which \ \it n \ \rm is \ an \ integer.)
\end{align} \]
\[ \tan x = \frac{\sin x}{\cos x} \]
This definition holds only when \( \cos x \neq 0 \).
Therefore, if \( n \) is an integer,
\[ x = \frac{(2 \it n \rm -1) \pi}{2} \]
makes the derivative of the tangent function undefined.
Kaya
Let's start by proving the derivative of \( \sin x \).
\[ \begin{align}
\left( \sin x \right) ' &= \lim _{h \to 0} \frac{\sin \left( x+h \right) - \sin x}{h} \\\\
&= \lim _{h \to 0} \frac{2 \cos \frac{\left( x+h \right) + x}{2} \sin \frac{\left( x+h \right) -
x}{2}}{h} \\\\
&= \lim _{h \to 0} \frac{2 \cos \frac{2x+h}{2} \sin \frac{h}{2}}{h} \\\\
&= \lim _{h \to 0} 2 \cos \frac{2x+h}{2} \frac{\sin \frac{h}{2}}{\frac{h}{2}} \times \frac{1}{2} \\\\
&= 2 \cos \frac{2x}{2} \times 1 \times \frac{1}{2} \\\\
&= \cos x
\end{align} \]
In the second line, we used the identity that rewrites a difference as a product.
In the fourth line, we arranged the expression to apply the sinc function limit formula:
\[ \lim _{x \to 0} \frac{\sin x}{x} = 1 \]
Nayumi
Next, let's move on to the derivative of \( \cos x \).
\[ \begin{align}
\left( \cos x \right) ' &= \lim _{h \to 0} \frac{\cos \left( x+h \right) - \cos x}{h} \\\\
&= \lim _{h \to 0} - \frac{2 \sin \frac{\left( x+h \right) + x}{2} \sin \frac{\left( x+h \right) -
x}{2}}{h} \\\\
&= \lim _{h \to 0} - \frac{2 \sin \frac{2x+h}{2} \sin \frac{h}{2}}{h} \\\\
&= \lim _{h \to 0} - 2 \sin \frac{2x+h}{2} \frac{\sin \frac{h}{2}}{\frac{h}{2}} \times \frac{1}{2} \\\\
&= - 2 \sin \frac{2x}{2} \times 1 \times \frac{1}{2} \\\\
&= - \sin x
\end{align} \]
Nayumi
The process is similar to the derivative of \( \sin x \).
Kaya
Exactly. For the derivative of \( \tan x \), let's use the quotient rule.
\[ \begin{align}
\left( \tan x \right) ' &= \left( \frac{\sin x}{\cos x} \right) ' \\\\
&= \frac{\left( \sin x \right)' \cos x - \sin x \left( \cos x \right) '}{\cos ^2 x} \\\\
&= \frac{\cos x \cos x - \sin x \left( - \sin x \right) }{\cos ^2 x} \\\\
&= \frac{\cos ^2 x + \sin ^2 x}{\cos ^2 x} \\\\
&= \frac{1}{\cos ^2 x}
\end{align} \]
Nayumi
The last step used the identity
\[ \sin ^2 x + \cos ^2 x = 1\]
right?
Kaya
That's right. That concludes the differentiation of trigonometric functions. Next, we'll move on to the
differentiation of the exponential function with base \( e \), \( e^x \), and the natural logarithm
function, \( \ln x \).
The derivatives of \( e^x \) and \( \ln x \)
Kaya
Before diving into the differentiation formulas, let's explain the following two limit formulas.
\[ \lim _{x \to 0} \frac{e^x - 1}{x} = 1 \]
\[ \lim _{x \to 0} \left( 1+x \right) ^{\frac{1}{x}} = e \]
Nayumi
There are two of them, right?
Kaya
Yes. The lower formula can be easily derived from the upper one.
\[ \begin{align}
\lim _{x \to 0} \frac{e^x - 1}{x} &= 1 \\\\
\lim _{x \to 0} e^x - 1 &= \lim _{x \to 0} x \\\\
\lim _{x \to 0} e^x &= \lim _{x \to 0} \left( 1+x \right) \\\\
e &= \lim _{x \to 0} \left( 1+x \right) ^{\frac{1}{x}}
\end{align} \]
Nayumi
I see. Then how do we derive the upper formula?
Kaya
The upper formula can be derived by using the property of \( e^x \) that its tangent line at \( x = 0 \)
has a slope of 1.
For \( f(x) = e^x \), the slope of the tangent line at \( x = 0 \), which is the derivative at that
point, is 1. Therefore,
\[ \begin{align}
f'(0) &= \lim _{h \to 0} \frac{f \left( 0 + h \right) - f(0)}{h} \\\\
&= \lim _{h \to 0} \frac{e^{0+h} - e^0}{h} \\\\
&= \lim _{h \to 0} \frac{e^{h} - 1}{h} \\\\
&= \lim _{x \to 0} \frac{e^{x} - 1}{x} = 1
\end{align} \]
Nayumi
You replaced the slope of the tangent with the derivative, right?
Kaya
Exactly. Now that we've derived the limit formula, let's move on to the differentiation formulas.
\[ \begin{align}
&\left( e^x \right) ' = e^x \ \ ( x \ \rm{is \ real.} ) \\\\
&\left( \ln x \right) ' = \frac{1}{x} \ \ ( x \rm \gt 0 )
\end{align} \]
Nayumi
The derivative of \( e^x \) just stays the same, right?
Kaya
Exactly. Let's start by finding the derivative of \( e^x \).
\[ \begin{align}
\left( e^x \right) ' &= \lim _{h \to 0} \frac{e^{x+h} - e^x}{h} \\\\
&= \lim _{h \to 0} \frac{e^x e^h - e^x}{h} \\\\
&= \lim _{h \to 0} \frac{e^{x} \left( e^h - 1 \right) }{h} \\\\
&= e^{x} \lim _{h \to 0} \frac{e^h - 1}{h} \\\\
&= e^{x} \times 1 = e^x
\end{align} \]
In the fourth line, \( e^x \), which does not depend on \( h \), is taken outside the limit, creating a
form where the previously derived limit formula can be applied.
Nayumi
Easy to remember, since it stays the same even after differentiation.
Kaya
Exactly. Next, the derivative of \( \ln x \) is as follows.
\[ \begin{align}
\left( \ln x \right) ' &= \lim _{h \to 0} \frac{\ln \left( x+h \right) - \ln x}{h} \\\\
&= \lim _{h \to 0} \frac{\ln \frac{x+h}{x}}{h} \\\\
&= \lim _{h \to 0} \frac{1}{h} \ln \left( 1 + \frac{h}{x} \right) \\\\
&= \lim _{h \to 0} \ln \left( 1 + \frac{h}{x} \right) ^{\frac{1}{h}} \\\\
&= \lim _{h \to 0} \ln \left\{ \left( 1 + \frac{h}{x} \right) ^{\frac{x}{h}} \right\} ^{\frac{1}{x}}
\\\\
&= \ln e^{\frac{1}{x}} \\\\
&= \frac{1}{x} \ln e = \frac{1}{x}
\end{align} \]
Nayumi
It's a full parade of exponent and logarithm rules. The step from the fourth to the fifth line isn't
something you'd think of right away.
Kaya
Yeah, it was a pretty technical manipulation. Next, let's explain logarithmic differentiation, which
uses this derivative of \( \ln x \).
Logarithmic differentiation
Nayumi
You use logarithms for differentiation, right?
Kaya
Exactly. Let me introduce two formulas that can be derived using this logarithmic differentiation
method.
\[ \left( x^a \right) ' = a x^{a-1} \ \ ( a \ \rm{is} \ \rm{real, \ and} \ \it{x} \ \rm{is \ a \
positive \ real \ number.} )\]
\[ \left( a^x \right) ' = a^x \ln a \ \ ( x \ \rm{is \ real, \ and} \ \it{a} \ \rm{is \ a \ positive \
real \ number.} ) \]
The first one has the same form as the derivative of \( x^n \) we found earlier.
However, note that the exponent has been extended from integers to real numbers, and the domain is
restricted to positive real numbers.
Kaya
First, let's derive the upper formula.
Let \( y = x^a \), and take the natural logarithm of both sides:
\[ \begin{align}
\ln y &= \ln x^a \\\\
\ln y &= a \ln x
\end{align} \]
Differentiating both sides with respect to \( x \):
\[ \begin{align}
\frac{d}{dx} \left( \ln y \right) &= \frac{d}{dx} \left( a \ln x \right) \\\\
\end{align} \]
Now, if we set \( v = \ln y \), then by the chain rule, the left-hand side becomes:
\[ \begin{align}
\frac{d}{dx} \left( \ln y \right) &= \frac{dv}{dx} \\\\
&= \frac{dv}{dy} \frac{dy}{dx} \\\\
&= \left( \ln y \right) ' y' \\\\
&= \frac{1}{y} y'
\end{align} \]
Thus,
\[ \begin{align}
\frac{1}{y} y' &= \frac{d}{dx} \left( a \ln x \right) \\\\
\frac{1}{y} y' &= a \frac{d}{dx} \left( \ln x \right) \\\\
\frac{1}{y} y' &= \frac{a}{x} \\\\
y' &= \frac{a}{x} \times y \\\\
&= \frac{a}{x} x^a = a x^{a-1}
\end{align} \]
We used the derivative notation \( \frac{d}{dx} \), which is especially useful when dealing with three or
more variables, as it clearly indicates with respect to which variable the differentiation is performed.
Also, since logarithmic differentiation starts by taking the natural logarithm, be careful that it can only
be applied to functions whose values are positive real numbers.
Nayumi
Next, let's derive the other formula.
Let \( y = a^x \), and take the natural logarithm of both sides:
\[ \begin{align}
\ln y &= \ln a^x \\\\
\ln y &= x \ln a
\end{align} \]
Differentiating both sides with respect to \( x \):
\[ \begin{align}
\frac{d}{dx} \left( \ln y \right) &= \frac{d}{dx} \left( x \ln a \right) \\\\
\end{align} \]
Now, if we set \( v = \ln y \), then by the chain rule, the left-hand side becomes:
\[ \begin{align}
\frac{d}{dx} \left( \ln y \right) &= \frac{1}{y} y'
\end{align} \]
Thus,
\[ \begin{align}
\frac{1}{y} y' &= \frac{d}{dx} \left( x \ln a \right) \\\\
\frac{1}{y} y' &= \ln a \frac{d}{dx} \left( x \right) \\\\
\frac{1}{y} y' &= \ln a \\\\
y' &= y \ln a = a^x \ln a
\end{align} \]
Kaya
Next, let's look at the differentiation formulas for inverse trigonometric functions.
The derivatives of inverse trigonometric functions
\[ \begin{align}
&\left( \sin ^{-1} x \right) ' = \frac{1}{\sqrt{1-x^2}} \ \ ( -1 \lt x \lt 1 ) \\\\
&\left( \cos ^{-1} x \right) ' = - \frac{1}{\sqrt{1-x^2}} \ \ ( -1 \lt x \lt 1 ) \\\\
&\left( \tan ^{-1} x \right) ' = \frac{1}{1 + x^2} \ \ ( - \infty \lt x \lt \infty )
\end{align} \]
Kaya
Let’s start by proving the derivative of \( \sin ^{-1} x \).
Let \( y = \sin ^{-1} x \). Then \( x = \sin y \), and by the formula for the derivative of an inverse function,
\[ \begin{align}
\frac{dy}{dx} = \cfrac{1}{\cfrac{dx}{dy}}
= \frac{1}{\cos y}
\end{align} \]
Since, by the definition of the inverse sine function, \( - \pi / 2 \leq y \leq \pi / 2 \), we have \( \cos y \geq 0 \).
Therefore,
\[ \begin{align}
\frac{dy}{dx} = \frac{1}{\cos y}
= \frac{1}{\sqrt{1-\sin ^2 y}}
= \frac{1}{\sqrt{1-x^2}}
\end{align} \]
Nayumi
Next, let’s consider \( \cos^{-1} x \).
Let \( y = \cos ^{-1} x \). Then \( x = \cos y \), and by the formula for the derivative of an inverse function,
\[ \begin{align}
\frac{dy}{dx} = \cfrac{1}{\cfrac{dx}{dy}}
= - \frac{1}{\sin y}
\end{align} \]
Since, by the definition of the inverse cosine function, \( 0 \leq y \leq \pi \), we have \( \sin y \geq 0 \).
Therefore,
\[ \begin{align}
\frac{dy}{dx} = - \frac{1}{\sin y}
= - \frac{1}{\sqrt{1-\cos ^2 y}}
= - \frac{1}{\sqrt{1-x^2}}
\end{align} \]
Kaya
Lastly, let’s prove the derivative of \( \tan ^{-1} x \).
Let \( y = \tan ^{-1} x \). Then \( x = \tan y \), and by the formula for the derivative of an inverse function,
\[ \begin{align}
\frac{dy}{dx} = \cfrac{1}{\cfrac{dx}{dy}}
= \cos ^2 y
= \frac{1}{1 + \tan ^2 y}
= \frac{1}{1 + x^2}
\end{align} \]
Kaya
Finally, let's briefly explain the \( n \)th order derivative function before wrapping up.
\( n \)th order derivative function
Nayumi
\( n \)th order derivative function?
Kaya
The \( n \)th order derivative function simply means the function differentiated \( n \) times. More
precisely, it is defined as follows.
\[ n \text{th order derivative function}\]
Define the \( \boldsymbol n \)th order derivative function \( f^{\left( n \right)} (x) \)
of the function \( y = f(x) \) with \( n \) as a natural number.
[1] \( f^{\left( 1 \right) } (x) = f'(x) \)
[2] \( f^{\left( n \right) } (x) = \left\{ f^{\left( n - 1 \right) } (x) \right\} ' \)
Other symbols representing the \( n \)th order derivative function are \( y^{\left( n \right)} \), \( \frac{d^n y}{dx^n} \) and \( \frac{d^n}{dx^n} f(x) \).
[1] \( f^{\left( 1 \right) } (x) = f'(x) \)
[2] \( f^{\left( n \right) } (x) = \left\{ f^{\left( n - 1 \right) } (x) \right\} ' \)
Other symbols representing the \( n \)th order derivative function are \( y^{\left( n \right)} \), \( \frac{d^n y}{dx^n} \) and \( \frac{d^n}{dx^n} f(x) \).
Nayumi
You write the number of times differentiated as a superscript to the right of \( f \), right?
Kaya
That's right. In addition, there is the following classification based on the number of times a function
can be differentiated and the continuity of its derivatives.
\[ \begin{align}
C^n \text{-function}
\end{align}\]
If the \( n \)th derivative \( f^{\left( n \right) } (x) \) of a function \( y = f(x) \) exists, then
\( f(x) \) is said to be \( \boldsymbol n \)-times differentiable.
Furthermore, if \( f^{\left( n \right) } (x) \) is continuous, \( f(x) \) is called an \( \boldsymbol n
\)-times
continuously differentiable function, or a \( \boldsymbol C^n \)-function.
In addition, if the \( m \)th derivative \( f^{\left( m \right) } (x) \) exists for every natural number
\( m \), then \( f(x) \) is called a \( \boldsymbol C^{\infty} \)-function.
Kaya
These terms might not be immediately necessary, but the second derivative will likely come up eventually
in explanations of numerical experiments.
Nayumi
I'll keep that in mind, at least roughly.
Kaya
Good. Let's wrap it up here for today.
References：
[1] James R. Newman, THE UNIVERSAL ENCYCLOPEDIA OF MATHEMATICS, George Allen & Unwin Ltd, 1964
[2] 石村園子, やさしく学べる微分積分, 共立出版, December 25, 1999
[3] 難波 誠, 数学シリーズ 微分積分学, 裳華房, January 20, 2009
Previous
Ep. 6
Derivative of a function of one variable
Derivative of a function of one variable
Next
Ep. 8
Indefinite integral
Indefinite integral