TABLE OF CONTENTS
・Derivative of a function of one variable
・Equivalent condition for differentiability
・Sum rule and constant factor rule
・Product rule and quotient rule
・Chain rule for composite functions
・Inverse function rule
Kaya
This time, let's go over the general theory of derivative of a function of one variable.
Derivative of a function of one variable
\[ \text{Derivative}\]
For a function of one variable \( y = f(x) \) whose domain is a real interval containing \( x = a \),
if
\[ \lim _{h \to 0} \frac{f(a + h) - f(a)}{h} \]
exists, then \( f(x) \) is differentiable at \( x = a \), and this limit is called the
derivative of \( f(x) \) at \( a \), and is denoted by \( f ' (a) \).
Derivative of \( f(x) \) at \( a \) is equal to the slope of the tangent line at \( x = a \) of \( f(x)
\).
A real interval is a range of real numbers expressed using inequalities.
\[ \text{Real interval}\]
A method for representing a range of real numbers. Using an inequality involving a variable \( x \) and
constants \( a \) and \( b \), it can be classified as follows.
\( [a,b] \) ： \( a \leqq x \leqq b \)
\( (a,b] \) ： \( a \lt x \leqq b \)
\( [a,b) \) ： \( a \leqq x \lt b \)
\( (a,b) \) ： \( a \lt x \lt b \)
\( [a,b] \) ： \( a \leqq x \leqq b \)
\( (a,b] \) ： \( a \lt x \leqq b \)
\( [a,b) \) ： \( a \leqq x \lt b \)
\( (a,b) \) ： \( a \lt x \lt b \)
Nayumi
The derivative as the slope of the tangent line?
Kaya
It might be better to think about this while looking at the graph.
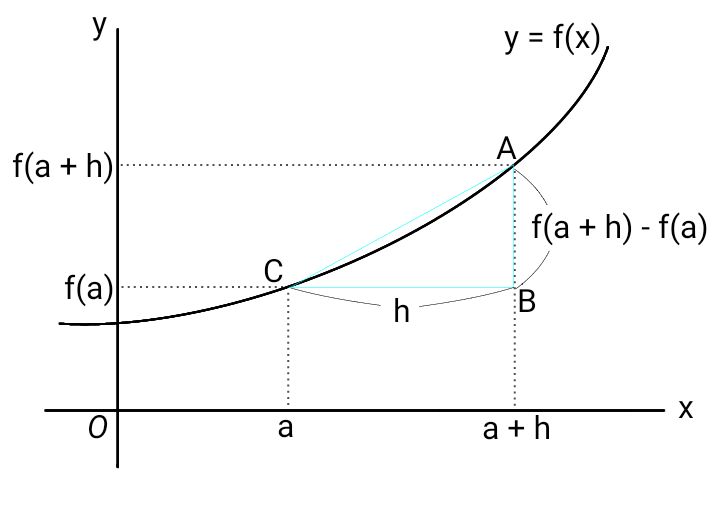
From the diagram, the expression \[ \frac{f(a + h) - f(a)}{h} \] that appears in the definition of the
derivative represents the slope of \( \rm AC \).
As \( h \) approaches zero, the light blue triangle \( \rm ABC \) becomes extremely small, keeping the point
\( \rm C \) fixed.
At this point, the slope of \( \rm AC \) becomes equal to the slope of the tangent line to \( f(x) \) at \(
x = a \), which is known as the derivative.
Nayumi
I see, so this is how you find the slope of a tangent line.
Kaya
While there are other ways to find the slope of a tangent for certain functions, the derivative is
probably the most general mathematical way to express it.
The definition of the derivative is the limit as \( x \) approaches a certain value \( a \), so we need to
specify \( a \) each time.
However, to make general discussions easier, we consider the following function.
\[ \text{Derivative function}\]
If a function \( y = f (x) \) is differentiable at every points \( x \) in a real interval, the
function that corresponds the derivative \( f ' (x) \) to \( x \) is called the derivative
function of \( y = f (x) \), and is expressed as \( y' \), \( f '(x) \), \( \frac{dy}{dx} \), \(
\frac{df}{dx} \), \( \frac{d}{dx} f (x) \), and so on.
There are various notations for derivatives, and it's fine to use whichever is most convenient depending on
the context.
Also, finding the derivative \( y = f'(x) \) from \( y = f(x) \) is referred to as 'differentiating' the
function.
Nayumi
So when you say 'differentiate,' it just means finding the derivative, right?
Kaya
That's right. Next, let's take a closer look at the condition of differentiability.
Equivalent condition for differentiability
\[ \begin{align}
\text{Equivalent condition for differentiability}
\end{align}\]
A necessary and sufficient condition for \( y = f(x) \) to be differentiable at \( x=a \) is that there
exists some \( \delta \gt 0 \) such that, on the real interval
\( (a - \delta , a + \delta) \), \( f(x) \) can be written in the form
\[ \begin{align}
f(x) = f(a) + (x-a) f'(a) + (x-a) B(x),
\end{align}\]
where \( B(x) \) is a function defined on \( (a - \delta , a + \delta) \) that is continuous at \( x=a
\) and satisfies \( B(a) = 0 \).
We now prove the equivalent condition for differentiability.
First, assume that \( f(x) \) is differentiable at \( x=a \). Define \( B(x) \) by
\[ B(x) =
\begin{cases}
\displaystyle \frac{f(x) - f(a)}{x-a} - f'(a) & (x \neq a) \\[1em]
\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 0 & (x = a)
\end{cases} \]
Then,
\[ \begin{align}
\lim _{x \to a} B(x) &= \lim _{x \to a} \left\{ \frac{f(x) - f(a)}{x-a} - f'(a) \right\} \\\\
&= f'(a) - f'(a) \\\\
&= 0 = B(a)
\end{align}\]
so \( B(x) \) is continuous at \( x = a \). Moreover, on the interval \( (a - \delta , a + \delta) \), we
have
\[ \begin{align}
f(x) = f(a) + (x-a) f'(a) + (x-a) B(x)
\end{align}\]
Conversely, suppose that on the interval \( (a - \delta , a + \delta) \), the function \( f(x) \) can be written in the form \[ \begin{align} f(x) = f(a) + (x-a) A + (x-a) B(x) \end{align}\] where \( A \) is a constant. For \( x \neq a \), dividing both sides by \( x - a \) gives \[ \begin{align} \frac{f(x) - f(a)}{x-a} = A + B(x) \end{align}\] Taking the limit as \( x \to a \), and using the fact that \( B(x) \) is continuous at \( x = a \) with \( B(a) = 0 \), we obtain \[ \begin{align} \lim _{x \to a} \frac{f(x) - f(a)}{x-a} = A = f'(a) \end{align}\] Thus, \( f(x) \) is differentiable at \( x = a \).
Conversely, suppose that on the interval \( (a - \delta , a + \delta) \), the function \( f(x) \) can be written in the form \[ \begin{align} f(x) = f(a) + (x-a) A + (x-a) B(x) \end{align}\] where \( A \) is a constant. For \( x \neq a \), dividing both sides by \( x - a \) gives \[ \begin{align} \frac{f(x) - f(a)}{x-a} = A + B(x) \end{align}\] Taking the limit as \( x \to a \), and using the fact that \( B(x) \) is continuous at \( x = a \) with \( B(a) = 0 \), we obtain \[ \begin{align} \lim _{x \to a} \frac{f(x) - f(a)}{x-a} = A = f'(a) \end{align}\] Thus, \( f(x) \) is differentiable at \( x = a \).
Kaya
We’ll use this equivalence later, so keep it in the back of your mind.
Nayumi
Hmm, I see. Got it.
Kaya
Alright then, next let’s introduce some important differentiation formulas.
Sum rule and constant factor rule
Nayumi
Are there a lot of differentiation formulas?
Kaya
There are quite a few, but here, we'll focus on the most common ones.
\[\text{Sum rule and constant factor rule} \]
If the functions \( f(x) \) and \( g(x) \) are differentiable on the real interval \( I \), then, with
\( c \) as a real constant, \( cf(x) \) and \( f(x) \pm g(x) \) are also differentiable on \( I \), and
the following equations hold.
\[ \left\{ cf(x) \right\} ' = c f'(x) \]
\[ \left\{ f(x) \pm g(x) \right\} ' = f'(x) \pm g'(x)\]
Kaya
First, the proof of the constant factor rule.
\[ \text{Proof of the constant factor rule}\]
\[ \begin{align}
\left\{ cf(x) \right\} ' &= \lim _{h \to 0} \frac{cf(x+h) - cf(x)}{h} \\\\
&= \lim _{h \to 0} \frac{c \left\{ f(x+h) - f(x) \right\} }{h} \\\\
&= c \lim _{h \to 0} \frac{f(x+h) - f(x)}{h} \\\\
&= c f'(x)
\end{align}\]
Nayumi
Next is the proof of the sum rules.
\[\text{Proof of the sum rule}\]
\[ \begin{align}
\left\{ f(x) \pm g(x) \right\} ' &= \lim _{h \to 0} \frac{\left\{ f(x+h) \pm g(x+h) \right\} - \left\{
f(x) \pm g(x) \right\}}{h} \\\\
&= \lim _{h \to 0} \frac{\left\{ f(x+h) - f(x) \right\} \pm \left\{ g(x+h) - g(x) \right\}}{h} \\\\
&= \lim _{h \to 0} \frac{f(x+h) - f(x)}{h} \pm \lim _{h \to 0} \frac{ g(x+h) - g(x)}{h} \\\\
&= f'(x) \pm g'(x)
\end{align}\]
Kaya
Keep in mind that the signs switch when subtracting. Next, we'll cover the product and quotient
differentiation formulas.
Product rule and quotient rule
\[\text{Product rule and quotient rule}\]
If the functions \( f(x) \) and \( g(x) \) are differentiable on the real interval \( I \), then \(
f(x)g(x) \) and \( \frac{f(x)}{g(x)} \) (where \( g(x) \neq 0 \)) are also differentiable on \( I \),
and the following equations hold:
\[ \left\{ f(x)g(x) \right\} ' = f'(x)g(x) + f(x)g'(x) \]
\[ \left\{ \frac{f(x)}{g(x)} \right\} ' = \frac{f'(x)g(x) - f(x)g'(x)}{\left\{ g(x) \right\} ^2 } \]
Nayumi
This is getting a bit tricky.
Kaya
It’s a bit more complex than before. Let’s start with the product rule.
\[ \text{Proof of the product rule}\]
\[ \begin{align}
\left\{ f(x)g(x) \right\} ' &= \lim _{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x)}{h} \\\\
&= \lim _{h \to 0} \frac{f(x+h)g(x+h) - f(x)g(x+h) + f(x)g(x+h) - f(x)g(x)}{h} \\\\
&= \lim _{h \to 0} \frac{\left\{ f(x+h)- f(x) \right\} g(x+h) + f(x) \left\{ g(x+h) - g(x) \right\}}{h}
\\\\
&= \lim _{h \to 0} \left\{ \frac{f(x+h)- f(x)}{h} g(x+h) + f(x) \frac{ g(x+h) - g(x) }{h} \right\} \\\\
&= f'(x)g(x) + f(x)g'(x)
\end{align}\]
The second line has \[ - f(x)g(x+h) + f(x)g(x+h) \] added to the numerator. This is effectively adding
zero, so it's perfectly valid to do this.
This adjustment allows us to rewrite the expression in the third and fourth lines in a form that matches the
definition of the derivative.
Kaya
Next, let's take a look at the quotient rule for differentiation.
\[ \text{Proof of the quotient rule}\]
\[ \begin{align}
\left\{ \frac{f(x)}{g(x)} \right\} ' &= \lim _{h \to 0} \frac{\frac{f(x+h)}{g(x+h)} -
\frac{f(x)}{g(x)}}{h} \\\\
&= \lim _{h \to 0} \frac{f(x+h)g(x) - f(x)g(x+h)}{hg(x+h)g(x)} \\\\
&= \lim _{h \to 0} \frac{1}{g(x+h)g(x)} \frac{f(x+h)g(x) - f(x)g(x) + f(x)g(x) - f(x)g(x+h)}{h} \\\\
&= \lim _{h \to 0} \frac{1}{g(x+h)g(x)} \frac{\left\{ f(x+h) - f(x) \right\} g(x) - f(x) \left\{ g(x+h)
- g(x) \right\} }{h} \\\\
&= \lim _{h \to 0} \frac{1}{g(x+h)g(x)} \left\{ \frac{f(x+h) - f(x)}{h} g(x) - f(x) \frac{g(x+h) -
g(x)}{h} \right\} \\\\
&= \frac{1}{g(x)g(x)} \left\{ f'(x)g(x) - f(x)g'(x) \right\} \\\\
&= \frac{f'(x)g(x) - f(x)g'(x)}{\left\{ g(x) \right\}^2}
\end{align}\]
In the third line, as before, the term \[ - f(x)g(x) + f(x)g(x) \], which sums to zero, is added to the
numerator to set up the definition of the derivative.
Kaya
Alright, let's go over the chain rule for composite functions.
Chain rule for composite functions
\[\text{Chain rule for composite functions}\]
Suppose that the function \( u = f(x) \) is differentiable on the real interval \( I \), the function
\( y = g(u) \) is differentiable on the real interval \( J \), and the image of \( u = f(x) \) is
included in \( J \).
In this case, the composite function \( y = g(f(x)) \) is differentiable on the real interval \( I \),
and the following equation holds.
\[ y' = g'(u)f'(x) \]
A function of the form \( y = g(f(x)) \) is called a composite function.
A composite function is only defined if the image of \( f \) is contained within the domain of \( g \).
Before proving the chain rule for composite functions, let's first establish the following preliminary
theorem.
If \( y = f(x) \) is differentiable at \( x = a \), then it is also continuous at \( x = a \).
Nayumi
It's been a while since we talked about continuity.
Kaya
That's right. Here's the proof.
To show that \( y = f(x) \) is continuous at \( x = a \), we need to prove
\[ \lim _{x \to a} f(x) = f(a) \]
Setting \( x = a + h \), we have \( h \to 0 \) as \( x \to a \), so it is sufficient to show
\[ \lim _{h \to 0} f(a+h) = f(a) \]
By the assumption that \( y = f(x) \) is differentiable at \( x = a \), we have
\[ \begin{align}
\lim _{h \to 0} \left\{ f(a+h) - f(a) \right\} &= \lim _{h \to 0} \frac{f(a+h) - f(a)}{h} \times h
\\\\
&= f'(a) \times 0 = 0
\end{align}\]
Therefore,
\[ \lim _{h \to 0} f(a+h) = f(a) \]
which completes the proof.
Nayumi
You've cleverly rewritten the variable to bring in the definition of the derivative.
Kaya
Exactly. Now, let's move on to proving the chain rule for composite functions.
\[ \text{Proof of the chain rule for composite functions}\]
By assumption, \( g(u) \) is differentiable, so
\[ g'(u) = \lim _{k \to 0} \frac{g(u+k) - g(u)}{k} \]
exists. Now, let
\[ k = f(x+h) - f(x).\]
Since \( f(x) \) is differentiable by assumption, it is also continuous, which means
\[ \lim _{h \to 0} f(x+h) = f(x) .\]
Thus,
\[ \lim _{h \to 0} k = \lim _{h \to 0} \left\{ f(x+h) - f(x) \right\} = 0.\]
Therefore,
\[ \begin{align}
y' &= \lim _{h \to 0} \frac{g(f(x+h))-g(f(x))}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(f(x)+k)-g(f(x))}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(u+k)-g(u)}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(u+k)-g(u)}{k} \times \frac{k}{h} \\\\
&= \lim _{h,k \to 0} \frac{g(u+k)-g(u)}{k} \times \frac{f(x+h) - f(x)}{h} \\\\
&= g'(u)f'(x)
\end{align}\]
Kaya
Alright then, let’s finish by working on the differentiation formula for inverse functions.
Inverse function rule
\[\text{Inverse function rule}\]
Let \( y = f(x) \) be a monotonic (increasing or decreasing) function on a real interval \( I \), and
assume that \( f \) is differentiable on \( I \).
Then the inverse function \( x = f^{-1}(y) \) is differentiable at those values of \( y \) that
correspond to points \( x \) where \( f'(x) \neq 0 \), and the following formula holds.
\[ x' = \frac{1}{y'} \]
Nayumi
So the derivative of the inverse function is just the reciprocal of the derivative of the original function, huh.
Kaya
Exactly. The proof goes as follows.
\[\text{Proof of the derivative formula for inverse functions}\]
Consider a point \( a \) in the real interval \( I \) such that \( f'(a) \neq 0 \).
Let \( b = f(a) \).
Since \( y = f(x) \) is differentiable at \( x = a \), there exists some \( \delta \gt 0 \) such that, on the interval \( (a - \delta, a + \delta) \), we can write
\[ \begin{align}
y - b = (x-a) f'(a) + (x-a) B(x)
\end{align}\]
where \( B(x) \) is a function defined on \( (a - \delta, a + \delta) \), continuous at \( x = a \), and satisfying \( B(a) = 0 \).
Noting that \( f'(a) \neq 0 \) and \( x = f^{-1}(y) \), we obtain
\[ \begin{align}
y - b &= \left( f^{-1} (y) - a \right) f'(a) + \left( f^{-1} (y) -a \right) B\left( f^{-1} (y)
\right) \\\\
f^{-1} (y) - a &= \frac{1}{f'(a)} \left( y-b \right) - \frac{1}{f'(a)} \cdot \left( f^{-1} (y) -a
\right) B\left( f^{-1} (y) \right) \\\\
&= \left( y-b \right) \cdot \frac{1}{f'(a)} + \left( y-b \right) \cdot \frac{\left( f^{-1} (y) -a
\right) B\left( f^{-1} (y) \right)}{f'(a)\left( b-y \right)} \\\\
&= \left( y-b \right) \cdot \frac{1}{f'(a)} + \left( y-b \right) \cdot \frac{-B\left( f^{-1} (y)
\right)}{f'(a) \left\{ f'(a) + B\left( f^{-1} (y) \right) \right\}}
\end{align}\]
Now define
\[ \begin{align}
C(y) = \frac{-B\left( f^{-1} (y) \right)}{f'(a) \left\{ f'(a) + B\left( f^{-1} (y) \right) \right\}}
\end{align}\]
This function satisfies \( C(b) = 0 \) and is continuous at \( y = b \).
Therefore, the inverse function \( x = f^{-1}(y) \) is differentiable at \( y = b \), and
\[ x' = \frac{1}{y'} \]
holds.
You can also “explain” the derivative formula for inverse functions in the following way.
\[\text{Explanation of the derivative formula for inverse functions}\]
On a real interval \( I \), differentiate both sides of the equation
\( x = f^{-1}(y) \) with respect to \( x \):
\[ \begin{align}
\frac{d}{dx} (x) &= \frac{d}{dx} f^{-1} (y)
\end{align}\]
By the chain rule for composite functions,
\[ \begin{align}
1 &= \frac{df^{-1} (y)}{dy} \cdot \frac{dy}{dx}
\end{align}\]
Thus, if \( dy/dx \neq 0 \), then
\[ \begin{align}
\frac{df^{-1} (y)}{dy} &= \cfrac{1}{\cfrac{dy}{dx}} \\\\
\frac{dx}{dy} &= \cfrac{1}{\cfrac{dy}{dx}} \\\\
x' &= \frac{1}{y'}
\end{align}\]
This completes the explanation.
In the explanation above, the use of the chain rule assumes differentiability of
\( x = f^{-1}(y) \) without proving it, so this does not constitute a rigorous proof.
However, it is a convenient way to recall the derivative formula for inverse functions.
Nayumi
So, are we done with the differentiation formulas now?
Kaya
Yes. Next time, we'll cover the differentiation of specific functions like trigonometric functions.
References：
[1] James R. Newman, THE UNIVERSAL ENCYCLOPEDIA OF MATHEMATICS, George Allen & Unwin Ltd, 1964
[2] 石村園子, やさしく学べる微分積分, 共立出版, December 25, 1999
[3] 難波 誠, 数学シリーズ 微分積分学, 裳華房, January 20, 2009
Previous
Ep. 5
Exponential and logarithmic functions
Exponential and logarithmic functions
Next
Ep. 7
Derivatives of
various functions
Derivatives of
various functions