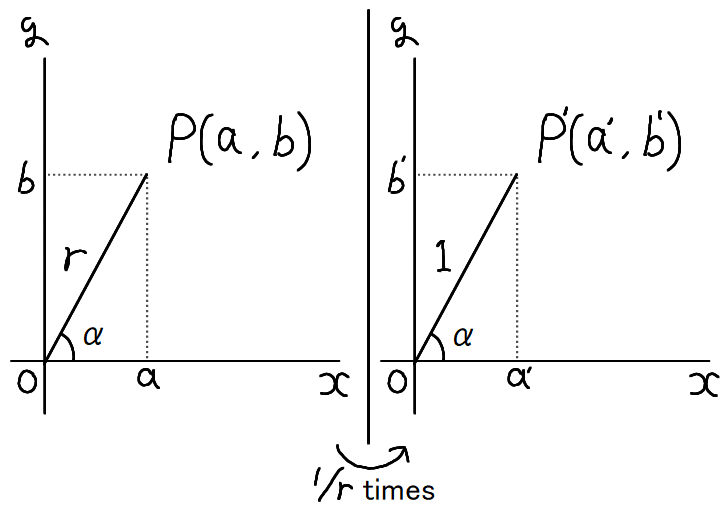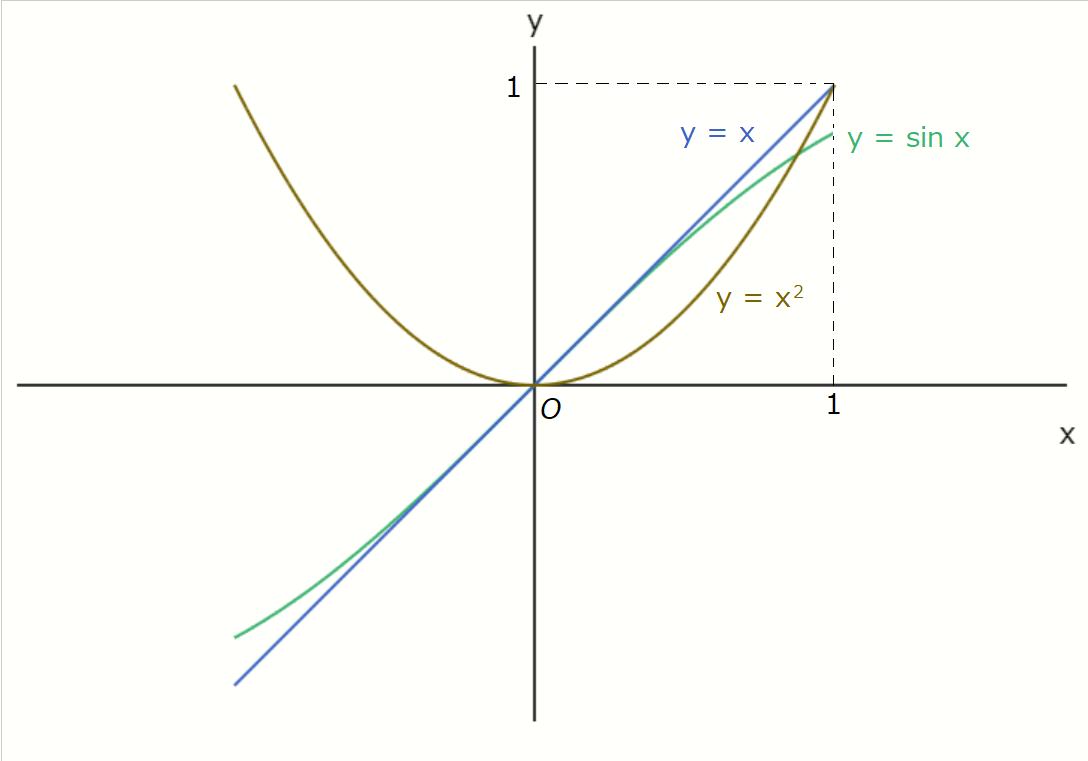
TABLE OF CONTENTS
・The definition of an angle
・Trigonometric function
・Sum and difference formulas
・Composition of trigonometric functions
・Sum to product and product to sum formula
・The limit formula of the sinc function
・Note: inverse trigonometric functions
Kaya
This time, we'll be exploring trigonometric functions. Let's start with the definition of an angle.
The definition of an angle
Nayumi
An angle is just an angle, right? Like \( 180^{\circ} \) or something.
Kaya
In everyday life, angles are usually expressed in degrees (\( ^{\circ} \)), but in mathematics, we use a
method called radians to represent angles.
\[ \text{Radian measure} \]
In a circle with a radius of 1, the central angle corresponding to an arc length of \(
\theta \) is called radian.
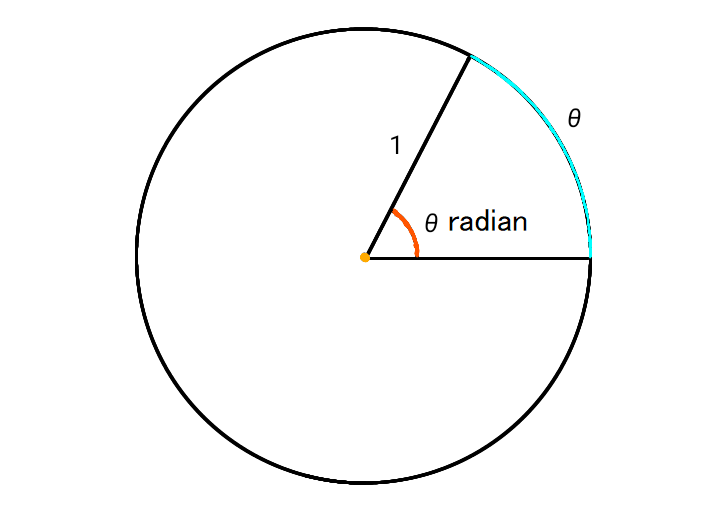
The yellow area in the diagram above represents the center of the circle. Just outside that, the orange
area shows the angle, and the outermost light blue arc represents the arc length.
Both the angle and the arc length are labeled as \( \theta \). The unit of the angle is radians, but the
unit is often omitted in practice.
There’s a fundamental relationship between radians and degrees (\( ^{\circ} \)):
\[ \pi \text{ radians} = 180^{\circ} \]
Here, \( \pi \) is the mathematical constant pi, representing the ratio of a circle's circumference
to its diameter.
Since the circumference of a circle is given by:
\[ \text{Circumference} = \text{Diameter} \times \pi, \]
a circle with radius 1 (which means the diameter is 2) has a circumference of \( 2\pi \). The angle that
spans the entire circle is \( 360^{\circ} \), so:
\[ 2\pi \text{ radians} = 360^{\circ} \]
Dividing both sides by 2 gives us the key conversion formula:
\[ \pi \text{ radians} = 180^{\circ}\]
This formula is used to convert between degrees and radians.
Nayumi
In the radian system, the arc length and the angle are directly related, aren't they?
Kaya
Exactly. Now, let’s define a general angle and extend the concept of angle to cover all real numbers.
\[ \text{General angle} \]
First, consider a circle with radius 1 centered at the origin \( O \) in the Cartesian plane.
This circle is called the unit circle.
Let point \( A(1,0) \) be the starting point, and suppose that point \( P \) moves along the
circumference of the unit circle.
The angle \( \theta \) is determined as follows based on the movement of point \( P \):
[1] If point \( P \) moves counterclockwise along the unit circle, define \( \theta = \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \). If point \( P \) moves counterclockwise by \( n \) or more full circles, then define \( \theta = \angle POA + 2n \pi \), where \( n \) is any natural number.
[2] If point \( P \) moves clockwise along the unit circle, define \( \theta = - \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \). If point \( P \) moves clockwise by \( n \) or more full circles, then define \( \theta = - \angle POA - 2n \pi \), where \( n \) is any natural number.
[1] If point \( P \) moves counterclockwise along the unit circle, define \( \theta = \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \). If point \( P \) moves counterclockwise by \( n \) or more full circles, then define \( \theta = \angle POA + 2n \pi \), where \( n \) is any natural number.
[2] If point \( P \) moves clockwise along the unit circle, define \( \theta = - \angle POA \ \ \left( 0 \leq \angle POA \lt 2 \pi \right) \). If point \( P \) moves clockwise by \( n \) or more full circles, then define \( \theta = - \angle POA - 2n \pi \), where \( n \) is any natural number.
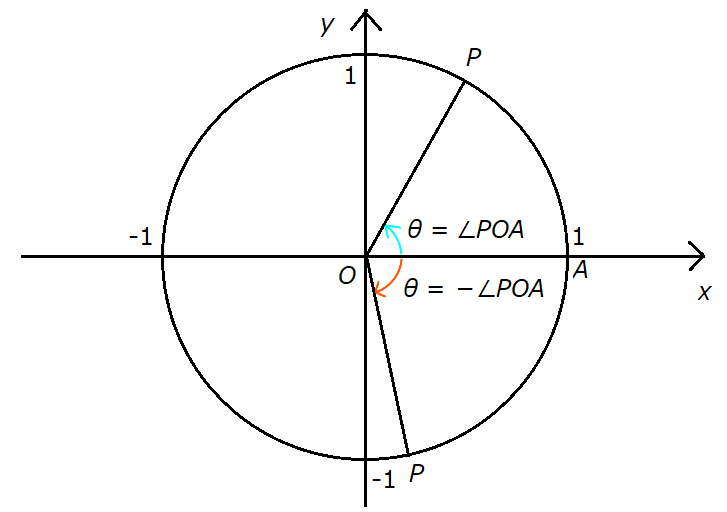
In the diagram above, clockwise rotation is indicated by the orange arrow, and counterclockwise rotation is
shown with the light blue arrow.
The angle \( \angle POA \) is read as “angle POA,” which refers to the angle formed by the line
segments \( OP \) and \( OA \).
A line segment is a straight line with two endpoints.
There are two regions associated with \( \angle POA \):
- the interior region enclosed by \( OP \) and \( OA \),
- and the exterior region on the opposite side.
When \( 0 \leq \theta \leq \pi \), the interior region is used to represent the general angle. When \( \pi \lt \theta \lt 2\pi \), the exterior region is used instead. The above diagram shows the case where the interior region is used. For the case where the exterior region is used, it would look like the diagram shown next.
- the interior region enclosed by \( OP \) and \( OA \),
- and the exterior region on the opposite side.
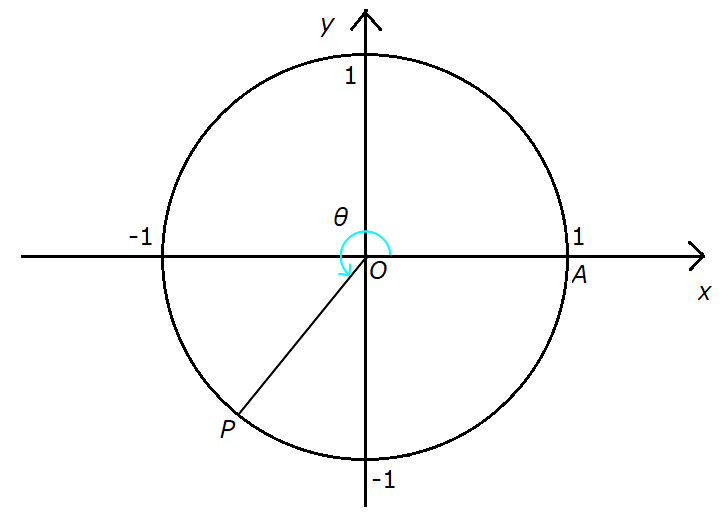
When \( 0 \leq \theta \leq \pi \), the interior region is used to represent the general angle. When \( \pi \lt \theta \lt 2\pi \), the exterior region is used instead. The above diagram shows the case where the interior region is used. For the case where the exterior region is used, it would look like the diagram shown next.
Nayumi
Point \( P \) goes around and around, and that’s how we get a general angle, right?
Kaya
That's right. Now, let's finally move on to trigonometric functions.
Trigonometric function
Nayumi
Since they're called trigonometric functions, I guess triangles have something to do with them,
right?
Kaya
Exactly. Here's how they're defined.
\[ \text{Trigonometric function}\]
On the unit circle, take a point \( P (x,y) \) and represent the general angle as \( \theta \).
In this case, the following three functions of \( \theta \) are called trigonometric functions.
\[ \sin \theta = y\]
\[ \cos \theta = x\]
\[ \tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{y}{x} \ (x \neq 0) \]
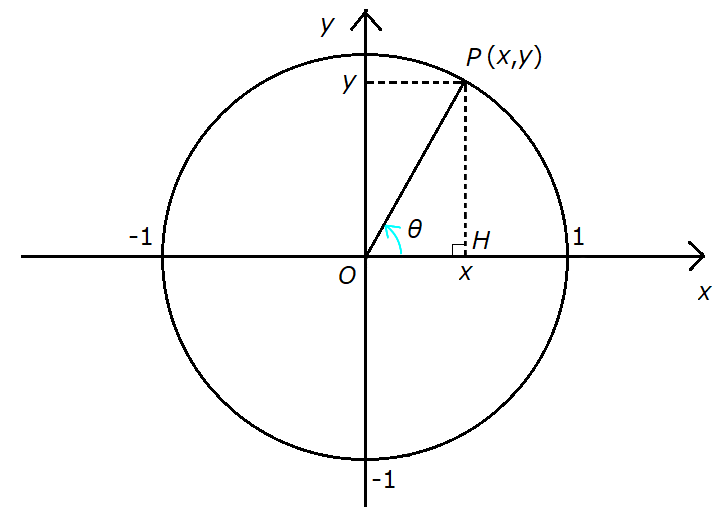
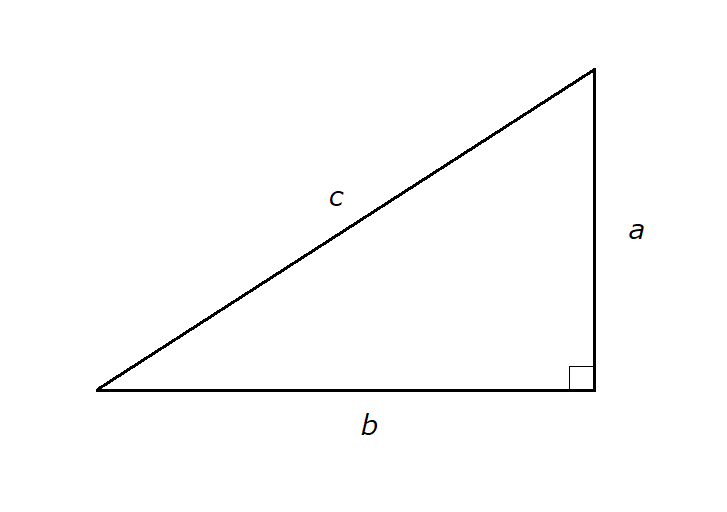
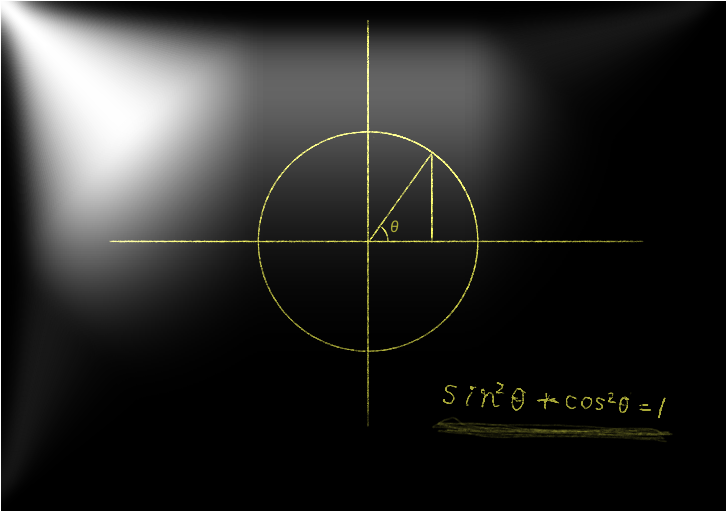
Since \( \triangle POH \) is a right triangle, we can apply the Pythagorean theorem:
\[ \text{Pythagorean theorem}\]
In a right triangle, let \( c \) be the length of the hypotenuse and \( a \), \( b \) be the lengths of
the other two sides.
Then, the following equation holds:
\[ c^2 = a^2 + b^2 \]
Since the right triangle \( \triangle POH \) has a hypotenuse of length 1—equal to the radius of the unit
circle—and the other two sides have lengths \( \sin \theta \) and \( \cos \theta \), applying the
Pythagorean theorem gives us the following equation:
\[ \sin ^2 \theta + \cos ^2 \theta = 1 \]
※In the above formula, we use the following notation.
\[ \begin{align}
\sin ^2 \theta &= \left( \sin \theta \right) ^2 \\\\
&= \left( \sin \theta \right) \times \left( \sin \theta \right) \\\\
\cos ^2 \theta &= \left( \cos \theta \right) ^2 \\\\
&= \left( \cos \theta \right) \times \left( \cos \theta \right)
\end{align}\]
Furthermore, by dividing both sides of this equation by \( \cos ^2 \theta \), we can derive the following
formula as well.
\[ \tan ^2 \theta + 1 = \frac{1}{\cos ^2 \theta} \]
※Here, we use the following notation.
\[ \begin{align}
\tan ^2 \theta &= \left( \tan \theta \right) ^2 \\\\
&= \left( \tan \theta \right) \times \left( \tan \theta \right)
\end{align}\]
Also, the general angle \( -\theta \) is the reflection of \( \theta \) across the \( x \)-axis, so \( \sin
\theta = y \) changes sign from positive to negative. On the other hand, \( \cos \theta = x \) remains
unchanged. This can be illustrated as shown below.
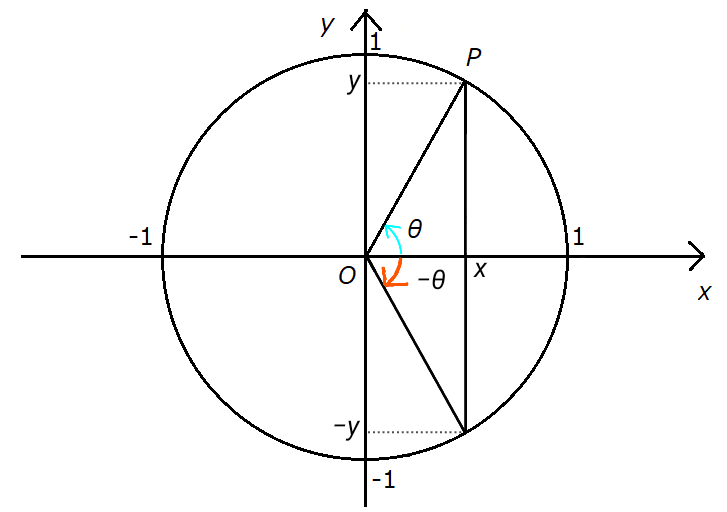
Based on this property, the following identity holds.
\[ \sin (- \theta ) = - \sin \theta \]
\[ \cos (- \theta ) = \cos \theta \]
\[ \tan (- \theta ) = \frac{\sin (- \theta) }{\cos (- \theta)} = \frac{- \sin \theta }{\cos \theta} = -
\tan \theta \]
Nayumi
What are trig function graphs like?
Kaya
Alright. Let's start by looking at the graphs of \( \sin \theta \) and \( \cos \theta \).
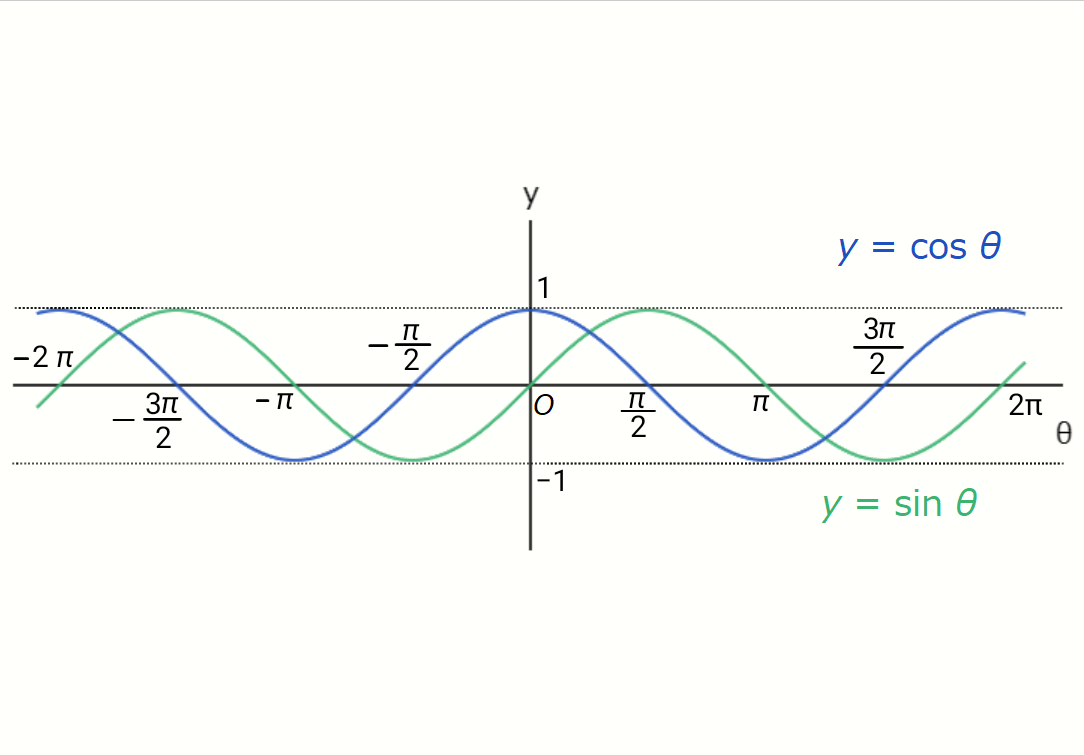
The graphs of \( y = \sin \theta \) and \( y = \cos \theta \) are called the sine wave and cosine
wave, respectively. Both of these functions are periodic functions with a period of \(
2\pi \). This is because, when a point \( P \) completes one revolution around the unit circle and returns
to its original position, the general angle \( \theta \) increases by \( 2\pi \).
Also, the maximum value of both functions is \( 1 \), and the minimum value is \( -1 \). This is because \( \sin \theta \) and \( \cos \theta \) correspond to the coordinates of a point \( P(x, y) \) on the unit circle, which has a radius of 1.
Moreover, as you can see from the graphs, the shapes of \( y = \sin \theta \) and \( y = \cos \theta \) are exactly the same—they are just horizontally shifted. This relationship can be expressed with the following equation:
Also, the maximum value of both functions is \( 1 \), and the minimum value is \( -1 \). This is because \( \sin \theta \) and \( \cos \theta \) correspond to the coordinates of a point \( P(x, y) \) on the unit circle, which has a radius of 1.
Moreover, as you can see from the graphs, the shapes of \( y = \sin \theta \) and \( y = \cos \theta \) are exactly the same—they are just horizontally shifted. This relationship can be expressed with the following equation:
\[ \sin \theta = \cos \left( \theta - \frac{\pi}{2} \right) \]
\[ \cos \theta = \sin \left( \theta + \frac{\pi}{2} \right) \]
\[ - \sin \theta = \cos \left( \theta + \frac{\pi}{2} \right) \]
\[ - \cos \theta = \sin \left( \theta - \frac{\pi}{2} \right) \]
Kaya
There are other things we can observe from these graphs, but let's leave \( \sin \) and \( \cos \) for
now and move on to the graph of \( \tan \).
Nayumi
What does the graph of \( \tan \) look like?
Kaya
This is it.
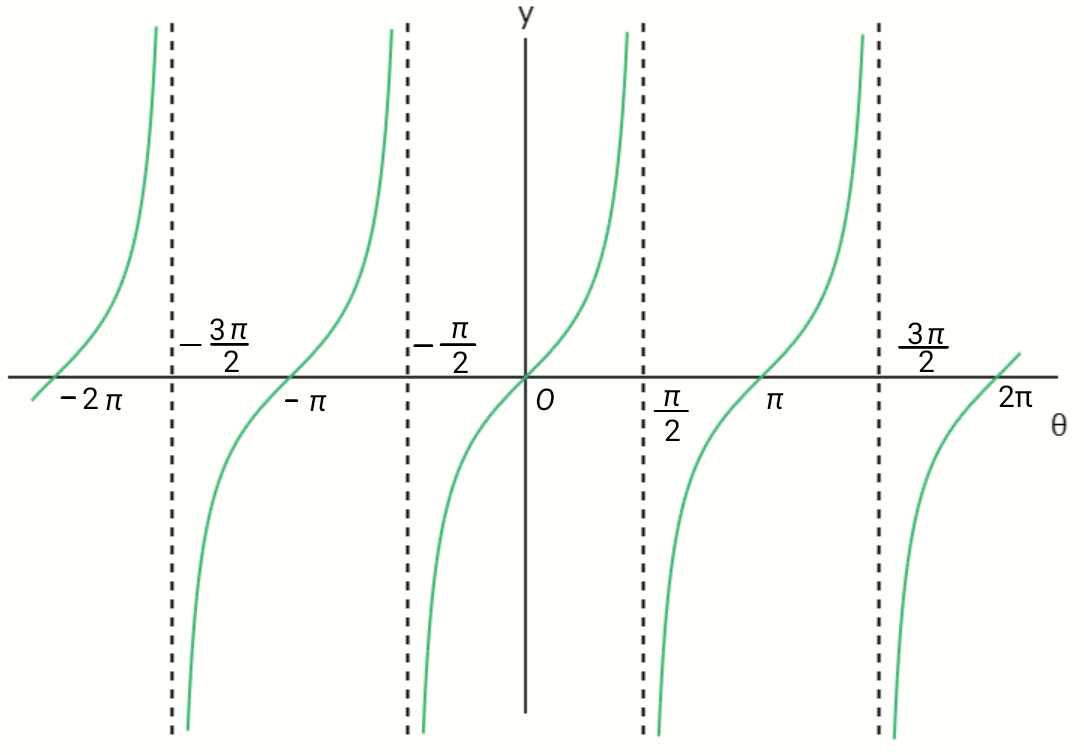
The function \( y = \tan \theta \) is a periodic function with a period of \( \pi \). Additionally, the
vertical asymptotes occur at \( x = \pm \frac{2n + 1}{2} \pi \ \ (n = 0,1,2, \ldots) \), and \( \tan \theta
\) is undefined at these values of \( x \).
Nayumi
It’s starting to look like a frame-by-frame film.
Kaya
Since the asymptotes are vertical lines. Let’s stop here with the trigonometric function graphs and move
on to explaining the sum and difference formulas.
Sum and difference formulas
\[ \text{Sum and difference formulas} \]
Let \( \alpha \) and \( \beta \) be general angles. Then, the following identities hold.
\[ \sin ( \alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \]
\[ \sin ( \alpha - \beta ) = \sin \alpha \cos \beta - \cos \alpha \sin \beta \]
\[ \cos ( \alpha + \beta ) = \cos \alpha \cos \beta - \sin \alpha \sin \beta \]
\[ \cos ( \alpha - \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \]
\[ \tan ( \alpha + \beta ) = \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta} \]
\[ \tan ( \alpha - \beta ) = \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta} \]
Nayumi
We’re diving into a formula fest now.
Kaya
The proof’s a little tricky, but it’s such a handy theorem, so let’s go over it.
First, let’s take two points on the unit circle: \( P (\cos \beta , \sin \beta) \) and \( Q (\cos \alpha ,
\sin \alpha ) \).
Here, let \( \angle POA = \beta \) and \( \angle QOA = \alpha \).
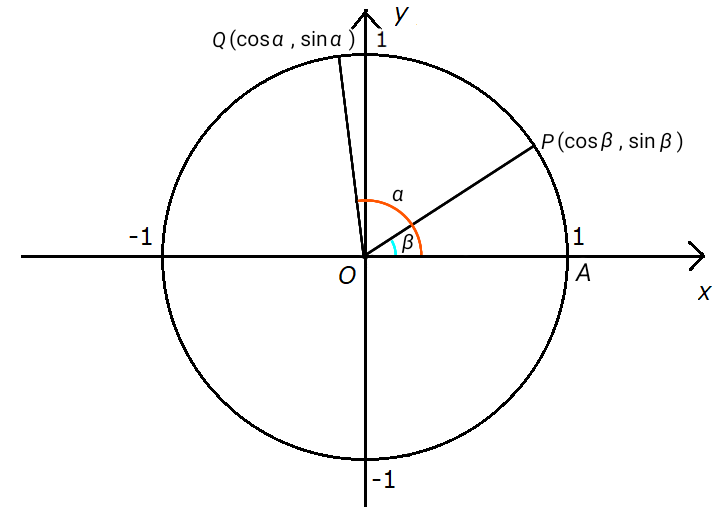
Next, consider triangle \( OPQ \), and draw a perpendicular line \( QH \) from point \( Q \) to the side \(
OP \).
Here, since \( \angle QOP = \alpha - \beta \), if we treat the line \( OP \) as the \( x \)-axis, we can see
that:
\[ QH = \sin(\alpha - \beta) \]
\[ OH = \cos(\alpha - \beta) \]
It might be easier to understand if you tilt your head to the left so that line \( OP \) appears horizontal.
Also, since
\[
\begin{align}
HP &= OP - OH \\\\
&= 1 - \cos (\alpha - \beta)
\end{align}
\]
holds, we can apply the Pythagorean theorem to triangle \( QHP \) to obtain the following equation.
\[ \begin{align}
PQ^2 &= QH^2 + HP^2 \\\\
&= \sin ^2 (\alpha - \beta ) + (1 - \cos (\alpha - \beta) )^2 \\\\
&= \sin ^2 (\alpha - \beta ) + 1 - 2 \cos (\alpha - \beta) + \cos ^2 (\alpha - \beta) \\\\
&= \left\{ \sin ^2 (\alpha - \beta ) + \cos ^2 (\alpha - \beta) \right\} + 1 - 2 \cos (\alpha - \beta)
\\\\
&= 2 - 2 \cos (\alpha - \beta)
\end{align} \]
The expression \( \sin^2(\alpha - \beta) + \cos^2(\alpha - \beta) \) equals 1, based on the identity we
derived earlier from the Pythagorean theorem:
\[ \sin^2 \theta + \cos^2 \theta = 1 \]
Also, the term \( (1 - \cos(\alpha - \beta))^2 \) is calculated using the following multiplication formula.
\[ \text{Multiplication formula}\]
\[ (a + b)^2 = a^2 + 2ab + b^2 \]
This formula can be derived by repeatedly applying the distributive property, as shown below.
\[ \begin{align}
(a + b)^2 &= (a + b) (a + b) \\\\
&= (a + b) a + (a + b) b \\\\
&= a^2 + ab + ab + b^2 \\\\
&= a^2 + 2ab + b^2
\end{align}\]
Nayumi
I’m barely keeping up.
Kaya
Alright. Now, let’s continue and find \( PQ^2 \) by forming another triangle.
Let the intersection of \( x = \cos \beta \) and \( y = \sin \alpha \) be denoted as \( R \).
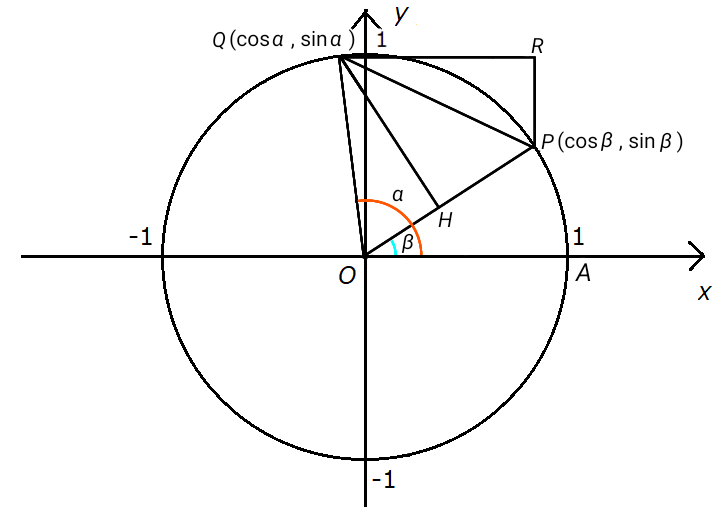
By applying the Pythagorean theorem to the triangle \( PQR \), we can find \( PQ^2 \) in a different form
from before.
\[ \begin{align}
PQ^2 &= RP^2 + QR^2 \\\\
&= \left( \sin \alpha - \sin \beta \right) ^2 + \left( \cos \alpha - \cos \beta \right) ^2 \\\\
&= \sin ^2 \alpha - 2 \sin \alpha \sin \beta + \sin ^2 \beta + \cos ^2 \alpha - 2 \cos \alpha \cos \beta
+ \cos ^2 \beta \\\\
&= 2 - 2 \left( \sin \alpha \sin \beta + \cos \alpha \cos \beta \right)
\end{align} \]
Thus, we have found \( PQ^2 \) in two different ways. Since the values obtained by both methods for \( PQ^2
\) are the same, these must be equal.
Therefore, the following equation holds, and one of the addition formulas is derived.
\[ \begin{align}
2 - 2 \cos (\alpha - \beta) &= 2 - 2 \left( \sin \alpha \sin \beta + \cos \alpha \cos \beta \right) \\\\
\cos (\alpha - \beta) &= \sin \alpha \sin \beta + \cos \alpha \cos \beta
\end{align}\]
Nayumi
I feel a sense of accomplishment. But we’ve only got one so far...
Kaya
Don’t worry, it’ll go faster from here, so you don’t have to be too concerned.
Nayumi
Really?
Kaya
Yeah. First, let’s substitute \( \beta = - \beta \) into the formula for \( \cos (\alpha - \beta) \) we
derived earlier and manipulate the equation.
\[ \begin{align}
\cos (\alpha - (- \beta ) ) &= \cos \alpha \cos ( - \beta ) + \sin \alpha \sin (- \beta ) \\\\
\cos (\alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta
\end{align} \]
Here, we used the following formulas.
\[ \sin (- \beta ) = - \sin \beta \]
\[ \cos (- \beta ) = \cos \beta \]
Nayumi
So, with that, we’ve got the addition formula for \( \cos (\alpha + \beta ) \), huh.
Kaya
Yep. Pretty fast, right? Next, let’s substitute \[ \beta = \beta + \frac{\pi}{2} \] into the formula for
\( \cos (\alpha + \beta ) \) we just derived and manipulate the equation.
\[ \begin{align}
\cos \left( \alpha + \left( \beta + \frac{\pi}{2} \right) \right) &= \cos \alpha \cos \left( \beta +
\frac{\pi}{2} \right) - \sin \alpha \sin \left( \beta + \frac{\pi}{2} \right) \\\\
\cos \left( ( \alpha + \beta ) + \frac{\pi}{2} \right) &= \cos \alpha (- \sin \beta ) - \sin \alpha \cos
\beta \\\\
- \sin ( \alpha + \beta ) &= - \cos \alpha \sin \beta - \sin \alpha \cos \beta \\\\
\sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta
\end{align} \]
Here, we used the following formulas.
\[ \sin \left( \theta + \frac{\pi}{2} \right) = \cos \theta \]
\[ \cos \left( \theta + \frac{\pi}{2} \right) = - \sin \theta \]
Kaya
With this, we’ve found the addition formula for \( \sin ( \alpha + \beta ) \). Now, let’s substitute \(
\beta = - \beta \) into it.
\[ \begin{align}
\sin (\alpha + (- \beta ) ) &= \sin \alpha \cos ( - \beta ) + \cos \alpha \sin (- \beta ) \\\\
\sin (\alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta
\end{align} \]
Nayumi
We’ve found the formula for \( \sin (\alpha - \beta ) \), right?
Kaya
Yeah. Now we’ve got the addition formulas for both \( \sin \) and \( \cos \).
Nayumi
The remaining one is for \( \tan \).
Kaya
The addition formula for \( \tan \) can be derived from the addition formulas for \( \sin \) and \( \cos
\). Let’s start with \( \tan (\alpha + \beta) \).
\[ \begin{align}
\tan (\alpha + \beta) &= \frac{\sin (\alpha + \beta)}{\cos (\alpha + \beta)} \\\\
&= \frac{\sin \alpha \cos \beta + \cos \alpha \sin \beta}{\cos \alpha \cos \beta - \sin \alpha \sin
\beta} \\\\
&= \frac{\tan \alpha + \tan \beta}{1 - \tan \alpha \tan \beta}
\end{align} \]
From the second line to the third line, we divided both the numerator and denominator by \( \cos \alpha \cos
\beta \).
Nayumi
I see, it works out pretty nicely.
Kaya
Yeah. And \( \tan (\alpha - \beta) \) can be obtained by substituting \( \beta = - \beta \) into the
formula for \( \tan (\alpha + \beta) \).
\[ \begin{align}
\tan (\alpha + (- \beta)) &= \frac{\tan \alpha + \tan (- \beta)}{1 - \tan \alpha \tan (- \beta) } \\\\
\tan (\alpha - \beta ) &= \frac{\tan \alpha - \tan \beta}{1 + \tan \alpha \tan \beta }
\end{align} \]
Here, we used the following formula.
\[ \tan ( - \beta ) = - \tan \beta \]
Kaya
With this, we’ve derived the addition formulas for \( \sin \), \( \cos \), and \( \tan \).
Nayumi
It was long, but once we got one, the rest just followed easily.
Kaya
Exactly. Now, let’s move on and introduce the trigonometric identities for the composition that can be
derived from the addition formulas.
Composition of trigonometric functions
\[ \text{Composition of trigonometric functions} \]
\[ a \sin \theta + b \cos \theta = \sqrt{a^2 + b^2} \sin \left( \theta + \alpha \right) \]
Here,
\[ \begin{align}
\cos \alpha &= \frac{a}{\sqrt{a^2 + b^2}} \\\\
\sin \alpha &= \frac{b}{\sqrt{a^2 + b^2}}
\end{align}\]
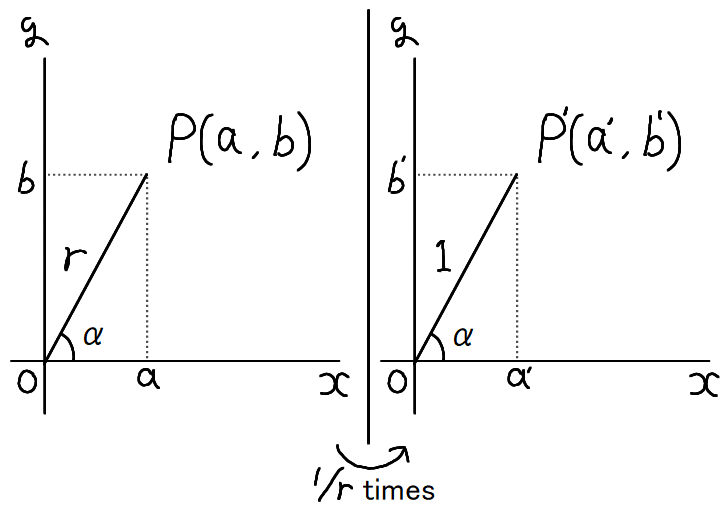
To derive this formula, we first place point \( a \) on the \( x \)-axis and point \( b \) on the \( y
\)-axis, as shown on the left side of the diagram.
Then, for the point \( P \left( a, b \right) \), by the Pythagorean theorem, we have
\[ \begin{align}
OP = r = \sqrt{a^2 + b^2}
\end{align}\]
Next, we scale the left side of the diagram by \( 1/r \) in both the \( x \)- and \( y \)-directions.
This is shown on the right side of the diagram, where we have
\[ \begin{align}
a' &= \frac{a}{r} = \cos \alpha \\\\
b' &= \frac{b}{r} = \sin \alpha
\end{align}\]
Thus, we can conclude that
\[ \begin{align}
a \sin \theta + b \cos \theta &= r \cos \alpha \sin \theta + r \sin \alpha \cos \theta \\\\
&= r \left( \cos \alpha \sin \theta + \sin \alpha \cos \theta \right) \\\\
&= r \sin \left( \theta + \alpha \right)
\end{align}\]
Therefore, we have proven the trigonometric identity for the composition.
Nayumi
So, the sine and cosine of the same angle can be combined into a single sine, huh?
Kaya
Exactly. Now, let’s move on and introduce the sum and product identities that can be derived from the
addition formulas.
Sum to product and product to sum formula
Nayumi
So, these can be derived from the addition formulas.
Kaya
Yep. First, let’s introduce the formula that transforms a product into a sum.
\[ \text{Product to sum formula} \]
\[ \begin{align}
\sin \alpha \cos \beta &= \frac{1}{2} \left\{ \sin (\alpha + \beta) + \sin (\alpha - \beta) \right\}
\\\\
\cos \alpha \sin \beta &= \frac{1}{2} \left\{ \sin (\alpha + \beta) - \sin (\alpha - \beta) \right\}
\\\\
\cos \alpha \cos \beta &= \frac{1}{2} \left\{ \cos (\alpha + \beta) + \cos (\alpha - \beta) \right\}
\\\\
\sin \alpha \sin \beta &= - \frac{1}{2} \left\{ \cos (\alpha + \beta) - \cos (\alpha - \beta) \right\}
\\\\
\end{align}\]
Nayumi
There are four types of combinations of \( \sin \) and \( \cos \), huh?
Kaya
Yep. Let’s derive them one by one, starting from the first equation.
By adding both sides of the following equations:
\[ \begin{align}
\sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\sin (\alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \\
\end{align}\]
we get
\[ \sin ( \alpha + \beta ) + \sin (\alpha - \beta ) = 2 \sin \alpha \cos \beta \]
Then, by dividing both sides by 2 and swapping the left and right sides, we obtain
\[ \sin \alpha \cos \beta = \frac{1}{2} \left\{ \sin (\alpha + \beta) + \sin (\alpha - \beta) \right\}
\]
Nayumi
It’s surprisingly simple.
Kaya
Well, yeah. For the second-to-last equation, we just subtract both sides like this.
By subtracting both sides of the following equations:
\[ \begin{align}
\sin ( \alpha + \beta ) &= \sin \alpha \cos \beta + \cos \alpha \sin \beta \\
\sin (\alpha - \beta ) &= \sin \alpha \cos \beta - \cos \alpha \sin \beta \\
\end{align}\]
we get
\[ \sin ( \alpha + \beta ) - \sin (\alpha - \beta ) = 2 \cos \alpha \sin \beta \]
Then, by dividing both sides by 2 and swapping the left and right sides, we obtain
\[ \cos \alpha \sin \beta = \frac{1}{2} \left\{ \sin (\alpha + \beta) - \sin (\alpha - \beta) \right\}
\]
Nayumi
Almost the same.
Kaya
For the third equation, we add both sides of the \( \cos \) addition formula.
By adding both sides of the following equations:
\[ \begin{align}
\cos ( \alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\
\cos (\alpha - \beta ) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{align}\]
we get
\[ \cos ( \alpha + \beta ) + \cos (\alpha - \beta ) = 2 \cos \alpha \cos \beta \]
Then, by dividing both sides by 2 and swapping the left and right sides, we obtain
\[ \cos \alpha \cos \beta = \frac{1}{2} \left\{ \cos (\alpha + \beta) + \cos (\alpha - \beta) \right\}
\]
Nayumi
It’s all about \( \cos \), huh?
Kaya
Yeah. For the last equation, we subtract both sides of the \( \cos \) addition formula.
By subtracting both sides of the following equations:
\[ \begin{align}
\cos ( \alpha + \beta ) &= \cos \alpha \cos \beta - \sin \alpha \sin \beta \\
\cos (\alpha - \beta ) &= \cos \alpha \cos \beta + \sin \alpha \sin \beta \\
\end{align}\]
we get
\[ \cos ( \alpha + \beta ) - \cos (\alpha - \beta ) = - 2 \sin \alpha \sin \beta \]
Then, by dividing both sides by －2 and swapping the left and right sides, we obtain
\[ \sin \alpha \sin \beta = - \frac{1}{2} \left\{ \cos (\alpha + \beta) - \cos (\alpha - \beta) \right\}
\]
Nayumi
Among the four formulas, this is the only one where the \( -\frac{1}{2} \) appears outside the curly
brackets on the right-hand side.
Kaya
Yeah. Now that we’ve derived all the formulas for converting a product into a sum, let’s move on to the
formulas for converting a sum into a product.
\[ \text{Sum to product formula} \]
\[ \begin{align}
\sin A + \sin B &= 2 \sin \frac{A+B}{2} \cos \frac{A-B}{2} \\\\
\sin A - \sin B &= 2 \cos \frac{A+B}{2} \sin \frac{A-B}{2} \\\\
\cos A + \cos B &= 2 \cos \frac{A+B}{2} \cos \frac{A-B}{2} \\\\
\cos A - \cos B &= - 2 \sin \frac{A+B}{2} \sin \frac{A-B}{2}
\end{align}\]
Nayumi
So, there are four types here as well.
Kaya
To derive the sum to product formulas, we can simply apply a variable substitution to the product to sum
formulas.
In the product to sum formulas,
let
\[ \alpha + \beta = A \]
\[ \alpha - \beta = B \]
If we add these two equations, we get
\[ \alpha = \frac{A+B}{2} \]
and if we subtract them, we get
\[ \beta = \frac{A-B}{2} \]
By substituting these into the product to sum formulas, we can derive the sum to product formulas.
Nayumi
Hmm, I got it right away.
Kaya
It looks complicated, but once you try it, it’s not so bad, right?
Nayumi
Yeah. Still, I wonder when I’ll actually use these formulas.
Kaya
You’ll use them eventually, so don’t worry about it.
Nayumi
It’s not like I’m worried or anything.
Kaya
Is that so? Well then, let’s wrap things up by explaining a famous limit formula involving the sinc
function.
The limit formula of the sinc function
Nayumi
What's the sinc function?
Kaya
The definition of the sinc function is this.
\[ {\rm {sinc}} \ x = \frac{\sin x}{x} \]
Nayumi
So it’s \( \sin x \) divided by \( x \).
Kaya
Exactly. And this is what the graph of the function looks like.
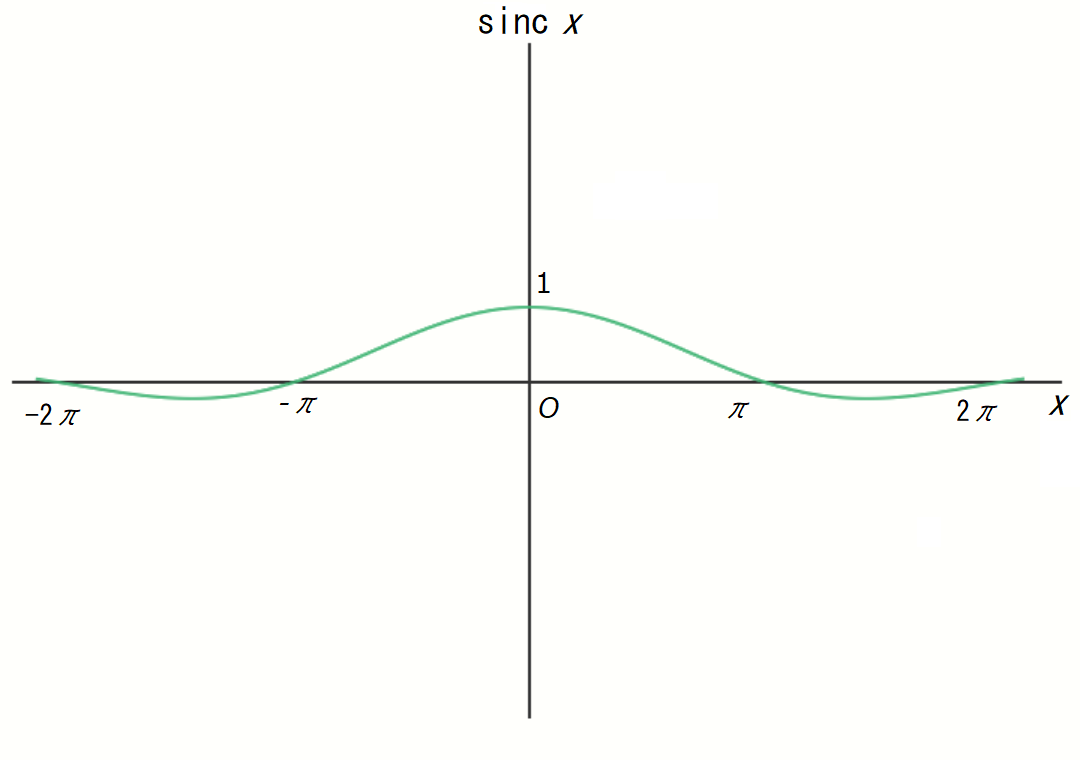
Nayumi
It looks like a mountain.
Kaya
Yeah, you could say that. And here’s the famous limit formula related to this function.
\[ \lim _{x \to 0} \frac{\sin x}{x} = 1 \]
The important point about this formula is that although both the numerator and denominator of the sinc
function become \(0\) at \(x = 0\), the sinc function still has a well-defined limit.
This isn't a simple matter of saying \(0 \div 0 = 1\); for example, if you replace the denominator of the
sinc function with \(x^2\) and plot the graph of the resulting function, you can see that it doesn't seem to
converge to \(1\) as \(x\) approaches \(0\).
However, it’s still true that for this function as well, both the numerator and denominator become \(0\) at
\(x = 0\).
\[ f(x) = \frac{\sin x}{x^2} \]
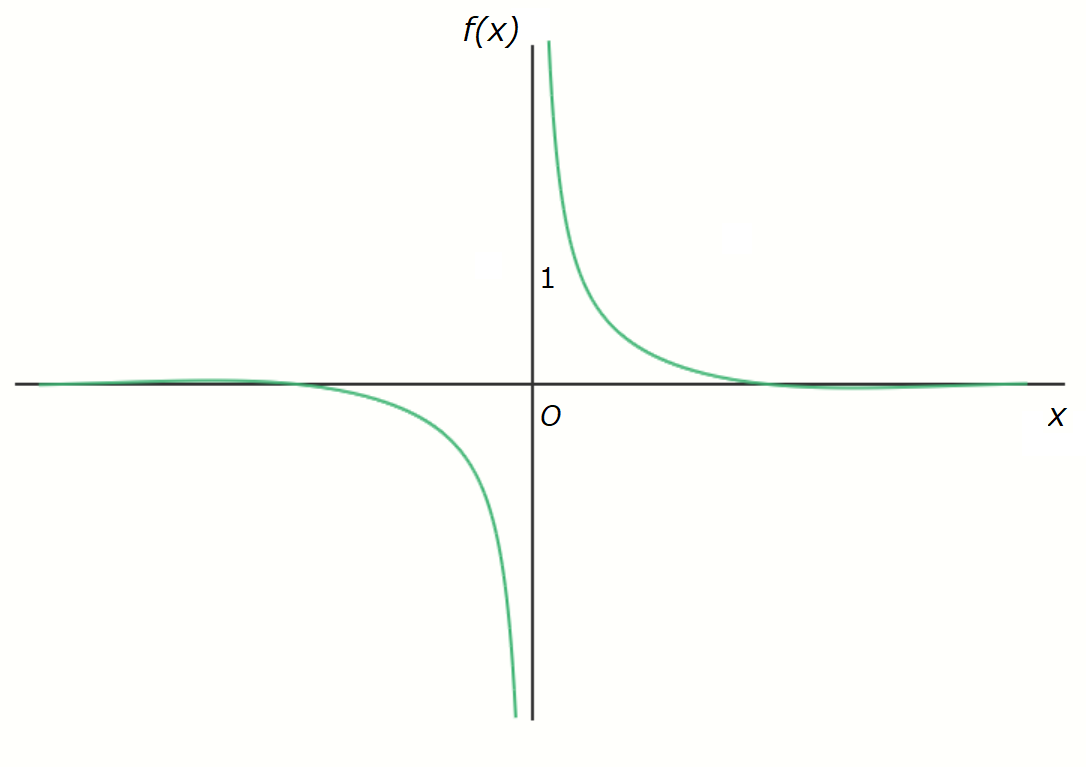
To put it simply, the difference is that near \(x = 0\), you can treat \(\sin x\) as essentially the same
as \(x\) without any problem.
For comparison, let's take a look at the graphs of \(\sin x\), \(x\), and \(x^2\) near \(x = 0\).
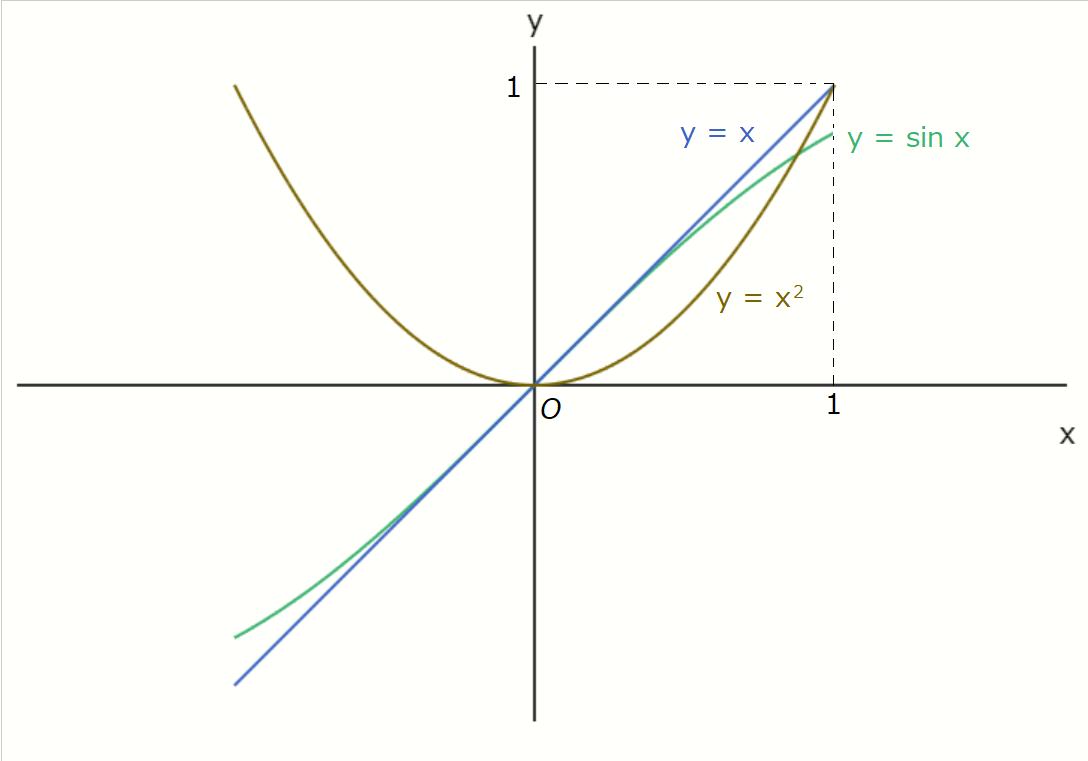
Nayumi
Hmm, it looks like after passing about \( x = \frac{1}{2} \), you can't really tell the difference
between \( \sin x \) and \( x \) anymore.
But when you're super close to \( x=0 \), all three graphs are at \( y=0 \) and completely
indistinguishable.
Kaya
Yeah, that's right. Then, shall we look at a version of this graph magnified \( 10 \) times?
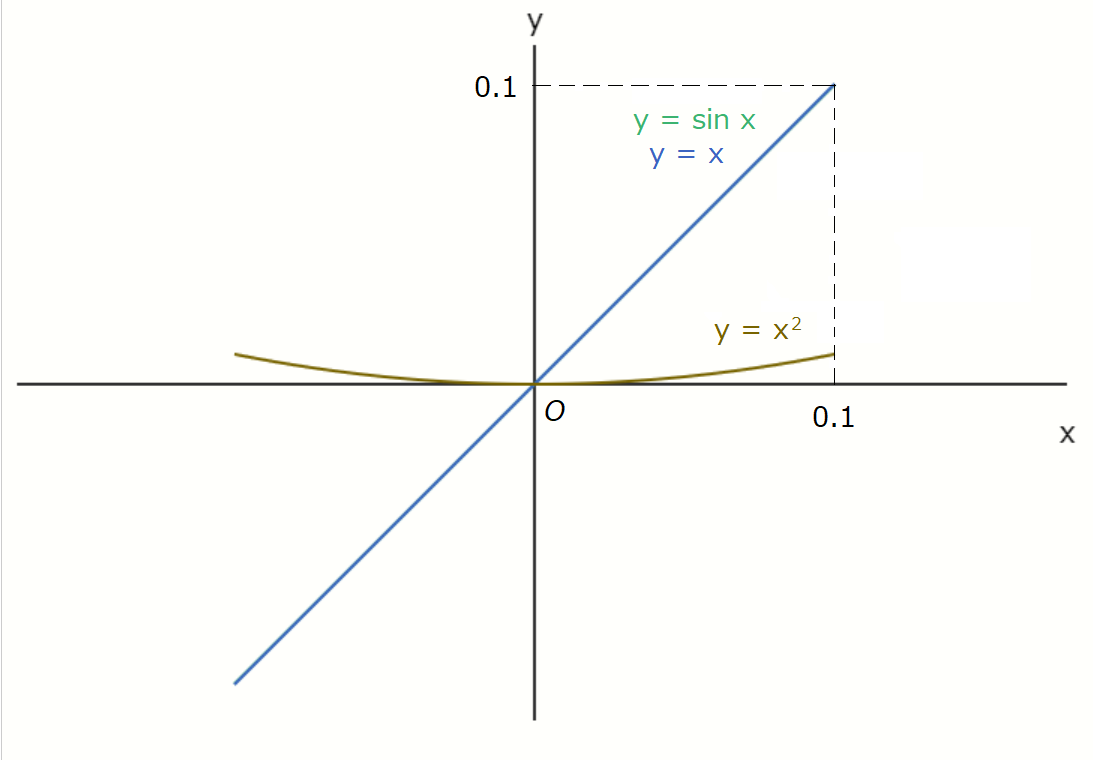
Nayumi
\( \sin x \) overlaps with \( x \) so perfectly that you can't even see it anymore... And \( x^2 \)
looks even flatter than before.
Kaya
Right. And if you keep zooming in forever, \( \sin x \) and \( x \) end up overlapping so closely that
you can't tell them apart anymore, whereas \( x^2 \) just flattens out completely.
That's the difference that creates the different behavior in the limits.
Nayumi
Dividing by zero is really tricky, huh.
Kaya
Yeah. Handling zero can be pretty tricky in mathematics.
Nayumi
Well, at least now I get the idea. Since we've covered the limit formula too, I guess that's it for
today?
Kaya
Yeah, let's wrap it up here for now.
Note: inverse trigonometric functions
\[ \begin{align}
\text{Inverse trigonometric functions}
\end{align}\]
When the domain of the function \( y = \sin x \) is restricted to \( \left[ -\pi/2, \pi/2 \right] \),
its inverse function is written as
\[ \begin{align}
y = \sin ^{-1} x \ \ \left( -1 \leq x \leq 1 \right)
\end{align}\]
Similarly, when the domain of \( y = \cos x \) is restricted to \( \left[ 0, \pi \right] \), its inverse
function is written as
\[ \begin{align}
y = \cos ^{-1} x \ \ \left( -1 \leq x \leq 1 \right)
\end{align}\]
Also, when the domain of \( y = \tan x \) is restricted to \( \left( -\pi/2, \pi/2 \right) \), its
inverse function is written as
\[ \begin{align}
y = \tan ^{-1} x \ \ \left( - \infty \leq x \leq \infty \right)
\end{align}\]
The functions \( \sin^{-1} x \), \( \cos^{-1} x \), and \( \tan^{-1} x \) are called inverse
trigonometric functions.
\( \sin ^{-1} x \) is read as “arc sine \( x \)” or “inverse sine \( x \).”
The same applies to \( \cos ^{-1} x \) and \( \tan ^{-1} x \).
Another notation for inverse trigonometric functions is:
\[ \begin{align}
\arcsin x,\ \arccos x,\ \arctan x
\end{align}\]
That is,
\[ \begin{align}
&\sin ^{-1} x = \arcsin x \\\\
&\cos ^{-1} x = \arccos x \\\\
&\tan ^{-1} x = \arctan x
\end{align}\]
These notations are often used interchangeably.
Nayumi
Even the same function can be written in various ways, huh.
Kaya
When reading a math book, we really need to make sure we understand what each symbol means.
References：
[1] James R. Newman, THE UNIVERSAL ENCYCLOPEDIA OF MATHEMATICS, George Allen & Unwin Ltd, 1964
[2] 石村園子, やさしく学べる微分積分, 共立出版, December 25, 1999
[3] 宮西正宜 23 others, 高等学校 数学Ⅱ 改訂版, 新興出版社啓林館, December 10, 2009
Previous
Ep. 3
Straight line and
conic section
Straight line and
conic section
Next
Ep. 5
Exponential and logarithmic functions
Exponential and logarithmic functions