TABLE OF CONTENTS
・Indefinite integral
・Indefinite integrals of various functions
Mathematics articles that help in reading this article
・Numerical Computation： Ep. 1, Ep. 2, Ep. 4, Ep. 5, Ep. 6, Ep. 7
・Numerical Computation： Ep. 1, Ep. 2, Ep. 4, Ep. 5, Ep. 6, Ep. 7
Kaya
This time, let's go over indefinite integrals.
Indefinite integral
Nayumi
Indefinite integrals?
Kaya
An indefinite integral is the reverse operation of differentiation.
Nayumi
The reverse of differentiation… you mean going back to what the function was before being
differentiated?
Kaya
Exactly. To explain that, let's first define what a antiderivative is.
\[ \text{Antiderivative}\]
Given a function \( f(x) \) , any function \( y = F (x) \) such that \( \frac{dy}{dx} = f (x) \) is an
antiderivative of \( f(x) \).
A function \( F(x) \) that satisfies \( F'(x) = f(x) \) is called a antiderivative.
The following theorem is also helpful for understanding indefinite integrals.
\[ \text{Theorem about antiderivative}\]
If both \( F(x) \) and \( G(x) \) are antiderivatives of \( f(x) \),
then there exists a constant \( C \) such that
\[ F(x) = G(x) + C \]
This theorem means that all antiderivatives of a function \( f(x) \) differ only by a constant.
To prove this theorem, we need to accept the following fact.
If \( f'(x) = 0 \), then \( f(x) = C \) (where \( C \) is an arbitrary constant).
\[ \text{Proof of the theorem about antiderivative}\]
Since both \( F(x) \) and \( G(x) \) are antiderivatives of \( f(x) \), by definition we have:
\[ F'(x) = f(x) \]
\[ G'(x) = f(x) \]
Now, let
\[ H(x) = F(x) - G(x) \]
Then,
\[ \begin{align}
H'(x) &= \left\{ F(x) - G(x) \right\} ' \\\\
&= F'(x) - G'(x) \\\\
&= f(x) - f(x) \\\\
&=0
\end{align} \]
Therefore, \( H(x) \) must be a constant function, so \( H(x) = C \) for some constant \( C \). That is,
\[ H(x) = C = F(x) - G(x) \]
Hence,
\[ F(x) = G(x) + C \]
holds.
From this theorem, it follows that all antiderivatives can be expressed in the form \( F(x) + C \),
where \( F(x) \) is a particular antiderivative and \( C \) is an arbitrary constant.
Therefore, we define this as the indefinite integral.
\[ \text{Indefinite integral}\]
Let \( F(x) \) be the antiderivative of the function \( f(x) \). In this case,
\[
F(x) + C \quad (C \text{ is an arbitrary constant})
\]
is called the indefinite integral of \( f(x) \) and is expressed as
\[
\int f(x) dx.
\]
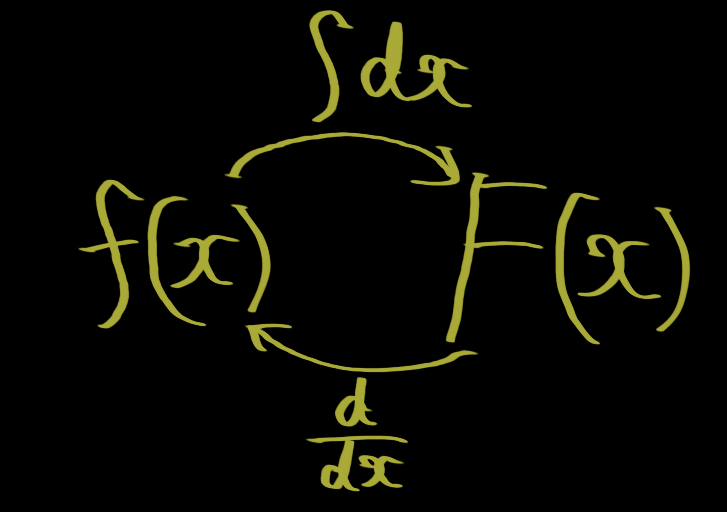
Additionally, \( C \) is specifically referred to as the constant of integration. The process of
finding the indefinite integral of a function \( f(x) \) is called integration.
Nayumi
If you look closely, the \( \int \) sign is quite stylish, like \( \int \int \).
Kaya
Yeah, it has a flowing shape and looks elegant. Anyway, getting back on topic, from the definition of
indefinite integrals, we can first understand the following.
\[ \left\{ \int f(x)dx \right\} ' = f(x) \]
\[ \int f'(x)dx = f(x) + C \]
The equation above means that differentiating an integrated function returns the original function,
and the equation below means that integrating a differentiated function results in the original function
plus an arbitrary constant.
These two equations express that indefinite integration is the inverse operation of differentiation.
Nayumi
So, using those two equations, you can create a loop between differentiation and integration.
Kaya
Exactly. Next, if we recall the rules for differentiating constant multiples, sums, and differences, we
can see that the following equations hold.
\[ \int cf(x)dx = c \int f(x)dx + C \ \ \left( c \ \text{is a constant} \right) \]
\[ \int \left\{ f(x) \pm g(x) \right\} dx = \int f(x)dx \pm \int g(x)dx + C \]
Nayumi
You're right, it has a similar form to those formulas.
Kaya
Exactly. Let's start by deriving the equation for a constant multiple.
\[ \begin{align}
c \int f(x)dx &= c \left\{ F(x) + C_1 \right\} \\\\
&= cF(x) + cC_1 \\\\
\end{align} \]
\[ \begin{align}
\int \left\{ cF(x) + cC_1 \right\} ' dx &= \int cF'(x) dx \\\\
&= \int cf(x) dx \\\\
&= c \int f(x)dx + C
\end{align}\]
Therefore,
\[ \int cf(x) dx = c \int f(x)dx + C \]
Kaya
Next, let's derive the equations for the sum and difference.
\[ \int f(x)dx \pm \int g(x)dx = \left\{ F(x) + C_1 \right\} \pm \left\{ G(x) + C_2 \right\} \]
\[ \begin{align}
\int \left\{ \left\{ F(x) + C_1 \right\} \pm \left\{ G(x) + C_2 \right\} \right\} ' dx &= \int \left\{
\left\{ F(x) + C_1 \right\} ' \pm \left\{ G(x) + C_2 \right\} ' \right\} dx \\\\
&= \int \left\{ F'(x) \pm G'(x) \right\} dx \\\\
&= \int \left\{ f(x) \pm g(x) \right\} dx \\\\
&= \int f(x)dx \pm \int g(x)dx + C
\end{align}\]
Therefore,
\[ \int \left\{ f(x) \pm g(x) \right\} dx = \int f(x)dx \pm \int g(x)dx + C \]
Nayumi
Are there any other general formulas for indefinite integrals?
Kaya
I'll introduce two more. The first one is the substitution rule.
\[ \text{Integration by substitution} \]
If \( x = g(u) \) is differentiable, then the following formula holds:
\[ \int f(x)dx = \int f(g(u))g'(u)du + C \]
Nayumi
Substitution means replacing the variable \( x \) with \( u \), right?
Kaya
That's right. Here's how the substitution rule for integration is derived.
Let \( x = g(u) \).
Differentiating both sides of
\[ \int f(x)dx = F(x) + C \]
with respect to \( u \), we get:
\[ \begin{align}
\frac{d}{du} \left\{ \int f(x)dx \right\} &= \frac{d}{du} F(x) + 0 \\\\
&= \frac{d}{dx} F(x) \frac{dx}{du} \\\\
&= f(x) \frac{dx}{du} \\\\
&= f(g(u))g'(u) \\\\
\end{align} \]
Therefore,
\[ \frac{d}{du} \left\{ \int f(x)dx \right\} = f(g(u))g'(u)\]
From the definition of the indefinite integral, we get:
\[ \int f(x)dx = \int f(g(u))g'(u)du + C \]
Rewriting this formula using
\[ x = g(u) \]
\[ g'(u) = \frac{dx}{du} ,\]
we get
\[ \int f(x)dx = \int f(x) \frac{dx}{du} du + C ,\]
which, formally, looks as if we’ve "canceled" the denominator of \( \frac{dx}{du} \).
Kaya
Alright, now let’s move on to the other general formula—integration by parts.
\[ \text{Integration by parts} \]
If both \( f(x) \) and \( g(x) \) are differentiable, then the following formula holds:
\[ \int f(x)g'(x)dx = f(x)g(x) - \int f'(x)g(x)dx + C \]
Nayumi
It looks kind of complicated.
Kaya
It may look tricky, but the derivation is surprisingly simple. We just use the product rule for
differentiation.
Using the product rule for differentiation,
\[ \left\{ f(x)g(x) \right\} ' = f'(x)g(x) + f(x)g'(x) \]
we move the term \( f'(x)g(x) \) to the other side and reverse both sides to get:
\[ f(x)g'(x) = \left\{ f(x)g(x) \right\} ' - f'(x)g(x) \]
Now, taking the indefinite integral of both sides:
\[ \begin{align}
\int f(x)g'(x)dx &= \int \left\{ f(x)g(x) \right\} ' dx - \int f'(x)g(x) dx \\\\
&= f(x)g(x) - \int f'(x)g(x) dx + C
\end{align} \]
Nayumi
It’s not as complicated as it looks.
Kaya
Right? That wraps up the general formulas for indefinite integrals. Now, let’s take a look at some
specific examples of indefinite integrals.
Indefinite integrals of various functions
Nayumi
Since indefinite integration is the reverse of differentiation, the indefinite integral of a function is
a function that, when differentiated, gives back the original function, right?
Kaya
Exactly. Last time we looked at the derivatives of various specific functions, so let’s keep those in
mind as we go through this.
Power functions
\[ \begin{align}
\ \ \ &\int x^{n} dx = \frac{1}{n+1} x^{n+1} + C \\\\
&( n \text{ is an integer except } -1, \ x \text{ is
a real number} )
\\\\
&\int \frac{1}{x} dx = \ln x + C \ \ ( x \rm \gt 0 ) \\\\
&\int x^{a} dx = \frac{1}{a+1} x^{a+1} + C \\\\
&( a \text{ is a real number except } -1, \ x \text{ is a
positive real number})
\end{align}\]
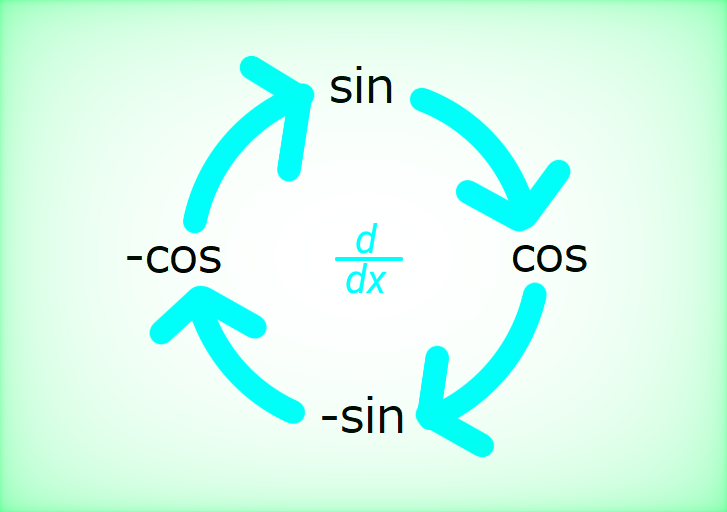
Trigonometric functions \[ \begin{align} &\int \sin x dx = - \cos x + C \quad (x \text{ is a real number})\\\\ &\int \cos x dx = \sin x + C \quad (x \text{ is a real number})\\\\ &\int \frac{1}{\cos ^2 x} dx = \tan x + C \\\\ & \quad (x \text{ is a real number except } \frac{(2n-1) \pi}{2}, \ n \text{ is an integer}) \end{align} \]
Exponential functions \[ \begin{align} &\int e^x dx = e^x + C \quad ( x \text{ is a real number} ) \\\\ &\int a^x dx = \frac{a^x}{\ln a} + C \\\\ & \quad ( x \text{ is a real number, } a \text{ is a positive real number except } 1 ) \end{align} \]
Trigonometric functions \[ \begin{align} &\int \sin x dx = - \cos x + C \quad (x \text{ is a real number})\\\\ &\int \cos x dx = \sin x + C \quad (x \text{ is a real number})\\\\ &\int \frac{1}{\cos ^2 x} dx = \tan x + C \\\\ & \quad (x \text{ is a real number except } \frac{(2n-1) \pi}{2}, \ n \text{ is an integer}) \end{align} \]
Exponential functions \[ \begin{align} &\int e^x dx = e^x + C \quad ( x \text{ is a real number} ) \\\\ &\int a^x dx = \frac{a^x}{\ln a} + C \\\\ & \quad ( x \text{ is a real number, } a \text{ is a positive real number except } 1 ) \end{align} \]
Nayumi
There sure are a lot of them.
Kaya
Yeah, but as long as you remember the differentiation rules we covered last time, you should be able to
understand them.
Nayumi
Proving all these formulas sounds like a lot of work…
Kaya
Not really. All you need to do is check that the derivative of the right-hand side gives back the
function being integrated on the left-hand side. We won’t go through all of them, but let’s verify the
first one—the integral of \( x^n \)—as an example.
\[ \left\{ \frac{1}{n+1} x^{n+1} + C \right\} ' = \frac{1}{n+1} (n+1)x^{(n+1)-1} = x^n \]
Nayumi
Hmmm, so that’s how you check it. That doesn’t sound too bad.
Kaya
Exactly. Try going through the rest when you have some time.
Nayumi
Got it!
References：
[1] James R. Newman, THE UNIVERSAL ENCYCLOPEDIA OF MATHEMATICS, George Allen & Unwin Ltd, 1964
[2] 石村園子, やさしく学べる微分積分, 共立出版, December 25, 1999
Previous
Ep. 7
Derivatives of
various functions
Derivatives of
various functions
Next
Ep. 9
Euler method
Euler method