TABLE OF CONTENTS
・Compound Interest Calculation
・The Trend of Ordinary Savings Interest Rates

Nayumi
Sigh… only 12 yen in interest… At this point, it’d be better if they didn’t even write it down.

Kaya
What’s wrong, Nayu-nee?

Nayumi
I saw the interest amount written in my bankbook—it was 12 yen. Just 12 yen. I can’t even buy a Chirole
chocolate with that.

Kaya
Well, bank interest rates are pretty low.

Nayumi
Way too low… My mom said there was a time when you could just put money in the bank and it would grow on
its own, but I can’t believe that…

Kaya
Yeah, back in the bubble era, that sort of thing did happen. But not anymore.

Nayumi
I hear people talk about the bubble a lot. What kind of trick made money grow so much back then?

Kaya
In that case, maybe I should explain compound interest.
Compound Interest Calculation

Nayumi
Compound interest… does that mean debt?

Kaya
Compound interest is used in calculating debt too, but in itself it’s just a method of calculating
interest, so it’s applied beyond debts. You could say bank interest is also calculated using compound
interest.

Nayumi
So it’s not just for debt. Then, what exactly is compound interest?

Kaya
If we think about the case of depositing money in a bank, it works like this.
\[ \text{Compound Interest Calculation}\]
Compound interest means including the interest in the principal used for calculating further
interest.
Example: Suppose you deposit ¥10,000 in a bank. If the annual interest rate is 1%, then after one year,
the interest you receive will be
\[ 10000 \times 0.01 = 100 \ \text{yen} \]
In compound interest, this ¥100 is added to the principal for calculating the next year’s interest. So,
after two years, the interest you receive will be
\[ (10000 + 100) \times 0.01 = 101 \ \text{yen} \]
In compound interest, the interest received in one year is added to the principal used for calculating the
interest of the following year.
The principal after \( n \) years can be calculated as follows:
Let the initial principal be \( P_0 \), and the interest rate be \( q \).
Then, the principal after 1 year, \( P_1 \), is
\[ P_1 = P_0 + qP_0 = P_0(1+q)\]
After 2 years, the principal \( P_2 \) is
\[ \begin{align}
P_2 &= P_1 + qP_1 \\\\
&= P_1(1+q) \\\\
&= P_0(1+q)(1+q) \\\\
&= P_0(1+q)^2
\end{align}\]
Continuing in this way, the principal after \( n \) years, \( P_n \), is
\[ P_n = P_0(1+q)^n\]
From the final formula, we can see that the principal is multiplied by \( (1+q) \) each year.
Furthermore, by rearranging this equation, we can determine the number of years it takes for the principal
to reach a specified amount.
\[ \begin{align}
P_n &= P_0(1+q)^n \\\\
\frac{P_n}{P_0} &= (1+q)^n \\\\
\ln \frac{P_n}{P_0} &= \ln (1+q)^n \\\\
\ln P_n - \ln P_0 &= n \ln (1+q) \\\\
n &= \frac{\ln P_n - \ln P_0}{\ln (1+q)}
\end{align}\]
By substituting the initial principal, target amount, and annual interest rate into this formula, we can
find the number of years required for the principal to reach the target amount.
For example, let’s calculate how long it would take ¥10,000 to grow to ¥1,000,000 at an annual interest rate
of 1%:
\[ \frac{\ln 1000000 - \ln 10000}{\ln (1+0.01)} = 462.8157851 \ldots \]

Nayumi
So it takes about 462 years? That’s hopeless…

Kaya
Unfortunately, that’s how it is. Using the logarithm laws, the numerator of this formula can be
rewritten as a fraction, so this result also means the number of years it takes to increase the
principal 100-fold at an annual interest rate of 1%.

Nayumi
Making it 100 times bigger is pretty tough, huh.

Kaya
Yeah. Well then, let’s take a look at the trend of Japan’s ordinary savings interest rates.
The Trend of Ordinary Savings Interest Rates

Nayumi
The interest rates used to be higher, right?

Kaya
Well, compared to now, they definitely were. Some parts of the data are missing, but I’ve made a graph
showing the trend of ordinary savings deposit interest rates.
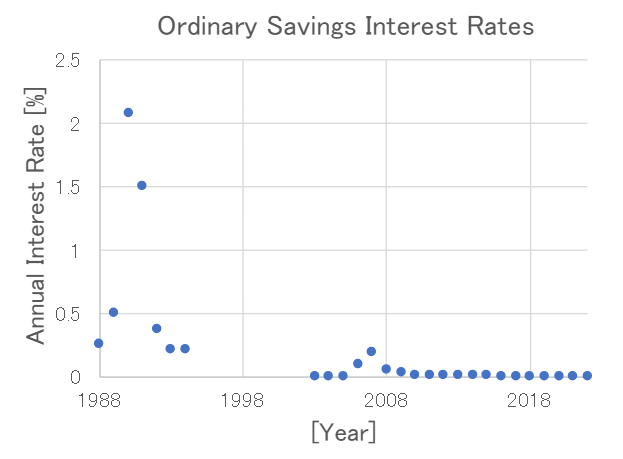
The data from 1988 to 1994 are taken from *“Bank Deposit Interest Rates (up to October 3, 1994)”*
(https://www.boj.or.jp/statistics/stop/depo_rate/cdab0860.csv).
The data from 2003 to 2022 are taken from the *Monthly Report of Recent Economic and Financial Developments*
(https://www.boj.or.jp/statistics/pub/sk/data/sk2.pdf).
For ordinary deposit interest rates, the values used are those at the end of each year.
The interest rate in 1990 is exceptionally high, as this year is known as the peak of the bubble economy.
The recession period from March 1991 to October 1993 is referred to as the bursting of the bubble.
Using the earlier formula to calculate the number of years it takes for the initial principal to increase by
1.5 times, based on ordinary savings interest rates from 1988 to 1994, we get the following results.
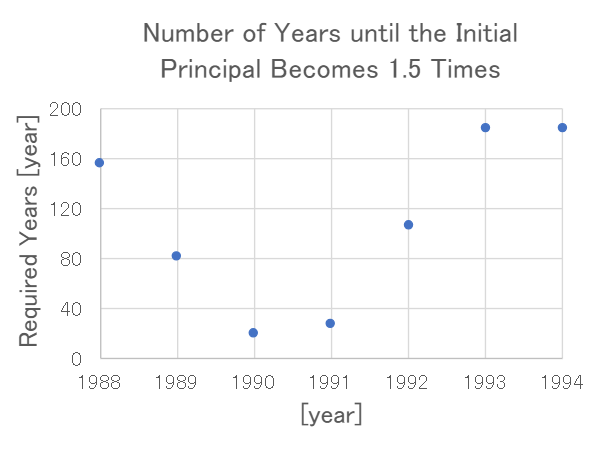
At the 1990 interest rate, it would take about 20 years for the principal to increase by 1.5 times.
With an interest rate like that, you can really feel your deposited money growing.
On the other hand, calculating with data from 2003 to 2022 gives the following results.
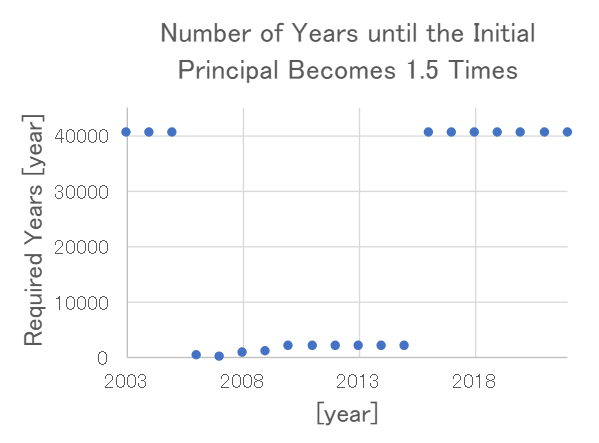

Nayumi
… This vertical axis isn’t wrong, right?

Kaya
It’s not wrong.

Nayumi
Forty thousand years? Unless you’re immortal, that’s impossible.

Kaya
Yeah. It just means we’re no longer in an era where money in an ordinary savings account actually grows.

Nayumi
Maybe I should invest instead?

Kaya
Well, investment carries more risk, but the returns are bigger. Still, without a decent amount of
starting capital, it doesn’t mean much either.

Nayumi
So at first, I just have to work hard and earn money the regular way.

Kaya
That’s about the life of an ordinary person.
References:
[1] Bank of Japan Home > Statistics > Discontinued Statistics / Revised Base Statistics > Deposits (through
October 3 1994), https://www.boj.or.jp/en/statistics/stop/depo_rate/index.htm, August 3, 2025
[2] 日本銀行HP 統計 統計書収録データ 金融経済統計月報, https://www.boj.or.jp/statistics/pub/sk/index.htm, August 11, 2023
[3] Wikipedia Lost Decades, https://en.wikipedia.org/wiki/Lost_Decades, August
3, 2025
[4] Wikipedia Economic bubble、https://en.wikipedia.org/wiki/Economic_bubble,
August 3, 2025
[5] James R. Newman, THE UNIVERSAL ENCYCLOPEDIA OF MATHEMATICS, George Allen & Unwin Ltd, 1964
Previous
Ep. 2
Radioactive Decay




