目次
・クーロンの法則
・宙に浮く磁石の運動方程式
・シミュレータ
ナユミ
カヤちゃん、この前テレビで磁石を宙に浮かす実験を見たんだけど、ああいうのも微分方程式で表せたりするの？
カヤ
実験条件にもよるだろうが、簡単なモデルでよければ解説するぞ。
ナユミ
お願いするわ。
クーロンの法則
磁石にはN極とS極があり、同じ極どうしは反発しあい、異なる極どうしは引き合います。
磁石が宙に浮いているのは同じ極どうしが反発しあっているからです。
この磁石間の相互作用を今回は単純なクーロンの法則で表します。
\[ クーロンの法則\]
\[ F_m = \frac{m _1 m_2}{4 \pi \mu _0 r^2} \]
\( F_m \) ：2つの磁石の間に働く力の大きさ、\( m_1 \) ：磁石1の磁荷、\( m_2 \) ：磁石2の磁荷、\( \pi \) ：円周率、\( \mu _0\) ：磁気定数、\( r \)
：2つの磁石の間の距離
磁荷はN極やS極が帯びている磁気の量のことです。
磁気定数はおよそ \( 1.26 \times 10^{-4} \) [kg・cm/s2/A2] という値を持つ定数です。
単位にあるAはアンペアと読み、これは電流の単位です。
クーロンの法則と万有引力の法則は式の形がとてもよく似ており、これらの法則は逆2乗則と呼ばれています。
クーロンの法則と万有引力の法則は式の形がとてもよく似ており、これらの法則は逆2乗則と呼ばれています。
宙に浮く磁石の運動方程式
落下する磁石が落下地点 \( \left( y = 0 \right) \) に設置した磁石から反発する力を受けていて、空気抵抗も働いているという状況を想定して運動方程式を立ててみます。
\[ 宙に浮く磁石の運動方程式\]
\[ m \frac{dv}{dt} = -mg + \frac{m _1 m_2}{4 \pi \mu _0 y^2} -pv -qv |v| \]
\( m \) ：落下する磁石の質量、\( v \) ：落下する磁石の速度、\( t \) ：時刻、\( g \) ：重力加速度、\( y \) ：落下する磁石の位置、\( p \) ：粘性抵抗の係数、\(
q \) ：慣性抵抗の係数
この微分方程式を解くことは難しく、グラフを書くには数値計算に頼ることになります。
ただ、落下する磁石には空気抵抗が働いているので、長い時間が経過すると磁石の速度は0に近づき、磁石は重力と磁力が釣り合う位置、つまり加速度が0となる位置で停止すると予想できます。
そこで、この磁石が最終的に留まる位置を先に求めておきます。
磁石が最終的に留まる位置では、
\[ \frac{dv}{dt} = 0\]
\[ v = 0\]
だから、
\[ \begin{align}
0 &= -mg + \frac{m _1 m_2}{4 \pi \mu _0 y^2} \\\\
mg &= \frac{m _1 m_2}{4 \pi \mu _0 y^2} \\\\
mgy^2 &= \frac{m _1 m_2}{4 \pi \mu _0} \\\\
y^2 &= \frac{m _1 m_2}{4 \pi \mu _0 mg} \\\\
y &= \sqrt{\frac{m _1 m_2}{4 \pi \mu _0 mg}}
\end{align}\]
また、先ほどの運動方程式ですが、次のように変形しておくとすっきりします。
\[ \begin{align}
m \frac{dv}{dt} &= -mg + \frac{m _1 m_2}{4 \pi \mu _0 y^2} -pv -qv |v| \\\\
\frac{dv}{dt} &= -g + \frac{k}{4 \pi \mu _0 y^2} - \alpha v - \beta v |v| \\\\
\end{align}\]
ここで、
\[ k = \frac{m _1 m_2}{m}\]
\[ \alpha = \frac{p}{m}\]
\[ \beta = \frac{q}{m}\]
とおいた。
ナユミ
ふむ、\( g \) 、\( \pi \) 、\( \mu _0 \) は全部定数だから、この運動方程式の解は \( k \) 、\( \alpha \) 、\( \beta \) に左右されるのね。
カヤ
そういうことだな。それじゃあ、この運動方程式を数値計算した結果を見ていきたいんだが、その前にこの現象のシミュレータを作ったから少し遊んでみてくれ。
シミュレータ
t: 0s
y: 4cm
シミュレータの使い方
[1] パラメータ \( k \) 、\( \alpha \) 、\( \beta \) の値を入力します。
[2] 朱色の磁石をドラッグ&ドロップして磁石を落とす位置を決めます。スマホやタブレットで閲覧している方など、ドラッグ&ドロップができない場合は朱色の▲▼ボタンで磁石を移動してください。
[3] 「開始/停止」ボタンを押してシミュレーション開始。
[4] 途中で止めたい場合はもう一度「開始/停止」ボタンを押します。さらにもう一度ボタンを押すと同じ場所から再開できます。
[5] ブラウザの調子によっては動きが遅くなることがありますが、そのときは一度「開始/停止」ボタンを押してからもう一度ボタンを押すと動きが元に戻ることがあります。
[6] パラメータの値を変えて再びシミュレーションをする場合は、ブラウザの再読み込みをしてください。
[1] パラメータ \( k \) 、\( \alpha \) 、\( \beta \) の値を入力します。
[2] 朱色の磁石をドラッグ&ドロップして磁石を落とす位置を決めます。スマホやタブレットで閲覧している方など、ドラッグ&ドロップができない場合は朱色の▲▼ボタンで磁石を移動してください。
[3] 「開始/停止」ボタンを押してシミュレーション開始。
[4] 途中で止めたい場合はもう一度「開始/停止」ボタンを押します。さらにもう一度ボタンを押すと同じ場所から再開できます。
[5] ブラウザの調子によっては動きが遅くなることがありますが、そのときは一度「開始/停止」ボタンを押してからもう一度ボタンを押すと動きが元に戻ることがあります。
[6] パラメータの値を変えて再びシミュレーションをする場合は、ブラウザの再読み込みをしてください。
ナユミ
\( \alpha \) と \( \beta \) の値を大きくすると、磁石の振れ幅がすぐに小さくなるわね。
カヤ
空気抵抗が大きくなるからな。\( \alpha \) の値のみを変化させて比較してみたグラフはこれだな。
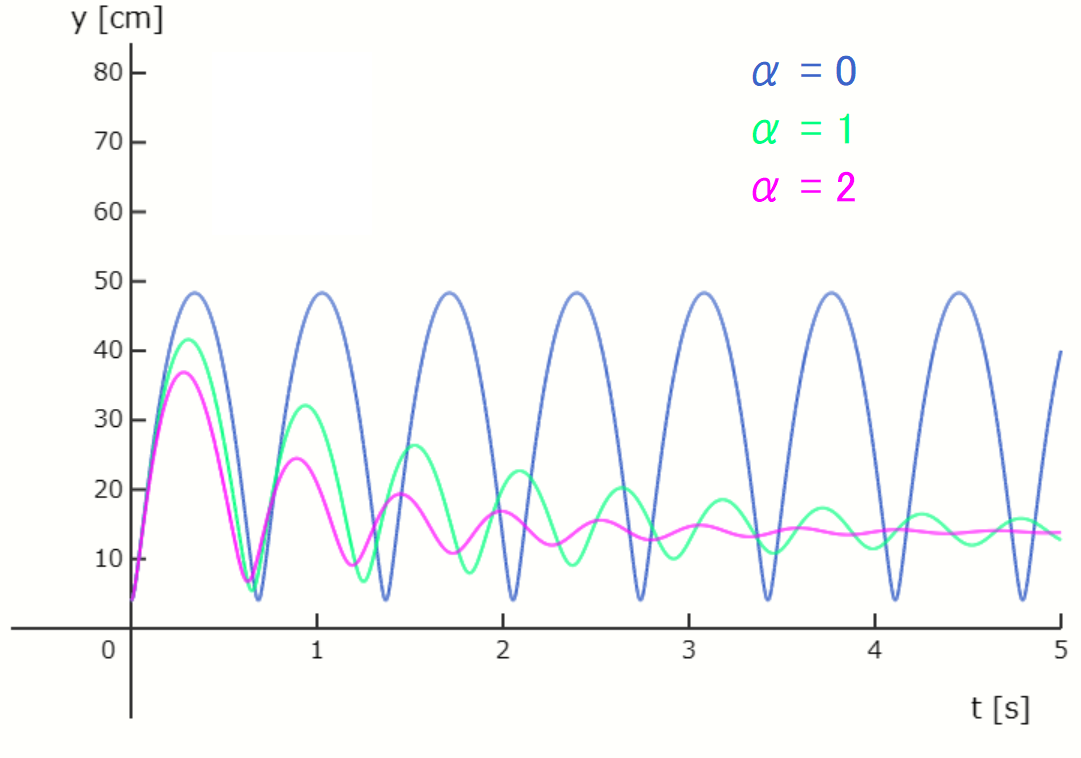
\( k = 300\) 、\( \beta = 0\) 、\( y_0 = 4 \) として、\( \alpha \) を0、1、2の計3種類の条件で数値計算。
数値計算には4次のルンゲ=クッタ法を用いた。
磁石が最終的に落ち着く位置は先ほどの式で計算すると、 \[ \begin{align} y &= \sqrt{\frac{m _1 m_2}{4 \pi \mu _0 mg}} \\\\ &= \sqrt{\frac{k}{4 \pi \mu _0 g}} \\\\ &= \sqrt{\frac{300}{4 \pi \times 1.26 \times 10^{-4} \times 980}} \\\\ &= 13.90 \ldots \end{align}\]
磁石が最終的に落ち着く位置は先ほどの式で計算すると、 \[ \begin{align} y &= \sqrt{\frac{m _1 m_2}{4 \pi \mu _0 mg}} \\\\ &= \sqrt{\frac{k}{4 \pi \mu _0 g}} \\\\ &= \sqrt{\frac{300}{4 \pi \times 1.26 \times 10^{-4} \times 980}} \\\\ &= 13.90 \ldots \end{align}\]
ナユミ
\( \beta \) の値を変化させるとどうなるかな？
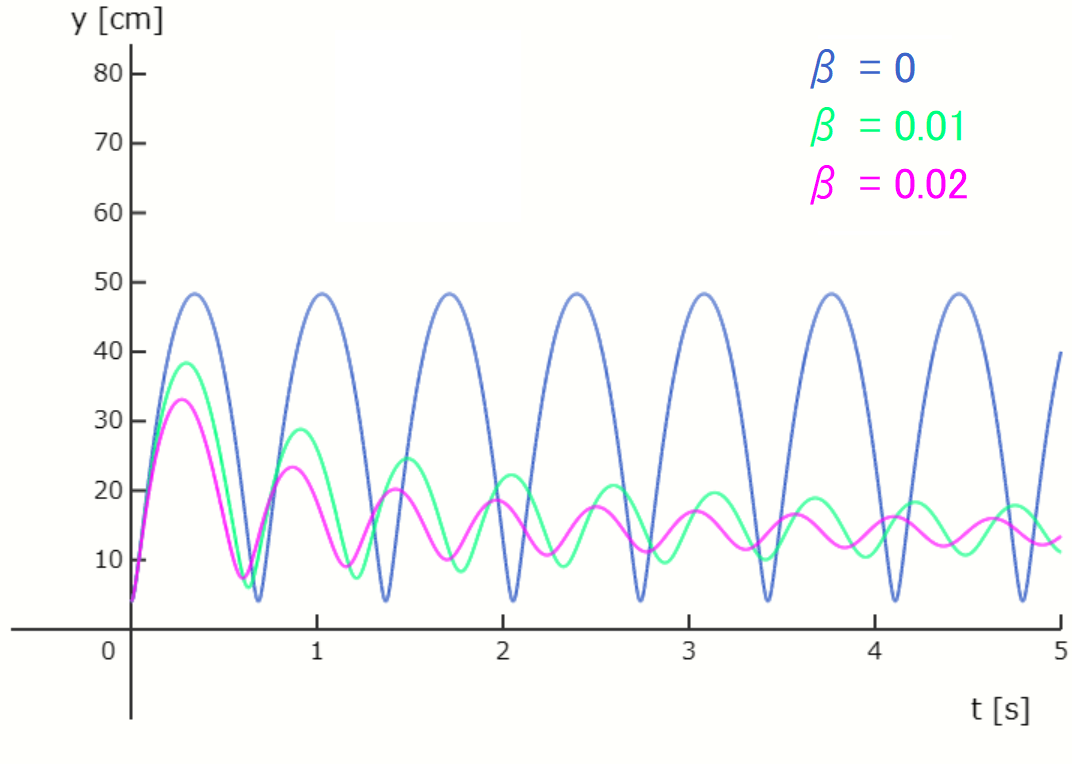
\( k = 300\) 、\( \alpha = 0\) 、\( y_0 = 4 \) として、\( \beta \) を0、0.01、0.02の計3種類の条件で数値計算。
数値計算には4次のルンゲ=クッタ法を用いた。
\( \beta \) は速度の2乗に比例する慣性抵抗の係数です。 そのため、磁石の速度の絶対値が1より大きいうちは慣性抵抗は粘性抵抗の係数である \( \alpha \) よりも振れ幅に大きく影響します。 一方、磁石の速度の絶対値が1より小さくなると、慣性抵抗は粘性抵抗よりも振れ幅に影響しにくくなるため、慣性抵抗のみが働く場合、振れ幅が小さくなってからも長い時間振れ続けるという特徴があります。
\( \beta \) は速度の2乗に比例する慣性抵抗の係数です。 そのため、磁石の速度の絶対値が1より大きいうちは慣性抵抗は粘性抵抗の係数である \( \alpha \) よりも振れ幅に大きく影響します。 一方、磁石の速度の絶対値が1より小さくなると、慣性抵抗は粘性抵抗よりも振れ幅に影響しにくくなるため、慣性抵抗のみが働く場合、振れ幅が小さくなってからも長い時間振れ続けるという特徴があります。
ナユミ
それにしても、テレビで見た磁石はこんなに振れてなかった気がするけど？
カヤ
まあ上のグラフの例は空気抵抗の係数が小さいからな。
それと、実際の実験をするときは磁石の周りのものとの摩擦力も影響するから、このグラフのようには見えないだろうな。
ナユミ
そういうことね。
参考：
[1] Wikipedia クーロンの法則、https://ja.wikipedia.org/wiki/クーロンの法則、2023年10月14日閲覧
[2] Wikipedia 磁荷、https://ja.wikipedia.org/wiki/磁荷、2023年10月14日閲覧
[3] Wikipedia 逆2乗の法則、https://ja.wikipedia.org/wiki/逆2乗の法則、2023年10月14日閲覧
前の記事
第11話
空気抵抗が
あるときの運動
空気抵抗が
あるときの運動
次の記事
第13話
賭け事で破産する確率
賭け事で破産する確率