目次
・2体問題
・物体の衝突の表現
・計算例
カヤ
よっ、ほい、あーまたミスっちまった。
ナユミ
何やってるの、カヤちゃん？
カヤ
2体問題を枠の中でやってみたら面白いかなと思ってな。やってみたらこれそのまま弾避けゲームになるなって思って作ってみたんだ。
ナユミ
へえ、私もやってみていいかしら？
t: 0
―説明書―
このゲームには3つのモードがあります。 モードは右側の一番下のセレクトボックスから選択できます。
モードの種類
[1] 観察
赤玉と青玉の動きを観察するモードです。
[2] ゲーム（ユーザー指定）
ユーザーが指定したパラメータに基づいて動く赤玉と青玉を避けるゲームです。 制限時間と残機の設定はなく、ゲーム画面の上側に被弾回数が表示されます。
[3] ゲーム（3連戦）
動く赤玉と青玉を30秒間避け続けるゲームです。 ステージは3面構成で、各ステージで3回被弾するとGameOverです。 ゲーム画面の上側に残機数が表示されます。
モード[1]と[2]では、画面下の矢印ボタンで赤玉と青玉の初期位置を変更できます。 「青」ボタンを押すと「赤」ボタンに切り替わり、動かせる玉が青玉から赤玉に変わります。 同様に、「赤」ボタンを押すと、「青」ボタンになり、動かせる玉が青玉から赤玉に変わります。
画面右のインプットボックスから玉の質量、x軸方向の初期速度、y軸方向の初期速度をそれぞれ変更できます。 各パラメータの添え字番号1が青玉、番号2が赤玉です。
「開始/停止」ボタンを押すと赤玉と青玉が動き始めます。モード[2]と[3]では矢印ボタンを押して黄色の玉（自機）を動かせます。
右側の「効果音」セレクトボックスから、効果音の有無を切り替えられます。 また、PCで閲覧している方は矢印ボタンの下にある「キーボードOff」のボタンを押すと「キーボードOn」に切り替わり、矢印ボタンの代わりにキーボードの矢印キーでも操作できるようになります。 「キーボードOn」の状態ではブラウザを矢印キーでスクロールできなくなります。元に戻したい場合は、「キーボードOn」ボタンを押して「キーボードOff」に戻してください。
このゲームには3つのモードがあります。 モードは右側の一番下のセレクトボックスから選択できます。
モードの種類
[1] 観察
赤玉と青玉の動きを観察するモードです。
[2] ゲーム（ユーザー指定）
ユーザーが指定したパラメータに基づいて動く赤玉と青玉を避けるゲームです。 制限時間と残機の設定はなく、ゲーム画面の上側に被弾回数が表示されます。
[3] ゲーム（3連戦）
動く赤玉と青玉を30秒間避け続けるゲームです。 ステージは3面構成で、各ステージで3回被弾するとGameOverです。 ゲーム画面の上側に残機数が表示されます。
モード[1]と[2]では、画面下の矢印ボタンで赤玉と青玉の初期位置を変更できます。 「青」ボタンを押すと「赤」ボタンに切り替わり、動かせる玉が青玉から赤玉に変わります。 同様に、「赤」ボタンを押すと、「青」ボタンになり、動かせる玉が青玉から赤玉に変わります。
画面右のインプットボックスから玉の質量、x軸方向の初期速度、y軸方向の初期速度をそれぞれ変更できます。 各パラメータの添え字番号1が青玉、番号2が赤玉です。
「開始/停止」ボタンを押すと赤玉と青玉が動き始めます。モード[2]と[3]では矢印ボタンを押して黄色の玉（自機）を動かせます。
右側の「効果音」セレクトボックスから、効果音の有無を切り替えられます。 また、PCで閲覧している方は矢印ボタンの下にある「キーボードOff」のボタンを押すと「キーボードOn」に切り替わり、矢印ボタンの代わりにキーボードの矢印キーでも操作できるようになります。 「キーボードOn」の状態ではブラウザを矢印キーでスクロールできなくなります。元に戻したい場合は、「キーボードOn」ボタンを押して「キーボードOff」に戻してください。
ナユミ
結構難しいわね、これ。赤玉と青玉の動きがなかなかに複雑よ。
カヤ
だろう。玉の初期位置や初期速度、質量に応じて動きがコロコロ変わるから、何度でも遊べるんだな。
ナユミ
そうね。ところで、このゲームに使った「2体問題」っていうのは何なのかしら？
カヤ
そうだな。じゃあ2体問題について解説しておこう。
2体問題
2体問題は互いに相互作用を及ぼす2つの物体の運動についての問題です。
身近な例としては、地球の周りを回る月の運動などがあります。
物体の運動を2次元平面上に限定し、相互作用として万有引力を考えると、この問題は次の4つの微分方程式により表されます。
\[ 2体問題\]
\[ \begin{align}
\frac{d v_{x1}}{dt} &= \frac{Gm_2}{r^2} \cdot \frac{x_2 - x_1}{r} \\\\
\frac{d v_{x2}}{dt} &= \frac{Gm_1}{r^2} \cdot \frac{x_1 - x_2}{r} \\\\
\frac{d v_{y1}}{dt} &= \frac{Gm_2}{r^2} \cdot \frac{y_2 - y_1}{r} \\\\
\frac{d v_{y2}}{dt} &= \frac{Gm_1}{r^2} \cdot \frac{y_1 - y_2}{r} \\\\
\end{align}\]
ただし、
\[ r = \sqrt{ \left( x_2 - x_1 \right) ^2 + \left( y_2 - y_1 \right) ^2 }\]
\( m_1 \) ：物体1の質量、\( m_2 \) ：物体2の質量、
\( x_1 \) ：物体1のx座標、 \( x_2 \) ：物体2のx座標、
\( y_1 \) ：物体1のy座標、\( y_2 \) ：物体2のy座標、
\( v_{x1} \) ：物体1の速度のx成分、\( v_{x2} \) ：物体2の速度のx成分、
\( v_{y1} \) ：物体1の速度のy成分、\( v_{y2} \) ：物体2の速度のy成分、
\( r \) ：物体1と物体2の間の距離、\( G \) ：万有引力定数、
\( t \) ：時刻
\( x_1 \) ：物体1のx座標、 \( x_2 \) ：物体2のx座標、
\( y_1 \) ：物体1のy座標、\( y_2 \) ：物体2のy座標、
\( v_{x1} \) ：物体1の速度のx成分、\( v_{x2} \) ：物体2の速度のx成分、
\( v_{y1} \) ：物体1の速度のy成分、\( v_{y2} \) ：物体2の速度のy成分、
\( r \) ：物体1と物体2の間の距離、\( G \) ：万有引力定数、
\( t \) ：時刻
ナユミ
ふーん、この4つの微分方程式をルンゲ=クッタ法とかを使って解いてるのね。けど、玉が壁にぶつかったり、玉同士がぶつかったりしたときもこの式で表せるの？
カヤ
いや、ぶつかったときの表現についてはまた別の式を使っているんだ。
物体の衝突の表現
玉が壁に衝突したときには衝突方向の速度成分の符号を反転させています。
例えば、青玉が上の壁に衝突した場合、\( v_{y1} \) を \( - v_{y1} \) へと置き換えるといった具合です。
玉同士が衝突した場合は、次式で衝突後の速度 \( V_{x1} \) 、\( V_{x2} \) 、\( V_{y1} \) 、\( V_{y2} \) をそれぞれ計算しています。 この式は、x軸方向、y軸方向それぞれで完全弾性衝突を仮定して導かれています。
玉同士が衝突した場合は、次式で衝突後の速度 \( V_{x1} \) 、\( V_{x2} \) 、\( V_{y1} \) 、\( V_{y2} \) をそれぞれ計算しています。 この式は、x軸方向、y軸方向それぞれで完全弾性衝突を仮定して導かれています。
\[ \begin{align}
V_{x1} &= \frac{m_1 - m_2}{m_1 + m_2} \cdot v_{x1} + \frac{2 m_2}{m_1 + m_2} \cdot v_{x2} \\\\
V_{x2} &= \frac{2 m_1}{m_1 + m_2} \cdot v_{x1} + \frac{m_2 - m_1}{m_1 + m_2} \cdot v_{x2} \\\\
V_{y1} &= \frac{m_1 - m_2}{m_1 + m_2} \cdot v_{y1} + \frac{2 m_2}{m_1 + m_2} \cdot v_{y2} \\\\
V_{y2} &= \frac{2 m_1}{m_1 + m_2} \cdot v_{y1} + \frac{m_2 - m_1}{m_1 + m_2} \cdot v_{y2}
\end{align}\]
ナユミ
2体問題の微分方程式とこの衝突の計算式の組み合わせで、あの複雑な玉の動きが計算されているのね。
カヤ
そういうことだな。最後に具体的な計算例を2つ見てみよう。
計算例
跳ね回る玉の動きは複雑ですが、パラメータの値によっては比較的簡単な動きになることもあります。
例えば、
\[ m_1 = m_2 = 10^8 \]
\[ x_1 = -100 = -x_2 \]
\[ y_1 = 0 = -y_2 \]
\[ v_{x1} = -500 = -v_{x2} \]
\[ v_{y1} = -500 = -v_{y2} \]
という初期条件で計算を開始した結果を、
横軸に \( t \) 、縦軸に \( x_1 \) 、\( x_2 \) 、\( y_1 \) 、\( y_2 \) をそれぞれ取ってグラフにしたものが下図です。
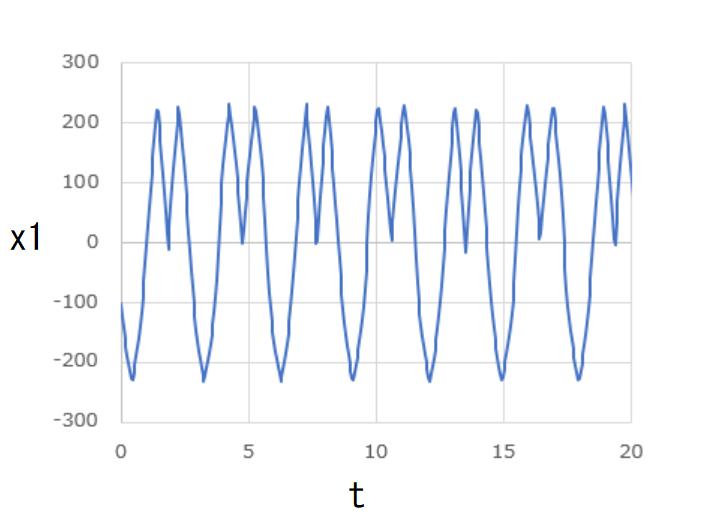
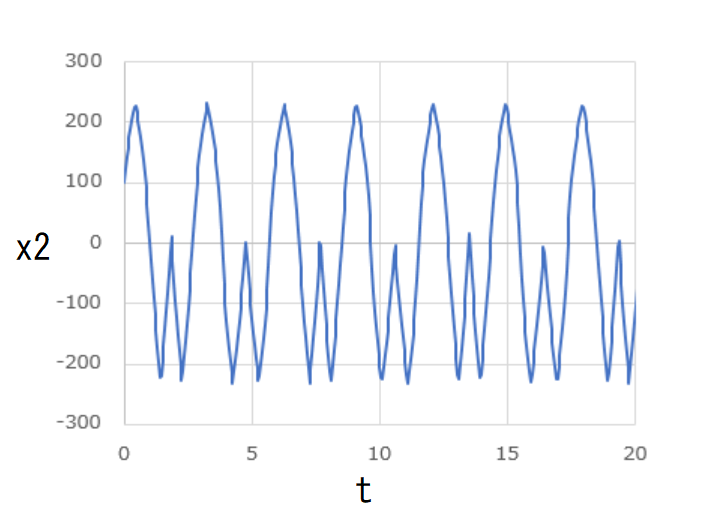
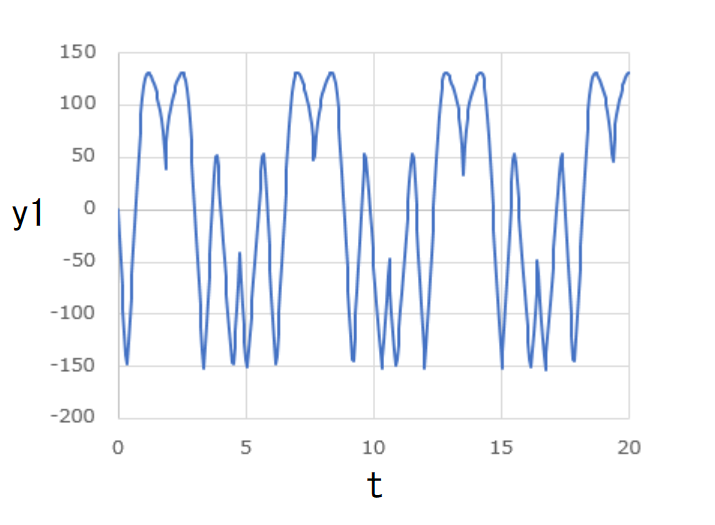
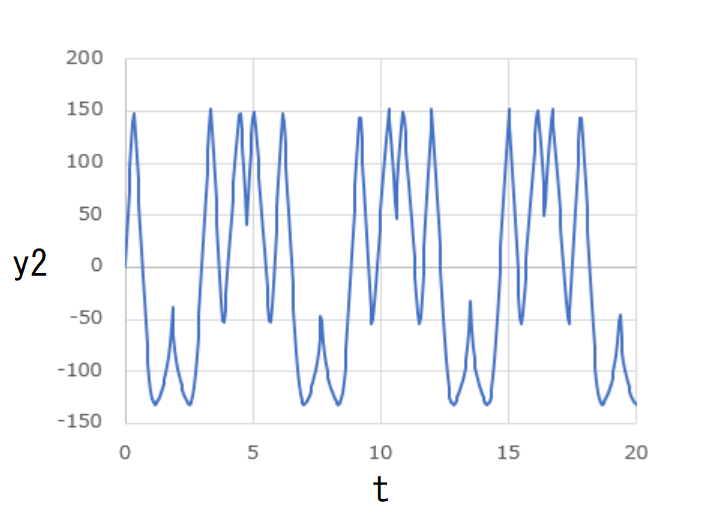
これらのグラフはいずれも周期的な変動を見せています。
また、任意の時刻において、
\[ x_1 = -x_2\]
\[ y_1 = -y_2\]
が成り立っています。
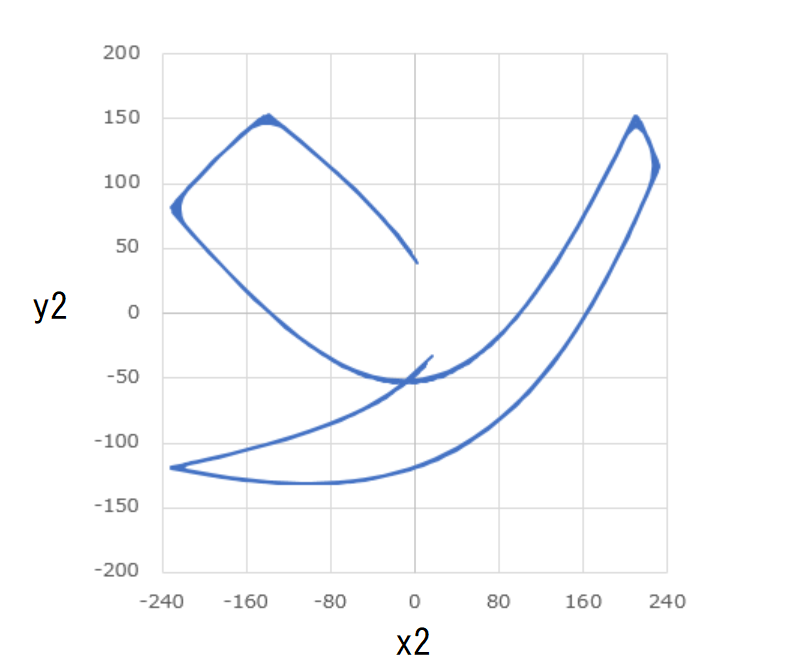
玉1と玉2の軌道をxy平面上に図示すると次のようになります。
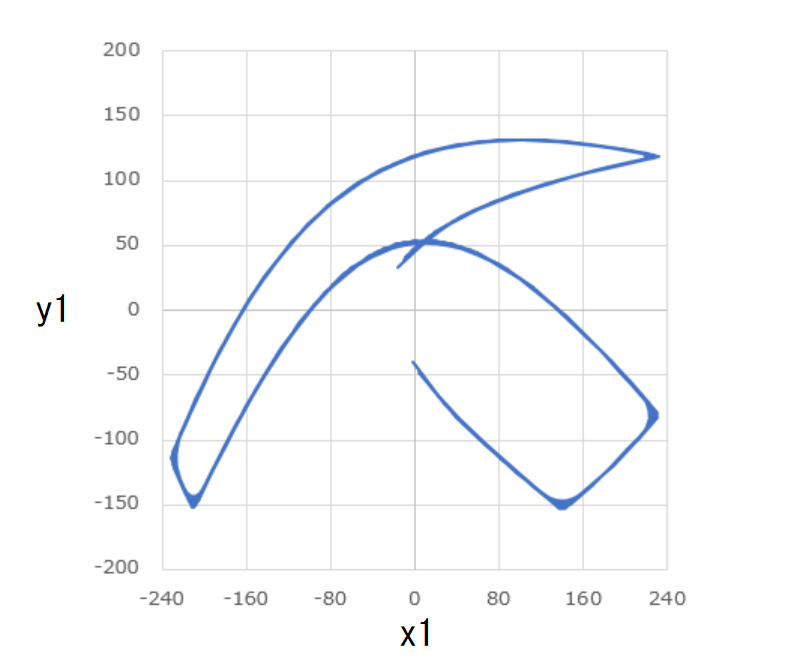
どちらの玉も一定の軌道を往復していることがわかります。
この計算条件のように、周期的で解析が容易な軌道もありますが、一般にはそうはなりません。
もう一つの具体例として、
\[ m_1 = m_2 = 10^8 \]
\[ x_1 = -150, \ x_2 = 100 \]
\[ y_1 = -120, \ y_2 = 0 \]
\[ v_{x1} = -300, \ v_{x2} = 200\]
\[ v_{y1} = -500 = -v_{y2} \]
という初期条件で計算を開始した結果を先ほど同様にグラフにしてみました。
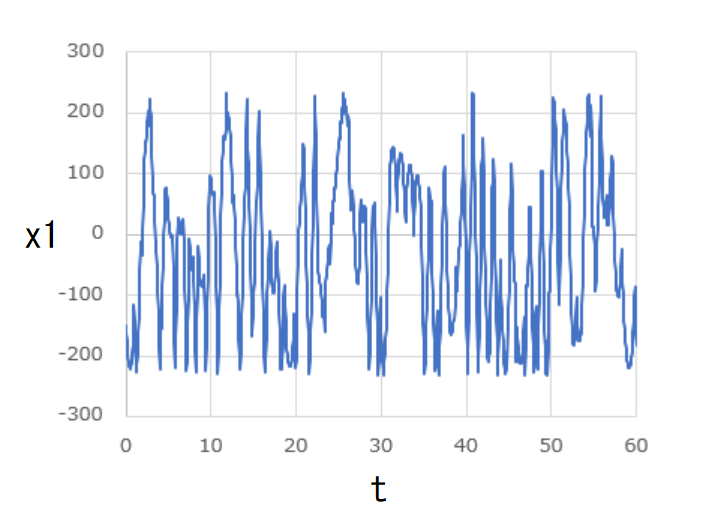
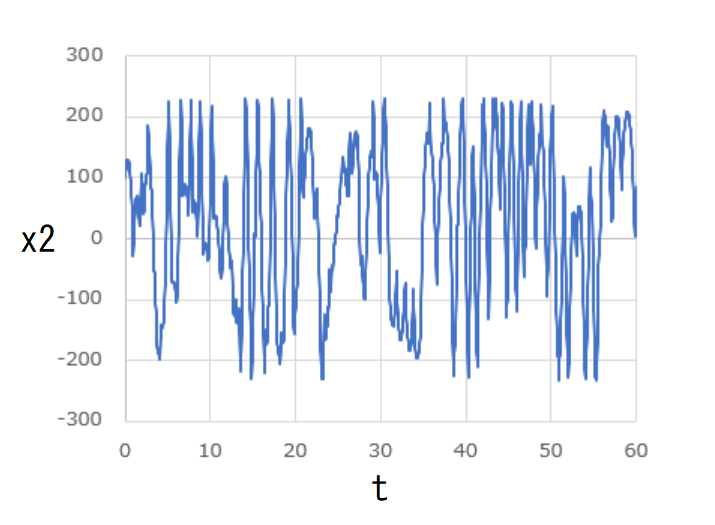
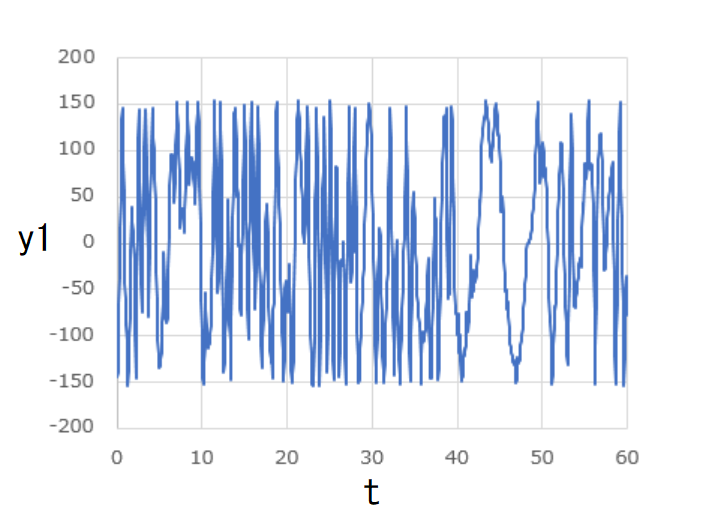
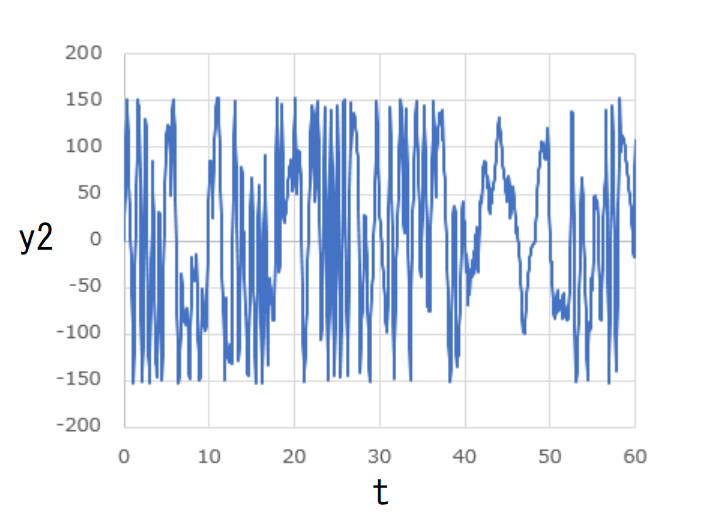
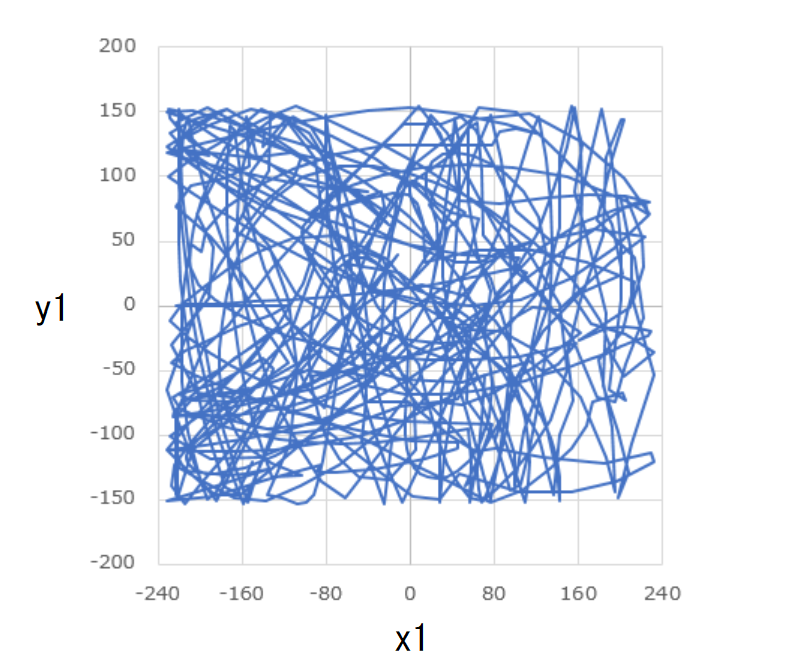
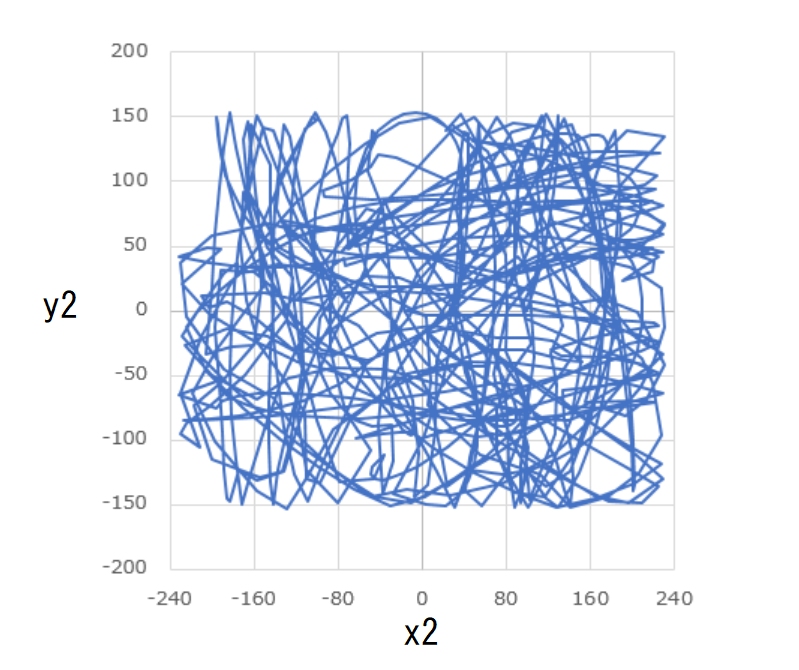
先ほどとは異なり、いずれも非周期的な変動を見せています。
軌道も複雑で、どちらの玉も枠の中一体を飛び回っていることがわかります。
ナユミ
本当、ちょっとした条件の違いでずいぶん様子が違うのね。
カヤ
一般にどういった動きをするのかの予測は難しいだろうな。まあ色々と試してみてくれよな。
参考：
[1] 参考：ニュートン力学における万有引力の2体問題、https://home.hirosaki-u.ac.jp/relativity/重力場中のテスト粒子の運動/万有引力の2体問題/、2023年12月25日閲覧
[2] Wikipedia 弾性衝突、https://ja.wikipedia.org/wiki/弾性衝突、2023年12月25日閲覧
前の記事
第14話
コッホ雪片
コッホ雪片
次の記事
第16話
2次元のランダムウォークと拡散方程式
2次元のランダムウォークと拡散方程式