複利計算

　　・複利計算

　　・普通預金金利の推移

この記事を読む助けになる数学の記事
・数値計算：1話、 2話、 5話

ナユミ

はあ…、お利息は12円かあ…。これなら書いてないほうがいいぐらいよ。

カヤ

どうしたんだ？ナユ姉。

ナユミ

通帳に利息の金額が書いてあったんだけど、12円なのよ、12円。これじゃあチロルチョコも買えないわよ。

カヤ

まあ、銀行の金利は低いからなあ。

ナユミ

低すぎるわよ…。お母さんは昔は銀行にお金預けておけば勝手に増えてた時代もあったなんて言ってたけど、信じられないわ…。

カヤ

そうだなあ、バブルの頃だったらそういうことにもなってたんだろうけどな。今じゃあ全然ダメだな。

ナユミ

バブルってよく聞くわよね。いったいどういうカラクリでお金がそんなに増えてたのかしら？

カヤ

そういうことなら、複利の話でもしてみようか。

複利計算

ナユミ

複利って、借金のこと？

カヤ

複利は借金の計算にも使われるが、複利自体は利息（利子）の計算方法で借金以外でも使われるぞ。銀行の利息も複利で計算しているといえる。

ナユミ

借金だけじゃなかったのね。それで、複利はどういうものなの？

カヤ

銀行にお金を預ける場合を想定すると、こういうものだな。

\[ 複利計算\] 　複利とは、利息の計算に用いる元金に利息を含めることである。

例：はじめに、銀行に1万円を預けたとする。銀行の年利率が1%であるとしたら、1年後に受け取る利息は \[ 10000 \times 0.01 = 100 \ (\rm 円)\] となる。複利ではこの利息100円を次の年の利息の計算に用いる元金に含めるので、2年後に受け取る利息は \[ (10000 + 100) \times 0.01 = 101 \ (\rm 円)\] となる。以後同様。

　ある年にもらえる利息を、次の年にもらえる利息の計算に使う元金に加えるのが複利の計算方法です。 \( n \) 年後の元金は次のように計算できます。

　はじめの元金を \( P_0 \) 、利息を \( q \) とする。このとき、1年後の元金 \( P_1 \) は、 \[ P_1 = P_0 + qP_0 = P_0(1+q)\] となる。2年後の元金 \( P_2 \) は、 \[ \begin{align} P_2 &= P_1 + qP_1 \\\\ &= P_1(1+q) \\\\ &= P_0(1+q)(1+q) \\\\ &= P_0(1+q)^2 \end{align}\] となる。以下同様と考えると、\( n \) 年後の元金 \( P_n \) は、 \[ P_n = P_0(1+q)^n\] となる。

最後の式から、元金は毎年 \( (1+q) \) 倍されていることがわかります。また、この式を次のように変形すると、指定した金額に元金が到達する年数を求めることができます。

\[ \begin{align} P_n &= P_0(1+q)^n \\\\ \frac{P_n}{P_0} &= (1+q)^n \\\\ \ln \frac{P_n}{P_0} &= \ln (1+q)^n \\\\ \ln P_n - \ln P_0 &= n \ln (1+q) \\\\ n &= \frac{\ln P_n - \ln P_0}{\ln (1+q)} \end{align}\]

この式に、はじめの元金、到達金額、年利率を入れると、到達金額となる年数が求められます。例えば、1万円が年利率1%で100万円になるまでを計算してみると次のようになります。

\[ \frac{\ln 1000000 - \ln 10000}{\ln (1+0.01)} = 462.8157851 \ldots \]

ナユミ

だいたい462年ってこと？全然駄目じゃない…

カヤ

残念ながらこんなものだな。この式の分子は対数法則を使えば分数に戻せるから、この結果は年利率1%で元金を100倍にするのにかかる年数とも言える。

ナユミ

100倍にするのは大変なのね。

カヤ

そうだな。それじゃあ最後に日本の普通預金金利の推移を見てみよう。

普通預金金利の推移

ナユミ

昔の金利は高かったのよね？

カヤ

まあ今と比べたら高かったよな。途中データが抜けている部分があるが、普通預金金利の推移をグラフにしてみたぞ。

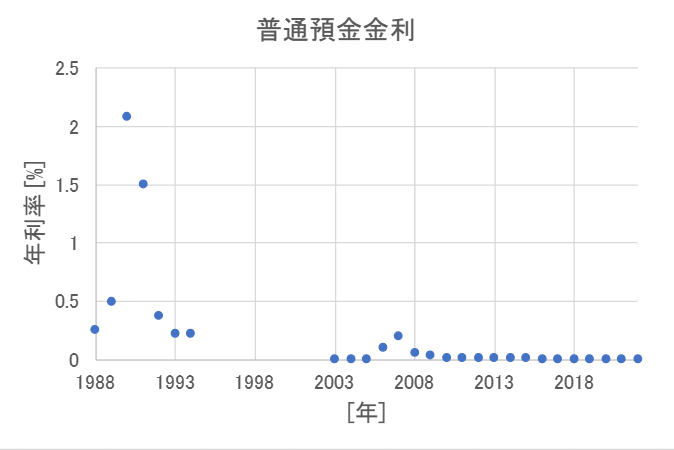
1988年-1994年のデータは「銀行預金金利（1994年10月3日まで）」（https://www.boj.or.jp/statistics/stop/depo_rate/cdab0860.csv）を参照。
2003年-2022年のデータは「金融経済統計月報」（https://www.boj.or.jp/statistics/pub/sk/data/sk2.pdf）を参照。
普通預金金利の値はいずれも年末時点のものを参照。

　1990年の値がずば抜けて高いですが、この年はバブル絶頂期と呼ばれています。そして、1991年の3月から1993年の10月までの景気後退期はバブル崩壊と呼ばれています。はじめの元金が1.5倍になるまでの年数を先の式を使って1988年-1994年の普通預金金利から求めると次のようになります。

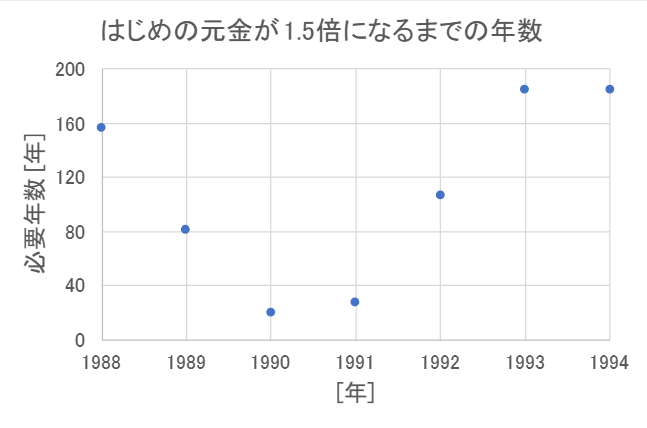
1990年の金利なら20年ぐらいで1.5倍になる計算になります。このくらいの金利だと、預けたお金が増えていくという実感もあると思います。一方、2003年-2022年のデータで計算すると次のようになります。

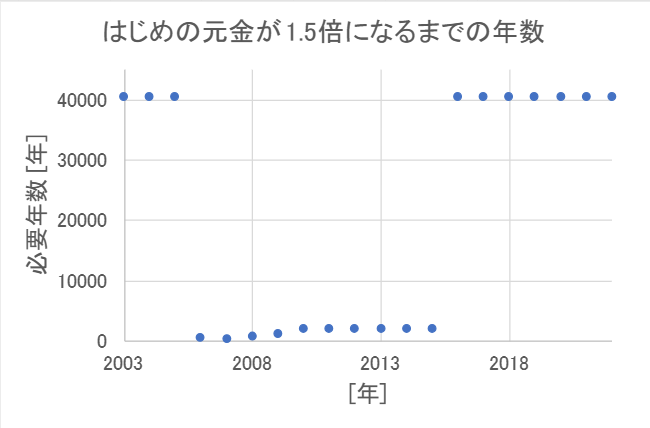
ナユミ

…、これ縦軸間違ってないよね？

カヤ

間違ってないぞ。

ナユミ

4万年って、不老不死にでもならないと無理じゃないの。

カヤ

まあな。普通預金にお金を預けてお金が増える時代じゃないってことだな。

ナユミ

投資でもしたほうがいいのかしら？

カヤ

まあ投資の方がリスクはあるものの、利回りは大きいよな。けど、いずれにしてもある程度のまとまった元金を用意できないと、あまり意味はないけどな。

ナユミ

はじめはまじめに働くしかないのね。

カヤ

庶民生活はそんなところだな。

参考：
[1] 日本銀行HP 統計更新停止／旧基準統計など銀行預金金利（1994年10月 3日まで）、https://www.boj.or.jp/statistics/stop/depo_rate/index.htm、2023年8月11日閲覧
[2] 日本銀行HP 統計統計書収録データ金融経済統計月報、https://www.boj.or.jp/statistics/pub/sk/index.htm、2023年8月11日閲覧
[3] Wikipedia バブル崩壊、https://ja.wikipedia.org/wiki/バブル崩壊、2023年8月11日閲覧
[4] Wikipedia Economic bubble、https://en.wikipedia.org/wiki/Economic_bubble、2023年8月11日閲覧
[5] George Allen & Unwin Ltd 著、矢野健太郎　訳補、ブルーバックス　現代数学百科、講談社、1968年11月30日発行

第2話
放射性原子の崩壊

第4話
カビの増殖